机器学习2—分类算法之决策树(Decision Tree)
决策树 (Decision Tree)
- 前言
-
-
- 1.分类模型实例讲解
- 2.常见的分类算法
-
- 一、决策树的基本概念
- 二、DTC算法
- 三、用决策树来分析鸢尾花
-
-
- 3.1数据集
- 3.2决策树分析鸢尾花
-
- 四、数据集划分和分类评估
- 五、区域划分对比
- 六、使用pydotplus可视化决策树
- 总结
前言
1.分类模型实例讲解
分类算法的主要分两步骤:
- 训练。给定一个数据集,每个样本包含一组特征和一个类别信息,然后调用分类算法训练分类模型。
- 预测。利用生成的模型或函数对新的数据集(测试集)进行分类预测,并判断其分类后的结果,并进行可视化绘图显示。
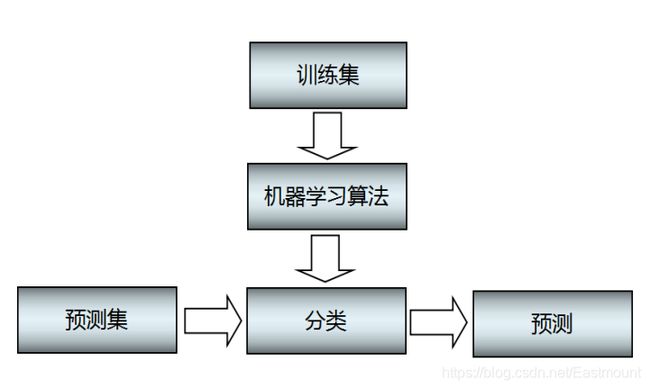
- 分类实例进行讲解。假设存在一个垃圾分类系统,将邮件划分为“垃圾邮件”和“非垃圾邮件”,现在有一个带有是否是垃圾邮件类标的训练集,然后训练一个分类模型,对测试集进行预测,步骤如下:
- (1)分类模型对训练集进行训练,判断每行数据是正向数据还是负向数据,并不断与真实的结果进行比较,反复训练模型,直到模型达到某个状态或超出某个阈值,模型训练结束。
- (2) 利用该模型对测试集进行预测,判断其类标是“垃圾邮件”还是“非垃圾邮件”,并计算出该分类模型的准确率和特征值。
经过上述的两步骤,当收到一封新邮件时,我们可以根据它邮件的内容或特征,判断其是否是垃圾邮件,更让我们便利减少垃圾邮件的骚扰。
2.常见的分类算法
监督式学习包括分类和回归。其中常见的分类算法包括朴素贝叶斯分类器、决策树、K最近邻分类算法、支持向量机、神经网络和基于规则的分类算法等,同时还有用于组合单一类方法的集成学习算法,如Bagging和Boosting等。
本节主要讲决策树:
决策树(Decision Tree)是以实例为基础的归纳学习(Inductive Learning)算法,它是对一组无次序、无规则的实例建立一棵决策判断树,并推理出树形结果的分类规则。决策树作为分类和预测的主要技术之一,其构造目的是找出属性和类别间的关系,用它来预测未知数据的类别。该算法采用自顶向下的递归方式,在决策树的内部节点进行属性比较,并根据不同属性值判断从该节点向下的分支,在决策树的叶子节点得到反馈的结果。
决策树算法根据数据的属性采用树状结构建立决策模型,常用来解决分类和回归问题。常见的算法包括:分类及回归树(CART算法)、ID3 、C4.5、随机森林等。
提示:以下是本篇文章正文内容,下面案例可供参考
一、决策树的基本概念
决策树是基于树结构来进行决策的,举个例子:
现有一位母亲急于给自己的女娃介绍一个男朋友,于是有了下面的对话:
1. 女儿:多大年纪了?
2. 母亲:26。
3. 女儿:长的帅不帅?
4. 母亲:挺帅的。
5. 女儿:收入高不?
6. 母亲:不算很高,中等情况。
7. 女儿:是公务员不?
8. 母亲:是,在税务局上班呢。
9. 女儿:那好,我去见见。
这个女孩的挑剔过程就是一个典型的决策树,即相当于通过年龄、长相、收入和是否公务员将男童鞋分为两个类别:见和不见。假设这个女孩对男人的要求是:30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员,那么使用下图就能很好地表示女孩的决策逻辑(即一颗决策树)。
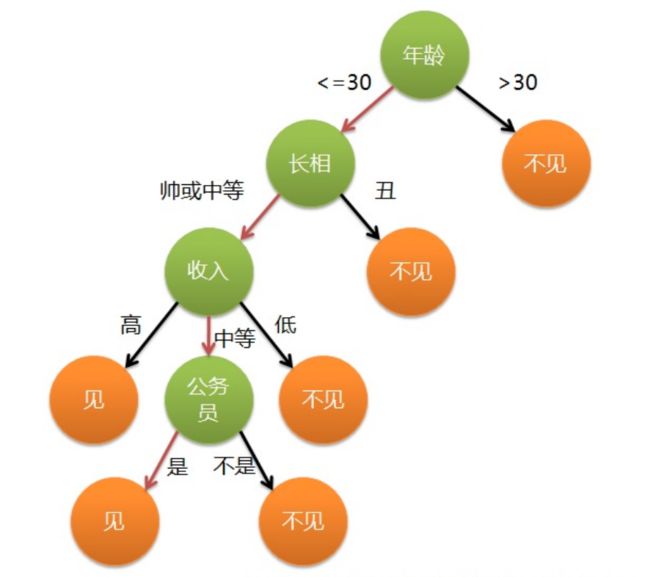
在上图的决策树中,决策过程的每一次判定都是对某一属性的“测试”,决策最终结论则对应最终的判定结果。一般一颗决策树包含:一个根节点、若干个内部节点和若干个叶子节点,易知:
- 每个非叶节点表示一个特征属性测试。
- 每个分支代表这个特征属性在某个值域上的输出。
- 每个叶子节点存放一个类别。
- 每个节点包含的样本集合通过属性测试被划分到子节点中,根节点包含样本全集。
决策树算法根据数据的属性并采用树状结构构建决策模型,常用来解决分类和回归问题。常见的决策树算法包括:
- ID3算法(IterativeDichotomiser 3)
- C4.5算法
- 分类及回归树(Classification And Regression Tree,简称CART)
- 随机森林算法(Random Forest
- 梯度推进机算法(GradientBoosting Machine,简称GBM)
对于CART、ID3和C4.5进行对比可得:
| 决策树 | 模型类型 | 树结构 | 特征选择 | 连续值处理 | 缺失处理 |
|---|---|---|---|---|---|
| ID3算法(IterativeDichotomiser 3) | 分类 | 多叉树 | 信息增益 | 不可以 | 不可以 |
| C4.5算法 | 分类 | 多叉树 | 信息增益比 | 可以 | 可以 |
| CART(Classification And Regression Tree) | 分类与回归 | 二叉树 | 基尼系数 | 可以 | 可以 |
决策树构建的基本步骤包括4步,具体步骤如下:
- 第一步:开始时将所有记录看作一个节点。
- 第二步:遍历每个变量的每一种分割方式,找到最好的分割点。
- 第三步:分割成两个节点N1和N2。
- 第四步:对N1和N2分别继续执行第二步和第三步,直到每个节点足够“纯”为止。
这里的优缺点是针对 CART 树来讲,因为现在 CART 是主流的决策树算法,而且在 sklearn 工具包中使
用的也是 CART 决策树。
优点:
- 非常直观,可解释极强。 在生成的决策树上,每个节点都有明确的判断分支条件,所以非常容易看到为什么要这样处理,比起神经网络模型的黑盒处理,高解释性的模型非常受金融保险行业的欢迎。
- 预测速度比较快。由于最终生成的模型是一个树形结构,对于一条新数据的预测,只需要按照条件在每一个节点进行判定就可以。通常来说,树形结构都有助于提升运算速度。
- 既可以处理离散值也可以处理连续值,还可以处理缺失值。
缺点:
- 容易过拟合。 在极端的情况下,我们根据样本生成了一个最完美的树,那么样本中出现的每一个值都会有一条路径来拟合,所以如果样本中存在一些问题数据,或者样本与测试数据存在一定的差距时,就会看出泛化性能不好,出现了过拟合的现象。
- 需要处理样本不均衡的问题。如果样本不均衡,某些特征的样本比例过大,最终的模型结果将会更偏向这些特征。
- 样本的变化会引发树结构巨变。
由于决策树容易过拟合,所以我们需要使用剪枝的方式来使得模型的泛化能力更好,剪枝可以理解为简化我们的决策树,是去掉不必要的节点路径以提高泛化能力。剪枝分为预剪枝和后剪枝:
- 预剪枝: 在决策树构建之初就设定一个阈值,当分裂节点的熵阈值小于设定值的时候就不再进行
分裂了;然而这种方法的实际效果并不是很好,因为谁也没办法预料到我们设定的恰好是我们想要 的。 - 后剪枝: 后剪枝方法就是在我们的决策树已经构建完成以后,再根据设定的条件来判断是否要合
并一些中间节点,使用叶子节点来代替。在实际的情况下,通常都是采用后剪枝的方案。
二、DTC算法
Sklearn机器学习包中,实现决策树(DecisionTreeClassifier,简称DTC)的类是:
sklearn.tree.DecisionTreeClassifier()
DecisionTreeClassifier构造方法为:
sklearn.tree.DecisionTreeClassifier(criterion='gini'
, splitter='best'
, max_depth=None
, min_samples_split=2
, min_samples_leaf=1
, max_features=None
, random_state=None
, min_density=None
, compute_importances=None
, max_leaf_nodes=None)
- criterion:特征选择标准[entropy, gini]。默认gini,即CART算法。
- splitter:特征划分标准,[best, random]。best在特征的所有划分点中找出最优的划分点,random随机的在部分划分点中找局部最优的划分点。默认的‘best’适合样本量不大的时候,而如果样本数据量非常大,此时决策树构建推荐‘random’。
- max_depth:决策树最大深度,[int, None]。默认值是‘None’。一般数据比较少或者特征少的时候可以不用管这个值,如果模型样本数量多,特征也多时,推荐限制这个最大深度,具体取值取决于数据的分布。常用的可以取值10-100之间,常用来解决过拟合。
- min_samples_split:内部节点(即判断条件)再划分所需最小样本数,[int, float]。默认值为2。如果是int,则取传入值本身作为最小样本数;如果是float,则取ceil(min_samples_split*样本数量)作为最小样本数。(向上取整)
- min_samples_leaf:叶子节点(即分类)最少样本数。如果是int,则取传入值本身作为最小样本数;如果是float,则取ceil(min_samples_leaf*样本数量)的值作为最小样本数。这个值限制了叶子节点最少的样本数,如果某叶子节点数目小于样本数,则会和兄弟节点一起被剪枝。
- max_features:在划分数据集时考虑的最多的特征值数量,[int值]。在每次split时最大特征数;[float值]表示百分数,即(max_features*n_features)
- random_state:[int, randomSate instance, None],默认是None
- min_density:默认None。
- compute_importances:默认None。
- max_leaf_nodes:最大叶子节点数。[int, None],通过设置最大叶子节点数,可以防止过拟合。默认值None,默认情况下不设置最大叶子节点数。如果加了限制,算法会建立在最大叶子节点数内最优的决策树。如果特征不多,可以不考虑这个值,但是如果特征多,可以加限制,具体的值可以通过交叉验证得到。
DecisionTreeClassifier类主要包括两个方法:
-
clf.fit(train_data,train_target) 用来装载(train_data,train_target)训练数据,并训练分类模型。
-
pre = clf.predict(test_data) 用训练得到的决策树模型对test_data测试集进行预测分析。
三、用决策树来分析鸢尾花
3.1数据集
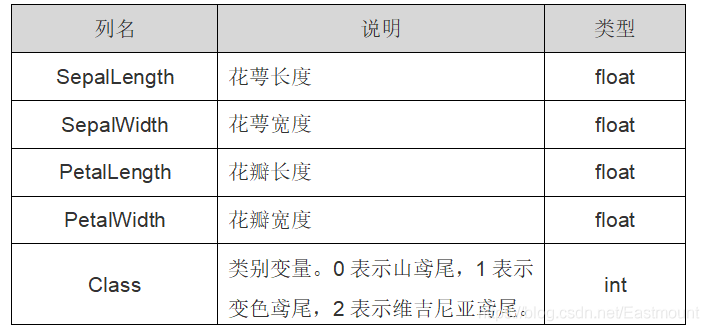
在Sklearn机器学习包中包含鸢尾花卉Iris数据集,它是一个很常用的数据集,共150行数据,包括四个特征变量:萼片长度、萼片宽度、花瓣长度、花瓣宽度。同时包括一个类别变量,将鸢尾花划分为三个类别,即:山鸢尾(Iris-setosa)、变色鸢尾(Iris-versicolor)、维吉尼亚鸢尾(Iris-virginica)。
iris数据集中包括两个属性iris.data和iris.target。其中,data数据是一个矩阵,每一列代表了萼片或花瓣的长宽,一共4列,每一行数据代表某个被测量的鸢尾植物,一共采样了150条记录。载入鸢尾花数据集代码如下所示:
from sklearn.datasets import load_iris # 导入数据集iris
iris = load_iris() # 载入数据集
# print(iris.data) # 输出iris数据
# print(iris.target) # 输出真实标签
3.2决策树分析鸢尾花
代码调用Sklearn机器学习包中DecisionTreeClassifier决策树算法进行分类分析,并绘制预测的散点图:
from sklearn.datasets import load_iris # 导入数据集iris
from sklearn.tree import DecisionTreeClassifier # 导入决策树DTC包
import numpy as np
import matplotlib.pyplot as plt
# 数据集
iris = load_iris()
# print(iris.data) # 输出数据集
print(iris.target) # 输出真实标签
print(len(iris.target)) # 输出真实标签的长度
print(iris.data.shape) # 150个样本 每个样本4个特征
# 模型
clf = DecisionTreeClassifier() # 构造决策模型
clf.fit(iris.data, iris.target) # 训练
predicted = clf.predict(iris.data) # 预测
# 获取花卉两列数据集
L1 = [x[0] for x in iris.data] # 获取了第一列数据集
L2 = [x[1] for x in iris.data] # 获取了第二列数据集
# 绘图
plt.scatter(L1, L2, c=predicted, marker='x') # cmap=plt.cm.Paired
plt.title("DTC")
plt.show()
输出为:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2]
150
(150, 4)
代码存在的缺点:
- 代码中通过“L1 = [x[0] for x in X]”获取了第一列和第二列数据集进行了分类分析和绘图,而真实的iris数据集中包括四个特征,那怎么绘制四个特征的图形呢?这就需要利用PCA降维技术处理。
- 第二个问题是在聚类、回归、分类模型中,都需要先进行训练,再对新的数据集进行预测,这里却是对整个数据集进行分类分析,而真实情况是需要把数据集划分为训练集和测试集的,例如数据集的70%用于训练、30%用于预测;或80%用于训练20%用于预测。
四、数据集划分和分类评估
主要是讲决策树分析鸢尾花代码的优化,对其数据集划分为预测集和训练集,以及对决策算法的分类评估。
Class 类别变量中0表示山鸢尾,1表示变色鸢尾,2表示维吉尼亚鸢尾。上述可知 print(iris.target) 为:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
调用NumPy库中的 concatenate() 函数对数据集进行挑选集成,选择第0-40行、第50-90行、第100-140行数据作为训练集,对应的类标作为训练样本类标;再选择第40-50行、第90-100行、第140-150行数据作为测试集合,对应的样本类标作为预测类标。代码如下:
# “axis=0”表示选取数值的等差间隔为0,即紧挨着获取数值。
#训练集
train_data = np.concatenate((iris.data[0:40, :], iris.data[50:90, :], iris.data[100:140, :]), axis = 0)
#训练集样本类别(真实标签)
train_target = np.concatenate((iris.target[0:40], iris.target[50:90], iris.target[100:140]), axis = 0)
#测试集
test_data = np.concatenate((iris.data[40:50, :], iris.data[90:100, :], iris.data[140:150, :]), axis = 0)
#测试集样本类别(真实标签)
test_target = np.concatenate((iris.target[40:50], iris.target[90:100], iris.target[140:150]), axis = 0)
调用sklearn机器学习包中metrics类对决策树分类算法进行评估,它将输出准确率(Precison)、召回率(Recall)、F特征值(F-score)、支持度(Support)等。
#输出准确率 召回率 F值
from sklearn import metrics
print(metrics.classification_report(test_target, predict_target))
print(metrics.confusion_matrix(test_target, predict_target))
分类报告函数为:
sklearn.metrics.classification_report(y_true,
y_pred,
labels=None,
target_names=None,
sample_weight=None,
digits=2)
参数作用:
y_true参数表示正确的分类类标,
y_pred表示分类预测的类标,
labels表示分类报告中显示的类标签的索引列表,
target_names参数显示与labels对应的名称,
digits是指定输出格式的精确度。
调用 metrics.classification_report() 方法对决策树算法进行评估后,会在最后一行将对所有指标进行加权平均值,代码如下:
from sklearn.datasets import load_iris # 导入数据集iris
from sklearn.tree import DecisionTreeClassifier # 导入决策树DTC包
from sklearn import metrics
import numpy as np
import matplotlib.pyplot as plt
#导入数据集iris
'''
重点:分割数据集 构造训练集/测试集,80/20
70%训练 0-40 50-90 100-140
30%预测 40-50 90-100 140-150
'''
iris = load_iris()
train_data = np.concatenate((iris.data[0:40, :], iris.data[50:90, :], iris.data[100:140, :]), axis = 0) # 训练集
train_target = np.concatenate((iris.target[0:40], iris.target[50:90], iris.target[100:140]), axis = 0) # 训练集样本类别
test_data = np.concatenate((iris.data[40:50, :], iris.data[90:100, :], iris.data[140:150, :]), axis = 0) # 测试集
test_target = np.concatenate((iris.target[40:50], iris.target[90:100], iris.target[140:150]), axis = 0) # 测试集样本类别
# 导入决策树DTC包
clf = DecisionTreeClassifier()
clf.fit(train_data, train_target) # 注意均使用训练数据集和样本类标
# print(clf)
predict_target = clf.predict(test_data) # 测试集
print(predict_target)
# 预测结果与真实结果比对
print(sum(predict_target == test_target))
# 输出准确率(Precison)、召回率(Recall)、F特征值(F-score)、支持度(Support)
print(metrics.classification_report(test_target, predict_target))
print(metrics.confusion_matrix(test_target, predict_target)) # 计算混淆矩阵
# 获取花卉测试数据集两列数据
X = test_data
L1 = [n[0] for n in X]
L2 = [n[1] for n in X]
# 绘制散点图
plt.scatter(L1, L2, c=predict_target, marker='x') #cmap=plt.cm.Paired
plt.title("DecisionTreeClassifier")
plt.show()
输出为结果如下,包括对数据集40-50、90-100、140-150的预测结果,接下来输出的“30”表示整个30组类标预测结果和真实结果是一致的,最后输出评估结果。
[0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2]
30
precision recall f1-score support
0 1.00 1.00 1.00 10
1 1.00 1.00 1.00 10
2 1.00 1.00 1.00 10
accuracy 1.00 30
macro avg 1.00 1.00 1.00 30
weighted avg 1.00 1.00 1.00 30
[[10 0 0]
[ 0 10 0]
[ 0 0 10]]
散点图为:
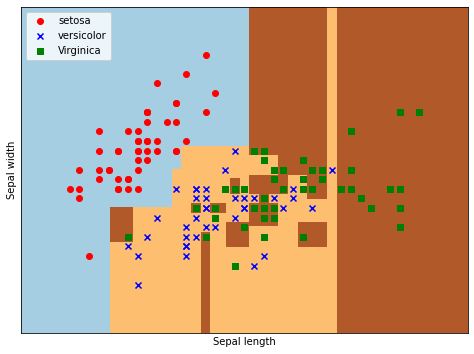
五、区域划分对比
将鸢尾花数据集共分为三个区域,最后进行散点图绘制对比。每个区域对应一类散点,表示预测结果和真实结果一致,如果某个区域混入其他类型的散点,则表示该点的预测结果与真实结果不一致。
决策树分类分析:
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
# 载入鸢尾花数据集
iris = load_iris()
X = X = iris.data[:, :2] # 获取花卉前两列数据
Y = iris.target
lr = DecisionTreeClassifier() # 决策树模型
lr.fit(X,Y) # 训练数据X,Y
# meshgrid函数生成两个网格矩阵
h = .02 # 步长h(设置为0.02)
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5 # 取X二维数组的第一列(长度)的最小值、最大值
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5 # 取X二维数组的第二列(长度)的最小值、最大值
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))# 先取上面x和y变为数组,再由meshgrid函数生成两个网格矩阵xx和yy
# pcolormesh函数将xx,yy两个网格矩阵和对应的预测结果Z绘制在图片上
Z = lr.predict(np.c_[xx.ravel(), yy.ravel()]) # 将xx和yy矩阵都变成两个一维数组,调用np.c_[]函数组合成一个二维数组进行预测
Z = Z.reshape(xx.shape) # 调用reshape()函数修改形状,将其Z转换为两个特征(长度和宽度)
plt.figure(1, figsize=(8,6))
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired) # 调用pcolormesh()函数来分类区域画图
# 绘制散点图
plt.scatter(X[:50,0], X[:50,1], color='red',marker='o', label='setosa')
# # 第一个参数为第一列数据(长度),第二个参数为第二列数据(宽度),第三、四个参数为设置点的颜色为红色,款式o为圆圈,最后标记为setosa。
plt.scatter(X[50:100,0], X[50:100,1], color='blue', marker='x', label='versicolor')
plt.scatter(X[100:,0], X[100:,1], color='green', marker='s', label='Virginica')
plt.xlabel('Sepal length') # x的标题
plt.ylabel('Sepal width') # y的标题
plt.xlim(xx.min(), xx.max()) # x轴的范围
plt.ylim(yy.min(), yy.max()) # y轴的范围
plt.xticks(()) # x轴的标度为空
plt.yticks(()) # y轴的标度为空
plt.legend(loc=2)
plt.show()
代码部分细讲:
-
获取的鸢尾花两列数据,对应为萼片长度和萼片宽度,每个点的坐标就是(x,y)。先取X二维数组的第一列(长度)的最小值、最大值和步长h(设置为0.02)生成数组,再取X二维数组的第二列(宽度)的最小值、最大值和步长h生成数组,最后用meshgrid()函数生成两个网格矩阵xx和yy。
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
print(xx)
print(yy)
# 输出为
[[3.8 3.82 3.84 ... 8.36 8.38 8.4 ]
[3.8 3.82 3.84 ... 8.36 8.38 8.4 ]
[3.8 3.82 3.84 ... 8.36 8.38 8.4 ]
...
[3.8 3.82 3.84 ... 8.36 8.38 8.4 ]
[3.8 3.82 3.84 ... 8.36 8.38 8.4 ]
[3.8 3.82 3.84 ... 8.36 8.38 8.4 ]]
-
调用ravel()函数将xx和yy的两个矩阵转变成一维数组,再进行预测分析。由于两个矩阵大小相等,因此两个一维数组大小也相等。np.c_[xx.ravel(), yy.ravel()]是生成矩阵。是先把第一列萼片长度数据按h取等分作为行,并复制多行得到xx网格矩阵;再把第二列萼片宽度数据按h取等分,作为列,并复制多列得到yy网格矩阵;最后将xx和yy矩阵都变成两个一维数组,调用np.c_[]函数组合成一个二维数组矩阵进行预测。
Z = lr.predict(np.c_[xx.ravel(), yy.ravel()]) # 将xx和yy矩阵都变成两个一维数组,调用np.c_[]函数组合成一个二维数组进行预测
print(xx.ravel())
print(yy.ravel())
print(np.c_[xx.ravel(), yy.ravel()])
print(Z)
# 输出为
XX为[3.8 3.82 3.84 ... 8.36 8.38 8.4 ]
yy为[1.5 1.5 1.5 ... 4.9 4.9 4.9]
二维数组矩阵为
[[3.8 1.5 ]
[3.82 1.5 ]
[3.84 1.5 ]
...
[8.36 4.9 ]
[8.38 4.9 ]
[8.4 4.9 ]]
预测值Z为[0 0 0 ... 2 2 2]
-
调用reshape()函数修改形状,将其Z转换为两个特征(长度和宽度),则39501个数据转换为171*231的矩阵。Z = Z.reshape(xx.shape)输出如下:
print(Z.size)
Z = Z.reshape(xx.shape) # 调用reshape()函数修改形状,将其Z转换为两个特征(长度和宽度)
print(Z)
# 输出为
size:39501
[[0 0 0 ... 2 2 2]
[0 0 0 ... 2 2 2]
[0 0 0 ... 2 2 2]
...
[0 0 0 ... 2 2 2]
[0 0 0 ... 2 2 2]
[0 0 0 ... 2 2 2]]
-
pcolormesh()函数将xx、yy两个网格矩阵和对应的预测结果Z绘制在图片上,输出为三个颜色区块,分别表示三类区域。cmap=plt.cm.Paired表示绘图样式选择Paired主题。
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired) # 调用pcolormesh()函数来分类区域画图
plt.show()
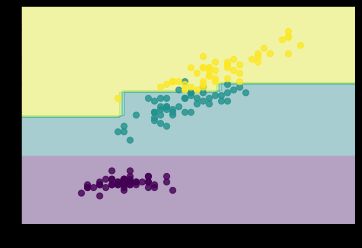
六、使用pydotplus可视化决策树
- 这里给一个限制决策树层数为4的DecisionTreeClassifier例子。
from itertools import product
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
# 仍然使用自带的iris数据
iris = datasets.load_iris()
X = iris.data[:, [0, 2]]
y = iris.target
# 训练模型,限制树的最大深度4
clf = DecisionTreeClassifier(max_depth=4)
#拟合模型
clf.fit(X, y)
# 画图
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
np.arange(y_min, y_max, 0.1))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, alpha=0.8)
plt.show()
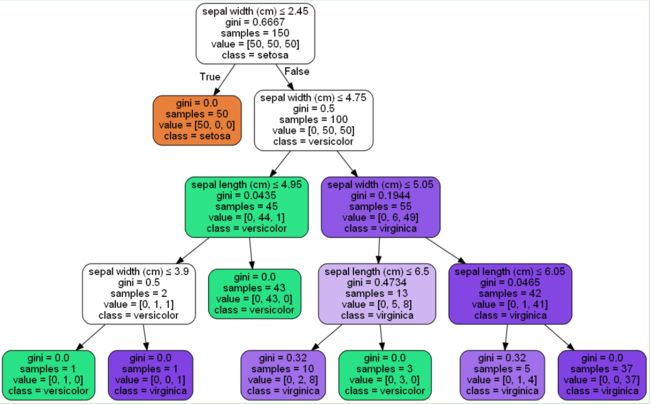
- 接着我们可视化我们的决策树
from IPython.display import Image
from sklearn import tree
import pydotplus
dot_data = tree.export_graphviz(clf, out_file=None,
feature_names=iris.feature_names,
class_names=iris.target_names,
filled=True, rounded=True,
special_characters=True)
graph = pydotplus.graph_from_dot_data(dot_data)
Image(graph.create_png())
总结
- 随机森林:为了更好地解决泛化及树结构变动~ 等 ~问题,从决策树演进出来随机森林算法。根据 我们前面讲的模型集成方法,随机森林就是使用了 bagging 方案构建了多棵决策树,然后对所有 树的结果来进行平均计算以获得最终的结果。
- GBDT:在随机森林的基础上,研究者又提出了梯度提升决策树算法(Gradient Boosting Decision
Tree,GBDT),GBDT 是基于 boosting 的策略。与随机森林一样的是,GBDT 也会构 建多棵决策树;但不同的是,GBDT构建的多棵树之间是有联系的,每个分类器在上一轮分类器的 残差基础上进行训练。(后续会写到) - XGBoost:一个非常火热的模型,有 “机器学习大杀器” 之称,在很多比赛中都获得了非常好的结 果。但实际上 XGBoost不算是一个算法,而是对 GBDT 的一种工程实现,它优化了 GBDT 里面的
求解过程,并加入了很多工程上的优化项目,使得数据处理、运算速度等环节都有了很大的提升。