数学工具构造器
数学工具构造器

【科学刷题】完全吃透所有栈相关的算法题

https://leetcode-cn.com/tag/stack/problemset/

文章目录

  • 1 常规的栈相关题目
    • 1.1 括号匹配
      • 1.1.1 有效的括号
      • 1.1.2 移除无效的括号
    • 1.2 基于栈的模拟题
      • 1.2.1 原子的数量
      • 1.2.2 反转每对括号间的子串
      • 1.2.3 括号的分数
      • 1.2.4 字符串解码
    • 1.3 栈的压入、弹出序列
    • 1.4 表达式求值
      • 1.4.1 逆波兰表达式求值
      • 1.4.2 基本计算器
        • 1.4.2.1 加减号 + 小括号
        • 1.4.2.2 加减号 + 乘除号 + 小括号
    • 1.5 删除字符串中的所有相邻重复项
  • 2 DP + 栈
    • 2.1 最长有效括号
  • 3 栈的排序
  • 4 最小/最大 --- 栈/队列
    • 4.1 最小栈（常数时间求minOfStack）
    • 4.2 最大栈（常数时间求maxOfStack + popMax）
    • 4.3 队列的最大值
  • 5 单调栈 / 单调队列
    • 5.1 单调栈
      • 5.1.1 柱状图中的最大矩形 --- 从2次遍历到1次遍历，从1维到2维
        • 5.1.1.1 柱状图中最大的矩形
        • 5.1.1.2 [01矩阵]中的 最大矩形
      • 5.1.3 下一个更大元素 --- 从线形到环形
        • 5.1.3.1 【线形】下一个更大元素
        • 5.1.3.2 【环形】下一个更大元素
      • 5.1.4 求[长为K]字典序最小(最大)的子序列 --- 从1维到2维
        • 5.1.4.1 保留长度为N-K的子序列
        • 5.1.4.2 拼接最大数
      • 5.1.5 不同字符的最小子序列
      • 5.1.6 股票价格跨度
    • 5.2 单调队列
      • 5.2.1 队列的最大值
      • 5.2.2 滑动窗口最大值
  • 6 栈与队列的相互转换
    • 6.1 两个栈实现队列
    • 6.2 队列实现栈

1 常规的栈相关题目

1.1 括号匹配

1.1.1 有效的括号

20. 有效的括号

微软一面考过这题

扫描，左括号入栈，右括号与栈顶元素比较，如果能匹配上就消掉

class Solution:
    def isValid(self, s: str) -> bool:
        stack=collections.deque()
        mapper={
            ')':'(',
            '}':'{',
            ']':'[',
        }
        for c in s:
            if c in mapper:
                if not stack:
                    return False
                if mapper[c]!=stack.pop():
                    return False
            else:
                stack.append(c)
        return not stack # 这里写错

1.1.2 移除无效的括号

1249. 移除无效的括号

无效括号分两种情况：

  1. 多余的)：如果栈顶出现)，说明多余了
  2. 多余的(：如果迭代完成后stack非空，说明(多余了

基于这两点认识，我们可以写以下代码：

class Solution:
    def minRemoveToMakeValid(self, s: str) -> str:
        stack = []
        s = list(s)
        for i, c in enumerate(s):
            if c == "(":
                stack.append(i)
            elif c == ")":
                if stack:
                    stack.pop()
                else:
                    s[i] = ''
        for i in stack:
            s[i] = ''
        return ''.join(s)

1.2 基于栈的模拟题

这类题目都有一个共同的特点：

  1. 需要用一个栈来模拟题设的操作（一般来说是括号匹配之类的），并且这个栈通常会有一个初始元素，表示root或者最顶层的值（对照3，思考为什么）
  2. 遇到左括号，会初始化一个元素，然后push到栈顶
  3. 遇到右括号，会pop栈顶元素，在做一些必要的操作后，更新到此时的栈顶元素（注意不是刚刚pop的栈顶元素）
  4. 遇到其他字符，会对栈顶元素进行操作

1.2.1 原子的数量

726. 原子的数量

扫描每个字符：

  • 如果是左括号，则需要新开一个计数器去记录当前括号内的原子数，将计数器push到栈顶
  • 如果是右括号，弹出栈顶计数器top，然后扫描出括号右边的原子数，用这个原子数对top计数器进行更新，合并到栈顶计数器。
  • 如果是其他字符，解析出原子-原子数的KV对，并对栈顶的计数器进行更新
class Solution:
    def countOfAtoms(self, formula: str):
        N = len(formula)
        stack = [Counter()]
        i = 0
        while i < N:
            if formula[i] == "(":
                stack.append(Counter())
                i += 1
            elif formula[i] == ")":
                top = stack.pop()
                i += 1
                i_start = i
                while i < N and formula[i].isdigit():
                    i += 1
                multi = int(formula[i_start:i] or 1)
                for name, cnt in top.items():
                    stack[-1][name] += cnt * multi
            else:
                i_start = i
                i += 1
                while i < N and formula[i].islower():
                    i += 1
                name = formula[i_start:i]
                i_start = i
                while i < N and formula[i].isdigit():
                    i += 1
                multi = int(formula[i_start:i] or 1)
                stack[-1][name] += multi
        return "".join(name + (str(stack[-1][name]) if stack[-1][name] > 1 else '')
                       for name in sorted(stack[-1]))

1.2.2 反转每对括号间的子串

1190. 反转每对括号间的子串

class Solution:
    def reverseParentheses(self, s: str) -> str:
        stack = [""]
        for chr in s:
            if chr == "(":
                stack.append("")
            elif chr == ")":
                top = stack.pop()
                stack[-1] += top[::-1]
            else:
                stack[-1] += chr
        return stack[-1]

1.2.3 括号的分数

856. 括号的分数

一道机器学习岗位面试题：求圆上任取三个点组成锐角三角形的概率

class Solution:
    def scoreOfParentheses(self, S: str) -> int:
        stack = [0]
        for c in S:
            if c == "(":
                stack.append(0)
            else:
                val = stack.pop()
                if val == 0: # 可以视为“叶子结点”
                    delta = 1
                else:       # 可以视为“非叶子结点”
                    delta = val * 2
                stack[-1] += delta
        return stack[0]

1.2.4 字符串解码

394. 字符串解码

class Solution:
    def decodeString(self, s: str) -> str:
        stack = [["", 0]]
        for c in s:
            if c.isdigit():
                stack[-1][1] = stack[-1][1] * 10 + int(c)
            elif c == "[":
                stack.append(["", 0])
            elif c == "]":
                string, _ = stack.pop()
                times = stack[-1][1]
                if times == 0:
                    times = 1
                stack[-1][0] += string * times
                stack[-1][1] = 0
            else:
                stack[-1][0] += c
        return stack[0][0]

1.3 栈的压入、弹出序列

剑指 Offer 31. 栈的压入、弹出序列

946. 验证栈序列

面试题31. 栈的压入、弹出序列（模拟，清晰图解）

好家伙，看了题解才知道我的思路是反过来的，居然还能AC

class Solution:
    def validateStackSequences(self, pushed: List[int], popped: List[int]) -> bool:
        stack = []
        i = 0
        for num in pushed:
            stack.append(num)
            while stack and stack[-1] == popped[i]:
                stack.pop()
                i += 1
        return not stack

1.4 表达式求值

1.4.1 逆波兰表达式求值

150. 逆波兰表达式求值

class Solution:
    def evalRPN(self, tokens: List[str]) -> int:
        token2op = {
            '*': mul,
            '-': sub,
            '+': add,
            '/': lambda x, y: int(x / y)
        }
        stack = []
        for token in tokens:
            try:
                num = int(token)
            except:
                y = stack.pop()  # 注意顺序是反过来的
                x = stack.pop()
                num = token2op[token](x, y)
            finally:
                stack.append(num)
        return stack[0]

1.4.2 基本计算器

1.4.2.1 加减号 + 小括号

224. 基本计算器

如何想到用「栈」？思路来自于递归

只有加减号 + 小括号的话，边界条件比较简单，我们可以采用1.2 基于栈的模拟题的思路，栈中元素为一个tuple，下标0表示sign，下标1表示res结果

这种思路基本正确，只需要微调就可以用在有 乘除号 的情况中了

class Solution:
    def calculate(self, s: str) -> int:
        # sign, res, num
        stack = [[1, 0, 0]]

        def update_num_to_res(stack):
        	# res += num * sign
            stack[-1][1] += stack[-1][2] * stack[-1][0]
            stack[-1][2] = 0

        for c in s:
            if c == "(":
                stack.append([1, 0, 0])
            elif c == ")":
                update_num_to_res(stack) # 括号闭合时更新
                _, res, _ = stack.pop()
                stack[-1][2] = res # 当前括号中算出的res更新到栈顶的num中
            elif c in ("-", "+"):
                update_num_to_res(stack) # 遇到符号时更新
                stack[-1][0] = 1 if c == "+" else -1
            elif c.isdigit():
                num = stack[-1][2]
                num = num * 10 + int(c)
                stack[-1][2] = num
        update_num_to_res(stack)  # 根节点解析结束时更新
        return stack[0][1]

1.4.2.2 加减号 + 乘除号 + 小括号

772. 基本计算器 III

注：1+2*-3无法通过

拆解复杂问题：实现计算器

做了两个修改：

  1. sign → \rightarrow → op (operator)
  2. res → \rightarrow → num_stack （栈里面套栈，用来解决优先级的问题）
  3. return res → \rightarrow → return sum(num_stack)
class Solution:
    def calculate(self, s: str) -> int:
        # op, num_stack, num
        stack = [['+', [], 0]]
        operators = ['+', '-', '*', '/']

        def update_num_to_res(stack):
            # num_stack 对象引用，不用显式更新
            op, num_stack, num = stack[-1]
            if op == '+':
                num_stack.append(num)
            elif op == '-':
                num_stack.append(-num)
            elif op in ('*', '/'):
                x = num_stack.pop()
                y = num
                if op == '*':
                    num_stack.append(x * y)
                else:
                    num_stack.append(int(x / y))
            # num需要显示更新，置为0
            stack[-1][2] = 0

        for c in s:
            if c == "(":
                # op, num_stack, num
                stack.append(['+', [], 0])
            elif c == ")":
                update_num_to_res(stack)  # 括号闭合时更新
                _, res, _ = stack.pop()
                stack[-1][2] = sum(res)  # 当前括号中算出的res更新到栈顶的num中
            elif c in operators:
                update_num_to_res(stack)  # 遇到符号时更新
                stack[-1][0] = c
            elif c.isdigit():
                num = stack[-1][2]
                num = num * 10 + int(c)
                stack[-1][2] = num
        update_num_to_res(stack)  # 根节点解析结束时更新
        return sum(stack[0][1])

1.5 删除字符串中的所有相邻重复项

1047. 删除字符串中的所有相邻重复项

class Solution:
    def removeDuplicates(self, s: str) -> str:
        stack = []
        for c in s:
            if stack and c == stack[-1]:
                stack.pop()
            else:
                stack.append(c)
        return "".join(stack)

1209. 删除字符串中的所有相邻重复项 II

class Solution:
    def removeDuplicates(self, s: str, k: int) -> str:
        stack = [1]
        n = len(s)
        res = s[0]
        for i in range(1, n):
            res += s[i]
            if len(res) >= 2 and res[-1] == res[-2]:
                stack[-1] += 1
            else:
                stack.append(1)
            if stack[-1] == k:
                stack.pop()
                res = res[:-k]
        return res

2 DP + 栈

2.1 最长有效括号

32. 最长有效括号

  • DP
class Solution:
    def longestValidParentheses(self, s: str) -> int:
        n = len(s)
        dp = [0] * n
        ans = 0
        for i in range(n):
            if i > 0 and s[i] == ')':
                if s[i - 1] == "(" and i - 2 >= 0:
                    dp[i] = dp[i - 2] + 2
                else:
                    pre_len = dp[i - 1]
                    match_ix = i - pre_len - 1
                    if match_ix >= 0 and s[match_ix] == '(':
                        dp[i] = dp[i - 1] + 2
                        if match_ix - 1 >= 0:
                            dp[i] += dp[match_ix - 1]
                ans = max(ans, dp[i])
        return ans
  • 栈

32. 最长有效括号，辅助栈

class Solution:
    def longestValidParentheses(self, s: str) -> int:
        stack = [-1]
        res = 0
        for i, chr in enumerate(s):
            if len(stack) > 1 and chr == ")" and s[stack[-1]] == "(":
                stack.pop()
                res = max(res, i - stack[-1])
            else:
                stack.append(i)
        return res

3 栈的排序

面试题 03.05. 栈排序

猿辅导、美团、字节面试题——双栈排序

要求stack2（辅助栈）从栈底到栈顶是单调递增的

def stackSort(stack1):
    stack2 = []
    while stack1:
        # 取出 【栈1】 的 【栈顶元素】
        top = stack1.pop()
        # 不满足【单调递增】的条件
        # 看起来【stack2】从栈底到栈顶是【单调递减】的
        while stack2 and stack2[-1] > top:
            t = stack2.pop()
            stack1.append(t) # pop 掉这个元素，扔 stack1 中
        # 将 【栈1】 的 【栈顶元素】 push到【栈2】
        stack2.append(top)
    return stack2

4 最小/最大 — 栈/队列

4.1 最小栈（常数时间求minOfStack）

155. 最小栈

剑指 Offer 30. 包含min函数的栈

【科学刷题】完全吃透所有栈相关的算法题_第1张图片

最小栈 （辅助栈法，清晰图解）

时间复杂度 O ( 1 ) O(1) O(1)，空间复杂度 O ( N ) O(N) O(N)

维护一个单调递减的辅助栈B：

  • 入栈：如果元素x满足在B上单调递减，入栈
  • 出栈：如果A出栈元素等于B栈顶元素，出栈

因为栈是访问受限的线性数据结构，即只能从栈顶访问栈。所以只能访问栈顶。

如果这题改为最小队列（常数时间求minOfQueue），应该仿照单调栈的做法，维护一个单调递增的双端队列，这样如果一个比当前元素都要小的元素（新的min-value）入队后，会从队尾将队列中所有元素pop掉，min-value成为新的队头。

class MinStack:

    def __init__(self):
        """
        initialize your data structure here.
        """
        self.A = []
        self.B = []


    def push(self, x: int) -> None:
    	# 栈A正常push
        self.A.append(x)
        # 如果栈B元素空，或者x小于栈B的栈顶，push到栈B
        # 目的是维护栈B为一个单调递减（从栈底到栈顶）的栈
        if (not self.B) or x <= self.B[-1]:
            self.B.append(x)


    def pop(self) -> None:
    	# 栈A正常出栈
        top = self.A.pop()
        # 如果A的出栈元素恰为栈B的栈顶元素，B也出栈
        if self.B and top == self.B[-1]:
            self.B.pop()

	# A B 的peak函数正常执行
    def top(self) -> int:
        return self.A[-1]


    def getMin(self) -> int:
        return self.B[-1]

4.2 最大栈（常数时间求maxOfStack + popMax）

716. 最大栈

  • 双栈法

因为popMax的存在，这个操作需要不断出栈直到找到最大元素，然后再push回来，时间复杂度为 O ( N ) O(N) O(N)

class MaxStack(list):
    def push(self, x):
        m = max(x, self[-1][1] if self else None)
        self.append((x, m))

    def pop(self):
        return list.pop(self)[0]

    def top(self):
        return self[-1][0]

    def peekMax(self):
        return self[-1][1]

    def popMax(self):
        m = self[-1][1]
        b = []
        while self[-1][0] != m:
            b.append(self.pop())

        self.pop()
        map(self.push, reversed(b))
        return m
  • 双向链表 + 平衡树

【科学刷题】完全吃透所有栈相关的算法题_第2张图片
TODO: 用C++实现

4.3 队列的最大值

剑指 Offer 59 - II. 队列的最大值

如果是最小队列，应该用单调栈的方法维护一个单调递增的双端队列。在4.1阐述过

如果是最大队列，应该用单调栈的方法维护一个单调递减的双端队列。本题就是这个思路

class MaxQueue:

    def __init__(self):
        self.queue = collections.deque()
        # monotonous queue
        self.monoq = collections.deque()


    def max_value(self) -> int:
        return self.monoq[0] if self.monoq else -1


    def push_back(self, value: int) -> None:
        # 单调递减队列 (前一个元素大于等于后一个元素)
        # fixme: 老是把if 写成 while
        # 相当于：  not self.monoq[-1] >= value 即不满足单调递减的条件
        while self.monoq and self.monoq[-1] < value:
            self.monoq.pop()
        self.monoq.append(value)
        self.queue.append(value)


    def pop_front(self) -> int:
        if not self.queue:
            return -1
        left = self.queue.popleft()
        if self.monoq[0] == left:
            self.monoq.popleft()
        return left

5 单调栈 / 单调队列

5.1 单调栈

5.1.1 柱状图中的最大矩形 — 从2次遍历到1次遍历，从1维到2维

5.1.1.1 柱状图中最大的矩形

84. 柱状图中最大的矩形

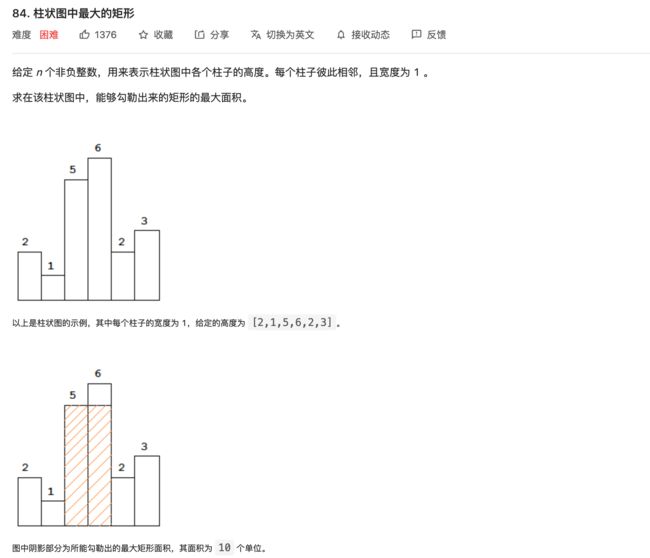【科学刷题】完全吃透所有栈相关的算法题_第3张图片对于每个元素，往左找到第一个小于这个元素的下标，往右找到第一个小于这个元素的下标

从左往右，维护一个单调递增栈，这样当前元素入栈前，栈中所有大于当前元素的元素都pop掉了，只剩下小于当前元素的最近元素

所以我们可以做两个栈出来：

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        n = len(heights)
        # left -> right
        stack = []
        left = []
        for i in range(n):
            # 不满足【严格单调递增】
            while stack and (not heights[stack[-1]] < heights[i]):
                stack.pop()
            left.append(stack[-1] if stack else -1)
            stack.append(i)
        print(left)
        # right -> left
        stack = []
        right = [n for i in range(n)]
        for i in range(n - 1, -1, -1):
            while stack and (not heights[stack[-1]] < heights[i]):
                stack.pop()
            # 用append就错啦
            right[i] = (stack[-1] if stack else n)
            stack.append(i)
        print(right)
        # calc
        ans = 0
        for i in range(n):
            ans = max(ans, (right[i] - left[i] - 1) * heights[i])
        return ans

我们可以将2个单调栈 + 2次遍历 化简为 1个单调栈 + 1次遍历 ：

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        n = len(heights)
        # left -> right
        stack = []
        left = [-1 for i in range(n)]
        right = [n for i in range(n)]
        for i in range(n):
            # 不满足【严格单调递增】
            while stack and (not heights[stack[-1]] < heights[i]):
                right[stack.pop()] = i
            left[i] = (stack[-1] if stack else -1)
            stack.append(i)
        ans = 0
        for i in range(n):
            ans = max(ans, (right[i] - left[i] - 1) * heights[i])
        return ans

5.1.1.2 [01矩阵]中的 最大矩形

注：[01矩阵]中的 最大正方形 用DP做：
221. 最大正方形

85. 最大矩形

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        N = len(heights)
        left = [0] * N
        right = [N] * N
        stack = []
        for i in range(N):
            while stack and heights[stack[-1]] > heights[i]:
                right[stack.pop()] = i
            left[i] = stack[-1] if stack else -1
            stack.append(i)
        return max(heights[i] * (right[i] - left[i] - 1) for i in range(N))

    def maximalRectangle(self, matrix: List[List[str]]) -> int:
        N = len(matrix)
        if not N:
            return 0
        M = len(matrix[0])
        if not M:
            return 0
        heights = [0] * M
        ans = 0
        for i in range(N):
            for j in range(M):
                if matrix[i][j] == "1":
                    heights[j] += 1
                else:
                    heights[j] = 0
            ans = max(ans, self.largestRectangleArea(heights))
        return ans

5.1.3 下一个更大元素 — 从线形到环形

5.1.3.1 【线形】下一个更大元素

496. 下一个更大元素 I

在5.1.1.1 柱状图中最大的矩形中，我们讨论了：要找到左边第一个更小元素，需要维护一个单调递增栈。

而要找下一个最大元素，应该从右往左，维护一个单调递减栈。这样新元素入栈前，会把所以小于新元素的元素pop掉（保证新元素<栈顶元素，从而满足单调递减），此时的栈顶元素就是要找的下一个最大元素

class Solution:
    def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
        nums = nums2
        mp = {}
        # ---------------------
        # 单调递减栈
        stack = []
        L = len(nums)
        ans = [0] * L
        for i in range(L - 1, -1, -1):
            num = nums[i]
            # 不满足【单调递减】
            while stack and (not stack[-1] > num):
                stack.pop()
            ans[i] = stack[-1] if stack else -1
            stack.append(num)
            # 缓存
            mp[num] = ans[i]
        # -----------------------
        return [mp[x] for x in nums1]

739. 每日温度

这题和【下一个更大元素】基本一致

class Solution:
    def dailyTemperatures(self, T: List[int]) -> List[int]:
        nums = T
        # -------------------------
        # 单调递减栈
        stack = []
        L = len(nums)
        ans = [0] * L
        for i in range(L - 1, -1, -1):
            num = nums[i]
            # 不满足【单调递减】
            while stack and (not nums[stack[-1]] > num):
                stack.pop()
            ans[i] = stack[-1] - i if stack else 0
            stack.append(i)
        return ans

5.1.3.2 【环形】下一个更大元素

难度升级为【环形】的题目还有：
打家劫舍2
环形的【跳台阶】，一个字节面试题
环形取石子，区间DP

503. 下一个更大元素 II

【科学刷题】完全吃透所有栈相关的算法题_第4张图片

[1,  2,  1,  1,  2,  1]
[2, -1,  2 , 2 ,-1 ,-1]

从右往左，覆盖老元素

class Solution:
    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        stack = []
        L = len(nums)
        ans = [0] * L
        for i in range(L * 2 - 1, -1, -1):
            num = nums[i % L]
            while stack and (not stack[-1] > num):
                stack.pop()
            ans[i % L] = stack[-1] if stack else -1
            stack.append(num)
        return ans

5.1.4 求[长为K]字典序最小(最大)的子序列 — 从1维到2维

这种类型的题就比5.1.1 ，5.1.2 这样的题更简单，或者说更直白一些：

  1. 如果需要得到一个字典序最小的子序列，维护单调递增栈，（即最小的元素放在最前面，字典序最小）
  2. 如果需要得到一个字典序最大的子序列，维护单调递减栈

5.1.4.1 保留长度为N-K的子序列

402. 移掉K位数字

移除这个数中的 k 位数字，使得剩下的数字最小。

首先要理解题意， 求 N − K N-K N−K个最小的数

思维转变， 把丢弃视为保留

删除第一个不单调递增（开始下降， num[x] < num[x-1]）

class Solution:
    def removeKdigits(self, num: str, k: int) -> str:
    	# 单调递增栈
        numStack = []
        for digit in num:
        	# 相比普通单调栈，多个k这个判断条件
        	#                        不满足于【单调递增】
            while k and numStack and (not numStack[-1] <= digit):
                numStack.pop()
                k -= 1 # 最多只能pop k个，等同于保留N-K个
            numStack.append(digit)
        # 特殊情况： 单调递增的num
        # [:-k]  等同于删除末尾的k个数字
        finalStack = numStack[:-k] if k else numStack
        # 特殊情况：前导0
        #  or "0" 这步相当妙，默写的时候没默出来
        return "".join(finalStack).lstrip("0") or "0"

5.1.4.2 拼接最大数

321. 拼接最大数

出现频率较小，有空再研究一下这题

class Solution:
    def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]:
        def pick_max(lst, k):
            stack = []
            drop = len(lst) - k  # 没想到
            for e in lst:
                # 没想到
                while drop and stack and stack[-1] < e:
                    stack.pop()
                    drop -= 1  # 没想到
                stack.append(e)
            return stack[:k]  # 没想到截断 (2次)

        def merge(la, lb):
            res = []
            # 为的是解决 [6, 7], [6, 0, 4] 这样的case
            while la or lb:
                # bigger 保证不为空列表
                bigger = la if la > lb else lb
                res.append(bigger.pop(0))  # 简写
                # bigger.pop(0) # 简写
            return res

        ret = []
        for sp in range(k + 1):
            # 判断条件的 <= 写错为 < 
            if sp <= len(nums1) and k - sp <= len(nums2):
                tmp = merge(
                    pick_max(nums1, sp),
                    pick_max(nums2, k - sp),
                )
                ret = max(ret, tmp)
        return ret

5.1.5 不同字符的最小子序列

316. 去除重复字母

1081. 不同字符的最小子序列

counter表示剩余未遍历字符的出现次数

为什么用单调栈做？因为找出来的是子序列

如果去掉counter的代码， 会造成使得每个字母只出现一次的条件失效，即有的字母出现0次
counter的作用是在删字母的时候，判断是否会导致有的字母不出现

class Solution:
    def removeDuplicateLetters(self, s) -> int:
        stack = []
        counter = collections.Counter(s)
        for c in s:
            # 要求去重
            if c not in stack:
                # stack[-1] > c | 【严格单调递增】条件被破坏 
                # 需满足 counter[stack[-1]] > 0 的条件，即栈顶元素pop之后，还有替代的
                while stack and (not stack[-1] < c) and counter[stack[-1]] > 0:
                    stack.pop()
                stack.append(c)
            # 遍历一个字符，做更新
            counter[c] -= 1
        return "".join(stack)

TODO: 理解还不深刻， 继续理解

在上一题中，限值条件是k（所以出现在上一题的while判断条件中），这一题的限值条件是使得每个字母只出现一次，故判断条件是counter[stack[-1]]。

counter 表示当前指针及之后所含元素的计数。如果从栈中弹出了元素，并且这个元素后续没有机会再添加进来了，这一定是非法的。

把 counter[mono_stack.back()] 写成了 counter[c] ，人没了

5.1.6 股票价格跨度

901. 股票价格跨度

class StockSpanner:

    def __init__(self):
        # 维护一个【单调递减】栈
        self.stack = []

    def next(self, price: int) -> int:
        cnt = 1
        #                   不满足 单调递减 
        while self.stack and (not self.stack[-1][0] > price):
            top = self.stack.pop()
            cnt += top[1]
        self.stack.append([price, cnt])
        return cnt

5.2 单调队列

5.2.1 队列的最大值

剑指 Offer 59 - II. 队列的最大值

class MaxQueue:

    def __init__(self):
        self.queue = collections.deque()
        # monotonous queue
        self.monoq = collections.deque()


    def max_value(self) -> int:
        return self.monoq[0] if self.monoq else -1


    def push_back(self, value: int) -> None:
        # 单调递减队列 (前一个元素大于等于后一个元素)
        # fixme: 老是把if 写成 while
        while self.monoq and self.monoq[-1] < value:
            self.monoq.pop()
        self.monoq.append(value)
        self.queue.append(value)


    def pop_front(self) -> int:
        if not self.queue:
            return -1
        left = self.queue.popleft()
        if self.monoq[0] == left:
            self.monoq.popleft()
        return left

5.2.2 滑动窗口最大值

239. 滑动窗口最大值

剑指 Offer 59 - I. 滑动窗口的最大值

  • 题解

labuladong 单调队列解题详解

【Python】 简洁的单调队列解法（详解+注释）

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        queue = collections.deque()
        N = len(nums)
        res = []
        for i in range(N):
            # 满足单调递减
            while queue and nums[queue[-1]] < nums[i]:
                queue.pop()  # 默认右端出栈
            queue.append(i)
            # 删掉左端不在滑动窗口内元素
            if queue[0] <= i - k:
                queue.popleft()
            # 如果窗口已经形成，记录结果
            if i >= k - 1:
                # 结果记录的是最大值，所以需要把索引带入nums (默写出错)
                res.append(nums[queue[0]])
        return res

6 栈与队列的相互转换

6.1 两个栈实现队列

剑指 Offer 09. 用两个栈实现队列

入队，直接push到stack1中即可

stack1:
-------------
| 1 2 3 4 
-------------

出队，如果stack2为空，将stack1全部倒腾到stack2中，然后取stack2的栈顶

stack1:
-------------
| 
-------------
stack2:
-------------
    1 2 3 4 | (原来的栈顶变成栈底)
-------------

class CQueue:

    def __init__(self):
        self.stack1 = []
        self.stack2 = []


    def appendTail(self, value: int) -> None:
        self.stack1.append(value)


    def deleteHead(self) -> int:
        if not self.stack2:
            while self.stack1:
                self.stack2.append(self.stack1.pop())
        if self.stack2:
            return self.stack2.pop()
        return -1

6.2 队列实现栈

225. 用队列实现栈

class MyStack {
    Queue<Integer> queue;

    /** Initialize your data structure here. */
    public MyStack() {
        queue=new LinkedList<>();
    }

    /** Push element x onto stack. */
    public void push(int x) {
        int n = queue.size();
        queue.offer(x);
        for (int i = 0; i < n; i++) {
            queue.offer(queue.poll());
        }
    }

    /** Removes the element on top of the stack and returns that element. */
    public int pop() {
        return queue.poll();
    }

    /** Get the top element. */
    public int top() {
        return queue.peek();
    }

    /** Returns whether the stack is empty. */
    public boolean empty() {
        return queue.isEmpty();
    }
}


/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack obj = new MyStack();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.top();
 * boolean param_4 = obj.empty();
 */

你可能感兴趣的:(科学刷题,算法,leetcode,python)

  • 机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习python
    一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
  • 理解Gunicorn：Python WSGI服务器的基石 范范0825 ipythonlinux运维
    理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
  • Cell Insight | 单细胞测序技术又一新发现，可用于HIV-1和Mtb共感染个体诊断 尐尐呅
    结核病是艾滋病合并其他疾病中导致患者死亡的主要原因。其中结核病由结核分枝杆菌（Mycobacteriumtuberculosis,Mtb）感染引起，获得性免疫缺陷综合症（艾滋病）由人免疫缺陷病毒（Humanimmunodeficiencyvirustype1,HIV-1）感染引起。国家感染性疾病临床医学研究中心/深圳市第三人民医院张国良团队携手深圳华大生命科学研究院吴靓团队，共同研究得出单细胞测序
  • 回溯 Leetcode 332 重新安排行程 mmaerd Leetcode刷题学习记录leetcode算法职场和发展
    重新安排行程Leetcode332学习记录自代码随想录给你一份航线列表tickets，其中tickets[i]=[fromi,toi]表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。所有这些机票都属于一个从JFK（肯尼迪国际机场）出发的先生，所以该行程必须从JFK开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。例如，行程[“JFK”,“LGA”]与[“JFK”,“LGB
  • Python数据分析与可视化实战指南 William数据分析 pythonpython数据
    在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
  • 2022-07-08 保利学府里李楚怡1307022
    ——保利碧桂园学府里——童梦奇趣【科学实验室】「7.9-7.10」✏玩出大智慧约99-144㎡二期全新升级力作
  • python os.environ 江湖偌大 python深度学习
    os.environ['TF_CPP_MIN_LOG_LEVEL']='0'#默认值，输出所有信息os.environ['TF_CPP_MIN_LOG_LEVEL']='1'#屏蔽通知信息（INFO）os.environ['TF_CPP_MIN_LOG_LEVEL']='2'#屏蔽通知信息和警告信息（INFO\WARNING）os.environ['TF_CPP_MIN_LOG_LEVEL']='
  • Python中os.environ基本介绍及使用方法 鹤冲天Pro #Pythonpython服务器开发语言
    文章目录python中os.environos.environ简介os.environ进行环境变量的增删改查python中os.environ的使用详解1.简介2.key字段详解2.1常见key字段3.os.environ.get()用法4.环境变量的增删改查和判断是否存在4.1新增环境变量4.2更新环境变量4.3获取环境变量4.4删除环境变量4.5判断环境变量是否存在python中os.envi
  • Pyecharts数据可视化大屏：打造沉浸式数据分析体验 我的运维人生 信息可视化数据分析数据挖掘运维开发技术共享
    Pyecharts数据可视化大屏：打造沉浸式数据分析体验在当今这个数据驱动的时代，如何将海量数据以直观、生动的方式展现出来，成为了数据分析师和企业决策者关注的焦点。Pyecharts，作为一款基于Python的开源数据可视化库，凭借其丰富的图表类型、灵活的配置选项以及高度的定制化能力，成为了构建数据可视化大屏的理想选择。本文将深入探讨如何利用Pyecharts打造数据可视化大屏，并通过实际代码案例
  • Goolge earth studio 进阶4——路径修改与平滑 陟彼高冈yu Googleearthstudio进阶教程旅游
    如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径，所以当我们通过这个关键帧时，不是一个生硬的角度，而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄，允许我们调整路径的形状。右键单击，我们可以选择“平滑路径”，这是默认的自动平滑算法，或者我们可
  • Python教程：一文了解使用Python处理XPath 旦莫 Python进阶python开发语言
    目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath？2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
  • python os.environ_python os.environ 读取和设置环境变量 weixin_39605414 pythonos.environ
    >>>importos>>>os.environ.keys()['LC_NUMERIC','GOPATH','GOROOT','GOBIN','LESSOPEN','SSH_CLIENT','LOGNAME','USER','HOME','LC_PAPER','PATH','DISPLAY','LANG','TERM','SHELL','J2REDIR','LC_MONETARY','QT_QPA
  • 基于社交网络算法优化的二维最大熵图像分割 智能算法研学社（Jack旭） 智能优化算法应用图像分割算法php开发语言
    智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果：5.参考文献：6.Matlab代码摘要：本文介绍基于最大熵的图像分割，并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前，请阅读《图像分割：直方图区域划分及信息统计介绍》htt
  • 509. 斐波那契数(每日一题) lzyprime
    lzyprime博客(github)创建时间：2021.01.04qq及邮箱：2383518170leetcode笔记题目描述斐波那契数，通常用F(n)表示，形成的序列称为斐波那契数列。该数列由0和1开始，后面的每一项数字都是前面两项数字的和。也就是：F(0)=0，F(1)=1F(n)=F(n-1)+F(n-2)，其中n>1给你n，请计算F(n)。示例1：输入：2输出：1解释：F(2)=F(1)+
  • 【华为OD机试真题2023B卷 JAVA&JS】We Are A Team 若博豆 java算法华为javascript
    华为OD2023（B卷）机试题库全覆盖，刷题指南点这里WeAreATeam时间限制：1秒|内存限制：32768K|语言限制：不限题目描述：总共有n个人在机房，每个人有一个标号（1<=标号<=n），他们分成了多个团队，需要你根据收到的m条消息判定指定的两个人是否在一个团队中，具体的：1、消息构成为：abc，整数a、b分别代
  • 使用Faiss进行高效相似度搜索 llzwxh888 faisspython
    在现代AI应用中，快速和高效的相似度搜索是至关重要的。Faiss（FacebookAISimilaritySearch）是一个专门用于快速相似度搜索和聚类的库，特别适用于高维向量。本文将介绍如何使用Faiss来进行相似度搜索，并结合Python代码演示其基本用法。什么是Faiss？Faiss是一个由FacebookAIResearch团队开发的开源库，主要用于高维向量的相似性搜索和聚类。Faiss
  • python是什么意思中文-在python中%是什么意思 编程大乐趣
    Python中%有两种：1、数值运算：%代表取模，返回除法的余数。如：>>>7%212、%操作符（字符串格式化，stringformatting），说明如下：%[(name)][flags][width].[precision]typecode(name)为命名flags可以有+，-，''或0。+表示右对齐。-表示左对齐。''为一个空格，表示在正数的左侧填充一个空格，从而与负数对齐。0表示使用0填
  • Day1笔记-Python简介&标识符和关键字&输入输出 ~在杰难逃~ Pythonpython开发语言大数据数据分析数据挖掘
    大家好，从今天开始呢，杰哥开展一个新的专栏，当然，数据分析部分也会不定时更新的，这个新的专栏主要是讲解一些Python的基础语法和知识，帮助0基础的小伙伴入门和学习Python，感兴趣的小伙伴可以开始认真学习啦！一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码，再通过语言处理程序执行向计算机发送指令，让计算机完成对应的工作，编程
  • python八股文面试题分享及解析(1) Shawn________ python
    #1.'''a=1b=2不用中间变量交换a和b'''#1.a=1b=2a,b=b,aprint(a)print(b)结果：21#2.ll=[]foriinrange(3):ll.append({'num':i})print(11)结果:#[{'num':0},{'num':1},{'num':2}]#3.kk=[]a={'num':0}foriinrange(3):#0,12#可变类型，不仅仅改变
  • 121. 买卖股票的最佳时机 薄荷糖的味道_fb40
    给定一个数组，它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天（股票价格=1）的时候买入，在第5天（股票价格=6）的时候卖出，最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
  • 每日算法&面试题，大厂特训二十八天——第二十天（树） 肥学 ⚡算法题⚡面试题每日精进java算法数据结构
    目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
  • Python快速入门 —— 第三节：类与对象 孤华暗香 Python快速入门python开发语言
    第三节：类与对象目标：了解面向对象编程的基础概念，并学会如何定义类和创建对象。内容：类与对象：定义类：class关键字。类的构造函数：__init__()。类的属性和方法。对象的创建与使用。示例：classStudent:def__init__(self,name,age,major):self.name&#
  • 人怎么才能认识自己？ 阿尚青子自由写作人
    人怎么才能认识自己？（原问题）我从不愿意上纲上线地确定偌大的话题，就直接说吧。纵使你能认识世界上的万事万物，你很难做到真实地认识自己。因为即使就这个世界，基本上每个人也很难做到客观、公正、科学地认识。对你好的人就是好吗？一件事情是否能够保持永远原来的样子？借不到钱的男友，女友想离开他就理直气壮？父母对子女有几分慷慨，又有几分是无私？工作的意义究竟是什么？是工作需要你，还是你需要工作呢？诸如此类的问
  • pyecharts——绘制柱形图折线图 2224070247 信息可视化pythonjava数据可视化
    一、pyecharts概述自2013年6月百度EFE(ExcellentFrontEnd）数据可视化团队研发的ECharts1.0发布到GitHub网站以来，ECharts一直备受业界权威的关注并获得广泛好评，成为目前成熟且流行的数据可视化图表工具，被应用到诸多数据可视化的开发领域。Python作为数据分析领域最受欢迎的语言，也加入ECharts的使用行列，并研发出方便Python开发者使用的数据
  • 回溯算法-重新安排行程 chirou_ 算法数据结构图论c++图搜索
    leetcode332.重新安排行程这题我还没自己ac过，只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多，用什么数据结构去存数据，去读取数据，都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
  • Python 实现图片裁剪（附代码） | Python工具 剑客阿良_ALiang
    前言本文提供将图片按照自定义尺寸进行裁剪的工具方法，一如既往的实用主义。环境依赖ffmpeg环境安装，可以参考我的另一篇文章：windowsffmpeg安装部署_阿良的博客-CSDN博客本文主要使用到的不是ffmpeg，而是ffprobe也在上面这篇文章中的zip包中。ffmpy安装：pipinstallffmpy-ihttps://pypi.douban.com/simple代码不废话了，上代码
  • 【华为OD技术面试真题 - 技术面】- python八股文真题题库（4) 算法大师 华为od面试python
    华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选**1.Python中的`with`**用途和功能自动资源管理示例：文件操作上下文管理协议示例代码工作流程解析优点2.\_\_new\_\_和**\_\_init\_\_**区别__new____init__区别总结3.**切片（Slicing）操作**基本切片语法
  • python os 环境变量 CV矿工 python开发语言numpy
    环境变量：环境变量是程序和操作系统之间的通信方式。有些字符不宜明文写进代码里，比如数据库密码，个人账户密码，如果写进自己本机的环境变量里，程序用的时候通过os.environ.get（）取出来就行了。os.environ是一个环境变量的字典。环境变量的相关操作importos"""设置/修改环境变量：os.environ[‘环境变量名称’]=‘环境变量值’#其中key和value均为string类
  • Python爬虫解析工具之xpath使用详解 eqa11 python爬虫开发语言
    文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中，数据提取是一个至关重要的环节。xpath作为一门
  • C++ | Leetcode C++题解之第409题最长回文串 Ddddddd_158 经验分享C++Leetcode题解
    题目：题解：classSolution{public:intlongestPalindrome(strings){unordered_mapcount;intans=0;for(charc:s)++count[c];for(autop:count){intv=p.second;ans+=v/2*2;if(v%2==1andans%2==0)++ans;}returnans;}};
  • Linux的Initrd机制 被触发 linux
    Linux 的 initrd 技术是一个非常普遍使用的机制，linux2.6 内核的 initrd 的文件格式由原来的文件系统镜像文件转变成了 cpio 格式，变化不仅反映在文件格式上， linux 内核对这两种格式的 initrd 的处理有着截然的不同。本文首先介绍了什么是 initrd 技术，然后分别介绍了 Linux2.4 内核和 2.6 内核的 initrd 的处理流程。最后通过对 Lin
  • maven本地仓库路径修改 bitcarter maven
    默认maven本地仓库路径：C:\Users\Administrator\.m2 修改maven本地仓库路径方法：     1.打开E:\maven\apache-maven-2.2.1\conf\settings.xml     2.找到        
  • XSD和XML中的命名空间 darrenzhu xmlxsdschemanamespace命名空间
    http://www.360doc.com/content/12/0418/10/9437165_204585479.shtml http://blog.csdn.net/wanghuan203/article/details/9203621 http://blog.csdn.net/wanghuan203/article/details/9204337 http://www.cn
  • Java 求素数运算 周凡杨 java算法素数
    网络上对求素数之解数不胜数，我在此总结归纳一下，同时对一些编码，加以改进，效率有成倍热提高。 第一种：   原理: 6N(+-)1法         任何一个自然数，总可以表示成为如下的形式之一： 6N，6N+1，6N+2，6N+3，6N+4，6N+5 (N=0，1，2，…)   
  • java 单例模式 g21121 java
    想必单例模式大家都不会陌生，有如下两种方式来实现单例模式：   class Singleton { private static Singleton instance=new Singleton(); private Singleton(){} static Singleton getInstance() { return instance; }
  • Linux下Mysql源码安装 510888780 mysql
    1.假设已经有mysql-5.6.23-linux-glibc2.5-x86_64.tar.gz (1)创建mysql的安装目录及数据库存放目录       解压缩下载的源码包，目录结构，特殊指定的目录除外：           
  • 32位和64位操作系统 墙头上一根草 32位和64位操作系统
    32位和64位操作系统是指：CPU一次处理数据的能力是32位还是64位。现在市场上的CPU一般都是64位的，但是这些CPU并不是真正意义上的64 位CPU，里面依然保留了大部分32位的技术，只是进行了部分64位的改进。32位和64位的区别还涉及了内存的寻址方面，32位系统的最大寻址空间是2 的32次方= 4294967296（bit）= 4（GB）左右，而64位系统的最大寻址空间的寻址空间则达到了
  • 我的spring学习笔记10-轻量级_Spring框架 aijuans Spring 3
    一、问题提问：     → 请简单介绍一下什么是轻量级？     轻量级（Leightweight）是相对于一些重量级的容器来说的，比如Spring的核心是一个轻量级的容器，Spring的核心包在文件容量上只有不到1M大小，使用Spring核心包所需要的资源也是很少的，您甚至可以在小型设备中使用Spring。  
  • mongodb 环境搭建及简单CURD antlove WebInstallcurdNoSQLmongo
    一 搭建mongodb环境 1. 在mongo官网下载mongodb 2. 在本地创建目录 "D:\Program Files\mongodb-win32-i386-2.6.4\data\db" 3. 运行mongodb服务 [mongod.exe --dbpath "D:\Program Files\mongodb-win32-i386-2.6.4\data\
  • 数据字典和动态视图 百合不是茶 oracle数据字典动态视图系统和对象权限
    数据字典（data dictionary）是 Oracle 数据库的一个重要组成部分，这是一组用于记录数据库信息的只读（read-only）表。随着数据库的启动而启动,数据库关闭时数据字典也关闭   数据字典中包含   数据库中所有方案对象（schema object）的定义(包括表，视图，索引，簇，同义词，序列，过程，函数，包，触发器等等) 数据库为一
  • 多线程编程一般规则 bijian1013 javathread多线程java多线程
           如果两个工两个以上的线程都修改一个对象，那么把执行修改的方法定义为被同步的，如果对象更新影响到只读方法，那么只读方法也要定义成同步的。        不要滥用同步。如果在一个对象内的不同的方法访问的不是同一个数据，就不要将方法设置为synchronized的。
  • 将文件或目录拷贝到另一个Linux系统的命令scp bijian1013 linuxunixscp
    一.功能说明        scp就是security copy，用于将文件或者目录从一个Linux系统拷贝到另一个Linux系统下。scp传输数据用的是SSH协议，保证了数据传输的安全，其格式如下：        scp 远程用户名@IP地址：文件的绝对路径
  • 【持久化框架MyBatis3五】MyBatis3一对多关联查询 bit1129 Mybatis3
    以教员和课程为例介绍一对多关联关系，在这里认为一个教员可以叫多门课程，而一门课程只有1个教员教，这种关系在实际中不太常见，通过教员和课程是多对多的关系。   示例数据：   地址表：   CREATE TABLE ADDRESSES ( ADDR_ID INT(11) NOT NULL AUTO_INCREMENT, STREET VAR
  • cookie状态判断引发的查找问题 bitcarter formcgi
    先说一下我们的业务背景： 1.前台将图片和文本通过form表单提交到后台，图片我们都做了base64的编码，并且前台图片进行了压缩 2.form中action是一个cgi服务 3.后台cgi服务同时供PC，H5，APP 4.后台cgi中调用公共的cookie状态判断方法（公共的，大家都用，几年了没有问题） 问题：（折腾两天。。。。） 1.PC端cgi服务正常调用，cookie判断没
  • 通过Nginx,Tomcat访问日志(access log)记录请求耗时 ronin47
    一、Nginx通过$upstream_response_time $request_time统计请求和后台服务响应时间 nginx.conf使用配置方式： log_format main '$remote_addr - $remote_user [$time_local] "$request" ''$status $body_bytes_sent "$http_r
  • java-67- n个骰子的点数。 把n个骰子扔在地上，所有骰子朝上一面的点数之和为S。输入n，打印出S的所有可能的值出现的概率。 bylijinnan java
    public class ProbabilityOfDice { /** * Q67 n个骰子的点数 * 把n个骰子扔在地上，所有骰子朝上一面的点数之和为S。输入n，打印出S的所有可能的值出现的概率。 * 在以下求解过程中，我们把骰子看作是有序的。 * 例如当n=2时，我们认为（1，2）和（2，1）是两种不同的情况 */ private stati
  • 看别人的博客，觉得心情很好 Cb123456 博客心情
       以为写博客，就是总结，就和日记一样吧，同时也在督促自己。今天看了好长时间博客:    职业规划:    http://www.iteye.com/blogs/subjects/zhiyeguihua      android学习:    1.http://byandby.i
  • [JWFD开源工作流]尝试用原生代码引擎实现循环反馈拓扑分析 comsci 工作流
        我们已经不满足于仅仅跳跃一次，通过对引擎的升级，今天我测试了一下循环反馈模式，大概跑了200圈，引擎报一个溢出错误      在一个流程图的结束节点中嵌入一段方程，每次引擎运行到这个节点的时候，通过实时编译器GM模块，计算这个方程，计算结果与预设值进行比较，符合条件则跳跃到开始节点，继续新一轮拓扑分析，直到遇到
  • JS常用的事件及方法 cwqcwqmax9 js
    事件 描述 onactivate 当对象设置为活动元素时触发。 onafterupdate 当成功更新数据源对象中的关联对象后在数据绑定对象上触发。 onbeforeactivate 对象要被设置为当前元素前立即触发。 onbeforecut 当选中区从文档中删除之前在源对象触发。 onbeforedeactivate 在 activeElement 从当前对象变为父文档其它对象之前立即
  • 正则表达式验证日期格式 dashuaifu 正则表达式IT其它java其它
    正则表达式验证日期格式 function isDate(d){ var v = d.match(/^(\d{4})-(\d{1,2})-(\d{1,2})$/i); if(!v) { this.focus(); return false; } } <input value="2000-8-8" onblu
  • Yii CModel.rules() 方法 、validate预定义完整列表、以及说说验证 dcj3sjt126com yii
    public array rules () {return} array 要调用 validate() 时应用的有效性规则。 返回属性的有效性规则。声明验证规则，应重写此方法。 每个规则是数组具有以下结构：array('attribute list', 'validator name', 'on'=>'scenario name', ...validation
  • UITextAttributeTextColor = deprecated in iOS 7.0 dcj3sjt126com ios
    In this lesson we used the key "UITextAttributeTextColor" to change the color of the UINavigationBar appearance to white. This prompts a warning "first deprecated in iOS 7.0." Ins
  • 判断一个数是质数的几种方法 EmmaZhao Mathpython
    质数也叫素数，是只能被1和它本身整除的正整数，最小的质数是2，目前发现的最大的质数是p=2^57885161-1【注1】。 判断一个数是质数的最简单的方法如下： def isPrime1(n): for i in range(2, n): if n % i == 0: return False return True 但是在上面的方法中有一些冗余的计算，所以
  • SpringSecurity工作原理小解读 坏我一锅粥 SpringSecurity
      SecurityContextPersistenceFilter   ConcurrentSessionFilter   WebAsyncManagerIntegrationFilter   HeaderWriterFilter   CsrfFilter   LogoutFilter   Use
  • JS实现自适应宽度的Tag切换 ini JavaScripthtmlWebcsshtml5
    效果体验：http://hovertree.com/texiao/js/3.htm   该效果使用纯JavaScript代码，实现TAB页切换效果，TAB标签根据内容自适应宽度，点击TAB标签切换内容页。 HTML文件代码： <!DOCTYPE html> <html xmlns="http://www.w3.org/1999/xhtml"
  • Hbase Rest API : 数据查询 kane_xie RESThbase
    hbase（hadoop）是用java编写的，有些语言（例如python）能够对它提供良好的支持，但也有很多语言使用起来并不是那么方便，比如c#只能通过thrift访问。Rest就能很好的解决这个问题。Hbase的org.apache.hadoop.hbase.rest包提供了rest接口，它内嵌了jetty作为servlet容器。   启动命令：./bin/hbase rest s
  • JQuery实现鼠标拖动元素移动位置（源码+注释） 明子健 jqueryjs源码拖动鼠标
    欢迎讨论指正！   print.html代码： <!DOCTYPE html> <html> <head> <meta http-equiv=Content-Type content="text/html;charset=utf-8"> <title>发票打印</title> &l
  • Postgresql 连表更新字段语法 update qifeifei PostgreSQL
    下面这段sql本来目的是想更新条件下的数据，可是这段sql却更新了整个表的数据。sql如下： UPDATE tops_visa.visa_order SET op_audit_abort_pass_date = now() FROM tops_visa.visa_order as t1 INNER JOIN tops_visa.visa_visitor as t2 ON t1.
  • 将redis,memcache结合使用的方案? tcrct rediscache
    公司架构上使用了阿里云的服务，由于阿里的kvstore收费相当高，打算自建，自建后就需要自己维护，所以就有了一个想法，针对kvstore(redis)及ocs(memcache)的特点，想自己开发一个cache层，将需要用到list，set，map等redis方法的继续使用redis来完成，将整条记录放在memcache下，即findbyid，save等时就memcache，其它就对应使用redi
  • 开发中遇到的诡异的bug wudixiaotie bug
    今天我们服务器组遇到个问题： 我们的服务是从Kafka里面取出数据，然后把offset存储到ssdb中，每个topic和partition都对应ssdb中不同的key，服务启动之后，每次kafka数据更新我们这边收到消息，然后存储之后就发现ssdb的值偶尔是-2,这就奇怪了，最开始我们是在代码中打印存储的日志，发现没什么问题，后来去查看ssdb的日志，才发现里面每次set的时候都会对同一个key
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他