机器学习——自然语言处理（NLP）一

机器学习——自然语言处理（NLP）一

---

前言

自然语言处理（Natural Language Processing，NLP）是一门研究如何使计算机能够理解和处理人类语言的学科，其中有许多常用的算法和技术，本文则主要介绍比较基础的TF-IDF算法和朴素贝叶斯算法。

---

一、TF-IDF算法

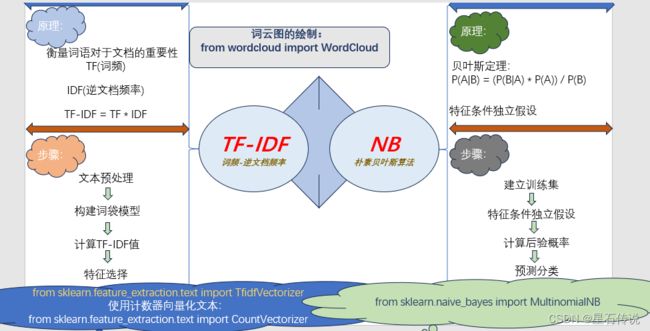
1.1. 原理

一种用于评估一个词语对于一个文件集或一个语料库的重要程度的统计方法。 可以参与文本分类、文本相似度计算、信息检索等任务。（TF-IDF算法本身并不是一个分类算法，只是用于将文本数据转换为可供分类算法使用的特征表示）
它通过计算一个词语在文档中的出现频率（TF)和在整个语料库中的出现频率的比值，来衡量该词语对于文档的重要性。

1. TF（词频）表示一个词语在文档中出现的频率，计算公式为：
   TF = (词语在文档中出现的次数) / (文档中的总词语数)。

2. IDF（逆文档频率）表示一个词语在整个语料库中的出现频率的倒数，计算公式为：
   IDF = log((语料库中的文档总数) / (包含该词语的文档数 + 1))。

3. TF-IDF的计算公式为：
   TF-IDF = TF * IDF。

1.2. 算法步骤：

1.2.1. 文本预处理

文本预处理： 在应用TF-IDF算法之前，需要对文本进行预处理，包括去除标点符号、停用词等。

1. 删除停用词：去除常见的无实际含义的词语，它们通常无法告诉你关于文档的内容，如“a”、“is”、“the”等。

2. 去除标点符号：使用正则表达式或字符串操作函数去除文本中的标点符号

3. 词干提取/还原：如一个单词有多种形式（过去时、现代时等等），可以合并为一种形式

4. 分词：将文本分割成单个的词语或标记，可以使用空格或其他分隔符进行分词
   …

1.2.2. 构建词袋模型

构建词袋模型：将预处理后的文本转换为词袋（BOW）的表现形式，即向量化文本，创建词条-文档矩阵，矩阵的每一列表示一个词语，而每个文档对应于每一行，两者的交点是该词语在文本中出现的次数。

1.2.3. 计算TF-IDF值

计算TF-IDF值：将TF和IDF相乘，得到每个词语的TF-IDF值。TF-IDF值越大，表示词语在文本中越重要

1.2.4. 特征选择

根据设定的阈值或其他规则，选择具有较高TF-IDF值的词语作为特征词，

因为由tf-idf值的计算公式可知，为了获得较高的tf-idf值，一个词条需要在较少的文档中出现较高的次数，这样我们就可认为文档由具有较高tf-idf值的词条所表示

1.3. 代码实现

数据集为sklearn库中的新闻组数据集（fetch_20newsgroups）

1.3.1. TF-IDF

TfidfVectorizer(ngram_range= , stop_words= , min_df= )

1. ngram_range：表示文档是如何被分词的。以文档" This is stone" 为例，ngram_range=(1, 3)表示提取单个词、相邻两个词、相邻三个词的组合，即 ”This"、“This is”、“This is stone"、“is”、“is stone” 和 “stone”

这样进行分词，能将观察单词与单词之间的关系的窗口扩大，帮助算法更好理解文本。

2. stop_words ：删除指定的停用词，例如 stop_words=“english”，表示删除所有的英语停用词

3. mid_df：这里会删除所有文档频率小于指定数的单词，可移除那些极其罕见的词条来减小矩阵规模。

from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import accuracy_score
import pandas as pd
# 加载新闻组数据集
newsgroups_train = fetch_20newsgroups(subset='train')
newsgroups_test = fetch_20newsgroups(subset='test')
data_train = newsgroups_train.data
target_train = newsgroups_train.target
data_test = newsgroups_test.data
target_test = newsgroups_test.target
# df_train = pd.DataFrame(data= np.c_[newsgroups_train.data,newsgroups_train.target],columns= ["text","target"])
# df_train.to_csv("newsgroups_train.csv")
# df_test = pd.DataFrame(data= np.c_[newsgroups_test.data,newsgroups_test.target],columns= ["text","target"])
# df_test.to_csv("newsgroups_test.csv")


# 创建TF-IDF向量化器
vectorizer = TfidfVectorizer(stop_words="english", min_df=3)


# 对训练集和测试集进行向量化
data_train_tfidf = vectorizer.fit_transform(data_train)
data_test_tfidf = vectorizer.transform(data_test)

#整合为数据框形式
df = pd.DataFrame(
    data= data_train_tfidf.toarray(),
    columns = vectorizer.get_feature_names()
)

1.3.2 计数器向量化文本

from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer(stop_words="english",min_df= 3)
data_train_tfidf = vectorizer.fit_transform(data_train)
data_test_tfidf = vectorizer.transform(data_test)

1.3.3. 两者的区别

1. 计数器向量化文本只考虑了词频，而TF-IDF算法向量化文本同时考虑了词频和词的重要性，给常见词较低的权重，给罕见词较高的权重。

2. 计数器向量化文本没有对常见词进行特殊处理，而TF-IDF算法向量化文本通过逆文档频率来减小常见词的权重，提高罕见词的权重。

3. 总之，计数器向量化文本适用于简单的文本分类任务，TF-IDF算法适用于更复杂的文本处理任务。

1.3.4. 绘制简单的词云图（额外）

#简单的对一个文档进行词云图绘制
data_train_ciyu =[data_train[0]]
#print(data_train_ciyu)
vectorizer = TfidfVectorizer( stop_words="english")
tfidf_matrix = vectorizer.fit_transform(data_train_ciyu)

# 获取词条列表
feature_names = vectorizer.get_feature_names()

# 获取每个词条的TF-IDF值
tfidf_values = tfidf_matrix.toarray()[0]
df = pd.DataFrame(
    data= tfidf_matrix.toarray(),
    columns = vectorizer.get_feature_names()
)
print(df)
         15       60s       70s  ...       wam  wondering     years
0  0.104828  0.104828  0.104828  ...  0.209657   0.104828  0.104828


# 创建一个字典，将词条和对应的TF-IDF值存储起来
word_tfidf_dict = dict(zip(feature_names, tfidf_values))
# 按TF-IDF值降序排序
sorted_words = sorted(word_tfidf_dict.items(), key=lambda x: x[1], reverse=True)
#print(sorted_words)

from wordcloud import WordCloud
# 获取文档频率最高的词条
top_words = dict(sorted_words[:10])
print(top_words)
{'car': 0.5241424183609592, 'edu': 0.20965696734438366, 'lerxst': 0.20965696734438366, 'umd': 0.20965696734438366, 'wam': 0.20965696734438366, '15': 0.10482848367219183, '60s': 0.10482848367219183, '70s': 0.10482848367219183, 'addition': 0.10482848367219183, 'body': 0.10482848367219183}

# 创建词云对象
wordcloud = WordCloud()

# 生成词云图
wordcloud.generate_from_frequencies(top_words)

# 绘制词云图
plt.imshow(wordcloud, interpolation='bilinear')
plt.axis("off")
plt.show()

从该图中可看出car这个单词出现频率最高，故可推断该文档应该与汽车有关，（事实上确实是讲述汽车的新闻），原文档如下图所示：

这个词云图的绘制还是相当粗糙的，一般情况下是要根据自己的要求来对文档中单词的读取进行一定的选择（比如，去掉无实际意义的数字，字符等等），还有许多别的什么操作等等。这样才能绘制满足自己要求的精致的词云图。

二、朴素贝叶斯算法

2.1. 原理

朴素贝叶斯算法是基于贝叶斯定理与特征条件独立假设的分类方法（“朴素”，指的就是特征条件独立），
对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率（即求条件概率），然后综合这些概率对其所在的特征向量做出分类预测（哪个最大，就认为此待分类项属于哪个类别）

贝叶斯定理是概率论中的重要定理，用于计算在已知一些先验信息的情况下，根据新的观测数据来更新对事件的概率估计。

对于事件 A 和事件 B，贝叶斯定理可以表示为：

P(A|B) = (P(B|A) * P(A)) / P(B)

表示事件B已经发生的前提下，事件A发生的概率（即事件B发生下事件A的条件概率）

2.2. 算法步骤

当观察到输入样本X时，其属于类别C的概率值为：P(C|X) = P(X|C) * P( C ) / P(X)

朴素贝叶斯算法的核心思想是基于贝叶斯定理来计算后验概率P(C|X)，并选择具有最大后验概率的类别作为预测结果。对于给定的输入样本X，朴素贝叶斯算法通过以下步骤进行分类：

1. 建立训练集：从已标记的数据集中，统计每个类别的先验概率 P( C)（类别 A中的样本数除以总样本数）以及每个特征在各个类别条件下的条件概率 P(X|C)（表示在类别 C下特征 X 出现的概率）。

2. 特征条件独立性假设：朴素贝叶斯算法假设所有特征之间相互独立。即对于给定的类别 C 和特征集合 X={x₁, x₂, …, xₙ}，条件概率可以表示为 P(X|C) = P(x₁|C) * P(x₂|C) * … * P(xₙ|C)。

3. 计算后验概率：对于每个类别 C，计算后验概率 P(C|X) = P(X|C) * P(C )，其中 P(X|C) 表示在类别 C 下特征 X 出现的概率，P(C ) 是先验概率。

4. 预测分类：选择具有最大后验概率的类别作为预测结果。即找到 max P(C|X)。

2.3. 代码实现

alpha是一个平滑参数，越小越易过拟合，反之则欠拟合

from sklearn.naive_bayes import MultinomialNB
model = MultinomialNB(alpha= 0.001) 
model.fit(data_train_tfidf,target_train)
print(model.score(data_test_tfidf,target_test))
print(model.score(data_train_tfidf,target_train))
#结果：
0.8199681359532661
0.9953155382711685



#使用网格搜索
import numpy as np
from sklearn.model_selection import GridSearchCV
params = {
    "alpha": np.linspace(0.00001,0.01,100),
    "fit_prior": [True,False],
}
grid_search = GridSearchCV(MultinomialNB(),param_grid= params,cv= 5)
grid_search.fit(data_train_tfidf,target_train)
best_NB = grid_search.best_estimator_
print(best_NB)
print(grid_search.best_score_)
print(grid_search.best_params_)
best_NB.fit(data_train_tfidf,target_train)
# 在测试集上进行预测
y_pred = best_NB.predict(data_test_tfidf)
# 计算准确率
accuracy = accuracy_score(target_test, y_pred)
print('Accuracy:', accuracy)

#结果：
MultinomialNB(alpha=0.007880909090909091)
0.9106417269627534
{'alpha': 0.007880909090909091, 'fit_prior': True}
Accuracy: 0.830323951141795




#模型的评价
#使用classification_report函数，查看预测结果的准确性
from sklearn.metrics import classification_report
model = best_NB
model.fit(data_train_tfidf, target_train)
pred = model.predict(data_test_tfidf)
#print(pred)
import pprint
pprint.pprint(classification_report(y_true=target_test,y_pred= pred,target_names=newsgroups_test.target_names))

#使用混淆矩阵，观察每种类别被错误分类的情况
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(target_test,pred)
#print(cm)

#混淆矩阵的可视化
import seaborn as sns
sns.heatmap(cm, annot=True, fmt='d', cmap='Reds')
plt.xlabel('Predicted')
plt.ylabel('True')
plt.title('Confusion Matrix')
plt.show()
sns.heatmap(cm, annot=False, fmt='d', cmap='Blues')
plt.xlabel('Predicted')
plt.ylabel('True')
plt.title('Confusion Matrix')
plt.show()

#cmap参数：
"""
'Blues': 蓝色调的渐变色图谱
'Greens': 绿色调的渐变色图谱
'Reds': 红色调的渐变色图谱
'Oranges': 橙色调的渐变色图谱
'coolwarm': 冷暖色调的渐变色图谱
'viridis': 从蓝色到黄色的渐变色图谱
'hot': 火热色调的渐变色图谱
"""

#整合起来
li = list(zip(data_test,pred))
#print(len(li))
#print(len(data_test))
result = pd.DataFrame(data= np.c_[ [ li[x][0] for x in range(len(li))],[li[x][1] for x in range(len(li))]], columns= ["data_test","predict"])
#print(result.head())
result.to_csv("result.csv",index= False)

由此通过朴素贝叶斯算法得到了一个简单的分类模型，我们可以取任意的文本来测试一下分类情况：

print(model)
MultinomialNB(alpha=0.007880909090909091)

documents = ["This new department would become the world's primary research center for computer graphics",
             "The three astronauts of Shenzhou ten return safe space congratulations "
             ]

documents_vector = vectorizer.transform(documents)
model.fit(data_train_tfidf,target_train)
pred = model.predict(documents_vector)
print(pred)
[ 1 14]
#print(list(zip(documents,pred)))

这两个文本分别是介绍计算机图形学和航天的内容，分别是1、14，成功分类。（当然由于模型比较简单的问题，可能会出现许多分类错误问题）
这时，我们就需要不断对算法进行优化和改善了。
或者运用其它分类算法（总之就是为了得到最佳的算法模型）

三、其它分类算法

3.1. 支持向量机

from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV
"""
params = {
    "kernel": ["rbf","sigmoid","poly","linear"],
    "C": np.arange(1,6),
    "gamma": np.arange(0,0.5,0.001),
    "degree":np.arange(1,5)
}
# 创建SVM分类器并进行训练
svm = SVC()
grid_searchcv = GridSearchCV(svm,param_grid= params,cv= 5)
grid_searchcv.fit(data_train_tfidf, target_train)
best_svc = grid_searchcv.best_estimator_
print(best_svc)
best_svc.fit(data_train_tfidf,target_train)
# 在测试集上进行预测
y_pred = best_svc.predict(data_test_tfidf)
print(best_svc.score(target_test,y_pred))
# 计算准确率
accuracy = accuracy_score(target_test, y_pred)
print('Accuracy:', accuracy)
"""

#因为等待时间太过漫长，就不进行网格搜索了，直接创建简单的模型
best_svc= SVC()
best_svc.fit(data_train_tfidf,target_train)
y_pred = best_svc.predict(data_test_tfidf)
# 计算准确率
accuracy = accuracy_score(target_test, y_pred)

print('Accuracy:', accuracy)
Accuracy: 0.8251460435475305

3.2. 随机森林

from sklearn.ensemble import RandomForestClassifier
# 创建随机森林分类器并进行训练
"""
param_grids = {
    "criterion": ["gini","entropy"],
    "max_depth":np.arange(1,10),
    "min_samples_leaf":np.arange(1,10),
    "max_features": np.arange(1,3)
}
rf = RandomForestClassifier()
grid_search = GridSearchCV(rf,param_grid=param_grids,n_jobs= 4,scoring="accuracy",cv=5)
grid_search.fit(data_train_tfidf,target_train)
best_rf = grid_search.best_estimator_
print(grid_search.best_score_)
print(best_rf)
best_rf.fit(data_train_tfidf, target_train)

# 在测试集上进行预测
y_pred = best_rf.predict(data_test_tfidf)

# 计算准确率
accuracy = accuracy_score(target_test, y_pred)
print('Accuracy:', accuracy)
"""


best_rf = RandomForestClassifier()
best_rf.fit(data_train_tfidf, target_train)

# 在测试集上进行预测
y_pred = best_rf.predict(data_test_tfidf)

# 计算准确率
accuracy = accuracy_score(target_test, y_pred)

print('Accuracy:', accuracy)
Accuracy: 0.7716409984067977

四、比较与选择

在进行文档分类时，朴素贝叶斯算法、支持向量机（SVM）和随机森林算法是常用的分类算法之一

1. 朴素贝叶斯算法（Naive Bayes）：

优点：简单、易于实现，对于高维数据和大规模数据集有较好的性能，适用于文本分类等任务。

缺点：朴素贝叶斯算法假设特征之间相互独立，这在实际情况下可能不成立，故在特征相关性较强的情况下，可能表现不佳。

2. 支持向量机：

优点：SVM在处理高维数据和小样本数据时表现较好，具有较强的泛化能力，并且可以处理非线性问题。

缺点：SVM对于大规模数据集的训练时间较长，且对于噪声和缺失数据敏感，需要进行特征缩放和调参。

3. 随机森林算法：

优点：通过多个决策树的投票结果来进行分类，具有较好的准确性和鲁棒性，对于高维数据和缺失数据有较好的处理能力。

缺点：在处理大规模数据集时需要较多的计算资源，且对于高度相关的特征可能表现不佳。

在训练时间和计算资源有限的情况下，朴素贝叶斯算法是一个较快速的选择，若充足，可考虑另外两种算法（只能说相比之下，这两种算法太慢了）

如果特征之间相互独立或相关性较低，朴素贝叶斯算法可能表现较好
如果数据集规模较大或特征维度较低，可以考虑使用支持向量机或随机森林算法，反之特征维度较高则用NB算法
如果对准确性和鲁棒性有较高要求，可以考虑使用随机森林算法

---

总结

本文介绍了自然语言处理中的简单算法，文本向量化的算法：TF-IDF算法以及计数器向量化；文本分类算法：朴素贝叶斯算法以及其它分类算法。最后对这些分类算法进行了一定的比较。

流光容易把人抛， 红了樱桃 ，绿了芭蕉。

–2023-9-7 筑基篇