机器学习——支持向量机（SVM）

机器学习——支持向量机（SVM）

---

前言

支持向量机（SVM）是一种常见的机器学习方法，常用于分类（线性和非线性分类问题），回归问题。本文将详细介绍一下支持向量机算法

---

一、SVM算法原理

1.1. SVM介绍

支持向量机（Support Vector Machine，SVM）是一种常用的机器学习算法，SVM可以用于线性和非线性分类问题，回归以及异常值检测
其基本原理是通过在特征空间中找到一个超平面，将不同类别的样本分开，并且使得离超平面最近的样本点到超平面的距离最大化。

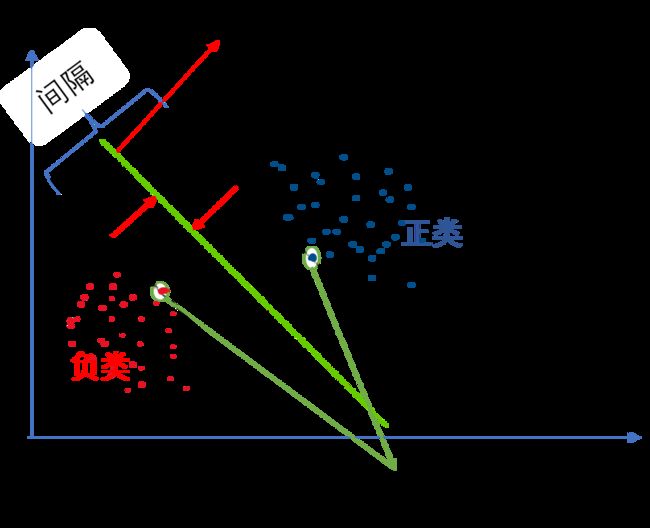
以一个二维平面为例，判定边界是一个超平面（在本图中其实是一条线，但是可以将它想象为一个平面乃至更高维形式在二维平面的映射），它是由支持向量所确定的（支持向量是离判定边界最近的样本点，它们决定了判定边界的位置）。
间隔的正中就是判定边界，间隔距离体现了两类数据的差异大小

若严格地规定所有的样本点都不在“缓冲区”，都正确的在两边，称为硬间隔分类； 但是在一般情况下，不易实现，这里有两个问题：
第一，它只对线性可分的数据起作用。第二，有异常值的干扰。

为了避免这些问题，可使用软间隔分类：
在保持“缓冲区”尽可能大和避免间隔违规之间找到一个良好的平衡，在sklearn中的SVM类，可以使用超参数 C(惩罚系数），控制了模型的复杂度和容错能力。较小的C值会导致容错能力较高（即更宽的缓冲区），可能会产生更多的错误分类（即间隔违规）；较大的C值会导致容错能力较低，可能会产生更少的错误分类。

1.2. 核函数（Kernel）介绍

为什么要引入核函数呢？ 因为在SVM中，有时候很难找出一条线或一个超平面来分割数据集，这时候我们就需要升维（把无法线性分割的样本映射到高纬度空间，在高维空间实现分割）

核函数是特征转换函数，它可以将数据映射到高维特征空间中，从而更好地处理非线性关系。
核函数的作用是通过计算两个样本之间的相似度（内积）来替代显式地进行特征映射，从而避免了高维空间的计算开销。

在SVM中，核函数的选择非常重要，它决定了模型能够学习的函数空间。常见的核函数包括：

1. 线性核函数（Linear Kernel）：最简单的核函数，它在原始特征空间中直接计算内积，适用于线性可分的情况。K(X,y) = (X^T) * y

2. 多项式核函数（Polynomial Kernel）：通过多项式函数将数据映射到高维空间，可以处理一定程度的非线性关系。(可拟合出复杂的分割超平面，但可选参数太多，阶数高后计算困难，不稳定） K(X,y) = ( (X^T) * y + c ) ^ d , 其中 c 为常数，d 为多项式的阶数。

3. 高斯核函数（Gaussian Kernel）：也称为径向基函数（Radial Basis Function，RBF），通过高斯分布将数据映射到无穷维的特征空间，可以处理更复杂的非线性关系。形式为 K(x,y) = exp( -|| x-y || ^2 / (2 σ ^2) ) 。
   || x - y || 表示向量 x 和 y 之间的欧氏距离，即它们各个维度差值的平方和的平方根。
   σ 是高斯核函数的参数，控制了样本之间相似度的衰减速度。σ 越小，样本之间的相似度下降得越快；σ 越大，样本之间的相似度下降得越慢。

4. sigmoid核函数（Sigmoid Kernel）：通过sigmoid函数将数据映射到高维空间，适用于二分类问题。 σ(x) = 1 / (1 + exp(-x))

1.3. 算法和核函数的选择

假设特征数为N，训练数据集的样本个数为W，可按如下规则选择算法：

1. 若N相对W较大，使用逻辑回归或线性核函数的SVM算法

2. 若N较小，W中等大小（W为N的十倍左右），可使用高斯核函数的SVM算法

3. 若N较小，W较大（W为N的五十倍以上），可以使用多项式核函数、高斯核函数的SVM算法

总之 ，数据大的问题，选择复杂一些的模型，反之，选择简单模型。

有关逻辑回归算法的更多信息，请看
机器学习——逻辑回归（LR）

1.4. 算法步骤

SVM算法可以分为以下几个步骤：

1. 数据预处理：将数据集划分为训练集和测试集，并进行特征缩放（对数据进行标准化）。

2. 构建模型：选择合适的核函数和惩罚系数，构建SVM模型。

3. 训练模型：使用训练集对模型进行训练，通过最大化间隔来找到最优的超平面。

4. 预测：使用训练好的模型对测试集进行预测。

1.5. 分类和回归的选择

通常情况下，当标签值是离散型变量时，我们将问题视为分类问题，而当标签值是连续性变量时，我们将问题视为回归问题。

在支持向量机（SVM）算法中，SVC用于分类，SVR用来做回归

1. 在分类问题中，我们的目标是将输入数据分为不同的离散类别。常见的分类算法包括逻辑回归、决策树、随机森林和支持向量机等。

2. 在回归问题中，我们的目标是预测连续性变量的值。回归问题涉及到对输入数据进行建模，以预测一个或多个连续的输出变量。常见的回归算法包括线性回归、决策树回归、支持向量回归和神经网络等。

二、代码实现（SVM）

1. SVR（回归）

使用波士顿房价数据集，其标签值是一个连续型变量，故用SVR来做回归问题

波士顿房价数据集介绍：

#加载波士顿房价数据集
from sklearn.datasets import load_boston
boston = load_boston()
x = boston.data
y = boston.target

#数据的划分
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x,y,random_state=42)

#标准化
from sklearn import preprocessing
scaler = preprocessing.StandardScaler().fit(x_train)
#保证train数据与test数据是在统一的距离标准下进行的标准化
x_train = scaler.transform(x_train)
x_test = scaler.transform(x_test)

#SVM构建
from sklearn.svm import SVR
#使用多项式核函数
model = SVR(kernel= "poly",degree= 3 ,C=5)
model.fit(x_train,y_train)
#检查得分
print(model.score(x_test,y_test))
# print(model.predict(x_test))

#使用高斯核函数
model2 = SVR(kernel="rbf",gamma=0.01,C=5)
# print(model2)
model2.fit(x_train,y_train)
print(model2.score(x_test,y_test))

#使用sigmoid核函数
model = SVR(kernel= "sigmoid",gamma=0.01 ,C=5)
model.fit(x_train,y_train)
#检查得分
print(model.score(x_test,y_test))
# print(model.predict(x_test))



#使用网格搜索
import numpy as np
from sklearn.model_selection import GridSearchCV
params = {
    "kernel": ["rbf","sigmoid","poly","linear"],
    "C": np.arange(1,6),
    "gamma": np.arange(0,0.5,0.001),
    "degree":np.arange(1,5)
}
grid_searchcv = GridSearchCV(SVR(),param_grid= params,cv= 5)
grid_searchcv.fit(x_train,y_train)
print(grid_searchcv.best_params_)
print(grid_searchcv.best_score_)
#print(grid_searchcv.cv_results_)
print(grid_searchcv.best_index_)
print(grid_searchcv.best_estimator_)
best_clf = grid_searchcv.best_estimator_
best_clf.fit(x_train,y_train)
print(best_clf.score(x_test,y_test))

#结果
{'C': 5, 'degree': 1, 'gamma': 0.058, 'kernel': 'rbf'}
0.7854834638941114
24232
SVR(C=5, degree=1, gamma=0.058)
0.7698971297133513

2. 回归结果可视化

from sklearn.svm import SVR
best_clf = SVR(kernel= "rbf",degree= 1 ,C=5,gamma=0.058)
best_clf.fit(x_train,y_train)

import matplotlib.pyplot as plt
# 使用最佳模型进行预测
y_pred = best_clf.predict(x_test)

# 绘制预测值与真实值之间的散点图
plt.scatter(y_test, y_pred)
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--', lw=2)
plt.xlabel('True Values')
plt.ylabel('Predicted Values')
plt.title('SVM Regression - True Values vs Predicted Values')
plt.show()

在图中，如果点分布在对角线附近，则表示预测值与真实值较为接近，说明模型的回归效果较好。反之则不好

3. SVC（分类）

使用鸢尾花数据集，因为其标签值为离散型变量，故用SVC来做分类问题

#加载iris数据集
from sklearn.datasets import load_iris
iris = load_iris()
x = iris.data
y = iris.target

#数据的划分
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x,y,random_state=42)

#标准化
from sklearn import preprocessing
scaler = preprocessing.StandardScaler().fit(x_train)
#保证train数据与test数据是在统一的距离标准下进行的标准化
x_train = scaler.transform(x_train)
x_test = scaler.transform(x_test)

#使用网格搜索
from sklearn.svm import SVC
import numpy as np
from sklearn.model_selection import GridSearchCV
params = {
    "kernel": ["rbf","sigmoid","poly","linear"],
    "C": np.arange(1,6),
    "gamma": np.arange(0,0.5,0.001),
    "degree":np.arange(1,4)
}
grid_searchcv = GridSearchCV(SVC(),param_grid= params,cv= 5)
grid_searchcv.fit(x_train,y_train)
print(grid_searchcv.best_params_)
print(grid_searchcv.best_score_)
print(grid_searchcv.best_index_)
print(grid_searchcv.best_estimator_)
best_clf = grid_searchcv.best_estimator_
best_clf.fit(x_train,y_train)
print(best_clf.score(x_test,y_test))
print(best_clf.predict(x_test))

#结果
{'C': 1, 'degree': 1, 'gamma': 0.133, 'kernel': 'poly'}
0.9640316205533598
534
SVC(C=1, degree=1, gamma=0.133, kernel='poly')
1.0
[1 0 2 1 1 0 1 2 1 1 2 0 0 0 0 1 2 1 1 2 0 2 0 2 2 2 2 2 0 0 0 0 1 0 0 2 1
 0]

3. 分类结果可视化

因为鸢尾花数据集有四个特征，所以为了方便可视化，要将数据集进行降维

# 使用PCA进行降维
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
x_pca = pca.fit_transform(x)
#数据的划分
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x_pca,y,random_state=42)

#标准化
from sklearn import preprocessing
scaler = preprocessing.StandardScaler().fit(x_train)
#保证train数据与test数据是在统一的距离标准下进行的标准化
x_train = scaler.transform(x_train)
x_test = scaler.transform(x_test)

import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
best_clf = SVC(degree= 1,C= 1,gamma= 0.133,kernel="poly")
best_clf.fit(x_train,y_train)
# 使用最佳模型进行预测
y_pred = best_clf.predict(x_test)

# 绘制散点图
sc = plt.scatter(x_test[:, 0], x_test[:, 1], c=y_pred)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('SVM Classification - Predicted Classes')
handles, labels = sc.legend_elements()
plt.legend(handles, labels)
plt.show()


# 绘制决策边界图
h = 0.02  # 步长
x_min, x_max = x_test[:, 0].min() - 1, x_test[:, 0].max() + 1
y_min, y_max = x_test[:, 1].min() - 1, x_test[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = best_clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.8)
plt.scatter(x_test[:, 0], x_test[:, 1], c=y_pred)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('SVM Classification - Decision Boundary')
plt.show()

4. 非线性分类

from sklearn.datasets import make_moons
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
plt.style.use("ggplot")
# 生成非线性分类数据
X, y = make_moons(n_samples=200, noise=0.05,random_state=41)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建SVM模型并指定核函数
svm = SVC(kernel='rbf', random_state=42)
svm.fit(X_train, y_train)
y_pred = svm.predict(X_test)

# 计算分类准确率
accuracy = accuracy_score(y_test, y_pred)
# print( accuracy)

# 绘制分类结果
sc= plt.scatter(X_test[:, 0], X_test[:, 1], c=y_pred, cmap='viridis')
plt.xlabel('X1')
plt.ylabel('X2')
plt.title('Nonlinear Classification')
handles,labels =sc.legend_elements()
plt.legend(handles,labels)
plt.show()

绘制决策边界图

# 绘制决策边界图
def plot_juecebianjie(model, X, y):
    # 定义绘图边界
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    h = 0.02  # 步长

    # 生成网格点坐标矩阵
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))

    # 使用模型进行预测
    Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    # 绘制等高线图
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral, alpha=0.6)

    # 绘制数据点
    sc= plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Spectral)
    plt.xlabel('X1')
    plt.ylabel('X2')
    plt.title('Decision Boundary')
    handles,labels = sc.legend_elements()
    plt.legend(handles,labels)
    plt.show()

# 调用函数
plot_juecebianjie(svm, X_test, y_pred)

---

总结

本文在SVM算法原理介绍中：从开始的SVM介绍，到Kernel的介绍，再到算法和核函数的选择，之后就是算法的步骤，以及分类和回归的选择；在代码实现中：亦是分别对SVM中的回归（SVR)和分类（SVC）用代码实现，并可视化结果。

关关雎鸠，在河之洲

–2023-9-4 筑基篇