球谐函数实现环境光照漫反射实践
该文章以及代码主要来自
图形学论文解析与复现:【论文复现】An Efficient Representation for Irradiance Environment Maps
作者:Monica的小甜甜
与原文的不同:
- 对一些有问题的地方进行了修改
- 添加了注释
- 对有疑问的地方添加了疑问点
- 引入了其他一些Blog填充了原文中忽略的信息
1、预计算球面谐波函数系数
首先根据上一篇【球谐函数在环境光照中的使用原理】得到的最终公式:
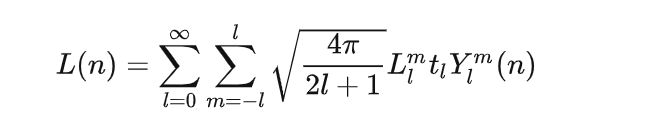
我们需要预计算 L l m L_l^m Llm的值。计算公式为:

Ω \Omega Ω为球面积分,这里对应对天空盒逐像素积分。
积分代码为:
void Harmonics::Evaluate()//求值
{
m_Coefs = vector<glm::vec3>(m_Degree, glm::vec3());
//6张图
for (int k = 0; k < 6; k++)
{
cv::Mat img = m_Images[k];
int w = m_Images[k].cols;
int h = m_Images[k].rows;
//逐像素
for (int j = 0; j < w; j++)
{
for (int i = 0; i < h; i++)
{
// 像素点位置
float px = (float)i + 0.5;
float py = (float)j + 0.5;
// 像素点UV 【-1,1】:以摄像机正对位置的(0,0)
float u = 2.0 * (px / (float)w) - 1.0;
float v = 2.0 * (py / (float)h) - 1.0;
// 像素间UV的一半的偏移量
float d_x = 1.0 / (float)w;
// (x0,y0)像素左下角 (x1,y1)像素右上角
float x0 = u - d_x;
float y0 = v - d_x;
float x1 = u + d_x;
float y1 = v + d_x;
// 计算Cubemap的一个像素对应的立体角的大小
float d_a = surfaceArea(x0, y0) - surfaceArea(x0, y1) - surfaceArea(x1, y0) + surfaceArea(x1, y1);
// 纹理像素点 转化为 世界坐标点
u = (float)j / (img.cols - 1);
v = 1.0f - (float)i / (img.rows - 1);
glm::vec3 p = CubeUV2XYZ({ k, u, v });
// 获取当前像素颜色
auto c = img.at<cv::Vec3f>(i, j);
glm::vec3 color = {c[2], c[1], c[0]};
// 得到基函数计算结果列表
vector<float> Y = Basis(p);
// 计算系数
for (int i = 0; i < m_Degree; i++)
{
m_Coefs[i] = m_Coefs[i] + Y[i] * color * d_a;
}
}
}
}
}
其中 计算Cubemap的一个像素对应的立体角的大小原理可参照
Solid Angle of A Cubemap Texel - 计算Cubemap的一个像素对应的立体角的大小
我们将得到的积分结果保存在一个文件中【SHCoefficients.txt】,用于之后读取。
2、预计算BRDF的LUT图
LUT(Look up Table)图,预计算了任意一个天空盒下,已知法线和视口的夹角以及材质粗糙度,查找得到Frenel项。
然而这个LUT图和IBL中的LUT有一些不同。
因为IBL中的LUT加入了 n ⋅ w n\cdot w n⋅w 光照衰减项。
而在球谐函数中, n ⋅ w n\cdot w n⋅w 作为 t l 参与运算 t_l参与运算 tl参与运算,因此在球谐函数的IBL中删除了 n ⋅ w n\cdot w n⋅w。
main函数计算
for(int i = 0; i < N; i++){
for (int j = 0; j < N; j++)
{
float NoV = (i + 0.5f) * (1.0f / N);
float roughness = (j + 0.5f) * (1.0f / N);
glm::vec2 eval = IntegrateBRDF(NoV, roughness);
tex.store<glm::vec2>({ i, N - j - 1 }, 0, eval);
}
}
其他被调用函数
const float PI = 3.14159265358979323846264338327950288;
float RadicalInverse_VdC(unsigned int bits)
{
bits = (bits << 16u) | (bits >> 16u);
bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u);
bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u);
bits = ((bits & 0x0F0F0F0Fu) << 4u) | ((bits & 0xF0F0F0F0u) >> 4u);
bits = ((bits & 0x00FF00FFu) << 8u) | ((bits & 0xFF00FF00u) >> 8u);
return float(bits) * 2.3283064365386963e-10;
}
glm::vec2 Hammersley(unsigned int i, unsigned int N)
{
return glm::vec2(float(i) / float(N), RadicalInverse_VdC(i));
}
glm::vec3 ImportanceSampleGGX(glm::vec2 Xi, float roughness, glm::vec3 N)
{
float a = roughness * roughness;
float phi = 2.0 * PI * Xi.x;
float cosTheta = sqrt((1.0 - Xi.y) / (1.0 + (a*a - 1.0) * Xi.y));
float sinTheta = sqrt(1.0 - cosTheta * cosTheta);
// from spherical coordinates to cartesian coordinates
glm::vec3 H;
H.x = cos(phi) * sinTheta;
H.y = sin(phi) * sinTheta;
H.z = cosTheta;
// from tangent-space vector to world-space sample vector
glm::vec3 up = abs(N.z) < 0.999 ? glm::vec3(0.0, 0.0, 1.0) : glm::vec3(1.0, 0.0, 0.0);
glm::vec3 tangent = normalize(cross(up, N));
glm::vec3 bitangent = cross(N, tangent);
glm::vec3 sampleVec = tangent * H.x + bitangent * H.y + N * H.z;
return normalize(sampleVec);
}
float GeometrySchlickGGX(float NdotV, float roughness)
{
float a = roughness;
float k = (a * a) / 2.0;
float nom = NdotV;
float denom = NdotV * (1.0 - k) + k;
return nom / denom;
}
float GeometrySmith(float roughness, float NoV, float NoL)
{
float ggx2 = GeometrySchlickGGX(NoV, roughness);
float ggx1 = GeometrySchlickGGX(NoL, roughness);
return ggx1 * ggx2;
}
glm::vec2 IntegrateBRDF(float NdotV, float roughness, unsigned int samples = 1024)
{
glm::vec3 V;
V.x = sqrt(1.0 - NdotV * NdotV);
V.y = 0.0;
V.z = NdotV;
float A = 0.0;
float B = 0.0;
glm::vec3 N = glm::vec3(0.0, 0.0, 1.0);
for (unsigned int i = 0u; i < samples; ++i)
{
glm::vec2 Xi = Hammersley(i, samples);
glm::vec3 H = ImportanceSampleGGX(Xi, roughness, N);
glm::vec3 L = normalize(2.0f * dot(V, H) * H - V);
float NoL = glm::max(L.z, 0.0f);
float NoH = glm::max(H.z, 0.0f);
float VoH = glm::max(dot(V, H), 0.0f);
float NoV = glm::max(dot(N, V), 0.0f);
if (NoL > 0.0)
{
float G = GeometrySmith(roughness, NoV, NoL);
float G_Vis = (G * VoH) / (NoH * NoV) / NoL;
float Fc = pow(1.0 - VoH, 5.0);
A += (1.0 - Fc) * G_Vis;
B += Fc * G_Vis;
}
}
return glm::vec2(A / float(samples), B / float(samples));
}
3、将计算数据传入Shader
- 传入BRDFLUT纹理
- 传入球谐函数系数列表
void CShadingPass::initV()
{
auto m_LUTTexture = std::make_shared<ElayGraphics::STexture>();
loadTextureFromFile("../Textures/BRDFLUT/BRDFLut.dds", m_LUTTexture);
getCoefs();
ElayGraphics::Camera::setMainCameraFarPlane(100);
ElayGraphics::Camera::setMainCameraPos({ -1.57278, 0.244948, 0.367194 });
ElayGraphics::Camera::setMainCameraFront({ 0.967832, -0.112856, -0.224865 });
ElayGraphics::Camera::setMainCameraMoveSpeed(0.5);
m_pShader = std::make_shared<CShader>("Sponza_VS.glsl", "Sponza_FS.glsl");
m_pSponza = std::dynamic_pointer_cast<CSponza>(ElayGraphics::ResourceManager::getGameObjectByName("Sponza"));
m_pShader->activeShader();
m_pShader->setTextureUniformValue("u_BRDFLut", m_LUTTexture);
m_pShader->setMat4UniformValue("u_ModelMatrix", glm::value_ptr(m_pSponza->getModelMatrix()));
for (int i = 0; i < m_Coefs.size(); i++)
{
m_pShader->setFloatUniformValue("u_Coef[" + std::to_string(i) + "]", m_Coefs[i].x, m_Coefs[i].y, m_Coefs[i].z);
}
m_pSponza->initModel(*m_pShader);
}
4、 Draw
#version 430 core
in vec3 v2f_FragPosInViewSpace;
in vec2 v2f_TexCoords;
in vec3 v2f_ViewSpaceNormal;
in vec3 v2f_WorldSpaceNormal;
layout (location = 0) out vec4 Albedo_;
const float PI = 3.1415926535897932384626433832795;
uniform vec3 u_Coef[16];
uniform vec3 u_DiffuseColor;
uniform sampler2D u_BRDFLut;
vec3 FresnelSchlickRoughness(float cosTheta, vec3 F0, float roughness)
{
return F0 + (max(vec3(1.0 - roughness), F0) - F0) * pow(max(1.0 - cosTheta, 0.0), 5.0);
}
void main()
{
if((abs(v2f_ViewSpaceNormal.x) < 0.0001f) && (abs(v2f_ViewSpaceNormal.y) < 0.0001f) && (abs(v2f_ViewSpaceNormal.z) < 0.0001f))
{
Albedo_ = vec4(0, 0, 0, 1);
return;
}
float Basis[9];
float x = v2f_WorldSpaceNormal.x;
float y = v2f_WorldSpaceNormal.y;
float z = v2f_WorldSpaceNormal.z;
float x2 = x * x;
float y2 = y * y;
float z2 = z * z;
//这里所有系数应该为乘PI------------------个人认为
Basis[0] = 1.f / 2.f * sqrt(1.f / PI);
Basis[1] = 2.0 / 3.0 * sqrt(3.f / 4.f * PI) * z;
Basis[2] = 2.0 / 3.0 * sqrt(3.f / 4.f * PI) * y;
Basis[3] = 2.0 / 3.0 * sqrt(3.f / 4.f * PI) * x;
Basis[4] = 1.0 / 4.0 * 1.f / 2.f * sqrt(15.f * PI) * x * z;
Basis[5] = 1.0 / 4.0 * 1.f / 2.f * sqrt(15.f * PI) * z * y;
Basis[6] = 1.0 / 4.0 * 1.f / 4.f * sqrt(5.f * PI) * (-x2 - z2 + 2 * y2);
Basis[7] = 1.0 / 4.0 * 1.f / 2.f * sqrt(15.f * PI) * y * x;
Basis[8] = 1.0 / 4.0 * 1.f / 4.f * sqrt(15.f * PI) * (x2 - z2);
vec3 Diffuse = vec3(0,0,0);
vec3 F0 = vec3(0.2,0.2,0.2);
float Roughness = 0.5;
vec3 N = normalize(vec4(v2f_ViewSpaceNormal,1.0f)).xyz;//viewMatrix *
vec3 V = -normalize(v2f_FragPosInViewSpace);
//vec3 R = reflect(-V, N);
F0 = FresnelSchlickRoughness(max(dot(N, V), 0.0), F0, Roughness);
vec2 EnvBRDF = texture(u_BRDFLut, vec2(max(dot(N, V), 0.0), Roughness)).rg;
vec3 LUT = (F0 * EnvBRDF.x + EnvBRDF.y);
for (int i = 0; i < 9; i++)
Diffuse += u_Coef[i] * Basis[i] * (1-LUT);
Albedo_ = vec4(Diffuse);
}


