JDK源码剖析之PriorityQueue优先级队列

写在前面

版本信息：
JDK1.8

PriorityQueue介绍

在数据结构中，队列分为FIFO、LIFO 两种模型，分别为先进先出，后进后出、先进后出，后进先出（栈） 而一切数据结构都是基于数组或者是链表实现。

在Java中，定义了Queue接口，接口中定义了CRUD的基本方法。分别add、offer、remove、poll等等，而PriorityQueue 实现此接口实现了基本的CRUD的同时拥有了自己的特性，从名字来看也能知道是优先级队列 ： 保持队列头部节点是整条队列中永远是最小或者最大的节点，其实现原理就是一个小顶堆或者大顶堆。上文提及到一切数据结构都是基于数组或者是链表实现，而这里使用了数组实现。

public class PriorityQueue extends AbstractQueue
    implements java.io.Serializable {
    transient Object[] queue;    // 由数组实现
}

public abstract class AbstractQueue
    extends AbstractCollection
    implements Queue {}

小顶堆和大顶堆介绍

从上文描述了PriorityQueue的底层实现是小顶堆或者大顶堆，那么在看源码之前，我们需要先明白小顶堆和大顶堆如何实现～

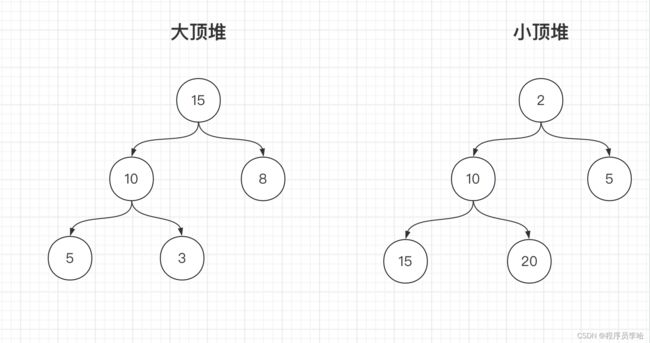
小顶堆：一颗完全二叉树，其中任意父节点都要小于左右子节点，所以树的根节点是整棵树的最小节点

大顶堆：一颗完全二叉树，其中任意父节点都要大于左右子节点，所以树的根节点是整棵树的最大节点

Comparable和Comparator区别

在看PriorityQueue源码之前还需要分析Comparable和Comparator区别。

Comparable：类需要实现此接口，重写compareTo方法，在compareTo方法中定义比较逻辑，使用时把类强转成Comparable调用compareTo方法，把比较对象传入。所以侵入性比较强，与业务代码强耦合。

Comparator：这个就是一个比较器，只需要把A比较对象和B比较对象都传入即可，不需要于业务代码强耦合

PriorityQueue添加元素源码分析

下文直接把PriorityQueue叫成小顶堆

我们直接从offer方法入手～

public boolean offer(E e) {
    if (e == null)
        throw new NullPointerException();
    modCount++;        // 用于检测是否并发
    // 因为size从0开始，所以size的值就是数组的索引值。
    int i = size;

    // 是否需要扩容
    if (i >= queue.length)
        grow(i + 1);  

    // 为下次索引+1
    size = i + 1;

    // 如果是第一个，那么就直接占用数组第一个元素即可，
    // 因为不管是小顶堆还是大堆堆第一个都直接插入。
    if (i == 0)
        queue[0] = e;
    else
        // 非第一个节点，此时就需要调整
        siftUp(i, e);
    return true;
}

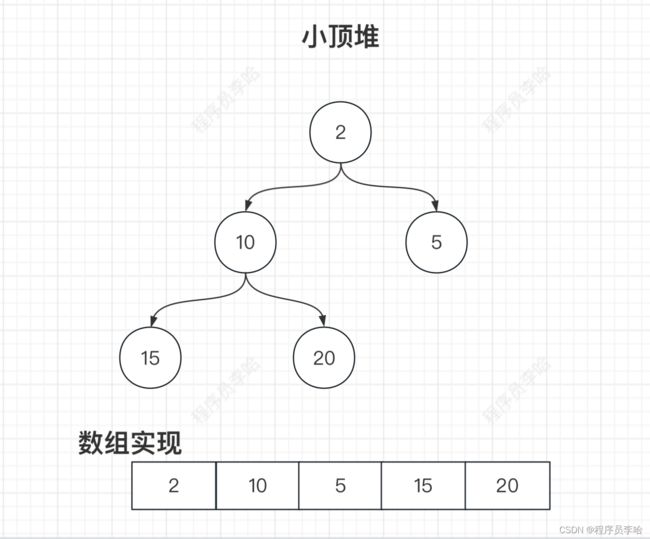
这里的逻辑比较简单，因为这里使用数组实现的小顶堆（也即使用数组实现完全二叉树），而小顶堆的第一个节点是最小的，所以当0索引直接插入即可，非0索引就需要调整小顶堆。这里应该有很多读者是第一次见数组实现二叉树，所以这里把上文的二叉树进行扩展，把数组部分画上去。

在看 siftUp调整方法前，我们看一下grow扩容方法， 因为里面有一个思路大家可以学习～

private void grow(int minCapacity) {
    int oldCapacity = queue.length;
    
    // 容量小于64时，扩容为 oldCapacity + oldCapacity +2 
    // 容量大于64，扩容为 oldCapacity + oldCapacity/2
    // 等同于，在容量小的时候，每次扩容大一些，当达到64这个阈值后，扩容小一些，要不然空间会太浪费了～
    int newCapacity = oldCapacity + ((oldCapacity < 64) ?
       (oldCapacity + 2) :
       (oldCapacity >> 1));

    if (newCapacity - MAX_ARRAY_SIZE > 0)
        newCapacity = hugeCapacity(minCapacity);
    // 数组拷贝迁移。
    queue = Arrays.copyOf(queue, newCapacity);      
}

在每次扩容的时候，会去判断，当前容量是否大于64，如果小于64就直接 原大小 * 2 + 2 扩容，如果大于64以后直接 原大小 + 原大小/2 扩容。目的是为了在容量小的时候扩容大一些，减少扩容次数。在容量达到64阈值后，扩容小一些，减少内存浪费。

下面开始讲解siftUp调整方法

private void siftUp(int k, E x) {
    // 用户是否传入comparator比较器
    if (comparator != null)
        siftUpUsingComparator(k, x);
    else
        // 没传入就使用Comparable
        // 此时类需要实现Comparable接口
        siftUpComparable(k, x);
}

这里讲解siftUpComparable方法，本质上两个方法没任何区别～

private void siftUpComparable(int k, E x) {
    Comparable key = (Comparable) x;
    while (k > 0) {
        // 拿到父节点
        // 因为是使用数组实现的一颗完全二叉树，所以直接-1 右移即可拿到当前插入节点的父节点
        int parent = (k - 1) >>> 1;

        Object e = queue[parent];
        // 与父节点做比较。
        if (key.compareTo((E) e) >= 0)
            // 达到用户的预期比较就直接break，要不然继续往父节点的父节点继续做比较，直到根节点
            break;
        // 没达到预期，所以把父节点插入到本次插入的节点的位置。
        queue[k] = e;
        // 拿到父节点的索引，继续往父节点的父节点做比较。
        k = parent;
    }
    // 插入
    queue[k] = key;
}

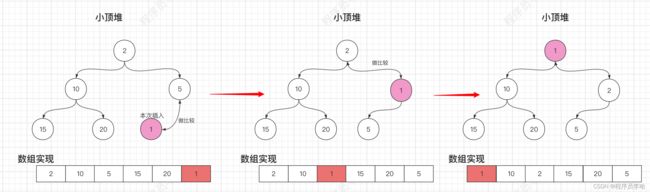
这里光看注释，肯定是看不明白的，所以以画图+注释来理解吧～

PriorityQueue获取元素源码分析

直接从poll方法入手～

public E poll() {
    if (size == 0)
        return null;
    // 拿到最后一个节点的索引值。
    int s = --size;
    modCount++;
    // 因为第一个是小顶堆或者大顶堆要的数据。
    E result = (E) queue[0];
    // 拿到最后一节点
    E x = (E) queue[s];
    queue[s] = null;   // help gc
    if (s != 0)
        // 调整
        siftDown(0, x);
    return result;
}

因为小顶堆或者大顶堆都是拿第一个元素，所以这里拿出第一个元素。但是每次拿完就需要调整小顶堆（调整完全二叉树），所以看到siftDown方法。

private void siftDown(int k, E x) {
    if (comparator != null)
        siftDownUsingComparator(k, x);
    else
        siftDownComparable(k, x);
}

本质上这两个方法没任何区别，所以继续看到siftDownComparable方法

// k为0
// x是最后一个节点。
private void siftDownComparable(int k, E x) {
    Comparable key = (Comparable)x;

    // 循环的次数
    // 是通过数组的大小 右移一位就可以知道树高了。
    int half = size >>> 1;        
    while (k < half) {
        // 往下层找。
        int child = (k << 1) + 1; 
        Object c = queue[child];    // 左子节点
        int right = child + 1;      // 右子节点

        // 左右子节点比较，那个满足规范就作为父节点
        if (right < size &&
            ((Comparable) c).compareTo((E) queue[right]) > 0)
            // 右节点满足于左节点
            c = queue[child = right];
        // 与最后一个节点比较后，达到预期直接退出
        if (key.compareTo((E) c) <= 0)
            break;
        // 替换
        queue[k] = c;
        // 下次循环的父节点
        k = child;
    }
    queue[k] = key;
}

因为每次poll取走的是第一个元素，所以需要调整整个小顶堆，而第一个元素是小顶堆的根节点，所以需要调整小顶堆找到一个符合的元素作为根节点。从根节点的左右子节点开始比较，左右子节点比较出预期的节点就作为新的根节点。预期的节点作为下次比较的父节点，通过父节点再找到他的左右子节点做比较，周而复始，直到最后一个节点。

这里光看注释，肯定是看不明白的，所以以画图+注释来理解吧～