密码学编程

Python 密码学编程

凯撒密码

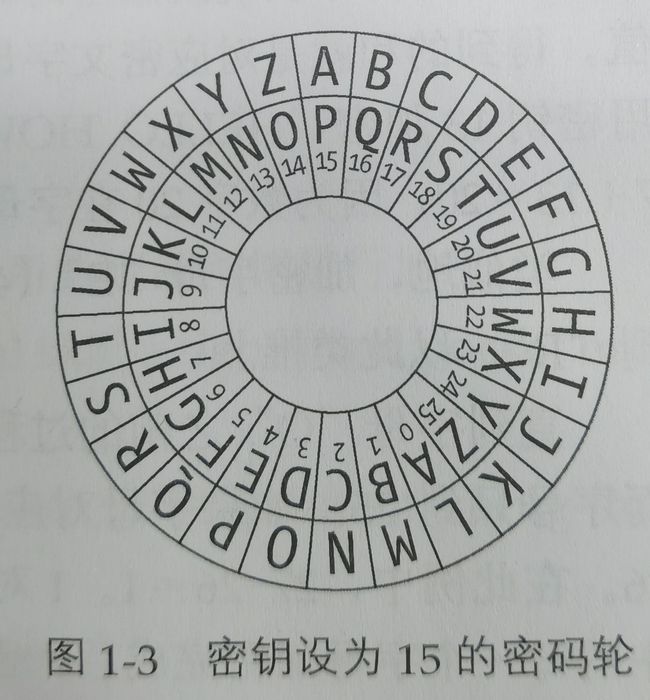
凯撒密码通过替换字母完成加密，每个字母由字母表中其后特定数位的字母代替。例如，Julius Caesar将字母向后移动3个字母的位置，然后用得到的新字母表中的字母替换原消息中的每个字母。

我们可以通过下图的密码轮进行理解。其中最外圈为初始的字符，而相邻的内圈层对应的字符就是密匙设置为15的凯撒编码(这个15可以理解为本来A是与$A_0$对应的现在被拨到与$P_{15}$对应，这个过程中所有的字母的对应关系都发生了相同的偏移)。

实现的过程其实就是与这个密码轮类似的。首先给定一个字符集(其中不能有重复字符)、一个密匙。加密时先找到字符在字符集中的位置，若找到则按照给定的密匙进行偏移映射得到对应的密码，若找不到就不加密原字符即为密码。

置换密码

用置换密码进行的加密算法的步骤如下：

1. 计算消息和密匙中字符的个数
2. 绘制一行个数等于密匙值的空框(例如，密匙为8，绘制8个框)
3. 从左到右开始对框进行填充，每个框内放一个字符
4. 当框已经填满但还有剩余字符是，再添加一个空框
5. 到最后一个字符时，为最后一行未使用的框涂上阴影
6. 从左上方开始，每列依次向下写出字符。当达到一列的底部时，移到右侧一列，并跳过阴影框。这样写出的结果就是密文。

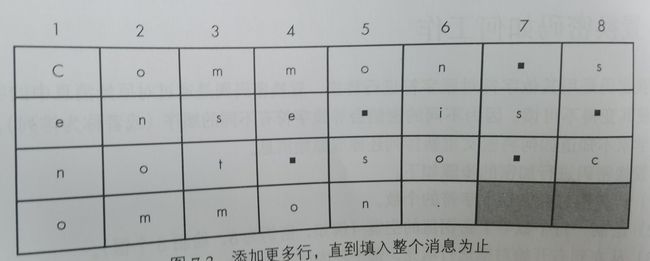
上述的过程很复杂，但是其实过程很简单。对其翻译一下就是将原始的字符按顺序(从左到右，或者说行优先)填充到固定宽度的表格中，然后使用与填充顺序不同（比如从上到下 或者说是列优先）的方式读取出来的字符串就是对应的密码。

例子

我们用置换密码的方式对Common sense is not so common.进行加密，得到的密文为Cenoonommstmme oo snnio. s s c。下图为加密过程中得到的填表， 可以结合前面的说明进行理解。

仿射密码

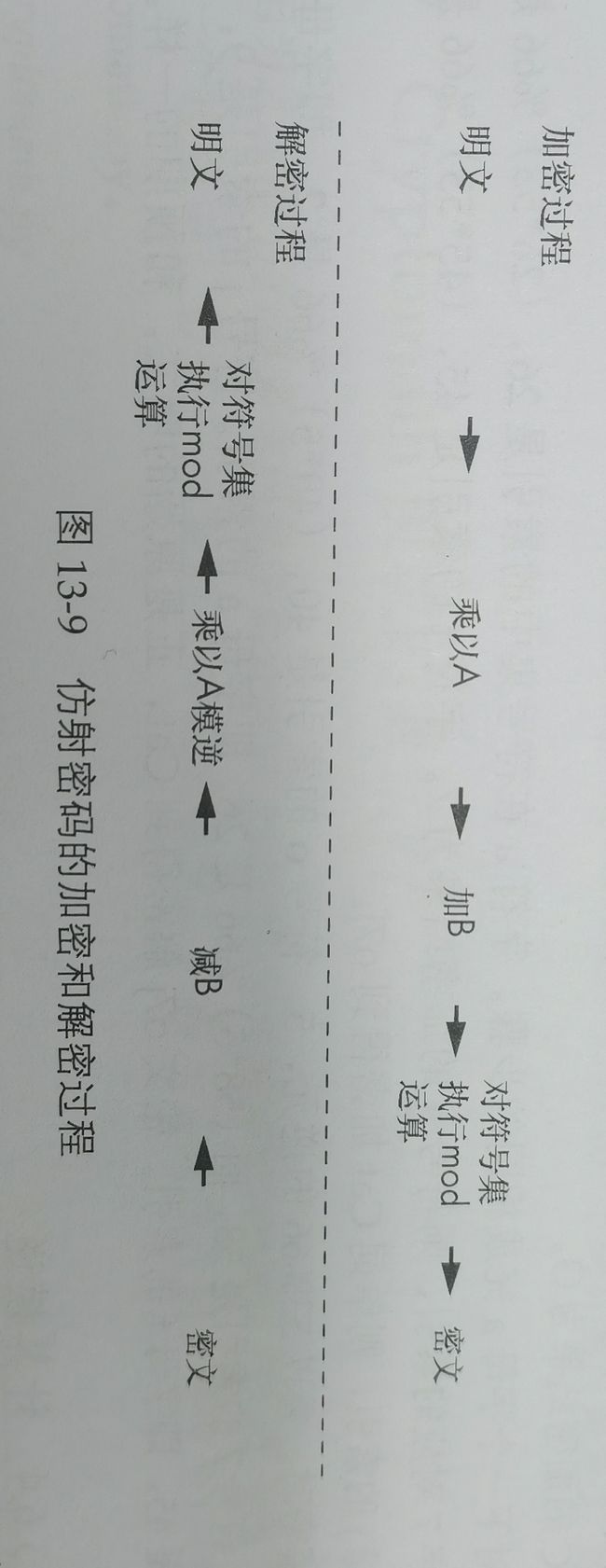
仿射密码的加密和解密的过程

破解分析

其中包含两个密匙分别为：乘法的密匙记为KeyA、凯撒的移位密匙记为KeyB.记字符集为T.

上述两种密匙的个数分析：

• 乘法密匙 KeyA需要与 len(T)互为质数，因此KeyA的个数要小于$2//len(T)$
• 凯撒密匙 KeyB的移位密匙，我们不难理解当KeyB与KeyB + len(T)的两种效果是相同的。因此KeyB共有len(T)种可能。

同时我们可以通过上面的流程图看出两种方法的，是按照一定的先后关系的。可以理解为排列，所以若要暴力破解仿射密匙需要尝试$(2//len(T))\ast len(T)<=len(T{)}^2$ .

代换密码

我们可以总结前面三种加密方式，其实加密的过程都是对原始字符做了一个在给定字符集中的映射。

代换密码其实就是用了最直接的方式给出这种映射关系，即给出对应的映射关系表。如下图就是这种映射关系的表。

维吉尼亚密码

与凯撒密码不同，维吉尼亚密码时一种多密匙。它使用了不止一种代换方式，又被称为多表代换密码，这也使得用于破解简单代换密码的频率无法独自攻破维吉尼亚密码。

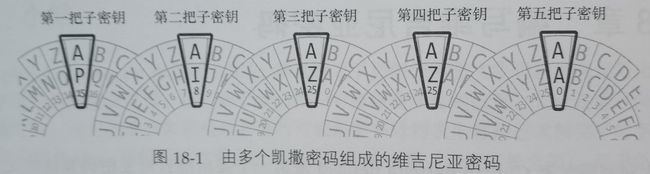
维吉尼亚密码的密匙是一系列字母的组合，比如一个英文单词，这个字母的组合会被分成多个单字母的子密匙用以加密明文字母。如果将维吉尼亚密码的密匙设置为单词PIZZA,第一把子密匙就是P，第二把子密匙时I……以此类推。遇到明文的第六个字母的时候，重新回到第一把子密匙。

如下图所示，使用维吉尼亚密码的方法和使用多个凯撒密码的方法是一样的。不同的是，维吉尼亚密码并不用单独的一把密匙加密明文的所有字母，而是对明文的每一个字母使用不同的密匙。

维吉尼亚密码其实就是采用了一组凯撒密码的方式对数据进行加密。假设我们只对大小写字母进行加密那么就是有26个字符可加密，记密匙长度为N则暴力破解对应的可能密匙数为$26^N$.不难设想这种指数型的增长速度是多快。也因此维吉尼亚密码加密时密匙越长越难被破解。

维吉尼亚密码的破解-运用Kasiski检测确定密匙长度

找到重复序列

因为同一个字母用同一把密匙加密的结果是相同的。因此我们可以在密文中找到重复的序列，并找到不同的重复序列中频率最高的间隔数。这些重复序列的间隔数被认为较有可能是为吉尼亚密码的正确长度。

使用频率分析法逐个破解子密匙

为了进一步检验密匙长度的正确性。例如我们检验密匙长度为4是否正确。记密文为Str,我们将Str看做是每4个字母组合得到的字符串。将每组中的第i个字符进行拼接获得新的子串（这些字串可以理解为维吉尼亚密码退化为凯撒密码加密得到的子串）。再对得到的4子串进行频率分析，因为若密匙长度正确那么每个子串中的字符都由同一个密匙加密得到在大量数据的情况下应保持英文字符在自然情况下的分布。

前面解密的两个步骤，其实是对最有可能的密匙进行猜测。也就是提高了先猜到密匙的可能性。

一次一密

一次一密是维吉尼亚密码的一种，当密匙满足以下标准时，密码将变得不可破解。

• 它和加密的消息一样长
• 它是由真正随机的符号组成
• 它一旦使用过以此，就不会再用于其他任何消息

遵循这3个规则，可以使加密的消息不被任何密码分析员攻破。即使有无限的计算能力，密码也始终安全。

在有了前面对维吉尼亚密码的破解过程我们可以理解一次一密不可破解的原因。普通维吉尼亚密码容易受到攻击的原因是，通过猜测最有可能的密匙长度和字母频率分析可以来解码。但是在一次一密的加密过程中每个明文字母的密匙都不同，意味着每个明文字母可以以相同的频率被加密到任意密文字母

公钥密码体制

设想一下世界另一遍的某个人想和你交流，但是需要互相发送加密信息。按照前面提到的加密方法，双发必须就使用什么密匙达成共识。但密钥交流的过程中也可能被拦截。

公钥密码体制通过使用(一个用于加密，一个用于解密)解决了这种加密问题，它是不对称密码的例子。使用相同的密钥进行加密和解密的密码，属于对称密码。

在公钥密码体系中：使用加密密钥（公钥）加密的消息只能使用解密密钥（私钥）来解密。因此，即使有人获得加密密钥，他们也不能读取原始消息，因为加密密钥并不能解密消息。

认证问题

前面介绍的公钥加密的方法看起来很完美，不对称性让除信息发送者外没人能解密收到的回复。再仔细思考一下，加粗的部分"信息发送者"。

虽然公钥密码以及前面介绍的其他密码都可以保证机密性，但它们并不总是提供身份验证。

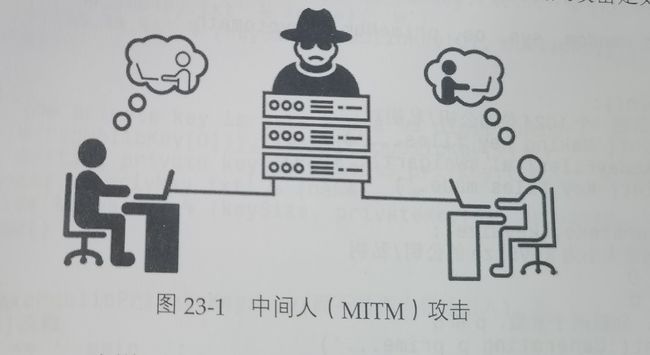
通常，在对称密码这不是个问题，因为面对面交换密钥时可以看到对方是谁。但是，在使用公钥时，在开始向对方发送消息的时候不需要看到他就可以获取他的公钥。利用这个漏洞，进行中间人或称为中间机器(MITM)的攻击方式（利用不进行身份验证的漏洞）。

有一个领域称为公钥基础设施（PKI）,供公钥的发送双方来验证对方的身份，这在一定程度上保证了安全。

中间人攻击：

比如A与B正在交流，中间人通过对消息进行拦截。B对A交流时拦截B的消息并将其中的公钥替换成自己的公钥，相同的在A对B交流的过程中将A发送的消息中的公钥替换成自己的公钥。这样中间人就可以很方便地知道其中所有的交流细节，而A和B却浑然不知。

公钥密码算法

下面描述的公钥密码算法是RSA

公钥密码算法需要在数字组合成的分组上进行操作的原因是，如果只对一个字符使用公钥密码进行加密，明文中相同的字母经过相同的加密得到了相同的密文。这样的画公钥密码算法就和代换密码本质上没有什么区别了。

分组的创建

在密码学中，一个分组是一个由固定位数的字符串组合而生成的大整数。分组的长度的上限取决于字符集的长度和密钥长度。

分组确定的过程需满足$2^{keysize}>字符{集}^{blocksize}$（key size 是密钥长度， block size 是分组长度）。如果分组长度太大，公钥密码算法所依赖的数学原理将不起作用！

字符串转化为分组

首先我们需要准备一个字符集表示为SYMBOLS，待加密的分组字符串记为msg.可以按照下式计算合成的大整数：
$$S=\prod _{i=0}^{len(msg)-1}SYMBOLS.index(msg[i])\ast len(SYMBOLS{)}^i$$

公匙密码算法进行加密解密过程

基于前面两小节的介绍，我们已经可以将字符串转化为分组了。我们可以使用公钥密码算法的一般方程：
$$\begin{gathered} C=M^{e}modn \\ M=C^{d}modn \end{gathered}$$
第一个等式用于加密整数分组，第二个等式用于解密。M代表明文消息分组，C代表密文消息分组。数字e和n组成了用于加密的公钥，数字d和n组成了密钥。数据的发送方可以发送公钥(e,n),让消息的接受方用公钥进行加密.

分组转换为字符串

我们可以使用私钥对收到的密文进行解密得到明文的分组信息，记明文分组信息为blockInteger。后面我们还需要做的是将明文分组转化为原始字符串。

将分组转化为字符串的过程是字符转化为分组的逆过程。转化的过程可以参考以下伪代码：

s := ""
for i in range(len(str), 0):
	if blockInteger / len(SYMBOLS)**i == 0:
		continue
	s += SYMBOLS[ blockInteger // (len(SYMBOLS)**i)]
	blockInteger = blockInteger / len(SYMBOLS)**i
aimStr = reverse(s)

---

关于公钥和私钥的生成及原理可以参考 文章.

混合密码体制

RSA和公钥密码需要非常长的时间来完成计算，对于需要每秒与其他计算机建立数千个加密连接的服务器来说，这个过程的时间过长。因此出现了一种解决方案，因为对称密码的速度更快，所以人们可以使用公钥密码来加密和分发对称密码的密钥，只要这一种对称密码的解密和加密使用相同的密钥即可。通过公钥密码加密对称密码的密钥，将其安全地发送给接收者之后，发送者就可以用对称密码加密之后的消息。结合使用对称密码和非对称密码进进行通信，称为混合密码体制。

混合密码体制的出现是巧妙的 出现的过程是顺畅的。

公钥密码体制的低速性但却更好地保证了信息安全性， 对称密码速度快但是密钥共享过程比较麻烦。 混合密码体制就将两者结合吸收了两者的优点。

部分代码实现

下面实现了前面提到的几种加密方式（并没有全部实现）,

from math import gcd

def encodeCaesarItem(itemCode, mod, symbols, key):
  """
    ## 使用凯撒密码的方式编码其中的一个字符
  """
  aimCode = itemCode
  if itemCode in symbols:
    codeIndex = symbols.find(itemCode)
    aimCode = symbols[(codeIndex - key) % len(symbols)] if mod else symbols[(codeIndex + key) % len(symbols)]
  return aimCode

def get_multiplicative_inverse(a, maxLen):
  """
    ## 遍历获得a的乘法逆元
  """
  for i in range(1, maxLen):
    if a * i % maxLen == 1:
      return i


def encodeAffineItem(itemCode, mod, symbols, multipleKey, shiftKey):
  """
    ## 仿射密码编码的方式编码其中的一个字符
  """
  aimCode = itemCode
  if itemCode in symbols:
    codeIndex = symbols.find(itemCode)
    aimCode = symbols[(codeIndex * multipleKey  - shiftKey) % len(symbols)] if mod else symbols[(codeIndex + shiftKey) * get_multiplicative_inverse(multipleKey, len(symbols))  % len(symbols)]
    return aimCode

class Cryptology:
  SYMBOLS = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz12345!?."
  """
    ## 记录几种加密算法
  """
  @classmethod
  def reverseCipher(self, str):
    """
      ## 反向密码
      - ``param: str`` 待加密字符串
    """
    return str[-1::-1]
  
  @classmethod
  def caesarCipher(self, str, key, mod=False):
    """
      ## 凯撒密码
      - ``param: str`` 待加密字符串
      - ``param: key`` 加密解密用的密匙
      - ``param: mod``  False 为加密  True为解密
    """

    return "".join([encodeCaesarItem(i, mod=mod, symbols=self.SYMBOLS, key = key) for i in str])
  
  @classmethod
  def transpositionEncrypt(self, str, key):
    """
      ## 置换密码
    """
    ciphertext = [""] * key
    for column in range(key):
      currentIndex = column
      while currentIndex < len(str):
        ciphertext[column] += str[currentIndex]
        currentIndex += key
    return "".join(ciphertext)
  
  @classmethod
  def affineCipher(self, str, multipleKey, shiftKey, mod=False):
    """
      ## 仿射密码
      - ``param: str`` 待加密字符串
      - ``param: multipleKey`` 用于乘法密码部分的乘法密匙
      - ``param: shiftKey`` 用于凯撒密码部分的移位密匙
      - ``param: mod`` False 为编码 True为解码
    """
    assert gcd(len(self.SYMBOLS), multipleKey) == 1, "Invalid multipleKey key"
    return "".join([encodeAffineItem(i, symbols=self.SYMBOLS, multipleKey=multipleKey, shiftKey=shiftKey, mod=mod) for i in str])


def test():
  message = "yncRG4s"
  # message = ".GNUbip"
  print(Cryptology.affineCipher(message, 7, 3, mod=False))

if __name__ == '__main__':
  test()

小结

本文参考: 《Python密码学编程》