codetop
链表题型
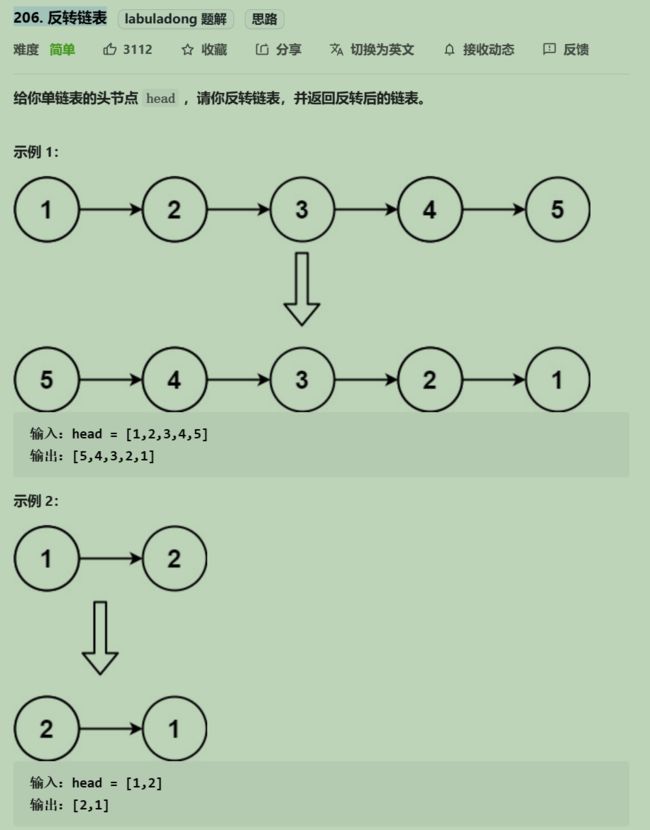
206 反转链表
递归:从函数的定义参数来看,别跳进去
92.反转链表II
//递归条件反转前n个节点,用后继节点记录,再反转中间区间的节点,改变链表指向
class Solution {
public:
ListNode* reverseBetween(ListNode* head, int left, int right) {
if(left == 1){
return reserve(head,right);//反转前right个节点
}
ListNode* tmp = reverseBetween(head->next,left-1,right-1);//left,right 都表示坐标
head->next = tmp;
return head;
}
//反转前right个节点
ListNode* suc = nullptr;//后继节点
ListNode* reserve(ListNode* head,int right){
if(right == 1 ){
suc = head->next; //记录后继节点 放在第right个的下一个位置
return head;
}
ListNode* tmp = reserve(head->next,right-1);//不要跳进递归,从定义看,反转后的头节点
head->next->next = head;
head->next = suc;
return tmp;
}
};
class Solution {
public:
ListNode* reverseBetween(ListNode* head, int left, int right) {
//条件为1时 反转前n个链表
if(left == 1) return reverse(head,right);
ListNode* tmp = reverseBetween(head->next,left-1,right-1);
head->next = tmp;
return head;
}
//反转链表前right个节点,+ 后继节点
ListNode* success = nullptr;
ListNode* reverse(ListNode* head,int right){
if(right == 1){
success = head->next;//head->next 空节点
return head;
}
ListNode* tmp = reverse(head->next,right-1);
head->next->next = head;
head->next = success;
return tmp;
}
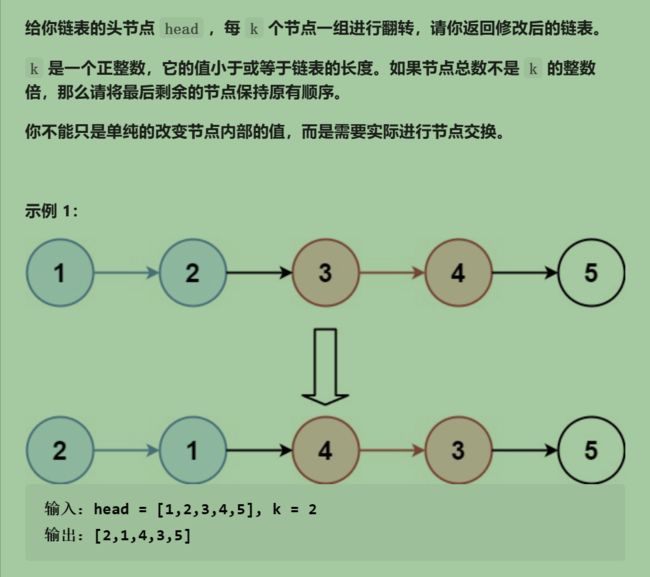
};25. K 个一组翻转链表
输入 head,reverseKGroup 函数能够把以 head 为头的这条链表进行翻转。
我们要充分利用这个递归函数的定义,把原问题分解成规模更小的子问题进行求解。
1、先反转以 head 开头的 k 个元素。 [a,b) reverse(a,b)
2、将第 k + 1 个元素作为 head 递归调用 reverseKGroup 函数。
将上述两个过程的结果连接起来。 a->next = reverseKGroup(b,k)
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
if(head == nullptr) return head;
//分为两个移动节点
ListNode* a = head;
ListNode* b = head;
for(int i = 0;i < k;i++){
if(b == nullptr) return a; // 小于等于k的长度不转化 return 原来的头节点
b = b->next;
}
ListNode* newHead = reverse(a,b); // 反转区间[a,b)
a->next = reverseKGroup(b,k); // 原a->next 下一个节点为递归的新节点
return newHead;
}
//反转 区间的节点 迭代法
ListNode* reverse(ListNode* a,ListNode* b){
//三个节点,前当后
ListNode* pre = nullptr;
ListNode* cur = a;
ListNode* nt = a;
while(cur != b){
nt = cur->next;
cur->next = pre;
pre = cur;
cur = nt;
}
return pre;//反转后的新头节点
}
};21. 合并两个有序链表
class Solution{
public:
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2){
if(list1 == NULL) return list2;
if(list2 == NULL) return list1;
if(list1->val <= list2->val){
list1->next = mergeTwoLists(list1->next,list2);//list1类似于头节点指针
return list1;
}else{
list2->next = mergeTwoLists(list1,list2->next);
return list2;
}
return NULL;
}
};
二叉树题型
124. 二叉树中的最大路径和
//最大路径和 当前根节点+左子树返回的最大值+右子树返回的最大值
//左子树有很多分支,需要取左子树的左右子树的最大分支值
class Solution{
public:
int result = INT_MIN;//很重要,不然通过不了!!!
//遍历整棵树,递归返回值需要处理,需要返回值,用左右变量接收,再中间逻辑处理 后序遍历(往上走)
int dfs(TreeNode* cur){
if(cur == NULL){
return 0;//遇到空节点 没有收益
}
int left = dfs(cur->left);//左子树的最大路径和 //根据return 返回的要么0,要么outresult 0已经考虑进去了
int right = dfs(cur->right);//右子树的最大路径和
//中间节点的处理
int inresult = cur->val + left + right;//当前子树根节点的内部最大路径和
//当前一个子树内部的路径,要包含当前子树的根节点 的路径和可能为最大,需要遍历比较每个根节点的最大路径和
result = max(result,inresult);
int outresult = cur->val + max(0,max(left,right));
//向外根节点提供左子树一条边的最大路径和
//当前根节点+左子树的一条边(取左右一边) + 右子树的一条边(取左右一边)
//左子树的一条边最大值(取左右一边) 返回给根节点
return max(outresult,0);//left/rght子树的一条边的最大值 返回给当前根节点
}
int maxPathSum(TreeNode* root){
if(root == NULL) return 0;
dfs(root);
return result;
}
};#include
#include
using namespace std;
// Definition for a binary tree node.
class TreeNode {
public:
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int val) : val(val), left(NULL), right(NULL) {}
};
class Solution {
public:
int result = INT_MIN;
int dfs(TreeNode* cur){
if(cur == NULL) return 0;
int left = dfs(cur->left);
int right = dfs(cur->right);
int inresult = cur->val + left + right; //内部最大路径和
result = max(result,inresult);
int outresult = cur->val + max(0,max(left,right));
//向外根节点提供左子树一条边的最大路径和
//当前根节点+左子树的一条边(取左右一边) + 右子树的一条边(取左右一边)
return outresult < 0 ? 0 : outresult;
//左子树的一条边最大值(取左右一边) 返回给根节点
}
int maxPathSum(TreeNode* root) {
if(root == nullptr) return 0;
dfs(root);
return result;
}
};
int main() {
// Create a binary tree manually
TreeNode* root = new TreeNode(-10);
root->left = new TreeNode(9);
root->right = new TreeNode(20);
root->right->left = new TreeNode(15);
root->right->right = new TreeNode(7);
Solution s;
int maxPathSum = s.maxPathSum(root);
cout << "The maximum path sum is: " << maxPathSum << endl;
// Clean up memory
delete root->right->right;
delete root->right->left;
delete root->right;
delete root->left;
delete root;
return 0;
}
199. 二叉树的右视图(广度优先遍历)
class Solution{
public:
vector rightSideView(TreeNode* root){
queue que;
if(root!=nullptr) que.push(root);
vector res;
while(!que.empty()){
int size = que.size();
for(int i = 0;ival);
if(node->left) que.push(node->left);
if(node->right) que.push(node->right);
}
}
return res;
}
}; #include
#include
#include
using namespace std;
// 树节点的结构定义
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
vector rightSideView(TreeNode* root) {
queue que;
if(root != nullptr) que.push(root);
vector result;
while(!que.empty()){
int size = que.size();
for(int i = 0;i < size;i++){
TreeNode* cur = que.front();
que.pop();
if(i == size-1) result.push_back(cur->val);
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
}
return result;
}
};
// main函数用于测试Solution的功能
int main() {
// 创建一棵测试用的二叉树
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->left->right = new TreeNode(5);
root->right = new TreeNode(3);
root->right->right = new TreeNode(4);
// 测试Solution的rightSideView函数
Solution solution;
vector result = solution.rightSideView(root);
// 输出结果
for(int i = 0;i < result.size();i++){
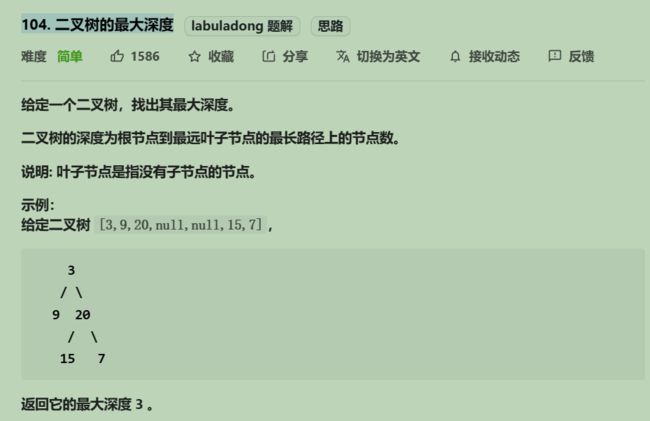
cout< 104. 二叉树的最大深度
//当前节点递归 求根节点的高度 就是二叉树的最大深度,后序遍历(左右中)
class Solution{
public:
int maxDepth(TreeNode* root){
if(root==NULL) return 0;
int left = maxDepth(root->left);
int right = maxDepth(root->right);
int depth = 1 + max(left,right);
return depth;
}
};#include
using namespace std;
// 声明二叉树节点结构体
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution{
public:
int maxDepth(TreeNode* root){
if(root==NULL) return 0;
int left = maxDepth(root->left);
int right = maxDepth(root->right);
int depth = 1 + max(left,right);
return depth;
}
};
int main() {
// 构造二叉树
TreeNode* root = new TreeNode(3);
root->left = new TreeNode(9);
root->right = new TreeNode(20);
root->right->left = new TreeNode(15);
root->right->right = new TreeNode(7);
// 计算二叉树深度
Solution solution;
int depth = solution.maxDepth(root);
// 输出结果
cout << "The depth of the binary tree is: " << depth << endl;
// 释放内存
delete root->left;
delete root->right->left;
delete root->right->right;
delete root->right;
delete root;
return 0;
}
110. 平衡二叉树
//高度差 先求高度,后序遍历(中间处理)
class Solution {
public:
int getHeight(TreeNode* node){
if(node == NULL){
return 0;
}
int leftHeight = getHeight(node->left);
//若返回的是-1,说明不是平衡二叉树,早点结束
if(leftHeight==-1){
return -1;
}
int rightHeight = getHeight(node->right);
if(rightHeight==-1){
return -1;
}
//高度是根节点到叶子节点的最长路径
return abs(leftHeight-rightHeight)>1 ? -1 : 1+max(leftHeight,rightHeight);
}
bool isBalanced(TreeNode* root) {
return getHeight(root)==-1 ? false:true;
}
};#include
#include
#include
using namespace std;
// Definition for a binary tree node.
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
int getHeight(TreeNode* node){
if(node == NULL){
return 0;
}
int leftHeight = getHeight(node->left);
//若返回的是-1,说明不是平衡二叉树,早点结束
if(leftHeight==-1){
return -1;
}
int rightHeight = getHeight(node->right);
if(rightHeight==-1){
return -1;
}
//高度是根节点到叶子节点的最长路径
return abs(leftHeight-rightHeight)>1 ? -1 : 1+max(leftHeight,rightHeight);
}
bool isBalanced(TreeNode* root) {
return getHeight(root)==-1 ? false:true;
}
};
int main() {
Solution s;
TreeNode *root = new TreeNode(3);
root->left = new TreeNode(9);
root->right = new TreeNode(20);
root->right->left = new TreeNode(15);
root->right->right = new TreeNode(7);
bool result = s.isBalanced(root);
cout << result << endl;
return 0;
}
129. 求根节点到叶节点数字之和
class Solution {
public:
int dfs(TreeNode* root,int preNum){
if(root==nullptr){
return 0;
}
int sum = preNum*10 + root->val;
if(root->left == nullptr && root->right == nullptr){
return sum;
}else{
//dfs(根节点左节点,根节点和)
return dfs(root->left,sum) + dfs(root->right,sum);
}
}
int sumNumbers(TreeNode* root) {
return dfs(root,0);
}
};#include
#include
#include
#include
#include
using namespace std;
// 定义二叉树节点结构体
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
int dfs(TreeNode* root,int preNum){
if(root==nullptr){
return 0;
}
int sum = preNum*10 + root->val;
if(root->left == nullptr && root->right == nullptr){
return sum;
}else{
//dfs(根节点左节点,根节点和)
return dfs(root->left,sum) + dfs(root->right,sum);
}
}
int sumNumbers(TreeNode* root) {
return dfs(root,0);
}
};
int main() {
// 输入二叉树的先序遍历序列
string preorderStr;
getline(cin, preorderStr);
// 将先序遍历序列转换为vector类型
vector preorderVec;
istringstream iss(preorderStr);
int num;
while (iss >> num) {
preorderVec.push_back(num);
}
// 重建二叉树
TreeNode *root = nullptr;
vector treeNodes(preorderVec.size());
for (int i = 0; i < preorderVec.size(); i++) {
if (preorderVec[i] != -1) {
treeNodes[i] = new TreeNode(preorderVec[i]);
} else {
treeNodes[i] = nullptr;
}
}
for (int i = 1; i < treeNodes.size(); i++) {
if (treeNodes[i] == nullptr) {
continue;
}
int parentIndex = (i - 1) / 2;
if (i % 2 == 1) {
treeNodes[parentIndex]->left = treeNodes[i];
} else {
treeNodes[parentIndex]->right = treeNodes[i];
}
}
root = treeNodes[0];
// 计算二叉树中所有根节点到叶子节点的路径之和
Solution s;
int result = s.sumNumbers(root);
// 输出结果
cout << result << endl;
return 0;
}
从标准输入中读入二叉树的先序遍历序列,例如1 2 3 -1 -1 4 5。
将先序遍历序列转换为vector类型,其中-1表示空节点。
根据先序遍历序列重建二叉树。
调用sumNumbers方法计算二叉树中所有根节点到叶子节点的路径之和。
将结果输出到标准输出中。
istringstream是C++标准库中的一个类,可以用于从一个字符串中读取数据,其构造函数可以接受一个字符串参数,将该字符串转换成一个类似于输入流的对象,可以通过输入运算符(>>)来从中读取数据。
在上述代码中,我们使用istringstream来将从标准输入中读取的字符串preorderStr转换成一个类似于输入流的对象iss,然后通过iss >> num语句来从中读取整数数据。这样就可以方便地将输入的先序遍历序列转换成一个vector类型的向量,便于后续的处理。 101. 对称二叉树
递归
// class Solution{
// public:
// bool mycompare(TreeNode* left,TreeNode* right){
// if(left==nullptr&&right==nullptr) return true;
// else if(left==nullptr || right==nullptr || (left->val != right->val)) return false;
//递归 下下层
// bool outside = mycompare(left->left,right->right);
// bool inside = mycompare(left->right,right->left);
// return outside&&inside;
// }
// bool isSymmetric(TreeNode* root){
// if(root == nullptr) return true;
// return mycompare(root->left,root->right);
// }
// };
class Solution{
public:
bool isSymmetric(TreeNode* root){
if(root==nullptr) return true;
queue que;
que.push(root->left);
que.push(root->right);
while(!que.empty()){
TreeNode* leftNode = que.front();que.pop();
TreeNode* rightNode = que.front();que.pop();
if(!leftNode && !rightNode) continue;
if(!leftNode || !rightNode || (leftNode->val != rightNode->val)) return false;
//空节点放进去考虑
que.push(leftNode->left);
que.push(rightNode->right);
que.push(leftNode->right);
que.push(rightNode->left);
}
return true;
}
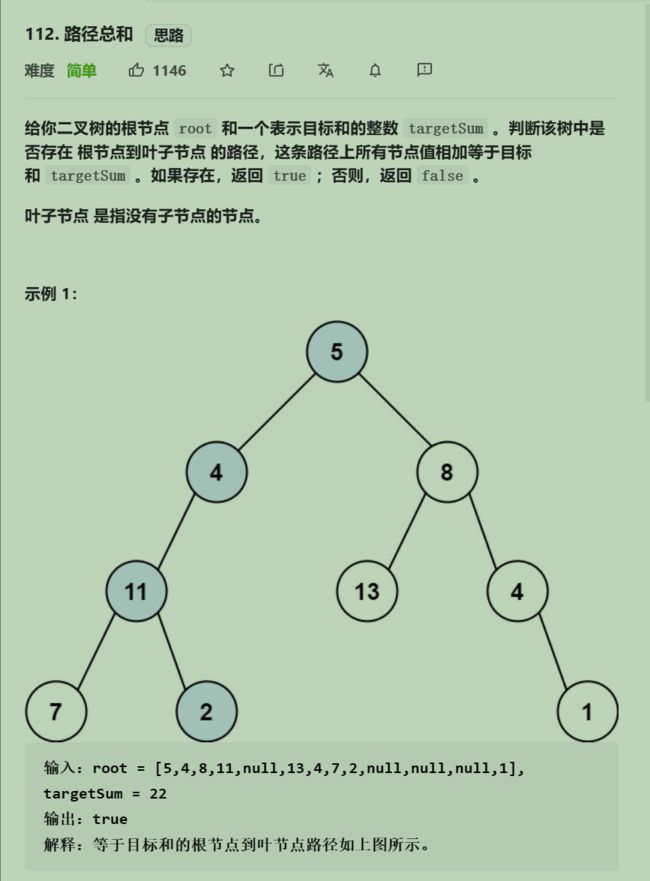
}; 112. 路径总和
//递归+回溯
class Solution{
public:
//遍历某条固有路径,需要返回值
bool traversal(TreeNode* node,int count){
if(!node->left && !node->right && count == 0) return true;
//左右孩子为空且 反向计数器为零
if(!node->left && !node->right) return false;//单独为叶子节点
//左
if(node->left){
//先减再递归
count -= node->left->val;
if(traversal(node->left,count)) return true;//if为真,找到了
count += node->left->val;//没找到,回溯到右边找
}
//右
if(node->right){
count -= node->right->val;
if(traversal(node->right,count)) return true;//中
count += node->right->val;
}
return false;//对比完全部的,仍然没找到
}
bool hasPathSum(TreeNode* root,int targetSum){
if(root==NULL) return false;
return traversal(root,targetSum-root->val);
//targetSum-root->val 中间节点的处理 中左右(自顶向下) 一节点到另一节点
//可以用递减,让计数器count初始为目标和,然后每次减去遍历路径节点上的数值。
}
};
//迭代法
// class Solution{
// public:
// bool hasPathSum(TreeNode* root,int targetSum){
// if(root == NULL) return false;
// stack> st;
// st.push(pair(root,root->val));
// while(!st.empty()){
// //栈的前序遍历
// pair node = st.top();
// st.pop();
// if(!node.first->left&&!node.first->right&&targetSum==node.second) return true; //遇到叶子节点,此时的值为目标和
// if(node.first->right){//右
// st.push(pair(node.first->right,node.second+node.first->right->val));
// }
// if(node.first->left){//左
// st.push(pair(node.first->left,node.second+node.first->left->val));
// }
// }
// return false;
// }
// }; 113. 路径总和 II
class Solution {
public:
vector> result;
vector path;
void traversal(TreeNode* root,int count){
if(!root->left && !root->right && count == 0){
result.push_back(path);
}
if(!root->left && !root->right){
return;
}
if(root->left){
path.push_back(root->left->val);
count -= root->left->val;
traversal(root->left,count); //没找到 回溯跳出
count += root->left->val;
path.pop_back();
}
if(root->right){
path.push_back(root->right->val);
count -= root->right->val;
traversal(root->right,count);
count += root->right->val;
path.pop_back();
}
return ;
}
vector> pathSum(TreeNode* root, int targetSum) {
if(root == nullptr ) return result;
path.push_back(root->val);
traversal(root,targetSum-root->val);
return result;
}
}; 98. 验证二叉搜索树
class Solution {
public:
vector res;
//中序遍历递归 存放到 res 数组
void traversal(TreeNode* root){
if(root == NULL) return;
if(root->left) traversal(root->left);
res.push_back(root->val);
if(root->right) traversal(root->right);
}
bool isValidBST(TreeNode* root) {
traversal(root);
for(int i = 0;i < res.size()-1;i++){
if(res[i] >= res[i+1]) return false;
}
return true;
}
}; 105. 从前序与中序遍历序列构造二叉树
class Solution {
public:
TreeNode* traversal(vector& preorder,int preorderbegin,int preorderend,vector& inorder,int inorderbegin,int inorderend){
if(preorderend==preorderbegin) return nullptr;
int rootvalue = preorder[preorderbegin];
TreeNode* root = new TreeNode(rootvalue);
if(preorderend-preorderbegin == 1) return root;
int delimiterIndex ;
for(delimiterIndex=inorderbegin;delimiterIndexleft = traversal(preorder,leftpreorderbegin,leftpreorderend,inorder,leftinorderbegin,leftinorderend);
root->right = traversal(preorder,rightpreorderbegin,rightpreorderend,inorder,rightinorderbegin,rightinorderend);
return root;
}
TreeNode* buildTree(vector& preorder, vector& inorder) {
if(preorder.size()==0 || inorder.size()==0) return nullptr;
return traversal(preorder,0,preorder.size(),inorder,0,inorder.size());
}
}; 106. 从中序与后序遍历序列构造二叉树
class Solution {
public:
TreeNode* traversal(vector& inorder,vector& postorder){
//递归条件
if(postorder.size()==0) return nullptr;
//找到当前中间节点
int rootvalue = postorder[postorder.size()-1];
TreeNode* root = new TreeNode(rootvalue);
//递归条件
if(postorder.size()==1) return root;
//找到中序的切割点
int delimiterIndex ;
for( delimiterIndex = 0;delimiterIndex leftinorder(inorder.begin(),inorder.begin()+delimiterIndex);
vector rightinorder(inorder.begin()+delimiterIndex+1,inorder.end());
//舍弃后序的末尾元素
postorder.resize(postorder.size()-1);
//切割后序数组
//[0,leftinorder.size())
vector leftpostorder(postorder.begin(),postorder.begin()+leftinorder.size());
vector rightpostorder(postorder.begin()+leftinorder.size(),postorder.end());
//此时有了根节点root,左右数组都分割好了,重新递归 左右数组
root->left = traversal(leftinorder,leftpostorder);
root->right = traversal(rightinorder,rightpostorder);
return root;
}
TreeNode* buildTree(vector& inorder, vector& postorder) {
if(inorder.size()==0 || postorder.size()==0){
return nullptr;
}
return traversal(inorder,postorder);
}
}; 114. 二叉树展开为链表
class Solution{
public:
void flatten(TreeNode* root){
while(root!=NULL){
if(root->left == nullptr){
root = root->right;
}else{
TreeNode* pre= root->left;
while(pre->right != NULL){
pre = pre->right;//核心 : 先找到当前节点左孩子的最右节点
}
pre->right = root->right;//当前节点左孩子的最右节点 接上原来的右孩子
//当前节点的右左处理
root->right = root->left;
root->left = NULL;
root = root->right;//原来当前节点的右孩子 为新根节点,开始循环
}
}
}
};111. 二叉树的最小深度
// 层序遍历,广度优先遍历
//递归:不要跳入递归,就只想他的结果,
// 比如求根节点的最小深度,
// int left = minDepth(左孩子) left 就是左孩子最小深度
// 我们默认只拿到这个结果(左孩子最小深度)就可以
// 再放进中间处理逻辑
class Solution{
public:
int minDepth(TreeNode* root){
queue que;
if(root!=nullptr) que.push(root);
int depth = 0;
while(!que.empty()){
int size = que.size();
depth++;
for(int i = 0;ileft) que.push(node->left);
if(node->right) que.push(node->right);
if(node->left==nullptr && node->right==nullptr){
return depth;
}
}
}
return depth;
}
}; 100. 相同的树
//递归
// class Solution{
// public:
// bool isSame(TreeNode* left,TreeNode* right){
// if(left==NULL && right == NULL) return true;
// if(left==NULL|| right == NULL || (left->val != right->val)) return false;
// bool outside = isSame(left->left,right->left);//左左,右右
// bool inside = isSame(left->right,right->right);
// bool result = outside && inside;
// return result;
// }
// bool isSameTree(TreeNode* p,TreeNode* q){
// return isSame(p,q);
// }
// };
//迭代
class Solution{
public:
bool isSameTree(TreeNode* p,TreeNode* q){
if(p == NULL&& q == NULL) return true;
else if(p == NULL||q == NULL) return false;
queue que;
que.push(p);
que.push(q);
while(!que.empty()){
TreeNode* leftNode = que.front();que.pop();
TreeNode* rightNode = que.front();que.pop();
if(leftNode == NULL && rightNode == NULL) continue;//排在前
if(!leftNode || !rightNode || (leftNode->val!=rightNode->val)) return false;
que.push(leftNode->left); //左左,右右的放进
que.push(rightNode->left);
que.push(leftNode->right);
que.push(rightNode->right);
}
return true;
}
}; 108. 将有序数组转换为二叉搜索树
class Solution {
public:
//区间里递归
//递归的定义:将有序数组转化为二叉搜索树
TreeNode* traversal(vector& nums,int left ,int right){
if(left > right) return nullptr;
int mid = left + (right-left)/2; //有序的取中间为根节点
TreeNode* root = new TreeNode(nums[mid]);
//左孩子接住 递归 左区间(二叉搜索树)
root->left = traversal(nums,left,mid-1);
root->right = traversal(nums,mid+1,right);
return root;
}
TreeNode* sortedArrayToBST(vector& nums) {
TreeNode* root = traversal(nums,0,nums.size()-1);
return root;
}
}; 257. 二叉树的所有路径
递归+回溯
class Solution {
public:
//所有路径不用返回值,前序遍历,回溯
//vector& path,vector& result 一定要带引用
void traversal(TreeNode* node,vector& path,vector& result){
path.push_back(node->val);
if(node->left == nullptr && node->right == nullptr){
string rpath;
//遍历整型路径 转化为字符串路径
for(int i = 0;ileft){
//往下递归,往回走
traversal(node->left,path,result);
path.pop_back(); // 对应前面的path.push_back(node->val); 往路径添加一个必有回溯删除一个
}
if(node->right){
traversal(node->right,path,result);
path.pop_back();
}
}
vector binaryTreePaths(TreeNode* root) {
vector result;
//遍历路径收集
vector path;
if(root == nullptr) return result;
traversal(root,path,result);
return result;
}
}; 863. 二叉树中所有距离为 K 的结点
分离两颗树,分别求深度为K,K-1的问题
class Solution {
public:
vector result;
TreeNode* ne; //代表新树的根节点
vector distanceK(TreeNode* root, TreeNode* target, int k) {
dfs(root,NULL,target);//首先把树分成两棵,一棵以目标节点为根,一棵以目标节点爸爸为根
cal_chai(target,0,k);//搜索第一棵树深度为K的节点
cal_chai(ne,0,k-1);//搜索第二棵树深度为K-1的节点
return result;
}
bool dfs(TreeNode* cur,TreeNode* cur_father,TreeNode* target){
if(cur == NULL)
return 0;
if(cur == target){ //当前节点为目标点,其父节点为新树的根节点
ne = cur_father;
return 1;
}
if(dfs(cur->left,cur,target)){ //当前节点不为目标点,左子树找到目标点 且ne为新树的根节点
cur->left = cur_father; //当前节点的左孩子设置为 其父节点(新的儿子)(父节点为根节点的树) 分离操作
return 1;
}
if(dfs(cur->right,cur,target)){
cur->right = cur_father;
return 1;
}
return 0;
}
void cal_chai(TreeNode* root,int n,int k){
if(root == NULL)
return;
if(n == k){
result.push_back(root->val);
}else{
cal_chai(root->left,n+1,k);
cal_chai(root->right,n+1,k);
}
return;
}
}; 排序题型
912. 排序数组
快速排序/插入排序
双路快排 + 小区间插入快排
双路快排:把等于切分元素的所有元素等概率地分到了数组的两侧,避免了递归树倾斜,递归树相对平衡
只partition没有合
#define insert 7
class Solution {
public:
vector sortArray(vector& nums) {
int len = nums.size();
quickSort(nums,0,len-1);
return nums;
}
void quickSort(vector& nums,int left,int right){
if(right-left <= insert){
insertionSort(nums,left,right);//插入排序
return;
}
int pIndex = partition(nums,left,right);//二路快排划分 返回
quickSort(nums,left,pIndex-1);
quickSort(nums,pIndex+1,right);
}
//小区间 插入排序
void insertionSort(vector& nums,int left,int right){
for(int i = left+1;i <= right;i++){
int temp = nums[i];
int j = i;
while(j > left && nums[j-1] > temp){
nums[j] = nums[j-1];
j--;
}
nums[j] = temp;
}
}
//双路快排
int partition(vector & nums,int left ,int right){
srand((unsigned)time(NULL));
int ranidx = left + rand() % (right-left+1);
swap(nums[left],nums[ranidx]); //交换随机数,左边为随机数
int mid = nums[left];
int lt = left + 1;
int gt = right;
while(true){
// 循环不变量:
// all in [left + 1, lt) <= mid
// all in (gt, right] >= mid
while(lt <= gt && nums[lt] < mid){
lt++;
}
while(lt <= gt && nums[gt] > mid){
gt--;
}
if(lt >= gt) break;
//此时gt在lt左边,交换位置,大的放右边,等概率分到数组两边
swap(nums[lt],nums[gt]);
//新一轮
lt++;
gt--;
}
swap(nums[left],nums[gt]); //交换位置,让nums[left]在中间平衡两端
return gt;//返回中间排好的下标
}
};
//时间复杂度O(NlogN) 空间复杂度O(logN) 占用的空间主要来自递归函数的栈空间
//不懂看weiwei https://www.bilibili.com/video/BV1jB4y117GJ/?spm_id_from=333.788 深度优先搜索题型
岛屿题型
200. 岛屿数量
思路:遍历到岛屿,dfs,边界判定,标志为已遍历,避免重复递归,当前点四周遍历
class Solution {
public:
int numIslands(vector>& grid) {
int count = 0;
for(int i = 0;i < grid.size();i++){
for(int j = 0;j >& grid,int x,int y){
if(x < 0 || y < 0 || x >= grid.size() || y >= grid[0].size() || grid[x][y] != '1'){
return;//边界,访问到标识过的
}
grid[x][y] = '2';//遇到岛屿,1变2 为标识 避免重复递归
//当前点 递归四方向
dfs(grid,x-1,y);
dfs(grid,x+1,y);
dfs(grid,x,y-1);
dfs(grid,x,y+1);
}
}; #include
#include
using namespace std;
void dfs(vector>& grid, int i, int j) {
int m = grid.size();
int n = grid[0].size();
if (i < 0 || i >= m || j < 0 || j >= n || grid[i][j] == 0) {
return;
}
grid[i][j] = 0;
dfs(grid, i + 1, j);
dfs(grid, i - 1, j);
dfs(grid, i, j + 1);
dfs(grid, i, j - 1);
}
int numIslands(vector>& grid) {
if (grid.empty()) {
return 0;
}
int m = grid.size();
int n = grid[0].size();
int count = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
count++;
dfs(grid, i, j);
}
}
}
return count;
}
int main() {
int m, n;
cout << "请输入矩阵的行数和列数:";
cin >> m >> n;
vector> grid(m, vector(n));
cout << "请输入矩阵每个位置的值:" << endl;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
cin >> grid[i][j];
}
}
int count = numIslands(grid);
cout << "岛屿数量为:" << count << endl;
return 0;
} 695. 岛屿的最大面积
class Solution {
public:
int maxAreaOfIsland(vector>& grid) {
int res = 0;
for(int i = 0;ires ? a : res ;
}
}
}
return res;
}
int areadfs(vector>& grid,int x,int y){
if(x<0 || y<0 || x>= grid.size() || y>= grid[0].size() || grid[x][y] != 1){
return 0;
}
grid[x][y] = 2;
return 1 + areadfs(grid,x-1,y) + areadfs(grid,x+1,y) + areadfs(grid,x,y+1) + areadfs(grid,x,y-1);
//1表示当前为岛屿的一格算1面积,然后递归四个方向的面积
}
}; 463. 岛屿的周长
class Solution {
public:
int islandPerimeter(vector>& grid) {
for(int i = 0;i>& grid,int x,int y){
if(x<0 || x>=grid.size() || y<0 || y>=grid[0].size() || grid[x][y] == 0) {
return 1;//遇到边界,海格 加1
}
if(grid[x][y] != 1){
return 0;//没遇到岛屿
}
grid[x][y] = 2;//标识遇到过岛屿 1 变 2
return dfs(grid,x-1,y) + dfs(grid,x+1,y) + dfs(grid,x,y-1) + dfs(grid,x,y+1);//再递归四个方向
}
}; 1020. 飞地的数量
class Solution {
public:
vector> da = {{1,0},{-1,0},{0,1},{0,-1}};
int numEnclaves(vector>& grid) {
vector> res(grid.size(),vector(grid[0].size(),false));
for(int i = 0;i>& grid,int row,int col,vector>& res){
if(row<0 || row>=grid.size() || col<0 || col>=grid[0].size() || res[row][col] == 1 || grid[row][col] ==0 ){
return ;// res[row][col] == 1 || grid[row][col] ==0 走四个方向时 陆地标识过或者遇到海格 (相当于遇到叶子节点都返回)
}
res[row][col] = 1;//标识陆地用过 连贯性
for(auto d : da){
dfs(grid,row + d[0],col + d[1],res);//四个方向
}
}
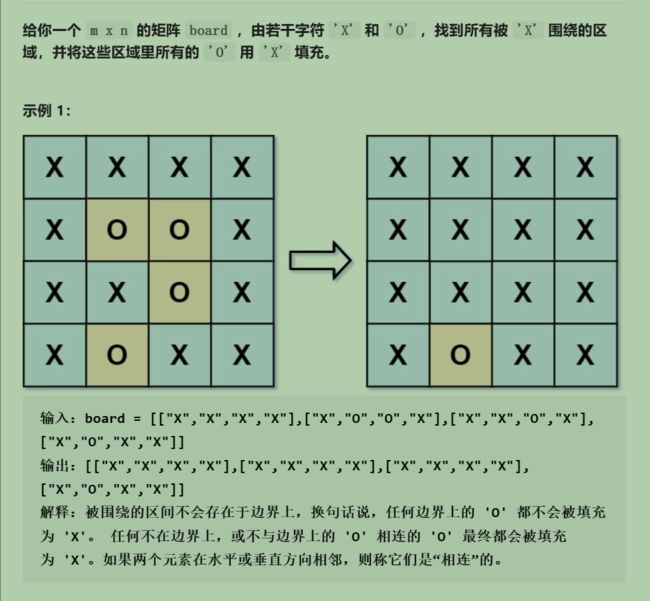
}; 130. 被围绕的区域
飞地题型差不多
class Solution {
public:
vector> da = {{-1,0},{1,0},{0,1},{0,-1}};
void solve(vector>& board) {
int m = board.size();
int n = board[0].size();
vector> sign(m,vector(n,false));
for(int i = 0;i>& board,int x,int y,vector>& sign){
if(x <0 || x>=board.size() || y<0 || y>=board[0].size() || board[x][y] == 'X' || sign[x][y] == 1){
return ;
}
sign[x][y] = true;
for(auto d : da){
dfs(board,x+d[0],y+d[1],res);
}
}
}; 827. 最大人工岛
//先求岛屿各面积,再求合并面积 看题解的图示
class Solution {
public:
unordered_map map;// 是岛屿的前提下 key 岛屿编号,value 岛屿面积
int area = 0;
//计算岛屿的面积
void dfs(vector>& grid,int index,int x,int y){
if(x<0 || x>=grid.size() || y<0 || y>=grid[0].size() || grid[x][y] != 1){
return ;
}
grid[x][y] = index;//遇到岛屿 更新岛屿编号 后续合并面积接口用处
area += 1;
dfs(grid,index,x-1,y);
dfs(grid,index,x+1,y);
dfs(grid,index,x,y-1);
dfs(grid,index,x,y+1);
}
int largestIsland(vector>& grid) {
int res = 0;
int index = 2;
for(int i = 0;i> da = {{-1,0},{1,0},{0,1},{0,-1}};
for(int i = 0;i set;//去重,插入重复的值不加入
int cur_area = 1;//当前 grid[i][j] == 0 要变1的 面积
for(auto& d : da){//d为一维数组
int x = i + d[0];//i,j 坐标四个方向
int y = j + d[1];
if(x>=0&&x=0&&y DFS+记忆化题型
329. 矩阵中的最长递增路径
//利用dfs将深度优先搜索过程中得到matrix[i][j]的最长路径长度存储到memo[i][j]中
//然后如果memo[i][j]没有计算才需要dfs,否则说明已经计算过了就不用进一步计算
class Solution {
public:
vector> dir{{-1,0},{1,0},{0,1},{0,-1}};
vector> memo; //记忆化搜索用
int longestIncreasingPath(vector>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
if(m <= 0 || n <= 0) return 0;
memo.resize(m,vector(n,0)); //初始化用
int ans = 0;
// 枚举每一个节点
for(int i = 0;i < m ;i++){
for(int j = 0;j < n;j++){
//记录最长的路径
ans = max(ans,dfs(matrix,i,j));
}
}
return ans;
}
//返回以matrix[i][j]为起点的最长递增路径
int dfs(vector>& matrix,int i,int j){
//记忆化搜索,已有的不再搜
//若之前搜索过了直接返回之前存储的最大长度
if(memo[i][j] != 0) return memo[i][j];
int m = matrix.size();
int n = matrix[0].size();
//以matrix[i][j]为起点的最长递增路径
int ans = 1;// 默认长度为1
for(auto d : dir){
int x = i + d[0];
int y = j + d[1];
if(x >= 0 && y >= 0 && x < m && y < n && matrix[x][y] > matrix[i][j]){
//选择当前位置(i,j) 的4个方向的最大路径的最大值作为ans
ans = max(ans,dfs(matrix,x,y)+1); //满足递增,在新的位置x,y递归
}
}
// 将以matrix[i][j]为起点的最长递增路径存储在memo[i][j]中
// 注意:在递归过程中将matrix[nextI,nextJ]为起点的最长路径都存储在memo了
memo[i][j] = ans;
//返回该最长路径长度
return memo[i][j];
}
};
// //深度优先搜索 出度为0 的入队 的拓扑排序
// //矩阵转化为 有向无环图 出度为0的值是最大值(递增路径)
// class Solution {
// public:
// vector> dir{{-1,0},{1,0},{0,-1},{0,1}};
// int longestIncreasingPath(vector>& matrix) {
// if(matrix.size() <= 0 || matrix[0].size() <= 0) return 0;
// vector> out(matrix.size(),vector(matrix[0].size())); //出度为0
// // 1. 计算每个节点的出度
// for(int i = 0;i < matrix.size();i++){
// for(int j = 0;j < matrix[0].size();j++){
// for(auto d : dir){
// int x = i + d[0];
// int y = j + d[1];
// if(x >= 0 && y >= 0 && x < matrix.size() && y < matrix[0].size() && matrix[x][y] > matrix[i][j]){
// out[i][j]++;
// }
// }
// }
// }
// // 2. 出度为0加入队列
// queue> qu;
// for(int i = 0;i < matrix.size();i++){
// for(int j = 0;j < matrix[0].size();j++){
// if(out[i][j] == 0) qu.push({i,j});
// }
// }
// int ans = 0;
// while(!qu.empty()){
// ans++; // 每次开始遍历,说明又开始新的一层BFS
// int size = qu.size();
// for(int j = 0;j < size;j++){
// vector res = qu.front();qu.pop();
// for(auto d : dir){
// int pre_x = res[0] + d[0];
// int pre_y = res[1] + d[1];
// if(pre_x >= 0 && pre_y >= 0 && pre_x < matrix.size() && pre_y < matrix[0].size() && matrix[pre_x][pre_y] < matrix[res[0]][res[1]]){
// if(--out[pre_x][pre_y] == 0){
// qu.push({pre_x,pre_y});
// }
// }
// }
// }
// }
// return ans;
// }
// }; DFS题型
394. 字符串解码(栈求解)
class Solution {
public:
string decodeString(string s) {
stack nums ;//数字栈
stack strs;//字符串栈
int num = 0;
string res = "";
for(int i = 0;i= '0' && s[i]<= '9'){
num = num*10 + s[i] - '0';//字符转数字
}else if((s[i] >= 'a'&&s[i] <= 'z') || (s[i]>='A'&&s[i]<='Z')){
res = res + s[i];//连续字母
}else if(s[i] == '['){//遇到[数字,字符串放进栈中
nums.push(num);
num = 0;
strs.push(res);
res = "";
}else{
int tmp = nums.top();
nums.pop();
for(int i = 0;i 679. 24 点游戏
class Solution {
public:
bool judgePoint24(vector& cards) {
vector res;
for(int num : cards){
res.push_back((double)num);
}
return backtracking(res);
}
bool backtracking(vector& res){
int n = res.size();
if(n == 1){
return abs(res[0] - 24) < 0.001; //递归边界处理
}
for(int i = 0;i < n-1;i++){
for(int j = i + 1;j < n;j++){
vector new_res;
for(int k = 0;k < n;k++){
if(k == i || k == j ) continue;
new_res.push_back(res[k]); //放第三,第四元素 进新的数组
}
bool valid = false;
// 标识变量isValid初始为 false,默认会执行||后面的递归。
// 一旦某个递归返回真,isValid就变为真,由于||的短路特性,后面的递归不会执行
//加法
new_res.push_back(res[i]+res[j]);
valid = valid || backtracking(new_res);
new_res.pop_back(); //回溯
//减法
new_res.push_back(res[i] - res[j]);
valid = valid || backtracking(new_res);
new_res.pop_back();
new_res.push_back( res[j] - res[i]);
valid = valid || backtracking(new_res);
new_res.pop_back();
//乘法
new_res.push_back( res[i] * res[j]);
valid = valid || backtracking(new_res);
new_res.pop_back();
//除法
if(res[j] != 0){
new_res.push_back( res[i]/res[j]);
valid = valid || backtracking(new_res);
new_res.pop_back();
}
if(res[i] != 0){
new_res.push_back( res[j]/res[i]);
valid = valid || backtracking(new_res);
new_res.pop_back();
}
if(valid) return true;
}
}
return false;
}
}; 广度优先搜索题型
拓扑排序题型
找到所有顶点中入度为0的顶点,并且入队
进入循环,取出队首的顶点v,将其邻居的入度-1,相当于此时把顶点 v 从图中删除,对于它的邻居入度就-1
然后将邻居中入度为0的顶点再入队
依次循环,并记录每次删除的顶点数目
有向无环图 转成 线性的排序
207. 课程表
//广度优先遍历
//入度数组:课号 0 到 n - 1 作为索引,通过遍历先决条件表求出对应的初始入度。
//邻接表:用哈希表记录依赖关系(也可以用二维矩阵,但有点大)
//key:课号
//value:依赖这门课的后续课(数组)
class Solution {
public:
bool canFinish(int numCourses, vector>& prerequisites) {
vector rudu(numCourses);//入度数组[1,0] 0->1 1入度为+1,1为索引下标
unordered_map> map;//邻接哈希表,依赖关系 key为当前课号,value为一维数组的后续课号,后续课号都依赖于当前课号的发生
//初始化 遍历
for(int i = 0;i4 后续课号
}
queue Qu;//入队是索引课号
for(int i = 0;i result = map[select];//记录所选课的后续课
for(int i = 0;i < result.size();i++){
rudu[result[i]]--;//后续课入度相应减一 result[i] 为后续课的索引下标
if(rudu[result[i]] == 0) Qu.push(result[i]);//后续课入度为0,放进队列 执行while
}
}
return (count == numCourses) ;//选课数 为 总课程
return false;
}
}; 210. 课程表 II
class Solution {
public:
vector findOrder(int numCourses, vector>& prerequisites) {
vector rudu(numCourses); //入度数组
unordered_map> map;//邻接表哈希 <当前课,后续课数组>
//初始化
for(int i = 0;i < prerequisites.size();i++){
rudu[prerequisites[i][0]]++;
map[prerequisites[i][1]].push_back(prerequisites[i][0]);
}
//队列
queue Qe;
for(int i = 0;i < numCourses;i++){
if(rudu[i] == 0) Qe.push(i); //入度为0 ,放进队列
}
vector ans;
while(!Qe.empty()){
int select_ID = Qe.front(); //所选当前课
Qe.pop();
ans.push_back(select_ID);
vector result = map[select_ID]; //入度为0的当前课 的后序课数组
for(int i = 0;i < result.size();i++){
rudu[result[i]]--; //选一门课,后序课入度各自减一
if(rudu[result[i]] == 0) Qe.push(result[i]); //新入度为0 入队
}
}
if(numCourses != ans.size()) return {};
return ans;
}
}; 329. 矩阵中的最长递增路径
//深度优先搜索 出度为0 的入队 的拓扑排序
//矩阵转化为 有向无环图 出度为0的值是最大值(递增路径)
//https://leetcode.cn/problems/longest-increasing-path-in-a-matrix/solution/tong-ge-lai-shua-ti-la-yi-ti-si-jie-bfs-agawl/
class Solution {
public:
vector> dir{{-1,0},{1,0},{0,-1},{0,1}};
int longestIncreasingPath(vector>& matrix) {
if(matrix.size() <= 0 || matrix[0].size() <= 0) return 0;
vector> out(matrix.size(),vector(matrix[0].size())); //出度为0
// 1. 计算每个节点的出度
for(int i = 0;i < matrix.size();i++){
for(int j = 0;j < matrix[0].size();j++){
for(auto d : dir){
int x = i + d[0];
int y = j + d[1];
if(x >= 0 && y >= 0 && x < matrix.size() && y < matrix[0].size() && matrix[x][y] > matrix[i][j]){
out[i][j]++;
}
}
}
}
// 2. 出度为0加入队列
queue> qu;
for(int i = 0;i < matrix.size();i++){
for(int j = 0;j < matrix[0].size();j++){
if(out[i][j] == 0) qu.push({i,j});
}
}
int ans = 0;
while(!qu.empty()){
ans++; // 每次开始遍历,说明又开始新的一层BFS
int size = qu.size();
for(int j = 0;j < size;j++){
vector res = qu.front();qu.pop();
for(auto d : dir){
int pre_x = res[0] + d[0];
int pre_y = res[1] + d[1];
// 如果比当前值更小,则出度减一,若出度为0就加入队列
if(pre_x >= 0 && pre_y >= 0 && pre_x < matrix.size() && pre_y < matrix[0].size() && matrix[pre_x][pre_y] < matrix[res[0]][res[1]]){
if(--out[pre_x][pre_y] == 0){
qu.push({pre_x,pre_y});
}
}
}
}
}
return ans;
}
}; 回溯(递归)题型
代码随想录
回溯算法理论基础
组合问题:N个数里面按一定规则找出k个数的集合
切割问题:一个字符串按一定规则有几种切割方式
子集问题:一个N个数的集合里有多少符合条件的子集
排列问题:N个数按一定规则全排列,有几种排列方式
棋盘问题:N皇后,解数独等等
所有回溯法的问题都可以抽象为树形结构
回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度,都构成的树的深度。
递归就要有终止条件,所以必然是一棵高度有限的树(N叉树)
回溯法模板:回溯三部曲
回溯函数模板返回值以及参数
void backtracking(参数)回溯函数终止条件
树中就可以看出,一般来说搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。
if (终止条件) {
存放结果;
return;
}回溯搜索的遍历过程
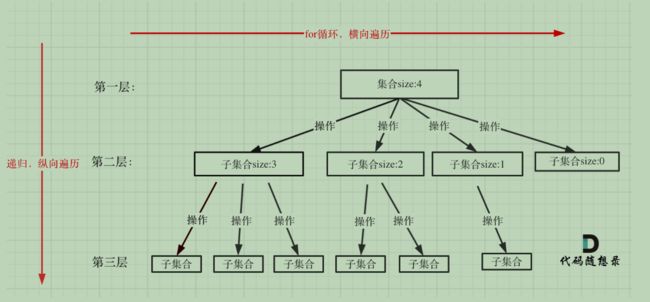
回溯法一般是在集合中递归搜索,集合的大小构成了树的宽度,递归的深度构成的树的深度
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}for循环就是遍历集合区间,可以理解一个节点有多少个孩子,这个for循环就执行多少次。
for循环可以理解是横向遍历,backtracking(递归)就是纵向遍历,这样就把这棵树全遍历完了,一般来说,搜索叶子节点就是找的其中一个结果了
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}组合题:需要startIndex来记录下一层递归,搜索的起始位置
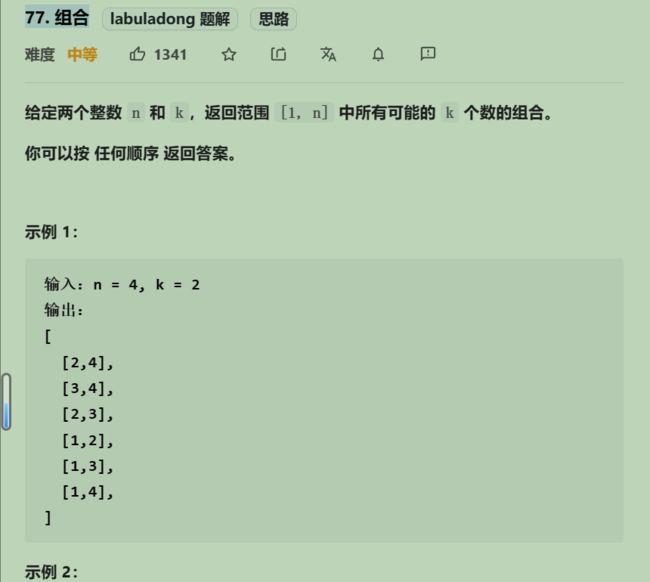
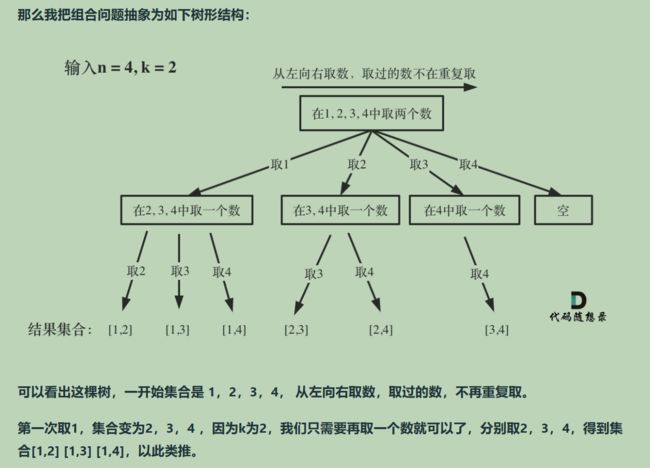
77. 组合
1234集合for 先取1,回溯后,从2开始遍历
需要startIndex来记录下一层递归,搜索的起始位置
class Solution {
public:
vector> result;
vector path;//已选择的元素个数
void backtracking(int n ,int k ,int startindex){
if(path.size() == k){
result.push_back(path);
return;
}
for(int i = startindex;i<= n-(k-path.size())+1;i++){
path.push_back(i);//横向遍历先取1个 处理节点
backtracking(n,k,i+1);//递归:控制树的纵向遍历,注意下一层搜索要从i+1开始
path.pop_back(); //回溯撤销当前节点
}
}
vector> combine(int n, int k) {
backtracking(n,k,1);
return result;
}
};
剪枝优化
已经选择的元素个数:path.size();
还需要的元素个数为: k - path.size();
在集合n中至多要从该起始位置 : n - (k - path.size()) + 1,开始遍历
为什么有个+1呢,因为包括起始位置,我们要是一个左闭的集合。
举个例子,n = 4,k = 3, 目前已经选取的元素为0(path.size为0),n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。
当前层for循环开始
class Solution {
public:
vector> result;
vector path;
void backtracking(int n,int k,int start_index){
if(path.size() == k){
result.push_back(path);
return;
}
for(int i = start_index;i <= n - (k-path.size()) + 1;i++){ //剪枝优化 后面遍历开始的数量少于我们需要的数量,剪枝不遍历
path.push_back(i); //处理 1
backtracking(n,k,i+1);
path.pop_back();
}
}
vector> combine(int n, int k) {
backtracking(n,k,1);
return result;
}
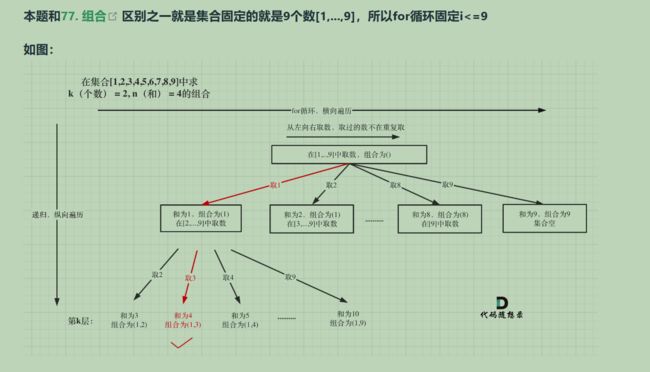
}; 216. 组合总和 III
class Solution{
public:
vector> result;
vector path;
void backtracking(int target,int k,int sum,int startindex){
//新加剪枝的操作(剪枝多了和超出,组合总和剪枝 只需要剪掉 集合个数,1234,k=4,若从2开始,只能234但凑不到四个数,剪枝)
if(sum > target){
return;//累加的和超过目标和,停止
}
if(path.size() == k){
if(sum == target) result.push_back(path);
return ;
}
//for循环的范围也可以剪枝
//for(int i = startindex;i <= 9;i++){
for(int i = startindex;i <= 9 -(k-path.size()) + 1;i++){
sum += i;
path.push_back(i);
backtracking(target,k,sum,i+1);//下一层递归的起始位置更新
//回溯
sum -= i;
path.pop_back();
}
}
vector> combinationSum3(int k, int n){
result.clear();
path.clear();
backtracking(n,k,0,1);
return result;
}
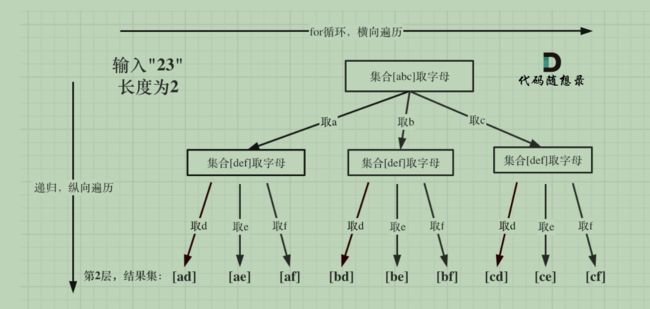
}; 17. 电话号码的字母组合
class Solution {
public:
string s;
vector result;
//枚举列出
const string lettermap[10] ={
"",//0
"",//1
"abc",//2
"def",//3
"ghi",//4
"jkl",//5
"mno",//6
"pqrs",//7
"tuv",//8
"wxyz",//9
};
void backtracking(string& digits,int startindex){
if(startindex == digits.size()){
result.push_back(s);
return;
}
//数字对应的字符串
int nums = digits[startindex] - '0';
string letter = lettermap[nums];
//i = startindex 错误
//跟77组合的区别 下一次递归i是从另外一个集合从头遍历
for(int i =0;i < letter.size();i++){
s.push_back(letter[i]);
//startindex+1 digit[1] 递归取第二种字符串
//i 为0 开始取
backtracking(digits,startindex+1); //非 i+1 取i可推理不对
s.pop_back();
}
}
vector letterCombinations(string digits) {
if(digits.size() == 0){
return result;
}
backtracking(digits,0);
return result;
}
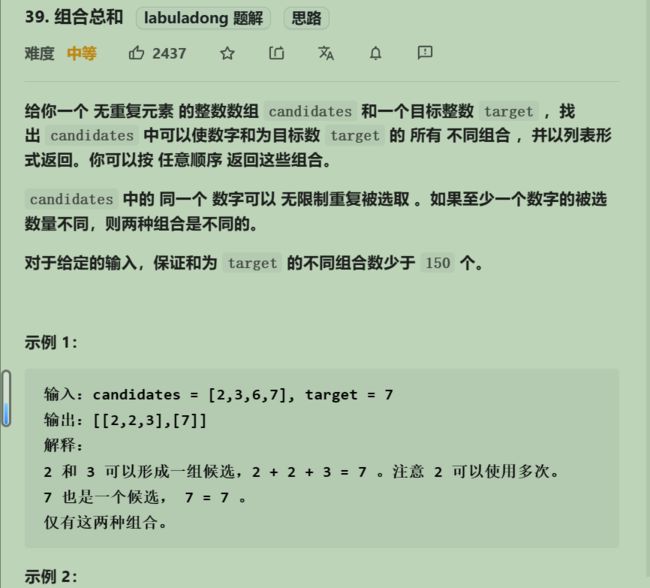
}; 39. 组合总和
横向遍历取了一次不能再重复取,纵向遍历取了一次可以重复取
在同一个集合取值,可以重复取(纵向递归遍历)
class Solution {
public:
vector> result;
vector path;
void backtracking(vector& candidates,int target,int sum,int index){
if(sum == target){//组合数量没有限制,不用path.size() == k
result.push_back(path);
return ;
}
//横向遍历不能重复取,for一次,每一次回溯,横向从下一个位置重新遍历
for(int i = index;i> combinationSum(vector& candidates, int target) {
sort(candidates.begin(),candidates.end());
backtracking(candidates,target,0,0);
return result;
}
};
40. 组合总和 II
集合里面有元素重复,需要used 横向遍历去重,纵向不用
结果集 只能使用一次集合元素,i+1 递归
class Solution {
public:
vector> result;
vector path;
void backtracking(vector& candidates,int target,int sum ,int index,vector& used){
if(sum == target){
result.push_back(path);
return;
}
for(int i = index;i0 && candidates[i] == candidates[i-1] && used[i-1] == false){
continue;
}
sum += candidates[i];
path.push_back(candidates[i]);
used[i] = true; //也要标志下
backtracking(candidates,target,sum,i+1,used); //i+1表示递归下一层不能重复取
path.pop_back();
sum -= candidates[i];
used[i] = false;
}
}
vector> combinationSum2(vector& candidates, int target) {
vector used(candidates.size(),0);
sort(candidates.begin(),candidates.end());
backtracking(candidates,target,0,0,used);
return result;
}
}; 131. 分割回文串
//分割 在同一集合求子串,要有切割线 startindex充当起始位置
class Solution{
public:
vector> result;
vector path;
void backtracking(string& s,int startindex){
//当切割线到了字符串末尾,就终止
if(startindex == s.size()){
result.push_back(path);
return ;
}
for(int i = startindex;i < s.size();i++){
//处理节点
//判断回文串,若是,取出在s的[startindex,i]的子串
if(isPalindrome(s,startindex,i)){
//substr(起始包括,个数)
string str = s.substr(startindex,i-startindex+1);
path.push_back(str);
}else{
continue;//ab 不是回文串,i+1,本层for循环,aba 是回文串,所以不用break
}
backtracking(s,i+1);//递归 i+1下一个切割位置
path.pop_back();
}
}
//判断回文串,双指针 会有重复计算,比如 [aa] [a,a] 最后遍历 子串b 都要遍历一次 对b双指针遍历
bool isPalindrome(string& s,int start,int end ){
for(int i = start,j = end;i> partition(string s){
result.clear();
path.clear();
backtracking(s,0);
return result;
}
}; 93. 复原 IP 地址
分割问题
//分割问题,回溯,startindex(在一个集合) ,pointNums记录 加逗号的 数量
class Solution{
public:
vector result;
void backtracking(string& s,int startindex,int pointNums){
//终止条件是 点的个数为3个,分割为四段
if(pointNums == 3){
//判断第四个子串是否合法
if(isValid(s,startindex,s.size()-1)){
result.push_back(s);
}
return ;
}
for(int i = startindex;i < s.size();i++){
//处理节点
//判断[startindex,i]在s的子串是否合法 合法再加点
if(isValid(s,startindex,i)){
s.insert(s.begin()+i+1,'.');//加逗号
pointNums++;//记录
backtracking(s,i+2,pointNums);//递归下一层 i+2位置取 不是i+1
//本来递归就要下一个位置,加了点 再推一个位置
pointNums--;
s.erase(s.begin()+i+1);//删除 下标 的 s.begin()+i+1 的'.'
}else break;//不合法,不用for找了
}
}
bool isValid(string& s,int start,int end){
if(start>end){
return false;
}
if(s[start] == '0' && start!=end){
return false;//start!=end 代表至少两个数,首个为0不合法,单独0 合法
}
int nums =0;
for(int i = start ;i<= end;i++){
if(s[i]>'9'||s[i]<'0') return false;//非法数字,在for里面,遍历每一个数
//从左到右将 字符串 变为数字,312 一开始 3 后31 再312
nums = nums*10+(s[i]-'0');
//255以后非法
if(nums>255) return false;
}
return true;//都不满足,说明合法
}
vector restoreIpAddresses(string s){
if(s.size()<4 || s.size() > 12) return result;//数量少于4 多于12 都不行
backtracking(s,0,0);
return result;
}
}; 78. 子集
遍历这个树的时候,把所有节点都记录下来,就是要求的子集集合
class Solution {
public:
vector> result;
vector path;
void backtracking(vector& nums,int index){
result.push_back(path); //所有的子集都收集
for(int i = index;i < nums.size();i++){
path.push_back(nums[i]);
backtracking(nums,i+1); //递归下一层,i+1不重复取
path.pop_back();
}
}
vector> subsets(vector& nums) {
backtracking(nums,0);
return result;
}
}; 90. 子集 II
集合有重复的元素,需要去重取 横向遍历去重used
解集 不能有重复的,递归i+1
class Solution{
public:
vector> result;
vector path;
void backtracking(vector& nums,int startindex,vector& used){
result.push_back(path);//求子集需要放在终止条件的前面,树中的每一个节点
//可以没有这个
// if(startindex >= nums.size()){
// return;
// }
for(int i = startindex;i < nums.size();i++){
//同一树层去重
if(i>0 && nums[i-1]==nums[i] && used[i-1]==false){
continue;
}
path.push_back(nums[i]);
used[i]=true;
backtracking(nums,i+1,used);
used[i]=false;
path.pop_back();
}
}
vector> subsetsWithDup(vector& nums){
vector used(nums.size(),false);
sort(nums.begin(),nums.end());//去重需要排序
backtracking(nums,0,used);
return result;
}
}; 491. 递增子序列
//使用set去重 本题逻辑上依旧是子集问题,递增子集问题,逻辑上是树的所有节点,但是有终止条件,存放结果集在终止条件的里面,return不要,逻辑上是树的所有节点
class Solution{
public:
vector> result;
vector path;
//一个子集求组合,解集不能重复
void backtracking(vector& nums,int startindex){
//终止条件,子集数量大于两个,就收集
if(path.size() > 1){
result.push_back(path); //不加return的原因,后面还得继续加path
}
unordered_set set;//下次递归都要重新定义为空
//set只用在本树层 去重 (集合有重复元素)
for(int i = startindex;i < nums.size();i++){
//使用set去重
if(!path.empty()&&nums[i] uset; 是记录本层元素是否重复使用,
//新的一层set都会重新定义(清空),所以要知道set只负责本层!
path.push_back(nums[i]);
backtracking(nums,i+1);//解集不能重
path.pop_back();
}
}
vector> findSubsequences(vector& nums){
backtracking(nums,0);
return result;
}
};
//不使用used去重的原因是 要求不对集合排序 优化(数组做哈希记录)
// 版本二
class Solution {
private:
vector> result;
vector path;
void backtracking(vector& nums, int startIndex) {
if (path.size() > 1) {
result.push_back(path);
}
int used[201] = {0}; // 下标从0开始 这里使用数组来进行去重操作,题目说数值范围[-100, 100]
for (int i = startIndex; i < nums.size(); i++) {
if ((!path.empty() && nums[i] < path.back())
|| used[nums[i] + 100] == 1) {
continue;
}
used[nums[i] + 100] = 1; // 记录这个元素在本层用过了,本层后面不能再用了 下标从零开始
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back();
}
}
public:
vector> findSubsequences(vector& nums) {
backtracking(nums, 0);
return result;
}
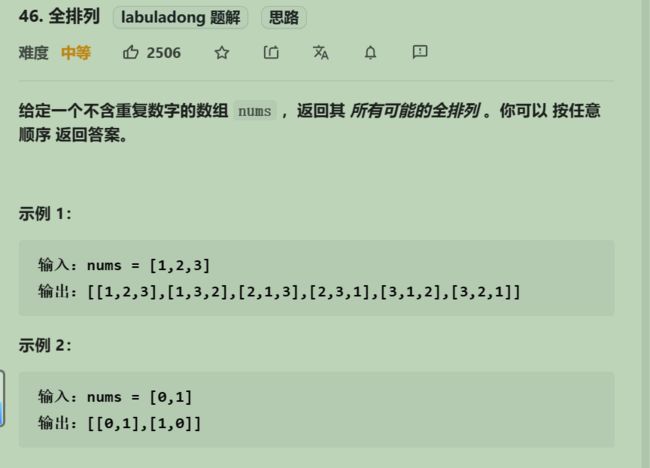
}; 46. 全排列
排列是有序的, [1,2] 和 [2,1] 是两个集合,这和之前分析的子集以及组合所不同的地方。
可以看出元素1在[1,2]中已经使用过了,但是在[2,1]中还要在使用一次1,
所以处理排列问题就不用使用startIndex了。但排列问题需要一个used数组,标记已经选择的元素。
class Solution {
public:
vector> result;
vector path;
void backtracking(vector& nums,vector& used){
if(path.size() == nums.size()){
result.push_back(path);
return;
}
for(int i = 0;i> permute(vector& nums) {
//used 记录本层取了哪些数
//不用index 从0 开始 排列
vector used(nums.size(),false);
backtracking(nums,used);
return result;
}
}; 47. 全排列 II
全排列没有index 递归,但要used ,集合有重复元素,需要横向遍历去重,没有需要used[i] == true,递归判断
//每层都是从0开始搜索而不是startIndex
//需要used数组记录path里都放了哪些元素了 递归
//nums有重复的元素,used去重
//排列也是取叶子节点
class Solution {
public:
vector> result;
vector path;
void backtracking(vector& nums,vector& used){
if(path.size() == nums.size()){
result.push_back(path);
return;
}
for(int i = 0;i0 && nums[i] == nums[i-1] && used[i-1] == false) continue;
//递归下一层已取过
//排列中只能取数组的每一个元素,记录path的存放哪些元素
if(used[i] == true) continue;
path.push_back(nums[i]);
used[i] = true;
backtracking(nums,used);
used[i] = false;
path.pop_back();
}
}
vector> permuteUnique(vector& nums) {
sort(nums.begin(),nums.end());//去重 要 排序 (原数组有重复元素)
vector used(nums.size(),false);
backtracking(nums,used);
return result;
}
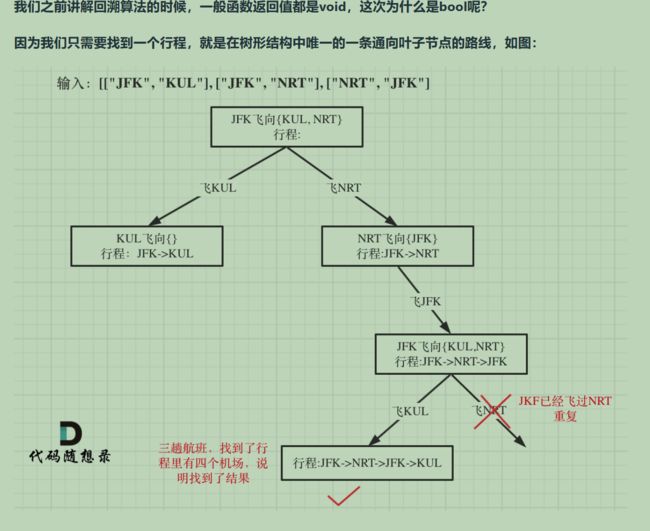
}; 332. 重新安排行程
这道题目有几个难点:
一个行程中,如果航班处理不好容易变成一个圈,成为死循环
有多种解法,字母序靠前排在前面,如何该记录映射关系呢?
使用回溯法(也可以说深搜) 的话,那么终止条件是什么?
搜索的过程中,如何遍历一个机场所对应的所有机场。
class Solution {
public:
//起始机场->到达机场(多个有序) 映射关系++
//unordered_map<出发机场, map<到达机场, 航班次数>> targets
unordered_map> target;
bool backtracking(int ticketsNum,vector& result){
if(result.size() == ticketsNum + 1){
return true;
}
// target[result[尾部元素]==起始机场] 映射为 对应到达机场
for(pair& achive : target[result[result.size()-1]]){
//到达机场航班还没使用
if(achive.second > 0){
result.push_back(achive.first);//加进结果集
achive.second--;//使用了
if(backtracking(ticketsNum,result)) return true;
achive.second++;
result.pop_back();
}
}
return false;
}
vector findItinerary(vector>& tickets) {
vector result;
//初始化
for(const vector& vec: tickets){
target[vec[0]][vec[1]]++; //航班次数统计
}
result.push_back("JFK");
backtracking(tickets.size(),result);
return result;
}
}; 51. N 皇后
class Solution{
public:
vector> result;//结果集是二维数组,里面元素是字符串
void backtracking(int n,int row,vector& N){
//递归的行数到达棋盘底层
if(n == row){
result.push_back(N);
return;
}
//这个for循环遍历已经自动排除不在同一行的情况 每次递归从新一行从头开始
for(int col = 0;col < n;col++){
if(isvalid(row,col,n,N)){
N[row][col] = 'Q';//放皇后
backtracking(n,row+1,N);
N[row][col] = '.';//回溯,撤下皇后
}
}
}
bool isvalid(int row,int col,int n,vector& N){
//皇后不在同一列 i=0&& j >= 0;i--,j--){
if(N[i][j] == 'Q'){
return false;
}
}
//不在斜线45°
for(int i = row - 1,j = col + 1;i>=0&&j < n ;i--,j++){
if(N[i][j] == 'Q'){
return false;
}
}
return true;
}
vector> solveNQueens(int n){
result.clear();
vector N(n,string(n,'.'));//原来是 一维数组,里面元素是字符串
backtracking(n,0,N);
return result;
}
};
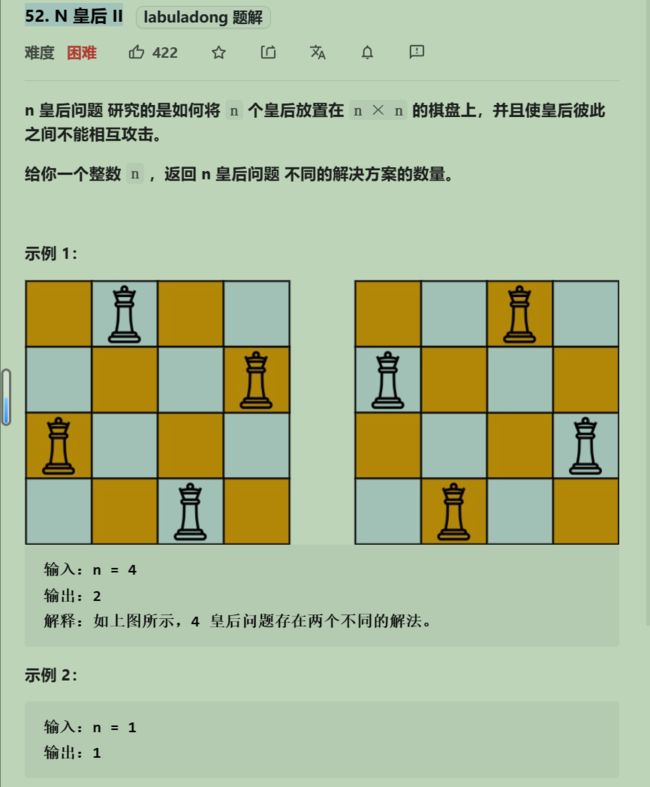
52. N 皇后 II
面试题 08.12. 八皇后
跟N皇后思路一样
class Solution {
private:
vector> result;
// n 为输入的棋盘大小
// row 是当前递归到***的第几行了
void backtracking(int n, int row, vector& chessboard) {
if (row == n) {
result.push_back(chessboard);
return;
}
for (int col = 0; col < n; col++) {
if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
chessboard[row][col] = 'Q'; // 放置皇后
backtracking(n, row + 1, chessboard);
chessboard[row][col] = '.'; // 回溯,撤销皇后
}
}
}
bool isValid(int row, int col, vector& chessboard, int n) {
int count = 0;
// 检查列
for (int i = 0; i < row; i++) { // 这是一个剪枝
if (chessboard[i][col] == 'Q') {
return false;
}
}
// 检查 45度角是否有皇后
for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
// 检查 135度角是否有皇后
for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
return true;
}
public:
vector> solveNQueens(int n) {
result.clear();
std::vector chessboard(n, std::string(n, '.'));
backtracking(n, 0, chessboard);
return result;
}
};
class Solution {
public:
vector> result;
int ans = 0;//直接加一个全局变量
//N 相当于二维... 本质上是一维string 但可以理解成n行n列.
void backtracking(int n , int row, vector& N){
if(row == n){
result.push_back(N);
ans++;
return;
}
for(int col = 0;col < n;col++){
if(isvalid(row,col,n,N)){
N[row][col] = 'Q';
backtracking(n,row+1,N);
N[row][col] = '.';
}
}
}
bool isvalid(int row ,int col,int n,vector& N){
//只判断同一列
for(int i = 0;i=0&&j>=0;i--,j--){
if(N[i][j] == 'Q'){
return false;
}
}
for(int i = row-1,j = col + 1;i>=0&&j N(n,string(n,'.'));
backtracking(n,0,N);
return ans;
}
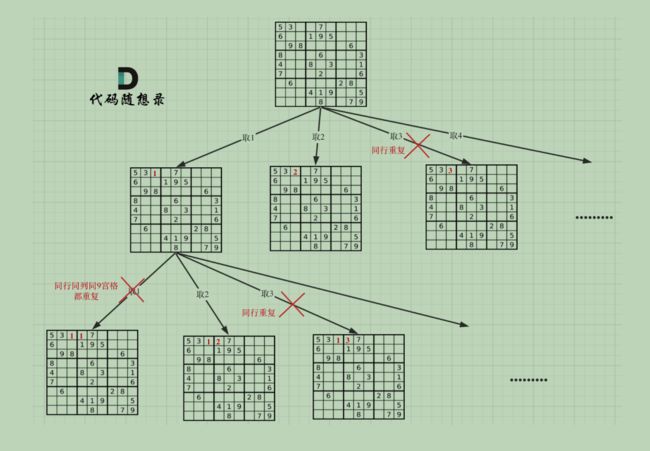
}; 37. 解数独
class Solution{
public:
bool backtracking(vector>& board){
for(int i = 0;i>& board){
//行合法性
for(int i = 0;i < 9;i++){
if(board[row][i] == val) return false;
}
//列合法性
for(int j = 0;j < 9;j++){
if(board[j][col] == val) return false;
}
//小九宫格合法性
int startrow = (row / 3) * 3;
int startcol = (col / 3) * 3;
for(int i = startrow;i < startrow + 3;i++){
for(int j = startcol ;j < startcol + 3;j++){
if(board[i][j] == val) return false;
}
}
return true;//合法
}
void solveSudoku(vector>& board){
backtracking(board);
}
}; Codetop
22. 括号生成
//深度优先遍历 减法(dfs) + 动态规划
class Solution{
public:
void dfs(string cur,int left,int right,vector& result){//结果集一定要带引用!!! 当前字符串可以不用
if( left == 0 && right == 0){
result.push_back(cur);
return ;
}
//当前集合里面 左括号数量 严格大于 右括号数量 用的“))(” 匹配不了此时集合里面左括号大于右括号数量
if(left > right){
return ;
}
if(left > 0){ //用集合里面的一个 左括号(
dfs(cur+"(",left-1,right,result);//cur+"(" cur,本身值没有变 left也是,自动回溯的功能
}
if(right > 0){
dfs(cur+")",left,right-1,result);
}
}
vector generateParenthesis(int n){
vector result;
dfs("",n,n,result); //左括号数量,右括号数量
return result;
}
}; 79. 单词搜索
class Solution {
public:
int da[4][2] = {{-1,0},{0,1},{1,0},{0,-1}};//二维数组4行2列
bool exist(vector>& board, string word) {
int m = board.size();
int n = board[0].size();
vector> res(m,vector(n));//标识是否使用过的二维数组,默认初始化为false
for(int i = 0;i>& board, string& word,vector>& res){
if(wordindex == word.size()-1){
return word[wordindex] == board[x][y];//递归到单词末尾 与原数组位置相同
}
if(word[wordindex] == board[x][y]){//数组当前位置与指定的单词位置匹配
res[x][y] = true;
for(int i = 0;i<4;i++){
int new_x = x + da[i][0];
int new_y = y + da[i][1];//for循环依次向上,向右,下,左走
//下面两个if 都要满足,第一个是四个方向的边界条件以及访问标志数组,一个方向不行for换另外一个方向
if(new_x >= 0 && new_x < board.size() && new_y >= 0 && new_y < board[0].size() && !res[new_x][new_y]){
if(dfs(new_x,new_y,wordindex+1,board,word,res)){//递归的递归,符合条件一直递归下去 wordindex+1有类似于回溯的味道,wordindex 本身没有变,递归加一了而已,递归后不满足条件,依旧是原来的wordindex 值
//满足第二个if,if(true),递归到单词末尾
return true;
}
}
}
res[x][y] = false;//四个方向都没找到满足递归的,当前数组位置虽然匹配一个单词字符,但是递归不下去,回到forfor换新的起始点
}
return false;
}
}; 212. 单词搜索 II(回溯超时+字典树学)
class Solution {
public:
int data[4][2] = {{-1,0},{1,0},{0,1},{0,-1}};
unordered_set s,t; //s 放的是words的单词,t 放的是存在的单词
vector result;
void dfs(int x,int y,string cur,vector>& board,vector& words,vector>& res){
if(cur.size() > 10) return;
if(s.count(cur)) t.insert(cur);
for(auto d : data){
int new_x = x + d[0];
int new_y = y + d[1];
if(new_x >= 0 && new_x < board.size() && new_y >= 0 && new_y < board[0].size() && !res[new_x][new_y]){
res[new_x][new_y] = true;
dfs(new_x,new_y,cur+board[new_x][new_y],board,words,res);
res[new_x][new_y] = false;
}
}
//return;
}
vector findWords(vector>& board, vector& words) {
for(auto str : words) s.insert(str);
int m = board.size();
int n = board[0].size();
string s;//空字符串
vector> res(m,vector(n,false));//标识数组
for(int i = 0;i < m;i++){
for(int j = 0;j < n;j++){
res[i][j] = true;
dfs(i,j,s+board[i][j],board,words,res); //s+board[i][j] 忘加了后面的
res[i][j] = false;
}
}
for(string tt : t) result.push_back(tt);
return result;
}
}; 字典树需要学习
//dfs回溯+tire树剪枝
class Solution {
public:
int son[100010][26]={0},cent[100010]={0},idx=0;
int dp[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}}; //四个移动方向
int n, m;
vector ha;
void insert(string word) { //构建字典树
int p=0;
for(auto i:word){
int u=i-'a';
if(son[p][u]==0) son[p][u]=++idx;
p=son[p][u];
}
cent[p]++;
}
void dfs(vector>& board, int i, int j, string tmp,int id) {
if (i < 0 || j < 0 || i >= n || j >= m) return;
char c = board[i][j];
int u = c - 'a';
//该字符用过则剪枝
if(c == '*' || son[id][u]==0) {
return;
}
id=son[id][u];
//是单词放到ha中,并从字典树剔除
if(cent[id]>=1) {
ha.push_back(tmp+c);
cent[id]= 0;
}
board[i][j] = '*';//标记已经访问过
//上、下、左、右四个方向遍历
for(int k =0; k<4; k++)
dfs(board, i+dp[k][0], j+dp[k][1], tmp + c,id);
board[i][j] = c; //回溯
return;
}
vector findWords(vector>& board, vector& words) {
n = board.size(), m = board[0].size();
for(auto z:words)
insert(z);
for (int i = 0; i < n; i++) //从每个起点开始寻找,是否有满足的单词
for (int j = 0; j < m; j++)
dfs(board, i, j, "",0);
return ha;
}
};
698. 划分为k个相等的子集
相当于是有 k 个一模一样的桶,有nums个球,每个球为nums[i]的大小,问所有球能不能正好装入桶中,桶大小可以调节,但是数目不能变
第一步我们需要将nums个球的总大小求出来,并平均分为k份,确定桶大小
如果平均分成 k 份存在小数,那么肯定会分不均匀,因为我们能用的球,大小只有整数,分不出小数
第二步将球放入桶中,并用递归将所有放入顺序记录下来
第三步,在所有顺序中选择一个可行解即可
其实在上述过程中,我们可以不需要记录所有组合,可以边记录边判断,将当前顺序不可行时,回溯返回上一步
class Solution {
public:
bool divive(vector& nums,int len,int k,int target,int* tmp_arr,int index){
if(index == len){ //枚举完所有元素
for(int i = 0; i < k;i++){ //判断每个桶是否都装满
if(tmp_arr[i] != target) return false;
}
return true;
}
for(int i = 0;i < k;i++){ //枚举每一个桶
if(tmp_arr[i] + nums[index] > target) continue; //当前桶装不下了。换下一个桶 剪枝
tmp_arr[i] += nums[index]; //装了
if(divive(nums,len,k,target,tmp_arr,index+1)) return true; //判断当前桶装了之后,下一个元素是否还能正常装好
tmp_arr[i] -= nums[index]; //下一个不能,说明这个球不是这个桶的,回溯
//如果第一个球,在第一个桶里面装不了,那么因为所有桶都是一样的,
//其他桶肯定也装不了,提前结束
if(tmp_arr[i] == 0) break; //再剪枝 不剪枝通过不了
}
return false;
}
bool canPartitionKSubsets(vector& nums, int k) {
int len = nums.size();
int sum = 0;
for(int i = 0;i < nums.size();i++){
sum += nums[i];
}
if(sum % k != 0) return false;
int target = sum / k;
int tmp_arr[k];
memset(tmp_arr,0,sizeof(int)*k);
return divive(nums,len,k,target,tmp_arr,0);
}
}; 473. 火柴拼正方形
class Solution {
public:
bool makesquare(vector& matchsticks) {
int len = matchsticks.size();
int sum = 0;
for(int i = 0;i < matchsticks.size();i++){
sum += matchsticks[i];
}
if(sum % 4 != 0) return false;
int target = sum / 4; //桶目标
vector tmp_arr(4,0);//4个桶
sort(matchsticks.begin(),matchsticks.end(),greater()); //自大到小排序 !
return dfs(matchsticks,len,tmp_arr,target,0);
}
bool dfs(vector& matchsticks,int len,vector tmp_arr,int target,int index){
if(index == len){ //index遍历下标 到终点
for(int i = 0;i < 4;i++){
if(tmp_arr[i] != target){
return false;
}
return true;
}
}
//遍历四个桶
for(int i = 0;i < 4;i++){
if(tmp_arr[i] + matchsticks[index] > target) continue; //剪枝 不好放当前桶
tmp_arr[i] += matchsticks[index]; //拼
if(dfs(matchsticks,len,tmp_arr,target,index+1)){ //下一个index 递归判断
return true;
}
tmp_arr[i] -= matchsticks[index]; //不拼
if(tmp_arr[i] == 0) break; //当前的拼不了,之后的也拼不了
}
return false;
}
}; 2305. 公平分发饼干
class Solution {
public:
int max_target = INT_MAX; //桶分的最大目标
int distributeCookies(vector& cookies, int k) {
int len = cookies.size();
vector tmp_arr(k,0); //k个桶
sort(cookies.begin(),cookies.end(),greater());//自大到小排序
dfs(cookies,len,k,tmp_arr,0);//不返回
return max_target;
}
void dfs(vector& cookies,int len,int k,vector tmp_arr,int index){
if(index == len){ //下标到终点
max_target = *max_element(tmp_arr.begin(),tmp_arr.end()); //选最大总数
return ;
}
//遍历k个桶
for(int i = 0;i < k;i++){
if(tmp_arr[i] + cookies[index] > max_target || (i > 0 && tmp_arr[i] == tmp_arr[i-1])) continue;
tmp_arr[i] += cookies[index];
dfs(cookies,len,k,tmp_arr,index+1);
tmp_arr[i] -= cookies[index];
}
}
}; 力扣
688. 骑士在棋盘上的概率
//棋盘上的同一个位置在剩余 x 次时有可能会重复的到达,所以,我们需要加一个缓存,这也就是记忆化搜索
class Solution {
public:
const int dir[8][2] ={{2,1},{1,2},{-1,2},{-2,1},{-2,-1},{-1,-2},{1,-2},{2,-1}};
double knightProbability(int n, int k, int row, int column) {
vector>> memo(n,vector>(n,vector(k+1,0)));
return dfs(n,k,row,column,memo);
}
double dfs(int n,int k,int x,int y,vector>>& memo){
if(x < 0 || x >= n || y < 0 || y >= n) return 0;
if(k == 0) return 1;
if(memo[x][y][k] != 0) return memo[x][y][k]; //三个维度
double ans = 0;
for(auto e : dir){
int new_x = x + e[0];
int new_y = y + e[1];
ans += dfs(n,k-1,new_x,new_y,memo)/8.0;
}
memo[x][y][k] = ans; //记录 当前位置的概率
return ans;
}
}; 并查集题型
684. 冗余连接
连接多了有环,删除一条边,不出现环
class Unionfind{
private:
vector parent;
public:
Unionfind(int n){//构造
for(int i = 0;i < n;i++){//n的范围很重要!! [0,1,2,3]
parent.push_back(i);
}
}
//找x的代表节点 路径压缩
int find(int x){
if(x == parent[x]){
return x;
}
parent[x] = find(parent[x]);
return parent[x];
}
//合并两个节点的代表节点
void myunion(int index1,int index2){
parent[find(index1)] = find(index2);
}
};
class Solution {
public:
vector findRedundantConnection(vector>& edges) {
int n = edges.size();//这个很重要!!
Unionfind unionfind(n+1);
for(auto& e : edges){
int index1 = e[0];
int index2 = e[1];
if(unionfind.find(index1) == unionfind.find(index2)){//找到通的,说明有环
//同一个整体集合根节点 有环
return e;
}else{
unionfind.myunion(index1,index2);//不然合并
}
}
return {0,0};
}
}; 547. 省份数量
[1,1,0]第1行第一列 也就是第一号城市和第二号城市没有连通
class Unionfind{
public:
vector parent;
int num ;
Unionfind(int n):num(n){
parent.resize(n);
for(int i =0;i >& isConnected) {
int n = isConnected.size();
Unionfind unionfind(n);
for(int i = 0;i < n;i++){
for(int j = i+1; j < n;j++){
if(isConnected[i][j]){
unionfind.merge(i,j);
}
}
}
return unionfind.get_num();
}
}; 399. 除法求值
//并查集 构建有向图(合并并查集)-> 除法阶段路径压缩
class Solution {
class UnionFind{
private:
vector parent;//父节点
vector weight;//指向父节点的权重值
public:
UnionFind(int n){
for(int i = 0;i < n;i++){
parent.push_back(i);//索引本身的父节点为本身
weight.push_back(1.0);//指向父节点的权重
}
}
//找根节点
int find(int x){
//父节点为索引本身,返回索引本身
//不为索引本身,除法函数用到 路径压缩(当前节点不指向父节点,而是指向根节点)
if(x != parent[x]){
int tmp = parent[x];
parent[x] = find(parent[x]);//递归寻找父节点的根节点
weight[x] *= weight[tmp];//权重值更新为 指向父节点的权重累乘父父节点的权重
}
return parent[x];
}
//构建有向图
void myunion(int x,int y,double value){
int rootx = find(x);//找x 的根节点
int rooty = find(y);
if(rootx == rooty) return;//都指向根节点,直接返回,因为已经构造了
//两个根节点不一样 构建有向图 x的根节点 指向y的根节点,更新权重值
parent[rootx] = rooty;
weight[rootx] = weight[y]*value / weight[x];//weight[y]为y指向父节点的权重,同理x
}
double iscount(int x,int y){
int rootx = find(x);
int rooty = find(y);//找根节点
if(rootx == rooty){
return weight[x.]/weight[y];//此时的权重都是路径压缩后 各自指向根节点的值(非父节点)
}else{
return -1.0;
}
}
};
public:
vector calcEquation(vector>& equations, vector& values, vector>& queries) {
int equationssize = equations.size();
UnionFind unionfind(equationssize*2);//有参构造 初始化并查集
map hashmap; //字符,id 映射
int id = 0;
//存分子 分母 id为其值
for(int i = 0;i equation = equations[i];//一维数组
string var1 = equation[0];
string var2 = equation[1];
if(!hashmap.count(var1)){
hashmap[var1] = id;
id++;
}
if(!hashmap.count(var2)){
hashmap[var2] = id;
id++;
}
unionfind.myunion(hashmap[var1],hashmap[var2],values[i]);//构建有向图 合并
}
//查询 求得两个分子分母变量是否在集合里 做除法
int queriessize = queries.size();
vector res(queriessize,-1.0);
for(int i = 0;i < queriessize;i++){
string var1 = queries[i][0];
string var2 = queries[i][1];
int id1 ,id2;
if(hashmap.count(var1) && hashmap.count(var2)){//查询变量是否在集合里(哈希表装着已有变量)
id1 = hashmap[var1];
id2 = hashmap[var2];
res[i] = unionfind.iscount(id1,id2);
}
}
return res;
}
}; 贪心算法题型
代码随想录
贪心的本质是选择每一阶段的局部最优,从而达到全局最优
例如,有一堆钞票,你可以拿走十张,如果想达到最大的金额,每回拿最大的,最终结果就是拿走最大数额的钱。
每次拿最大的就是局部最优,最后拿走最大数额的钱就是推出全局最优。
刚刚举的拿钞票的例子,就是模拟一下每次拿做大的,最后就能拿到最多的钱,不需要数学推理
贪心算法一般分为如下四步:
将问题分解为若干个子问题
找出适合的贪心策略
求解每一个子问题的最优解
将局部最优解堆叠成全局最优解
455. 分发饼干
局部最优:每次比较 大饼干喂给胃口大的,充分利用饼干尺寸喂饱一个,全局最优:喂饱尽可能多的小孩
//每一次喂孩子,拿最大的饼干喂最大胃口的孩子(局部最优),从而满足更多孩子(整体最优)
class Solution{
public:
int findContentChildren(vector& g,vector& s){
sort(g.begin(),g.end());
sort(s.begin(),s.end());
int result = 0;//孩子数量记录
int index = s.size() - 1;//两层for循环变成一个for,遍历饼干数组下标自减,从后往前遍历
for(int i = g.size()-1;i >= 0;i--){
//满足孩子一次,处理结果一次
if(index >= 0 && s[index] >= g[i]){
result++;
index--;//两层for循环变成一个for,遍历饼干数组下标自减
}
}
return result;
}
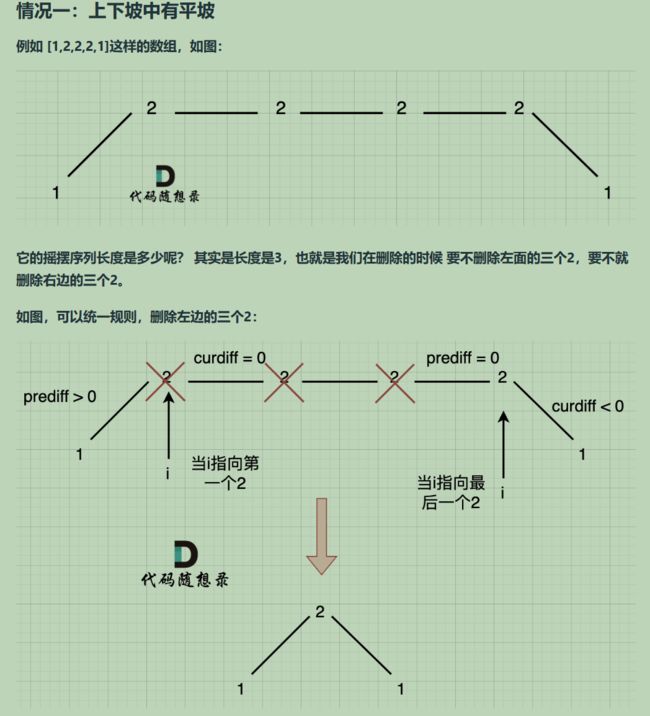
}; 376. 摆动序列
子序列:非连续的序列
//局部最优:单调坡度删掉中间的几个节点,留两端峰值点,当前的最大子序列长度
//全局最优:更多的峰值点
//局部最优:每次删掉单调坡度中间几个节点(不包括单调坡度两端的节点),保证坡度有两个峰值
//整体最优:统计尽可能多的峰值,求出最长子序列的长度
//特殊情况:[1,3] 有两个峰值,按统计差值来求只有一个峰值,需要设置前,当前差值 统计 峰值个数
class Solution{
public:
int wiggleMaxLength(vector& nums){
if(nums.size() <= 1) return nums.size();
int curdiff = 0;
int prediff = 0;
int result = 1; //记录峰值个数,序列默认序列最右边有一个峰值
for(int i = 0;i < nums.size() -1 ;i++){//i < nums.size() -1
curdiff = nums[i+1] - nums[i];
//出现峰值
if( prediff<=0 && curdiff > 0 || prediff>= 0&& curdiff < 0){
result++;
prediff = curdiff;// 注意这里,只在摆动变化的时候更新prediff
}
}
return result;
}
}; 53. 最大子数组和
局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。(是连续和为负数时,才放弃,不是遇到负数)
全局最优:选取最大“连续和”
优势:不断调整最大子序和区间的起始位置,记录各阶段的最大值
class Solution {
public:
int maxSubArray(vector& nums) {
int result = INT_MIN;
int cur = 0;
for(int i = 0;i < nums.size();i++){ //局部最优:每一次i当前遍历的情况取最优,连续和不为负数
cur += nums[i];
if(cur > result) result = cur; //取区间累计的最大值(相当于不断确定最大子序终止位置)
if(cur < 0) cur = 0; //相当于重置最大子序起始位置,因为遇到负数一定是拉低总和
}
return result;
}
};
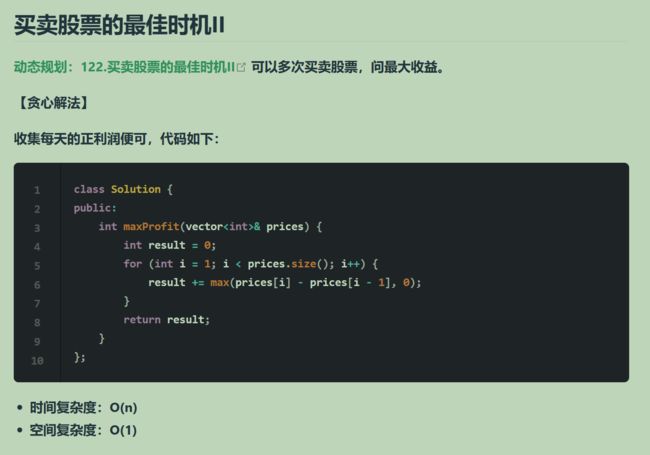
122. 买卖股票的最佳时机 II
局部最优:收集每天i的正利润,全局最优:求得最大利润。
关键点:利润拆分
class Solution {
public:
int maxProfit(vector& prices) {
int result = 0;
for(int i = 1;i < prices.size();i++){
result += max(prices[i]-prices[i-1],0); //每天只收集利润正的
}
return result;
}
}; 55. 跳跃游戏
局部最优:每次i取最大跳跃步数(取最大覆盖范围),不管跳几步,因为i会一个个遍历
整体最优解:最后得到整体最大覆盖范围,看是否能到终点(i到最后下标时)
class Solution {
public:
bool canJump(vector& nums) {
int skip = 0;
if(nums.size()==1) return true;
//当前位置 只到 skip的最大位置,i一步步遍历
//关键i<=skip 关键:每一步i ,当前能跳的范围
for(int i = 0;i<=skip;i++){ //i<=skip 非i <= nums.size()
//i位置再跳nums[i]步 更新可跳的最大边界值
skip = max(skip,i+nums[i]);//关键
if(skip >= nums.size()-1) return true;
}
return false;
}
}; 45. 跳跃游戏 II
计算最小步数,想清楚什么时候步数才一定要加一?
局部最优:当前可移动距离尽可能多走,如果还没到终点,步数再加一。
整体最优:一步尽可能多走,从而达到最小步数。
需要统计两个覆盖范围,当前这一步的最大覆盖和下一步最大覆盖
如果遍历下标达到了当前这一步的最大覆盖最远距离下标了,还没有到终点的话,那么就必须再走一步来增加覆盖范围,直到覆盖范围覆盖了终点。
class Solution {
public:
int jump(vector& nums) {
if(nums.size() <= 1) return 0;
int curdistance = 0;
int nextdistance = 0;
int result = 0;//步数
for(int i = 0;i& nums) {
if(nums.size() <= 1) return 0;
int cur_max = 0; //当前最远覆盖
int next_max = 0;//下一个最远覆盖
int skip = 0; //跳的次数
for(int i = 0;i < nums.size();i++){
next_max = max(next_max,i+nums[i]); //每一步的最远覆盖
if(i == cur_max){ //下标到当前最远覆盖
if(i != nums.size()-1){ //还没到终点
skip++; //跳一次
cur_max = next_max;//更新当前最远覆盖
}else{
break; //到终点
}
}
}
return skip;
}
}; 1005. K 次取反后最大化的数组和
局部最优:遍历到的i能让绝对值大的负数变为正数,当前数值达到最大 (绝对值大的负数的对应下标i,不是每次i)
整体最优:整个数组和达到最大。
第一步:将数组按照绝对值大小从大到小排序,注意要按照绝对值的大小
第二步:从前向后遍历,遇到负数将其变为正数,同时K--
第三步:如果K还大于0,那么反复转变数值最小的元素,将K用完
第四步:求和
class Solution {
public:
static bool cmp(int a , int b){
return abs(a) > abs(b);
}
int largestSumAfterKNegations(vector& nums, int k) {
//绝对值 自大到小 排序
//取反挑最大负数,最后k为奇数,取反排序后的最小值
sort(nums.begin(),nums.end(),cmp);
int result = 0;
for(int i = 0;i 0){
nums[i] *= (-1);
k--;
}
}
//奇数 最后位置取反
//取反挑最大负数,最后k为奇数,取反排序后的最小值
if(k%2 == 1){
nums[nums.size()-1] *= (-1);
}
for(int i : nums){
result += i;
}
return result;
}
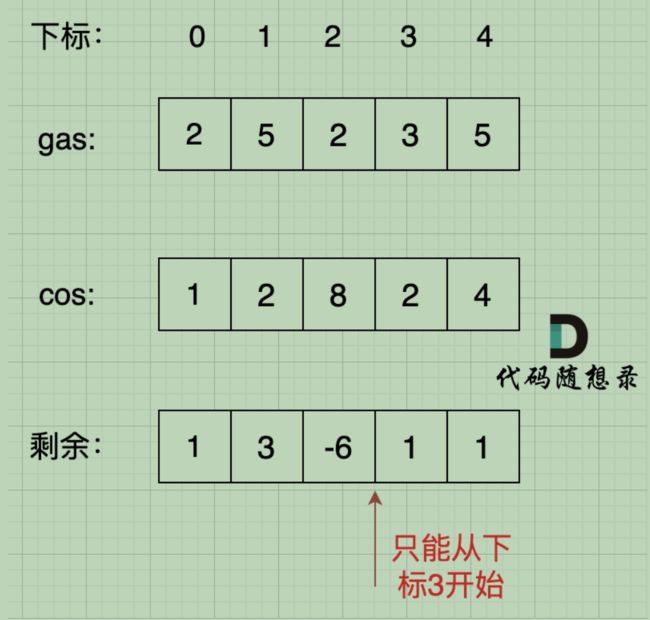
}; 134. 加油站
解法一:直接从全局进行贪心选择,情况如下:
情况一:如果gas的总和小于cost总和,那么无论从哪里出发,一定是跑不了一圈的
情况二:rest[i] = gas[i]-cost[i]为一天剩下的油,i从0开始计算累加到最后一站,如果累加没有出现负数,说明从0出发,油就没有断过,那么0就是起点。
情况三:如果累加的最小值是负数,汽车就要从非0节点出发,从后向前,看哪个节点能把这个负数填平,能把这个负数填平的节点就是出发节点。
class Solution{
public:
int canCompleteCircuit(vector& gas,vector& cost){
int min = INT_MAX;//遍历完全部:剩余油量累加和的最小值 为负数,说明不能从0开始跑
int rest = 0;
int curSum = 0;
for(int i = 0;i < cost.size();i++){
rest = gas[i] - cost[i];
curSum += rest;
if(curSum < min){
min = curSum; //剩余油量累加和 出现的 最小值
}
}
if(curSum < 0) return -1;//总汽油量-总消耗量 小于零,不存在 环
if(min >= 0){
return 0;//遍历完全部:剩余油量累加和的最小值 不为负数,可以从0开始跑
}else {//min小于零,不在下标0,从后往前抵消负数,就是开始位置
for(int i = cost.size()-1;i>= 0;i--){
int rest = gas[i] - cost[i];
min += rest;
if(min >= 0){
return i;
}
}
}
return -1;
}
}; 解法二:
每个加油站的剩余量rest[i]为gas[i] - cost[i]。
i从0开始累加rest[i],和记为curSum,一旦curSum小于零,说明[0, i]区间都不能作为起始位置,因为这个区间选择任何一个位置作为起点,到i这里都会断油,那么起始位置从i+1算起,再从0计算curSum。
局部最优:当前i累加剩余油量的和 小于零,从下一个位置i+1为起始位置,因为i开始完不成环
全局最优: 找到环绕一周的起始位置下标
class Solution{
public:
int canCompleteCircuit(vector& gas,vector& cost){
int start = 0;//记录起始位置
int curSum = 0;//当前剩余油量
int totalSum = 0;//总汽油-总消耗量大于零,一定存在环绕一周的起始位置
for(int i = 0;i < cost.size();i++){
curSum += gas[i]-cost[i];//当前剩余油量累加(动态累加,小于零从0开始,下一个起始点,局部最优 贪心所在
totalSum += gas[i] - cost[i];//一直累加
if(curSum < 0){
start = i + 1;
curSum = 0;
}
}
if(totalSum < 0) return -1;
return start;
}
}; 135. 分发糖果
分开考虑,先从左到右,再从右到左
从左往右 i从1开始与前面的比较(第一,第二) 从右往左 i从倒数第二位开始比较(倒数第一,倒数第二)
1、从前向后遍历
此时局部最优:只要右边评分比左边大,右边的孩子就多一个糖果,全局最优:相邻的孩子中,评分高的右孩子获得比左边孩子更多的糖果
2、从后向前遍历 (再确定左孩子大于右孩子的情况)
此时局部最优:取candyVec[i + 1] + 1 和 candyVec[i](从前向后遍历的) 最大的糖果数量,保证第i个小孩的糖果数量既大于左边的也大于右边的。
全局最优:相邻的孩子中,评分高的孩子获得更多的糖果
如果 ratings[i] > ratings[i + 1],此时candyVec[i](第i个小孩的糖果数量)就有两个选择了,一个是candyVec[i + 1] + 1(从右边这个加1得到的糖果数量),一个是candyVec[i](之前比较右孩子大于左孩子得到的糖果数量)。保证相邻点,多于左边也多于右边
//当前节点 比相邻左右孩子节点 考虑 要多
//当前右节点 顺序
//当前左节点 逆序
//从左往右 i从1开始与前面的比较(第一,第二) 从右往左 i从倒数第二位开始比较(倒数第一,倒数第二)
class Solution {
public:
int candy(vector& ratings) {
vector candy(ratings.size(),1);
for(int i = 1;i ratings[i-1]){
candy[i] = candy[i-1]+1;//当前右节点 比左节点多一个糖果
}
}
for(int i = ratings.size()-2;i>=0;i--){
if(ratings[i] > ratings[i+1]){
candy[i] = max(candy[i],candy[i+1]+1);//利用上一个节点 ,当前左节点比右节点多一个糖果
}
}
int result = 0;
for(int i : candy){
result += i;
}
return result;
}
}; 406. 根据身高重建队列
局部最优:优先按身高高的people的k来插入。插入操作过后的people满足队列属性
全局最优:最后都做完插入操作,整个队列满足题目队列属性
// 分发糖果类似,两个维度,先将身高(先确定身高维度)从大到小的排列(相同身高 按人数k(第二维度)从小到大排列)
// 再进行插入操作 局部最优:优先按身高高的一维数组的k值插入对应位置
// 排序:[身高降序,人数升序] 插入:按人数
class Solution{
public:
static bool cmp(vector& a,vector& b){
if(a[0] == b[0]) return a[1] < b[1];//身高h相同,人数k从小到大排
return a[0] > b[0];
}
vector> reconstructQueue(vector>& people){
sort(people.begin(),people.end(),cmp);
vector> result;
//贪心所在
for(int i = 0;i < people.size();i++){
int position = people[i][1];
//提取二维数组的一维数组的第二个元素,按照k直接插入语操作
result.insert(result.begin()+position,people[i]);
//提取二维数组的一维数组插指定位置插入 vector 的insert插入操作的时间复杂度为 o(n^2)
}
return result;
}
};
// //插入操作优先选 list容器
// class Solution {
// public:
// // 身高从大到小排(身高相同k小的站前面)
// static bool cmp(const vector& a, const vector& b) {
// if (a[0] == b[0]) return a[1] < b[1];
// return a[0] > b[0];
// }
// vector> reconstructQueue(vector>& people) {
// sort (people.begin(), people.end(), cmp);
// list> que; // list底层是链表实现,插入效率比vector高的多
// for (int i = 0; i < people.size(); i++) {
// int position = people[i][1]; // 插入到下标为position的位置
// list>::iterator it = que.begin();//链表用迭代器从起始位置开始,while递减
// while(position--){
// it++;
// }
// que.insert(it,people[i]);
// }
// return vector>(que.begin(), que.end());//链表转化为vector数组
// }
// }; 860. 柠檬水找零
class Solution {
public:
bool lemonadeChange(vector& bills) {
int five = 0,ten = 0,twenty = 0;
for(auto bill : bills){
if(bill == 5){
five++;
}
if(bill == 10){
if(five>0){
five--;
ten++;
}else{
return false;
}
}
if(bill == 20){
if(five>0&&ten>0){
five--;
ten--;
twenty++;
}else if(five > 2){
five -= 3;
twenty++;
}else{
return false;
}
}
}
return true;
}
};
452. 用最少数量的箭引爆气球
局部最优:当气球出现重叠,一起射,所用弓箭最少,找x值相同。
全局最优:把所有气球射爆所用弓箭最少。
先左边界排序(第i区间)
当前i 重叠 更新最右小边界,非重叠 预定加一箭
class Solution {
public:
static bool cmp(vector& a,vector& b){
return a[0] < b[0];
}
int findMinArrowShots(vector>& points) {
if(points.size() == 0) return 0;
int result = 1;//非空,预处理,必有一箭
//按左边界排序
sort(points.begin(),points.end(),cmp);
for(int i = 1;ipoints[i-1][1]){
result++;
//重叠区间 更新当前最小有界
}else if(points[i][0] <= points[i-1][1]){
points[i][1] = min(points[i-1][1],points[i][1]);
}
}
return result;
}
};
435. 无重叠区间
//先算非重叠区间个数,再反算重叠区间个数==移除区间个数
class Solution {
public:
static bool cmp(vector& a,vector& b){
return a[1] < b[1];
}
int eraseOverlapIntervals(vector>& intervals) {
if(intervals.size() == 0) return 0;
sort(intervals.begin(),intervals.end(),cmp);
int end = intervals[0][1];//非重叠区间位置
int count = 1; //非重叠区间个数
for(int i = 1;i < intervals.size();i++){
if(intervals[i][0] >= end){
count++;
end = intervals[i][1];//下一个非重叠区间位置
}
}
return intervals.size() - count; //重叠区间个数==移除区间个数
}
}; class Solution {
public:
static bool cmp(vector& a,vector& b){
return a[0] < b[0];
}
int eraseOverlapIntervals(vector>& intervals) {
if(intervals.size() == 0) return 0;
int result = 1; //非重叠区间个数
//左边界排序
sort(intervals.begin(),intervals.end(),cmp);
for(int i = 1;i= intervals[i-1][1]){
result++;//非重叠区间个数
}else if(intervals[i][0] < intervals[i-1][1]){ //重叠区间
intervals[i][1] = min(intervals[i][1],intervals[i-1][1]);
}
}
return intervals.size() - result; // 重叠区间个数 == 需要移除重叠区间的最小数量
}
}; 763. 划分字母区间
统计每一个字符最后出现的位置
从头遍历字符,并更新字符的最远出现下标,如果找到字符最远出现位置下标和当前下标相等了,则找到了分割点
class Solution {
public:
vector partitionLabels(string s) {
vector result;
if(s.size() == 0) return result;
//数组哈希
int nums[27] = {0};
//每个字符 的最远下标位置记录
for(int i = 0;i 56. 合并区间
判断区间重叠
class Solution {
public:
static bool cmp(vector& a,vector& b){
return a[0] < b[0];
}
vector> merge(vector>& intervals) {
vector> result;
if(intervals.size() == 0 ) return result;
//左边界升序排序
sort(intervals.begin(),intervals.end(),cmp);
bool final = false;//标识最后区间合并与否
for(int i = 1;i= intervals[i][0]){
end = max(intervals[i][1],end);//重叠的更新右边界
if(i == intervals.size()-1) final = true;//成功合并最后区间 i++;//继续合并
}
result.push_back({start,end});
}
//处理未标识的 最后区间
//while(i++)导致i提前到末尾下标,最后区间没有合并需要单独处理
//i没合并最后区间,需要单独处理 加进去
if(final == false){
result.push_back({intervals[intervals.size()-1][0],intervals[intervals.size()-1][1]});
}
return result;
}
}; 738. 单调递增的数字
class Solution {
public:
int monotoneIncreasingDigits(int n) {
// 32 -> 29
string s = to_string(n);
int start_9 = s.size(); //1234 不改
for(int i = s.size()-1;i > 0;i--){
if(s[i-1] > s[i]){
s[i-1]--;//上一个值减一 满足小于等于后面
start_9 = i;//更新9开始的位置
}
}
//依次处理 str[i-1]--
for(int i = start_9;i < s.size();i++){
s[i] = '9';
}
return stoi(s);
}
};968. 监控二叉树
局部贪心 用最少的摄像头将所有的节点 都覆盖 (重点是所有节点 都覆盖),最好的就是叶子节点的父节点放一个摄像头,上中下都覆盖,如果放在叶子节点,少一层覆盖
class Solution {
public:
int result;//摄像头数量
//0 无覆盖状态
//1 有摄像头状态
//2 有覆盖状态
int traversla(TreeNode* cur){
if(cur==NULL) return 2;
//空节点为有覆盖状态(自己设定的) 摄像头放在叶子节点的父节点,叶子节点为覆盖状态,空节点只能自己设有覆盖状态
//后序遍历
int left = traversla(cur->left);
int right = traversla(cur->right);
if(left==2 && right == 2) return 0;//只要左右孩子有覆盖,当前根节点不做操作无覆盖状态
//无覆盖的代码放在前面
if(left == 0 || right == 0){
result++; //当前节点需要摄像头,覆盖孩子
return 1;
}
if(left == 1 || right == 1) return 2; //最后左或右孩子有摄像头状态,当前为有覆盖状态
return -1;
}
int minCameraCover(TreeNode* root) {
if(traversla(root) == 0){
result++;
}
return result;
}
};栈和队列题型
代码随想录
栈与队列理论基础
C++中stack 是容器么?
我们使用的stack是属于哪个版本的STL?
我们使用的STL中stack是如何实现的?
stack 提供迭代器来遍历stack空间么?
三个最为普遍的STL版本:
HP STL 其他版本的C++ STL,一般是以HP STL为蓝本实现出来的,HP STL是C++ STL的第一个实现版本,而且开放源代码。
P.J.Plauger STL 由P.J.Plauger参照HP STL实现出来的,被Visual C++编译器所采用,不是开源的。
SGI STL 由Silicon Graphics Computer Systems公司参照HP STL实现,被Linux的C++编译器GCC所采用,SGI STL是开源软件,源码可读性甚高。
栈提供push 和 pop 等等接口,所有元素必须符合先进后出规则,所以栈不提供走访功能,也不提供迭代器(iterator)。 不像是set 或者map 提供迭代器iterator来遍历所有元素
栈是以底层容器(vector,deque,list 数组或者链表的底层实现)完成其所有的工作,对外提供统一的接口,底层容器是可插拔的(也就是说我们可以控制使用哪种容器来实现栈的功能),
所以STL中栈、队列往往不为容器,而被归类为container adapter(容器适配器)
SGI STL,如果没有指定底层实现的话,默认是以deque为缺省情况下栈的底层结构
deque是一个双向队列,只要封住一段,只开通另一端就可以实现栈的逻辑了。
SGI STL中 队列底层实现缺省情况下一样使用deque实现的。
std::stack > third; // 使用vector为底层容器的栈 队列中先进先出的数据结构,同样不允许有遍历行为,不提供迭代器, SGI STL中队列一样是以deque为缺省情况下的底部结构。
std::queue> third; // 定义以list为底层容器的队列 20. 有效的括号
class Solution {
public:
bool isValid(string s) {
if(s.size() % 2 == 1) return false;
stack st;
for(int i = 0;i < s.size();i++){
if(s[i] == '('){
st.push(')');
}else if(s[i] == '{'){
st.push('}');
}else if(s[i] == '['){
st.push(']');
}else if(st.empty() || s[i] != st.top() ) { //不匹配
return false;
}else{
st.pop();
}
}
return st.empty(); //最终判断是否为空
}
}; 1047. 删除字符串中的所有相邻重复项
class Solution{
public:
string removeDuplicates(string S){
stack st;//用栈 做 "消消乐"
for(char s : S){
if(st.empty() || s != st.top()){ //若栈为空加元素或者 栈顶元素与待加元素不一致
st.push(s);
}
else {
st.pop(); //栈顶元素与待加元素一致,退栈顶元素
}
}
string result = ""; //定义新字符串
while(!st.empty()){
result += st.top(); //累加栈元素
st.pop(); //退栈
}
reverse(result.begin(),result.end()); //栈累加的是倒序,反转
return result;
}
}; 150. 逆波兰表达式求值
//逆波兰表达式是后缀表达式
class Solution{
public:
int evalRPN(vector& tokens){
stack st; //栈里面的元素为整数,不是字符串
for(int i = 0;i < tokens.size(); i++){
if(tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/"){ //没遇到符号不用放进栈中,数值才放
int nums1 = st.top(); //记录栈顶元素两次,再退栈
st.pop();
int nums2 = st.top();
st.pop();
if(tokens[i] == "+") st.push(nums2+nums1);//两两相加抵消再放进栈
if(tokens[i] == "-") st.push(nums2-nums1);//nums2放前面,nums2先进后退
if(tokens[i] == "*") st.push(nums2*nums1);
if(tokens[i] == "/") st.push(nums2/nums1);
}
else st.push(stoi(tokens[i])); //将字符串转为数字
}
int result = st.top(); //记录最终栈顶的元素
st.pop();
return result;
}
}; 239. 滑动窗口最大值
思考 为什么不用优先级队列 ?而是用单调队列, 优先级队列无法删除数值,而且都是按顺序排的,不维护窗口的数值
窗口是移动的,而大顶堆每次只能弹出最大值,我们无法移除其他数值,这样就造成大顶堆维护的不是滑动窗口里面的数值了。所以不能用大顶堆。
//deque 加减元素,pop_back(),push_back() 指明位置
class Solution{
public:
class Myqueue{
public:
deque que;//定义仅在对头添加删除的 deque队列
void pop(int value){
if(!que.empty() && value == que.front()){//旧滑动窗口的对头元素的最大值 非||
que.pop_front();//que.pop()不明确,这是deque容器
}
}
void push(int value){
while(!que.empty() && value > que.back()){
que.pop_back(); //value值大于队尾
}
que.push_back(value);//往队尾加,
}
int front(){
return que.front(); //易错
}
};
vector maxSlidingWindow(vector& nums,int k){
Myqueue que;//定义单调队列的类对象
vector result;//定义结果集
for(int i = 0;i < k;i++){ //第一次滑动窗口k=3;建立单调递减的队列,只维护可能的最大值,添加看类函数设计
que.push(nums[i]);
}
result.push_back(que.front()); //记录第一次滑动窗口的最大值 队头元素
for(int i=k;i 347. 前 K 个高频元素
class Solution {
public:
class cmp{
public:
bool operator()(pair& a,pair& b){
return a.second > b.second;
}
};
vector topKFrequent(vector& nums, int k) {
unordered_map map; //[值,出现次数]
for(int i = 0;i < nums.size();i++){
map[nums[i]]++;
}
priority_queue,vector>,cmp> que; //构建小顶堆队列
for(unordered_map :: iterator it = map.begin();it != map.end();it++){
que.push(*it);
if(que.size() > k){ //前k个 入堆
que.pop();
}
}
vector result;
for(int i = 0;i < k;i++){
result.push_back(que.top().first);
que.pop();
}
reverse(result.begin(),result.end());
return result;
}
}; 215. 数组中的第K个最大元素
解法一小根堆优先队列
时间复杂度o(nlogk),遍历数据 O(N),堆内元素调整 O(logK)
空间复杂度:O(K)
class Solution {
public:
int findKthLargest(vector& nums, int k) {
priority_queue,greater> pri_que;
// priority_queue<数据类型,容器,比较器> 构建小顶堆
//priority_queue,less > big_heap2; 构建大顶堆
for(int i = 0;i topmax){
pri_que.pop();//先退出顶部元素,再放入更大值
pri_que.push(nums[i]);
}
}
return pri_que.top();//顶堆顶部为第k个元素
}
}; o(n)解法 --快排
//快排 分而治之 左边为比目标小的数,右边为比目标大的数
class Solution {
public:
int sort(int left,int right,vector& nums){//快排中一趟划分
int tmp = nums[left];//将当前表中第一个元素设为枢纽,对表进行划分
while(left < right){
if(left < right && nums[right] >= tmp) right--;
nums[left] = nums[right];//将比枢纽小的元素移动到左端
if(left < right && nums[left] <= tmp) left++;//将比枢纽大的元素移动到右端
nums[right] = nums[left];
}
nums[left] = tmp;//枢纽元素存放到最终位置
return left;//返回枢纽元素的最终位置
}
int quickSort(int left ,int right,vector& nums,int k){
//二分
int mid = sort(left,right,nums);
if(mid == nums.size()-k){ //第k大
return nums[mid];
}else if(mid < nums.size()-k){ //右边找
return quickSort(mid+1,right,nums,k); //第K大元素在mid右边,则对mid右边继续划分,找出第K大元素
}else{
return quickSort(left,mid-1,nums,k);//第K大元素在mid左边,则对mid左边继续划分,找出第K大元素
}
}
int findKthLargest(vector& nums, int k) {
return quickSort(0,nums.size()-1,nums,k);
}
};
//weiwei解析的双快排性能更好 双指针题型
代码随想录
27. 移除元素
class Solution {
public:
int removeElement(vector& nums, int val) {
int leftIndex = 0;
int rightIndex = nums.size() - 1;
while (leftIndex <= rightIndex) {
//left 遍历到为 val的 val为删除值
while (leftIndex <= rightIndex && nums[leftIndex] != val){
++leftIndex;
}
//right 遍历到不为 val的
while (leftIndex <= rightIndex && nums[rightIndex] == val) {
-- rightIndex;
}
// 将右边不等于val的元素覆盖左边等于val的元素
if (leftIndex < rightIndex) {
nums[leftIndex++] = nums[rightIndex--];
}
}
return leftIndex; // leftIndex一定指向了最终数组末尾的下一个元素
}
}; 344. 反转字符串
//双指针
class Solution{
public:
void reverseString(vector& s){
for(int i=0,j=s.size()-1;i 剑指 Offer 05. 替换空格
//双指针(字符串结合数组) 新旧末尾双指针
class Solution{
public:
string replaceSpace(string& s){
int count =0;//统计空格的大小
int sOldsize = s.size();
for(int i = 0;i151. 反转字符串中的单词
//1、删空格(双指针)
//2、反转字符串思路(整个字符串)
//3、反转局部单词 字符串
class Solution{
public:
void reverse(string& s,int start , int end){
for(int i=start,j=end;i206. 反转链表
//递归
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(head == nullptr || head->next == nullptr) return head;
ListNode* tmp = reverseList(head->next);//tmp认为反转后的节点
head->next->next = head;//在头节点更改顺序
head->next = nullptr;
return tmp;
}
};24. 两两交换链表中的节点
//递归
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
if (head == nullptr || head->next == nullptr) {
return head;
}
ListNode* newHead = head->next;
head->next = swapPairs(newHead->next);
newHead->next = head;
return newHead;
}
};面试题 02.07. 链表相交
//定义两个当前节点,遍历出各自长度,设A为大长度,求出长度差,while找到大长度的当前节点curA与curB一起遍历指针是否相等,若指针相等就找到了交点
class Solution{
public:
ListNode* getIntersectionNode(ListNode* headA,ListNode* headB){
ListNode* curA = headA;
ListNode* curB = headB;
int lenA = 0,lenB = 0;
while(curA != NULL){
lenA++;
curA=curA->next;
}
while(curB != NULL){
lenB++;
curB = curB->next;
}
curA = headA;
curB = headB;
if(lenB > lenA){// 让curA为最长链表的头,lenA为其长度
swap(lenA,lenB);
swap(curA,curB);
}
int gap = lenA - lenB;
while(gap--){// 让curA和curB在同一起点上(末尾位置对齐)
curA=curA->next;
}
while(curA!=NULL){
if(curA==curB){
return curA; // 遍历curA 和 curB,遇到相同则直接返回
}
else{
curA = curA -> next;
curB = curB ->next;
}
}
return curA;
}
};142. 环形链表 II
// 判断链表是否环 , 用双指针 快慢指针, 找到相遇节点 快指针走两个节点,慢指针走一个节点,若有环一定相遇,慢指针在快指针的前一个节点,两指针同时走一步便相遇
// 如果有环,如何找到这个环的入口 ,再定义两个指针 一个头节点,一个相遇节点,两指针再相遇就是环入口节点,通过数学推理
class Solution{
public:
ListNode* detectCycle(ListNode* head){
ListNode* fast = head;
ListNode* slow =head;
while(fast!=NULL && fast->next!=NULL){//环至少需要两个节点
slow = slow->next;
fast = fast->next->next;
if(slow==fast){//快慢指针找到相遇节点,找环的入口
ListNode* index1=head;
ListNode* index2 = fast;
while(index1!=index2){//在定义两个指针,再相遇便是环的节点
index1 = index1->next;
index2 = index2->next;
}
return index2;//找到入口环的节点
}
}
return NULL;
}
};15. 三数之和
去重逻辑 + 双指针
class Solution {
public:
vector> threeSum(vector& nums) {
vector> result;
sort(nums.begin(),nums.end());
for(int i = 0;i < nums.size();i++){
if(nums[i] > 0) return result;
//还要考虑i 去重逻辑
if(i > 0 && nums[i] == nums[i-1]) continue;
int l = i+1,r = nums.size()-1;
while(l < r){
if(nums[i] + nums[l] + nums[r] > 0) r--;
else if(nums[i] + nums[l] + nums[r] < 0) l++;
else{
result.push_back({nums[i],nums[l],nums[r]});
//去重逻辑放在 找到三元组的后面
while(l < r && nums[r] == nums[r-1]) r--;
while(l < r && nums[l] == nums[l+1]) l++;
l++;
r--;
}
}
}
return result;
}
}; 18. 四数之和
class Solution{
public:
vector> fourSum(vector& nums,int target){
vector> result;
sort(nums.begin(),nums.end());
for(int k =0;ktarget&&nums[k]>=0&&target>=0) break;
// 这里使用break停止for循环,统一通过最后的return返回
// 对nums[k]去重
if(k>0&&nums[k]==nums[k-1]){
continue;
}
for(int i = k+1;itarget&&nums[i]+nums[k]>=0&&target>=0) break;
// 对nums[i]去重
if(i>k+1&&nums[i]==nums[i-1]){
continue;
}
int left = i+1;
int right = nums.size()-1;
while(left target 会溢出 加(long)
if((long)nums[i]+nums[k]+nums[left]+nums[right] > target) right--;
else if((long)nums[i]+nums[k]+nums[left]+nums[right] < target) left++;
else{
result.push_back(vector{nums[k],nums[i],nums[left],nums[right]});
// 对nums[left]和nums[right]去重
while(right>left&&nums[right]==nums[right-1]) right--;
while(right>left&&nums[left]==nums[left+1]) left++;
// 找到答案时,双指针同时收缩
left++;
right--;
}
}
}
}
return result;
}
}; 977. 有序数组的平方
//双指针 两边凑近
class Solution{
public:
vector sortedSquares(vector& A){
int k = A.size()-1;
vector result(A.size(),0);
for(int i = 0 , j = A.size()-1 ; i<=j ;){
if(A[i]*A[i] <= A[j]*A[j]){
result[k--] = A[j]*A[j];
j--;
}
else{
result[k--] = A[i]*A[i];
i++;
}
}
return result;
}
}; 哈希表题型
代码随想录
哈希表基础
一般哈希表都是用来快速判断一个元素是否出现集合里
当我们遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法
哈希法也是牺牲了空间换取了时间,因为我们要使用额外的数组,set或者是map来存放数据,才能实现快速的查找
哈希函数:把学生的姓名直接映射为哈希表上的索引
为了保证映射出来的索引数值都落在哈希表上,我们会在再次对数值做一个取模的操作,就要我们就保证了学生姓名一定可以映射到哈希表上了
哈希碰撞:解决办法:拉链法和线性探测法
拉链法:发生冲突的元素都被存储在链表中。 这样我们就可以通过索引找到小李和小王
拉链法:选择适当的哈希表的大小,这样既不会因为数组空值而浪费大量内存,也不会因为链表太长而在查找上浪费太多时间
线性探测法
线性探测法,一定要保证tableSize大于dataSize。 我们需要依靠哈希表中的空位来解决碰撞问题
冲突的位置,放了小李,向下找一个空位放置小王。所以要求tableSize一定要大于dataSize ,要不然哈希表上就没有空置的位置来存放 冲突的数据
常见的三种哈希结构
数组
set (集合)
map(映射)
无序set、无序map 底层实现为 哈希表
集合 |
底层实现 |
是否有序 |
数值是否可以重复 |
能否更改数值 |
查询效率 |
增删效率 |
std::set |
红黑树 |
有序 |
否 |
否 |
O(log n) |
O(log n) |
std::multiset |
红黑树 |
有序 |
是 |
否 |
O(logn) |
O(logn) |
std::unordered_set |
哈希表 |
无序 |
否 |
否 |
O(1) |
O(1) |
std::unordered_set底层实现为哈希表,std::set 和std::multiset 的底层实现是红黑树,红黑树是一种平衡二叉搜索树,所以key值是有序的,但key不可以修改,改动key值会导致整棵树的错乱,所以只能删除和增加
映射 |
底层实现 |
是否有序 |
数值是否可以重复 |
能否更改数值 |
查询效率 |
增删效率 |
std::map |
红黑树 |
key有序 |
key不可重复 |
key不可修改 |
O(logn) |
O(logn) |
std::multimap |
红黑树 |
key有序 |
key可重复 |
key不可修改 |
O(log n) |
O(log n) |
std::unordered_map |
哈希表 |
key无序 |
key不可重复 |
key不可修改 |
O(1) |
O(1) |
std::unordered_map 底层实现为哈希表,std::map 和std::multimap 的底层实现是红黑树。同理,std::map 和std::multimap 的key也是有序的
当我们要使用集合来解决哈希问题的时候,优先使用unordered_set,因为它的查询和增删效率是最优的,如果需要集合是有序的,那么就用set,如果要求不仅有序还要有重复数据的话,那么就用multiset。
那么再来看一下map ,在map 是一个key value 的数据结构,map中,对key是有限制(key值不可以更改),对value没有限制的,因为key的存储方式使用红黑树实现的。
242. 有效的字母异位词
class Solution{
public:
bool isAnagram(string s,string t){
int record[26] = {0};//因为数值连续,用数组来做哈希表,而不是map//定义哈希表map,索引key为s[i]-'a',键值value=record[key]=字符出现的次数
for(int i = 0;i< s.size();i++){
record[s[i]-'a']++;//在数组中记录s字符串出现的字符个数
}
for(int j = 0;j349. 两个数组的交集
class Solution{
public:
vector intersection(vector& nums1,vector& nums2){
unordered_set result_set;//输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。unordered_set无序,无重复元素,
unordered_set nums(nums1.begin(),nums1.end()); //unordered_set将nums1,转化无序,无重复的元素集合
for(int num : nums2){
if(nums.find(num) != nums.end()){//遍历另一个数组,find()查找nums是否存在该元素
result_set.insert(num);//set 插入一个元素
}
}
return vector (result_set.begin(),result_set.end()); //返回vector() 元素
}
};
//一个数组转化为无序,无重复的unordered_set哈希表
//另一个数组 遍历,比比较查找,放进结果unordered_set结果集 202. 快乐数
class Solution{
public:
int getsum(int n){//计算n的各位数的和
int sum =0;
while(n){
sum += (n%10) * (n%10); //先计算个位数的和
n /= 10;//再计算十位数的和 while(n)
}
return sum;
}
bool isHappy(int n){
unordered_set set; //结果集无序,无重复 unordered_set
while(1){
int sum = getsum(n);//计算操作数和
if(sum==1){//最终循环为快乐树
return true;
}
if(set.find(sum) != set.end()){//在集合unordered_set找到了重复数,死循环
return false;
}
else{
set.insert(sum);//insert插入
}
n =sum; //下一轮n循环
}
}
};//无限循环,那么也就是说求和的过程中,sum会重复出现,这对解题很重要 1. 两数之和
class Solution {
public:
vector twoSum(vector& nums, int target) {
unordered_map map;
for(int i = 0;i < nums.size();i++){
auto it = map.find(target-nums[i]); //返回位置的迭代器 i=1 遍历到7,it迭代器指向哈希表的第一位
if(map.find(it) != map.end()) return {it->second,i}; //{0,1}
else{
map.insert({nums[i],i});
}
}
return {};
}
}; 454. 四数相加 II
首先定义 一个unordered_map,key放a和b两数之和,value 放a和b两数之和出现的次数。
遍历大A和大B数组,统计两个数组元素之和,和出现的次数,放到map中。
定义int变量count,用来统计 a+b+c+d = 0 出现的次数。
在遍历大C和大D数组,找到如果 0-(c+d) 在map中出现过的话,就用count把map中key对应的value也就是出现次数统计出来。
最后返回统计值 count 就可以了
道题目是四个独立的数组,只要找到A[i] + B[j] + C[k] + D[l] = 0就可以,不用考虑有重复的四个元素相加等于0的情况
class Solution {
public:
int fourSumCount(vector& nums1, vector& nums2, vector& nums3, vector& nums4) {
unordered_map map;
for(int a : nums1){
for(int b : nums2){
map[a+b]++; //统计两个值的 次数
}
}
int count = 0;
for(int c : nums3){
for(int d : nums4){
if(map.find(0-(c+d)) != map.end()){ //和-新的两值 出现在哈希表 ,统计次数
count += map[0-(c+d)];
}
}
}
return count;
}
}; 383. 赎金信
class Solution {
public:
bool canConstruct(string ransomNote, string magazine) {
int res[26] = {}; //数组哈希
if(ransomNote.size() > magazine.size()) return false;
for(int i = 0;i < magazine.size();i++){
res[magazine[i] - 'a']++;
}
for(int j = 0; j < ransomNote.size();j++){
res[ransomNote[j] - 'a']--; //数组哈希抵消 思想
if(res[ransomNote[j] - 'a'] < 0){ //ransomNote 里面多了
return false;
}
}
return true;
}
};字符串题型
代码随想录
541. 反转字符串 II
class Solution{
public:
void reverse(string& s,int start,int end){//反转字符串思路
for(int i = start,j=end;i剑指 Offer 05. 替换空格
双指针
151. 反转字符串中的单词
双指针
剑指 Offer 58 - II. 左旋转字符串
//依次局部反转,再整体反转
class Solution{
public:
string reverseLeftWords(string s,int n){
reverse(s.begin(),s.begin()+n); //下标0 到n-1 反转,n=2,(0,1)反转 s.begin()+n末尾元素的下一个元素,下标取前一个数
reverse(s.begin()+n,s.end()); //从n到最后一个元素
reverse(s.begin(),s.end());
return s;
}
};459. 重复的子字符串
//判断一个词是不是子字符串是不是重复构成,可以构建两个词,删除首尾,find查找是否出现词
class Solution {
public:
bool repeatedSubstringPattern(string s) {
string str = s + s;
str = str.substr(1,str.size()-2);
if(str.find(s) == -1 ) return false; //str.find(s)返回下标
return true;
}
};
28. 找出字符串中第一个匹配项的下标
class Solution {
public:
int strStr(string haystack, string needle) {
return haystack.find(needle); 返回匹配的下标
}
};
//暴力
class Solution {
public:
int strStr(string haystack, string needle) {
int m = haystack.size(),n = needle.size();
for(int i = 0;i+n <= m;i++){
bool flag = true;
for(int j = 0;j < n;j++){
if(haystack[i+j] != needle[j]){ //字符串不匹配
flag = false;
break;
}
}
if(flag){
return i;
}
}
return -1;
}
};二分题型
704. 二分查找
//模板六 蓝红二分查找 左开右开,相邻终止,左定右定
//目标值在左边 目标值存在返回下标(说明不一定存在) 需要后续处理
class Solution {
public:
int search(vector& nums, int target) {
const int n = (int)nums.size();
int l = -1, r = n;
while (l+1 != r) {
int mid = l+(r-l)/2;
if (nums[mid] < target) { // isBlue(mid)
l = mid;//中间值和目标值相等了,左指针也移动到mid指针,此时左指针指向的值就是目标值,后续处理处理左指针
} else {
r = mid;
}
}
//后续处理处理右指针 //处理左指针都差不多
if ( r != n && nums[r] == target) { // 后续处理 不越界并且相等
return r;
}
return -1;
}
}; 209. 长度最小的子数组
前缀和+二分
//解法二 前缀和
class Solution{
public:
int minSubArrayLen(int s,vector& nums){
if(nums.size() == 0) return 0;
int n = nums.size();
int ans = INT_MAX;
vector preNums(n+1);//包括下标索引0
for(int i = 0;i>1;
if(preNums[mid] >= t){ //在红区找,返回满足时的r,preNums[r] - preNums[i] >= s(目标值) 前缀和的两值之差就是 区间和本身 区间数量r-i
// pre_sum[mid] - pre_sum[i] >= target 满足要求,mid继续小
// pre_sum[mid] - pre_sum[i] 表示[i,mid]区间的连续和 pre_sum[i]当前i 找合理的mid 下标
r = mid;
}else{
l = mid;
}
}
if(r != n+1){
ans = min(ans,r-i);//i在preNums数组移动,符合子数组长度 更小最小值
}
}
return ans == INT_MAX ? 0:ans;
}
}; //蓝红二分(目标值取左left)有向下取整值得功能 取目标值2.3得左边值 蓝红量身定做 相邻终止left + 1 = right
class Solution {
public:
int mySqrt(int x) {
long long l = -1, r = (long long)x+1; // [0,x]
while (l+1 != r) {
long long mid = (l+r)>>1;
if (mid*mid <= x) {//x为目标值 取左,相等时l左指针指向中间下标 因为小数向下取整 [2.3] mid=2.3,取左边的下标值 2 (目标值取左left)有向下取整值得功能
l = mid;
} else {
r = mid;
}
}
return (int)l;//x为目标值 取左,相等时l左指针指向中间下标 因为小数向下取整
}
};374. 猜数字大小
//中间值是目标,返回目标本身,中间值在目标左边,左边界收缩,继续二分找目标,最后跳出循环,right < left
//蓝红二分法 目标元素划分在左
class Solution {
public:
int guessNumber(int n) {
long long l = 0, r = (long long)n+1;
while (l+1 != r) {
int mid = l+(r-l)/2;
if (guess(mid) >= 0) {//目标值 大于等于 中间值
l = mid;
} else {
r = mid;
}
}
return l;
}
};35. 搜索插入位置
class Solution {
public:
int searchInsert(vector& nums, int target) {
int l = -1,r = nums.size();
while(l + 1 < r){
int mid = (l+r)>>1;
if(nums[mid] < target){
l = mid;
}else{
r = mid; //倾向于取右边
}
}
return r ;
}
}; 852. 山脉数组的峰顶索引
class Solution {
public:
int peakIndexInMountainArray(vector& arr) {
const int n = (int)arr.size();
int l = -1, r = n;
while (l+1 != r) {
int mid = l+(r-l)/2;
if (arr[mid] >= arr[mid+1]) {
r = mid;//峰值 让右指针指向
} else {
l = mid;
}
}
return r;
}
};
367. 有效的完全平方数
class Solution {
public:
bool isPerfectSquare(int num) {
long long l = 0,r = (long long)num+1;
while(l + 1 < r){
long long mid = (l+r)>>1;
if(mid * mid >= num){
r = mid;
}else{
l = mid;
}
}
return r*r == num;
}
};69. x 的平方根
class Solution {
public:
int mySqrt(int x) {
long long l = -1, r = (long long)x+1; // [0,x]
while (l+1 != r) {
long long mid = (l+r)>>1;
if (mid*mid <= x) {//x为目标值 取左,相等时l左指针指向中间下标 因为小数向下取整 [2.3] mid=2.3,取左边的下标值 2 (目标值取左left)有向下取整值得功能
l = mid;
} else {
r = mid;
}
}
return (int)l;//x为目标值 取左,相等时l左指针指向中间下标 因为小数向下取整
}
};278. 第一个错误的版本
class Solution {
public:
int firstBadVersion(int n) {
long long l = 0,r = (long long)n + 1;
while(l +1 < r){
long long mid = (l+r)>>1;
if(isBadVersion(mid)){
r = mid;
}else{
l = mid;
}
}
return r;
}
};441. 排列硬币
//k 行总数(等差数列和) k*(k+1)/2 <= total(完整)
//第0行到第k行 选一行mid
class Solution {
public:
int arrangeCoins(int n) {
long long l = 0,r = (long long)n+1;
while(l+1 < r){
long long mid = l + (r-l)/2;
if(mid*(mid+1) <= 2*(long long)n){
l = mid;
}else{
r = mid;
}
}
return l;
}
};中等
875. 爱吃香蕉的珂珂
//比较值在h时间,计算某个速度所花的时间
// 比较 时间h 先用mid速度算时间
class Solution {
public:
int minEatingSpeed(vector& piles, int h) {
long n = piles.size();
long long l = 0,r = *max_element(piles.begin(),piles.end()) + 1;
while(l + 1 < r){
long long mid = (l + r)>>1;
long time = 0;
for(int pile : piles){
time += (pile - 1 + mid) / mid;//向上取整
}
if(time > h){ //吃的太慢了,加点速度
l = mid;
}else{
r = mid;
}
}
return r;
}
}; 1760. 袋子里最少数目的球
//数组元素 大于 拆值mid,才拆,向下取整 开销值理解为拆值 拆值越小,拆的次数越多
class Solution {
public:
int minimumSize(vector& nums, int maxOperations) {
int n = nums.size();
//l r 代表拆值范围
int l = 0,r = *max_element(nums.begin(),nums.end())+1;
while(l+1>1;
//拆次数 累加(向下取整) 数组5 ,拆值5,不需要拆,数组6,拆值5,拆一次[5,1]
for(auto x : nums){
times += (x-1)/mid;
}
//拆的次数大于目标操作次数 二分调整
if(times > maxOperations){
l = mid;
}else{
r = mid;
}
}
return r;
}
}; 2064. 分配给商店的最多商品的最小
//分开讨论x 更靠近arr数组的 [mid,mid+k];
class Solution {
public:
vector findClosestElements(vector& arr, int k, int x) {
int n = arr.size();
int l = -1,r = n-k;//在区间[0,n-1-k]二分 「最优区间的右边界(返回r)」的下标的搜索区间为 [0, n - k]。
//假设一共有 5 个数,不管 x 的值是多少,在 [0, 1, 2, 3, 4],找 k = 3 个数,左边界(本题理解为右边界)最多到 2;
while(l + 1 < r){
int mid = (l+r)>>1;
if(x-arr[mid] <= arr[mid+k] -x){//x越靠近arr[mid] 还可以更小点
r = mid;
}else{
l = mid;
}
}
return vector(arr.begin()+r,arr.begin()+r+k);
}
}; 1894. 找到需要补充粉笔的学生编号
//前缀和+蓝红二分
class Solution {
public:
int chalkReplacer(vector& chalk, int k) {
int n = chalk.size();
vector preNums(n+1);//定义前缀和
for(int i =0;i < n;i++){
preNums[i+1] = preNums[i] + chalk[i];
if(preNums[i+1] > k){//preNums 下标i+1 对应 chalk下标i
return i;
}
}
k %= preNums.back();//k预处理,处理最后一轮 25%10 = 5(目标值)
int l = -1,r = n;//[0,n-1] 区间二分 在chalk数组
while(l+1 < r){
int mid = (l+r)>>1;
if(preNums[mid+1] > k){//需要粉笔数 > 剩余粉笔数k ,往前小点
r = mid;
}else{
l = mid;
}
}
return r;
}
};
class Solution {
public:
int chalkReplacer(vector& chalk, int k) {
int n = chalk.size();
vector pre(n+1,0);
for(int i = 0;i < n;i++){
pre[i+1] = pre[i] + chalk[i];
if(pre[i+1] > k){ //需求量 > 剩余粉笔量
return i;
}
}
k %= pre.back(); //直接预处理到 末尾
int l = -1,r = n;
while(l + 1 < r){
int mid = (l+r)>>1; //补充下标
if(pre[mid+1] > k){ //需求量 > 剩余粉笔量 r可以再小点
r = mid;
}else{
l = mid;
}
}
return r;
}
}; 2187. 完成旅途的最少时间
class Solution {
public:
long long minimumTime(vector& time, int totalTrips) {
sort(time.begin(),time.end()); // 自小到大排序
long long l = 0,r = (long long)totalTrips * *max_element(time.begin(),time.end());
while(l + 1 < r){
long long mid = (l+r)>>1; //设置完成旅途的时间
long times = 0;
for(int t : time){
if(mid < t) break;
times += mid/t; //完成的旅途的数目
}
if(times >= totalTrips){ //完成的旅途的数目多余目标的 ,可以少点时间
r = mid;
}else{
l = mid;
}
}
return r;
}
};
//规定时间 mid = 3时 ,第1号车 1个小时完成一趟旅途,3个小时内可以走3趟旅途地,第二号车3个小时内可以走1趟旅途地(3/2=1)
//规定时间内,每号车可以完成的旅途地的数 2226. 每个小孩最多能分到多少糖果
class Solution {
public:
int maximumCandies(vector& candies, long long k) {
long long l = 0,r = *max_element(candies.begin(),candies.end()) + 1;
while(l + 1 < r){
long long mid = (l+r)>>1; //设置糖果数
long long times = 0;
for(int i : candies){
times += i / mid; // 分的孩子数
}
if(times >= k){ // 分的多了, 少点,mid加大
l = mid;
}else{
r = mid;
}
}
return l;
}
}; 287. 寻找重复数
class Solution {
public:
int findDuplicate(vector& nums) {
int l = 0,r = nums.size();
while(l + 1 < r){
int mid = (l+r)>>1;
int times = 0;
for(int i : nums){
times += (i <= mid);
}
if(times > mid){ // <=mid 的次数 大于 mid本身 找到重复数 times==mid 不代表找到 mid=4,times=5
r = mid;
}else{
l = mid;
}
}
return r;
}
}; 1283. 使结果不超过阈值的最小除数
class Solution {
public:
int smallestDivisor(vector& nums, int threshold) {
long long l = 0,r = *max_element(nums.begin(),nums.end());
while(l + 1 < r){
long long mid = (l+r)>>1; //设置 除数
long long times = 0;
for(int i : nums){
times += (i-1 + mid)/mid; // 除数阈值
}
if(times > threshold){ // 除数阈值大了,设小点
l = mid;
}else{
r = mid;
}
}
return r;
}
}; 1552. 两球之间的磁力
//最大化的最小磁力 所有集合中,最小磁力的最大[3,3,6] 、[2,4,6] 这两个集合,最小磁力的最大是3
class Solution {
public:
bool check(vector& position,int m,int mid){
int pre = position[0],cnt = 1; //球的数量
for(int i =1;i < position.size();i++){
if(position[i] - pre >= mid){
pre = position[i];
cnt++; // i 位置放一个球
}
}
return cnt >= m; // 放的球的数量来衡量 放的球量大于等于目标球,说明mid磁力小了,需要大点
}
int maxDistance(vector& position, int m) {
sort(position.begin(),position.end());
int l = 0 ,r = *max_element(position.begin(),position.end()) + 1;
while(l + 1 < r){
int mid = (l+r)>>1; //设置磁力
if(check(position,m,mid)){
l = mid;
}else{
r = mid;
}
}
return l;
}
}; 1870. 准时到达的列车最小时速
class Solution {
public:
bool check(vector& dist,double hour,int speed){
int times = 0;
for(int i = 0;i& dist, double hour) {
int l = 0,r = 1e7 + 1;//[1,1e7] 速度
while(l + 1 < r){
int mid = (l+r)>>1;
if(check(dist,hour,mid)){//这个速度满足的话,试探再小一点
r = mid;
}else{
l = mid;
}
}
return r == 1e7+1 ? -1 : r;//时间越界!!!
}
}; 1870. 准时到达的列车最小时速
class Solution {
public:
bool check(vector& dist,double hour,int speed){
double times = 0;
for(int i = 0;i < dist.size()-1;i++){
times += (dist[i] - 1 + speed) / speed; //向上取整
}
double last_time = dist.back() * 1.0 / speed; // 最后时间单独处理
return times + last_time <= hour; // 满足,不断缩进目标hour
}
int minSpeedOnTime(vector& dist, double hour) {
int l = 0,r = 1e7 + 1;
while(l + 1 < r){
int mid = (l+r)>>1; //设置速度
if(check(dist,hour,mid)){ //满足,速度可更慢点
r = mid;
}else{
l = mid;
}
}
return r == 1e7 + 1 ? -1 : r;
}
}; 1898. 可移除字符的最大数目
class Solution {
public:
bool check(string s,string p,vector& removable,int k){
for(int i = 0;i& removable) {
int n = removable.size();
int l = -1, r = n + 1;//[0,n] 出一个整数 k(0 <= k <= removable.length)
while(l+1 < r){
int mid = (l+r)>>1; //设置删除数目(从removavle 0开始)
if(check(s,p,removable,mid)){//mid可以再多点
l = mid;
}else{
r = mid;
}
}
return l;
}
}; 1482. 制作 m 束花所需的最少天数
class Solution {
public:
int check(vector& bloomDay,int k,int targetday){
int bouquests = 0;//几个花束
int flowers = 0;//一个花束 几朵花
for(int day : bloomDay){
if(day > targetday){//day天 大于设置花期,清零
flowers = 0;//置零(相邻连续的)
}else{
++flowers;
if(flowers == k){//相邻花量==k
++bouquests;//一个花束
flowers = 0;
}
}
}
return bouquests;
}
int minDays(vector& bloomDay, int m, int k) {
int l = *min_element(bloomDay.begin(),bloomDay.end()) - 1;
int r = *max_element(bloomDay.begin(),bloomDay.end()) + 1; //[min,max] mid 取开花时间
while(l + 1 < r){
int mid = (l + r)>>1; //设置天数 求花束量
int mbouqust = check(bloomDay,k,mid);//制作几个花束
if(mbouqust >= m){//满足条件,降低开花时间m,接近临界值 m
r = mid;
}else{
l = mid;
}
}
return r == *max_element(bloomDay.begin(),bloomDay.end()) + 1 ? -1:r; //利用边界条件来判断-1
}
}; 658. 找到 K 个最接近的元素
class Solution {
public:
vector findClosestElements(vector& arr, int k, int x) {
int n = arr.size();
int l = -1,r = n - k; //二分找左边界下标,[0,n-k-1]
while(l+1 < r){
int mid = (l+r)>>1; //mid 找最佳左边界下标
if(x - arr[mid] <= arr[mid+k] - x){ // x 属于 [arr[mid],arr[mid+k]] 之间 x离arr[mid]越近
r = mid;
}else{
l = mid;
}
}
return vector(arr.begin()+r,arr.begin()+r+k);
}
}; LCP 12. 小张刷题计划
//[最大值的最小化] 多个集合,选一个最优集合
class Solution {
public:
int minTime(vector& time, int m) {
int l = -1;
if(time.size() < m) return 0;
int ans = 0;
for(int i = 0;i>1; //设置耗时 求天数
if(check(time,mid,m)){//每天设定的目标时 能在要求天数m前 <= m完成, 可提高时间mid l = mid,(每天时间少,花的天数多,每天时间多,花的天数少,可提前完成)
r = mid;
}else{
l = mid;
}
}
return r;
}
bool check(vector& time,int target,int m){
//第一天,使用了同学代写删除
int use_day = 1;//天数
int cur_sum = 0;//所花时间
int cur_max = time[0];//维护最大时间
bool delete1 = true;//使用代写 所花时间清空
for(int i = 0;i target){//超时
if(delete1){//第一天 执行删除最大时间
//减去耗时最多的题目
cur_sum -= cur_max;//变为 满足不超时条件
delete1 = false;//更新为不使用
}else{
//第二天开始 使用同学代写删除,更新为true,i--,留给第二天的下一趟处理
use_day++;
cur_max = 0;
cur_sum = 0;
delete1 = true;
i--;
}
}
}
return use_day <= m;//满足条件 说明每天按照mid时间 可以在m天数之前完成题目
}
}; 410. 分割数组的最大值
//多个两个数组的和最大值(选小的) [7]、[2,5,10,8] 25 | [7,2,5]、[10,8] 18 选18
class Solution {
public:
int splitArray(vector& nums, int k) {
int maxNum = 0,curNum = 0;
for(int x : nums){
maxNum = max(x,maxNum);
curNum += x;
}
int l = maxNum-1;//[0,curNum] 目标值取不到0,连续子数组和 必须从数组最大值开始为l
int r = curNum + 1;//[maxNum,curNum]区间二分 连续子数组的和 充当 目标mid = 开销值 = 速度
while(l + 1 < r){
int mid = (l+r) >> 1;//设置最大值
int splits = check(mid,nums);
if(splits <= k){//子数组数满足, mid连续和 试探再小,分割次数再多一点点靠近边界k
r = mid;
}else{
l = mid;
}
}
return r;
}
int check(int target,vector& nums){
int splits = 1;//分割次数 就是子数组数
int curNum = 0;
for(auto x : nums){
if(curNum + x > target){//不符合条件 当前和清零 分割次数加一
curNum = 0;
splits++;
}
curNum += x;
}
return splits;
}
};
class Solution {
public:
int splitArray(vector& nums, int k) {
int l = *max_element(nums.begin(),nums.end()) - 1;
int r = accumulate(nums.begin(),nums.end(),0) + 1;
while(l + 1 < r){
int mid = (l+r)>>1; //设置最大值
if(check(nums,k,mid) <= k){ //两个连续数组为标准
r = mid;
}else{
l = mid;
}
}
return r;
}
int check(vector& nums,int k,int mid){
int spilit = 1;// 一个连续数组
int sum = 0;
for(int i = 0;i < nums.size();i++){
if(sum + nums[i]> mid){
spilit++;
sum = 0;
}
sum += nums[i];
}
return spilit; //两个连续数组
}
}; DP题型
代码随想录
动态规划基础
确定dp数组(dp table)以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序
举例推导dp数组
区分多少种,还是选一种
vector
基础dp
509. 斐波那契数
class Solution{
public:
int fib(int n){
if(n < 2) return n;//n = 0 1 返回本身
//确定dp数组及下标的含义
vector dp(n+1);//从0开始 空间复杂度为o(n)
dp[0] = 0; //初始化,dp[i] 表示从第i个元素的dp[i]值
dp[1] = 1;
//遍历从前往后遍历
for(int i = 2;i <=n;i++){
dp[i] = dp[i-1] + dp[i-2];//确定状态转移公式
cout< 70. 爬楼梯
爬楼梯是多种方法加起来,使用最小花费爬楼梯选择一种方法(代价最小)
//到i层,有dp[i]种方法
class Solution {
public:
int climbStairs(int n) {
if(n <= 2) return n;
vector dp(n+1);
dp[1] = 1;
dp[2] = 2;
for(int i = 3;i<=n;i++){
dp[i] = dp[i-1] + dp[i-2];
//到第i-1层 有dp[i-1]种方法,在此基础上,再跳一步就到i层,归为dp[i-1]种方法
//到第i-2层 有dp[i-2]种方法,在此基础上,再跳两步就到i层,归为dp[i-2]种方法
}
return dp[n];
}
};
//进阶版
class Solution {
public:
int climbStairs(int n) {
vector dp(n + 1, 0);
dp[0] = 1;
for (int i = 1; i <= n; i++) { // 遍历背包
for (int j = 1; j <= m; j++) { // 遍历物品 一步m个台阶
if (i - j >= 0) dp[i] += dp[i - j];
}
}
return dp[n];
}
}; 746. 使用最小花费爬楼梯
//dp[i]的定义:到达第i台阶所花费的最少钱为dp[i]
class Solution {
public:
int minCostClimbingStairs(vector& cost) {
vector dp(cost.size()+1);
//到达第i层 最小代价dp[i]
dp[0] = 0;
dp[1] = 0;
for(int i = 2;i <= cost.size();i++){
dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
}
return dp[cost.size()]; //跳到dp[9]楼顶 数组8个元素
}
}; 62. 不同路径
class Solution {
public:
int uniquePaths(int m, int n) {
//到对应位置 有dp[i][j]种路径
vector> dp(m,vector(n,0));
for(int i = 0;i 63. 不同路径 II
class Solution {
public:
int uniquePathsWithObstacles(vector>& obstacleGrid) {
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
if(obstacleGrid[0][0] == 1 || obstacleGrid[m-1][n-1] == 1) return 0;
vector> dp(m,vector(n,0));
for(int i = 0;i 343. 整数拆分
class Solution {
public:
int integerBreak(int n) {
//拆i 得到最大乘积dp[i] (好几种拆分方案选一种)
vector dp(n+1);
dp[2] = 1;
for(int i = 3;i<=n;i++){
//j为拆分数
for(int j = 1;j<=i/2;j++){
dp[i] = max(dp[i],max((i-j)*j,dp[i-j]*j)); //max(dp[i],好几个版本更新dp[i])) 拆两个,拆两个以上
}
}
return dp[n];
}
}; 96. 不同的二叉搜索树
// i个元素 有dp[i]个种树
class Solution {
public:
int numTrees(int n) {
vector dp(n+1);
dp[0] = 1;
for(int i = 1;i <= n;i++){ //遍历到n
for(int root_y = 1; root_y <= i;root_y++){
dp[i] += dp[root_y-1] * dp[i-root_y]; //以root_y 为根节点,左子树元素个数为root_y-1个,右子树为i-root_y个
// dp[左子树个数]*dp[右子树个数] 的累加
}
}
return dp[n];
}
}; 背包系列
01背包理论基础
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
每一件物品其实只有两个状态,取或者不取,所以可以使用回溯法搜索出所有的情况,那么时间复杂度就是$o(2^n)$,这里的n表示物品数量。
二维dp数组01背包
确定dp数组以及下标的含义
dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少
通俗:从i里面取 放进j背包里面 拿到最大钱
理解:能放物品就有钱,放物品考虑自身重量,能不能放的进背包
确定递推公式
两个方向推出来dp[i][j],
不取物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以被背包内的价值依然和前面相同。)
取物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
dp[i - 1][j - weight[i]] 从0 - i-1物品中任意取放进背包j - weight[i] 里面,最大钱,当前取i物品放进背包,+value[i] ====放当前i物品,想想之前的dp最大钱
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
dp数组如何初始化
dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],放不进物品,没钱
for (int j = 0 ; j < weight[0]; j++) {
// 当然这一步,如果把dp数组预先初始化为0了,这一步就可以省略,但很多同学应该没有想清楚这一点。
dp[0][j] = 0;
}
// 正序遍历 背包从 weight[0] 0号物品重量开始 到背包容量
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}// 初始化 dp
//j 背包从0开始,数组得bagweight + 1
vector> dp(weight.size(), vector(bagweight + 1, 0));
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
} 确定遍历顺序
先遍历 物品还是先遍历背包重量呢
// weight数组的大小 就是物品个数
//取物品0,依次放进不同容量的背包j,再取物品1
for(int i = 1; i < weight.size(); i++) { // 遍历物品
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j]; //不放 i物品
//放 i物品 max(不放i,放i)
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
// weight数组的大小 就是物品个数
// 给定背包0容量,依次放不同物品,再定背包1
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
for(int i = 1; i < weight.size(); i++) { // 遍历物品
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}void test_2_wei_bag_problem1() {
vector weight = {1, 3, 4};
vector value = {15, 20, 30};
int bagweight = 4;
// 二维数组
vector> dp(weight.size(), vector(bagweight + 1, 0));
// 初始化
// 背包j 至少比 物品0的重量 大,放的进
// dp[0][j] 物品0放背包j 最大钱
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品 i=0 已经考虑
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j]; //先判断能否放进背包
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
cout << dp[weight.size() - 1][bagweight] << endl;
}
int main() {
test_2_wei_bag_problem1();
} 01背包理论基础(滚动数组)
一维滚动数组 背包倒序dp[j] 各物品只放进一次
滚动数组条件:上一层可以重复利用,直接拷贝到当前层
递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
把dp[i - 1]那一层拷贝到dp[i]上,dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
与其把dp[i - 1]这一层拷贝到dp[i]上,不如只用一个一维数组了,只用dp[j]
确定dp数组的定义
dp[j]:容量为j的背包,所背的物品最大钱
一维dp数组的递推公式
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
不放物品i,和放物品i
不放物品i dp[j]为 背包j 所背物品最大钱
放物品i dp[j] 为 当前i的钱 + 之前的dp[j-weight[i]]的钱一维dp数组如何初始化
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j],那么dp[0]就应该是0,因为背包容量为0所背的物品的最大价值就是0。
dp[0] 背包为0 放不了物品 没钱
一维dp数组遍历顺序
物品0,放进背包j,背包倒序
导致背包 只放一次物品
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 倒序遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}倒序遍历背包是为了保证物品i只被放入一次!但如果一旦正序遍历了,那么物品0就会被重复加入多次! 正常来说,放完物品0,放完该物品,再去放物品1
dp[2] 物品0(钱15),背包容量为j=2,dp[j]钱为30,相当于物品0放了两个,然而只有一个物品0
!!不可以先倒序遍历背包容量再遍历物品
倒序遍历背包:导致背包只放一个物品
背包j=bagWeight,再依次放物品,每次dp[j] 都会更新,导致dp[j]只有一个物品的钱 dp[4] = 3
但实际上dp[4]还可以通过放物品0和物品2 得到 钱4
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
//定背包bagWeight 依次放物品012,dp[bagWeight]的钱再变 最后只放了一个物品的钱,本来可以多放其他物品多拿的钱
// 背包4 物品(0 1 2下标) 重量 1 2 3 钱1 2 3 dp[j] 0 1 2 3 4 都初始化为0
//最终dp[4] = 3 (只放了物品2,本来还应该是4的,放物品0,2)
}
}一维背包完整代码
//dp[j] 背包容量为j ,所背物品的最大钱
void test_1_wei_bag_problem() {
vector weight = {1, 3, 4};
vector value = {15, 20, 30};
int bagWeight = 4;
// 初始化
dp[j] 从0开始,dp[bagWeight] 为最大钱
// 0-1 背包物品只放一次,不可以正序背包遍历,不可以先背包再物品遍历
vector dp(bagWeight + 1, 0);
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 倒序遍历背包容量
//让背包只放一次物品i (跟放一个物品有区别)
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); //放物品i还是不放
}
}
cout << dp[bagWeight] << endl;
}
int main() {
test_1_wei_bag_problem();
} 背包小总结1
理清楚 背包容量j是什么定义的,物品是什么定义的
问能否能装满背包(或者最多装多少):dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ,对应题目如下:
动态规划:416.分割等和子集
求背包是否正好装满 背包dp[j] 能不能装满 从数组集合选几个物品装满
动态规划:1049.最后一块石头的重量 II
求背包最多能装多少 背包j 装的dp[j]最多重量 从数组集合最多选几个物品
问装满背包有几种方法:dp[j] += dp[j - nums[i]] ,对应题目如下:
动态规划:494.目标和
动态规划:518. 零钱兑换 II 装满背包求组合数,先物品,再背包正序 完全背包问题
动态规划:377.组合总和Ⅳ 装满背包求排列数,先背包,再物品正序 完全背包问题
动态规划:70. 爬楼梯进阶版(完全背包) 装满背包求排列数,先背包,再物品正序(只有1、2可取)
问背包装满最大价值:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ,对应题目如下:
动态规划:474.一和零
问装满背包,最少物品个数:dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ,对应题目如下:
动态规划:322.零钱兑换
动态规划:279.完全平方数
416. 分割等和子集
01背包问题套到本题上来(背包能不能装满问题)
背包的体积为sum / 2
背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
背包如何正好装满,说明找到了总和为 sum / 2 的子集。
背包中每一个元素是不可重复放入。
物品的重量==物品的钱 = nums[i]
这道题目是要找是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
那么只要找到集合里能够出现 sum / 2 的子集总和(选数组里面的几个元素相加得到sum/2 == 类似于从数组里面选几个物品 是否能填满 背包sum/2 容量),就算是可以分割成两个相同元素和子集了。
class Solution {
public:
//背包容量j 得到的钱
//转化为从数组集合里面 选几个物品 装满 sum/2
bool canPartition(vector& nums) {
int sum = 0;
for(int i : nums) sum += i;
if(sum % 2 == 1) return false;
int bagsize = sum / 2;
vector dp(10000+1,0);
dp[0] = 0;
for(int i = 1;i < nums.size();i++){
for(int j = bagsize;j >= nums[i];j--){
dp[j] = max(dp[j],dp[j-nums[i]] + nums[i]);
}
}
return dp[bagsize] == bagsize;
}
}; 1049. 最后一块石头的重量 II
“背包j 装的dp[j]最多钱” == “背包j 装的dp[j]最多重量”
//以sum/2为背包容量,装多少个物品,得到最大钱(得到最大重量)
class Solution {
public:
int lastStoneWeightII(vector& stones) {
int sum = 0;
for(int i : stones) sum += i;
int bagsize = sum / 2;
vector dp(1500+1,0);
dp[0] = 0;
for(int i = 0;i < stones.size();i++){ //i 从0开始
for(int j = bagsize;j >= stones[i];j--){
dp[j] = max(dp[j],dp[j-stones[i]] + stones[i]);
}
}
return (sum-dp[bagsize]) - dp[bagsize];
}
};
//dp[bagsize] 这个bagsize背包装的最多重量
//sum-dp[bagsize] 另一堆的重量 494. 目标和
class Solution {
public:
//dp[j] 填满j容量的背包 ,组合方法为多少
int findTargetSumWays(vector& nums, int target) {
int sum = 0;
for(int i : nums){
sum += i;
}
if(abs(target) > sum) return 0;// -5 2
if((sum + target) % 2 == 1) return 0; // 5 2
int up = (sum + target) / 2;
// 加法和up 减法和down
// up + down = sum
// up - down = target
vector dp(up+1,0); //填满 加法和 背包容量 有多少种方法
dp[0] = 1;//加法和为0 背包容量为0 也有1种组合方法
for(int i = 0;i < nums.size();i++){
for(int j = up;j >= nums[i];j--){
dp[j] += dp[j-nums[i]]; //之前的dp[j-nums[i]] 再考虑nums[i]进去,就是之前的dp种方法
}
}
return dp[up];
}
}; 474. 一和零
转化为 指定背包容量为m ,最多能装几个字符串(物品) 进来 二维n
//dp[m][n]:最多有m个0和n个1的 strs的最大子集 的大小为dp[m][n]。
class Solution {
public:
int findMaxForm(vector& strs, int m, int n) {
vector> dp(m+1,vector(n+1,0));
//先物品,再背包遍历
//判断当前物品(一个字符串)要不要考虑进来+1 子集
for(string str : strs){
int one = 0,zero = 0;
for(char c : str){
if(c == '0') zero++;
else one++;
}
//m , n 为背包容量 装满m 最多有多少物品(能装几个字符串)
for(int i = m;i>=zero;i--){
for(int j = n;j>=one;j--){
dp[i][j] = max(dp[i][j],dp[i-zero][j-one]+1); //不放物品,放物品(一个字符串)
}
}
}
return dp[m][n];
}
}; 背包小总结2
纯 0 - 1 背包 是求 给定背包容量 装满背包 的最大价值是多少。
416. 分割等和子集是求 给定背包容量,能不能装满这个背包。
494. 目标和 是求 给定背包容量,装满背包有多少种方法。
1049. 最后一块石头的重量 II 是求 给定背包容量,尽可能装,最多能装多少个物品(数组元素)
474. 一和零 给定背包容量,最多可以装几个物品(字符串)
完全背包理论基础
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
01背包和完全背包唯一不同就是体现在遍历顺序上
01背包的核心代码
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}01背包内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次。
完全背包的物品是可以添加多次的,所以要从小到大去遍历
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}完全背包中,两个for循环的先后循序,都不影响计算dp[j]所需要的值
先遍历背包在遍历物品,代码如下:
// 先遍历背包,再遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
for(int i = 0; i < weight.size(); i++) { // 遍历物品
if (j >= weight[i]) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
cout << endl;
}// 先遍历物品,在遍历背包
void test_CompletePack() {
vector weight = {1, 3, 4};
vector value = {15, 20, 30};
int bagWeight = 4;
vector dp(bagWeight + 1, 0);
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = weight[i]; j <= bagWeight; j++) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
cout << dp[bagWeight] << endl;
}
int main() {
test_CompletePack();
} // 先遍历背包,再遍历物品
void test_CompletePack() {
vector weight = {1, 3, 4};
vector value = {15, 20, 30};
int bagWeight = 4;
vector dp(bagWeight + 1, 0);
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
for(int i = 0; i < weight.size(); i++) { // 遍历物品
if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
cout << dp[bagWeight] << endl;
}
int main() {
test_CompletePack();
} 518. 零钱兑换 II
class Solution {
public:
//装满 背包,有dp[amount]种方法
int change(int amount, vector& coins) {
vector dp(amount+1,0);
dp[0] = 1;
for(int i = 0;i 377. 组合总和 Ⅳ
//装满j,排序数量为dp[j]
class Solution {
public:
int combinationSum4(vector& nums, int target) {
vector dp(target+1,0);
dp[0] = 1;
for(int j = 0;j <= target;j++){ //背包正序前
for(int i = 0;i < nums.size();i++){//物品正序
if(j >= nums[i] && dp[j] < INT_MAX - dp[j-nums[i]]){ //判断
dp[j] += dp[j-nums[i]];
}
}
}
return dp[target];
}
}; 70. 爬楼梯
//排列个数的完全背包问题 dp[j] 到j层 有多少种方法
//n层有dp[n]种方法 求排列数问题
class Solution {
public:
//爬到n阶 ,有dp[n]种排列方法
int climbStairs(int n) {
vector dp(n+1,0);
dp[0] = 1;
for(int j = 0;j <= n;j++){ //背包正序
for(int i = 1;i < 3;i++){ //物品正序 只有1、2可取
if(j >= i) dp[j] += dp[j-i]; //判断
}
}
return dp[n];
}
}; 322. 零钱兑换
class Solution {
public:
//装满背包j ,最少硬币个数dp[j]
int coinChange(vector& coins, int amount) {
vector dp(amount+1,INT_MAX);
dp[0] = 0;
//跟排列无关,无需先背包再物品
for(int i = 0;i < coins.size();i++){ //物品正序
for(int j = coins[i];j <= amount;j++){//背包正序
if(dp[j-coins[i]] != INT_MAX) dp[j] = min(dp[j],dp[j-coins[i]] + 1); //不考虑物品i,考虑物品i 硬币个数加一
}
}
return dp[amount] == INT_MAX ? -1 : dp[amount];
}
}; 279. 完全平方数
class Solution {
public:
//背包j,填满的最少平方值个数dp[j]
//跟排列没关系
int numSquares(int n) {
vector dp(n+1,INT_MAX);
dp[0] = 0;
//完全背包,正序 重复取
for(int i = 0;i<=n;i++){
for(int j = 1;j*j <= i;j++){ //物品 平方数
if(dp[i-j*j] != INT_MAX){
dp[i] = min(dp[i],dp[i-j*j]+1);
}
}
}
if(dp[n] == INT_MAX) return -1;
return dp[n];
}
}; 139. 单词拆分
class Solution {
public:
bool wordBreak(string s, vector& wordDict) {
//dp[i]表示 以i为尾下标字符串的背包是否填满 可拆分为一个或多个在字典中出现的单词
//填满 完全背包 + 排序问题(先背包,再物品正序)
unordered_set set(wordDict.begin(),wordDict.end());//放在哈希表,以便查找是否存在
vector dp(s.size()+1,false);
dp[0] = true;
for(int j = 1;j<=s.size();j++){//背包
for(int i = 0;i<=j;i++){//非物品,类似用于构成物品的遍历下标
string str = s.substr(i,j-i); //物品
//if([j, i]区间子串str(物品)出现在哈希字典里 && dp[i]是true) 那么 dp[j] = true
//dp[i] 为真,表示能够填满当前物品i为尾下标s字符串的下标,往前推 + str(存在) 推出dp[j] 真
if(dp[i] && set.find(str) != set.end() ){
dp[j] = true;
break;
}
}
}
return dp[s.size()];
}
}; 打家劫舍
198. 打家劫舍
//dp[i] 到第i间房间,偷的最大金额
//状态推导 第i间偷 和 不偷 的最大金额对比 ,dp末端就是最大值
class Solution {
public:
int rob(vector& nums) {
if(nums.size() == 0) return 0;
if(nums.size() == 1) return nums[0];
vector dp(nums.size()) ;
dp[0] = nums[0];
dp[1] = max(nums[0],nums[1]); //第i间 偷与不偷
for(int i = 2;i < nums.size();i++){
dp[i] = max(dp[i-2] + nums[i],dp[i-1]); //第i间钱 偷与不偷
}
return dp[nums.size()-1];
}
}; 213. 打家劫舍 II
//分两个区间摆脱循环,在第一个打家劫舍的基础上 增加了 start,end 下标
class Solution {
public:
int rob(vector& nums) {
if(nums.size() == 0) return 0;
if(nums.size() == 1) return nums[0];
int result1 = caculte(nums,0,nums.size()-2); //分两个区间
int result2 = caculte(nums,1,nums.size()-1);
return max(result1,result2);
}
int caculte(vector& nums,int start,int end){
if(start == end) return nums[start];
vector dp(nums.size());
dp[start] = nums[start];
dp[start+1] = max(nums[start],nums[start+1]);//偷与 不偷(看前)
for(int i = start + 2;i <= end;i++){
dp[i] = max(dp[i-2] + nums[i],dp[i-1]);
}
return dp[end];
}
}; 337. 打家劫舍 III
// result数组定义 下标0 偷 下标1 不偷
class Solution {
public:
int rob(TreeNode* root) {
vector result = traverse(root);
return max(result[0],result[1]);
}
// 递归的定义 返回{偷的最大金额,不偷的最大金额} 后序遍历
vector traverse(TreeNode* root){
if(root == nullptr) return {0,0};
vector left = traverse(root->left); //左
vector right = traverse(root->right);//右
//中逻辑
int val1 = root->val + left[1] + right[1]; //偷根节点
int val2 = max(left[0],left[1]) + max(right[0],right[1]);//不偷根节点 ,偷左右孩子的
return {val1,val2};
}
}; 总结
股票系列
121. 买卖股票的最佳时机
一段时间,只能买卖一次,问最大收益
//dp[i][0] 第i天持有股票的最多钱
//dp[i][1] 第i天不持有股票的最多钱
class Solution {
public:
int maxProfit(vector& prices) {
vector> dp(prices.size(),vector(2));
dp[0][0] = -prices[0]; // 一开始持有,只能买入(不考虑之前状态,之前本来就没有赚钱
dp[0][1] = 0;
for(int i = 1;i < prices.size();i++){
//持有股票 max(昨天持有,今天买入(考虑到当前只买一次,昨天肯定没赚钱,不引入昨天卖出状态))
dp[i][0] = max(dp[i-1][0],-prices[i]);
//不持有状态 max(昨天不持有,今天不持有(今天卖出,昨天肯定持有赚钱))
dp[i][1] = max(dp[i-1][1],dp[i-1][0]+prices[i]);
}
return dp[prices.size()-1][1];
}
}; 00122. 买卖股票的最佳时机 II
//买卖多次,就不考虑 具体几个 2*k+1个状态
class Solution {
public:
int maxProfit(vector& prices) {
int len = prices.size();
if(len == 0) return 0;
vector> dp(len,vector(2));
dp[0][0] = -prices[0];//持有股票状态
dp[0][1] = 0;//不持有股票状态
for(int i = 1;i 123. 买卖股票的最佳时机 III
//买卖2次,就有2*2+1个状态
class Solution {
public:
int maxProfit(vector& prices) {
int len = prices.size();
vector> dp(len,vector(5,0));
dp[0][0] = 0;//不操作
dp[0][1] = -prices[0];//第一次买
dp[0][2] = 0;//第一次卖
dp[0][3] = -prices[0];//第二次买
dp[0][4] = 0;//第二次卖出
for(int i = 1;i < len;i++){
dp[i][0] = 0; //没走流程前 没有利润
//昨天已进该状态、今天才持有该状态(考虑昨天的利润)
dp[i][1] = max(dp[i-1][1],dp[i-1][0] -prices[i]);
dp[i][2] = max(dp[i-1][2],dp[i-1][1] + prices[i]);
dp[i][3] = max(dp[i-1][3],dp[i-1][2] - prices[i]);
dp[i][4] = max(dp[i-1][4],dp[i-1][3] + prices[i]);
}
return dp[len-1][4];
}
}; 188. 买卖股票的最佳时机 IV
//买卖k次,就有2*k+1个状态
class Solution {
public:
int maxProfit(int k, vector& prices) {
int len = prices.size();
vector> dp(len,vector(2*k+1));
for(int i = 1;i <= 2*k;i += 2){
dp[0][i] = -prices[0];
}
for(int i = 1;i < len;i++){
for(int j = 0;j < 2*k-1;j += 2){
dp[i][j+1] = max(dp[i-1][j+1],dp[i-1][j] - prices[i]);//持有
dp[i][j+2] = max(dp[i-1][j+2],dp[i-1][j+1] + prices[i]);//不持有
}
}
return dp[len-1][2*k];
}
}; 309. 最佳买卖股票时机含冷冻期
//dp[i][j] 第i天状态j,所得的最大现金dp[i][j]
class Solution {
public:
//四种状态
//推演: 买 卖 冷冻 买 卖
//0 持有状态 1保持卖出状态 2当前卖出 3冷冻
//不持有状态 分离两个卖出状态
int maxProfit(vector& prices) {
int len = prices.size();
vector> dp(len,vector(4,0));
dp[0][0] = -prices[0];
for(int i = 1;i 714. 买卖股票的最佳时机含手续费
//不持有状态 卖出多了手续费
class Solution {
public:
int maxProfit(vector& prices, int fee) {
int len = prices.size();
vector> dp(len,vector(2));
dp[0][0] = -prices[0];//持有股票状态
for(int i = 1;i 总结
子串(连续)
647. 回文子串
//dp[i][j] 表区间i-j的子串是回文串,dp[i][j] 是回文串true
class Solution{
public:
int countSubstrings(string s){
vector> dp(s.size(),vector(s.size(),false));
//初始化为false ,后面的dp[i][i] 单字符会判断为true
int result = 0;
//从下向上,从左向右 dp[i+1][j-1]
for(int i = s.size()-1;i>=0;i--){ //从下向上
for(int j = i;j < s.size();j++){ //从左向右
//a,aa
if(s[i] == s[j]){
if(j-i <= 1){
result++;
dp[i][j] = true;//后面的dp[i][i] 单字符会判断为true
}
else if(dp[i+1][j-1])//aba
{
result++;
dp[i][j] =true;
}
}
}
}
return result;
}
};
5. 最长回文子串
//dp[i][j] 区间[i,j]为回文连续子串,为true //substr(左边界,个数)
class Solution {
public:
string longestPalindrome(string s) {
vector> dp(s.size(),vector(s.size(),0));
int maxlen = 0,left = 0,right = 0;
for(int i = s.size()-1;i >= 0; i--){
for(int j = i;j < s.size();j++){
if(s[i] == s[j]){
if(j-i <= 1){
dp[i][j] = true;
}else if(dp[i+1][j-1]){
//如果之前dp[i+1][j-1]是真的,现在if(s[i] == s[j]) 也为真
dp[i][j] = true;
}
//分开 当前dp[i][j]
if(dp[i][j] && j-i+1 > maxlen){ //更新最大长度
maxlen = j-i+1;
left = i;
right = j;
}
}
}
}
return s.substr(left,maxlen);
}
}; 516. 最长回文子序列
//dp[i][j] 表i-j区间的回文串子序列的最长长度(不连续,回文子串是连续的)
class Solution{
public:
int longestPalindromeSubseq(string s){
vector> dp(s.size(), vector(s.size(), 0));
for(int i = 0;i < s.size();i++){
dp[i][i] = 1;//相同区间(一个字符)的回文子串的最长长度为1
}
for(int i = s.size() -1;i >= 0;i--){
for(int j = i+1;j < s.size();j++){//j从i+1开始,因为j=i的情况已经考虑过了
if(s[i] == s[j]){
dp[i][j] = dp[i+1][j-1] + 2;//两个回文子串字符
}else {
dp[i][j] = max(dp[i+1][j],dp[i][j-1]);//从[i,j-1]的区间找回文子串的最长长度
}
}
}
return dp[0][s.size()-1]; //整个区间来看
}
};
//dp[i][j] 表示i-j区间的回文子序列的长度(非连续)
class Solution {
public:
int longestPalindromeSubseq(string s) {
vector> dp(s.size(),vector(s.size(),0));
for(int i = 0;i < s.size();i++){
dp[i][i] = 1;
}
for(int i = s.size()-1;i>=0;i--){
for(int j = i+1;j < s.size();j++){
if(s[i] == s[j]){
dp[i][j] = dp[i+1][j-1] + 2;
//不用判断dp[i+1][j-1]是否存在,直接用 不连续回文子序列
}else{
dp[i][j] = max(dp[i+1][j],dp[i][j-1]);
}
}
}
return dp[0][s.size()-1];
}
}; 子序列(不连续)
300. 最长递增子序列
//dp[i] 为到nums[i]结尾的最长递增子序列的长度
class Solution {
public:
int lengthOfLIS(vector& nums) {
if(nums.size() <= 1) return nums.size();
vector dp(nums.size(),1); //dp[i] = 1 单个数也是递增 1
int result = INT_MIN;
for(int i = 0;i < nums.size();i++){
for(int j = 0;j < i;j++){
if(nums[i] > nums[j]){ //连续和不连续的区别
dp[i] = max(dp[i],dp[j]+1); // j之前的最长数列dp[j] +1
}
if(result < dp[i]) result = dp[i];
}
}
return result;
}
}; 674. 最长连续递增序列
class Solution {
public:
int findLengthOfLCIS(vector& nums) {
if(nums.size() <= 1) return nums.size();
vector dp(nums.size(),1);
int result = INT_MIN;
for(int i = 1;i < nums.size();i++){
if(nums[i] > nums[i-1]){ //连续比不连续的处理简单点
dp[i] = max(dp[i],dp[i-1]+1);
}
if(dp[i] > result) result = dp[i];
}
return result;
}
};
//跟最长递增子序列的区别就是 if(nums[i] > nums[j])关系 递推 i和j不挨在一起 718. 最长重复子数组
//dp[i][j] 定义表示 i-1为结尾下标和j-1为结尾下标的最长重复子数组的长度
class Solution {
public:
int findLength(vector& nums1, vector& nums2) {
//左上边界置零
vector> dp(nums1.size()+1,vector(nums2.size()+1,0));
int result = 0;
for(int i = 1;i <= nums1.size();i++){
for(int j = 1;j <= nums2.size();j++){
if(nums1[i-1] == nums2[j-1]){ //连续i,i-1 连续重复 满足递推
dp[i][j] = max(dp[i][j],dp[i-1][j-1]+1);
}
if(dp[i][j] > result) result = dp[i][j];
}
}
return result;
}
}; 1143. 最长公共子序列
//dp[i][j] 定义为 以数组i-1为结尾,j-1为结尾的不连续公共子序列的最长长度
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
//左上边界置零
vector> dp(text1.size()+1,vector(text2.size()+1,0));
for(int i = 1;i <= text1.size();i++){
for(int j = 1;j <= text2.size();j++){
//数组下标为个数-1
//三个状态推
if(text1[i-1] == text2[j-1]){ //相同,+1
dp[i][j] = max(dp[i][j],dp[i-1][j-1]+1);
}else{//不同 从前面的状态推(不要求连续)
dp[i][j] = max(dp[i][j-1],dp[i-1][j]);
}
}
}
return dp[text1.size()][text2.size()]; //dp[下标为个数]
}
};
//子序列 要求不连续,与最长重复子数组的不同就是 多两个状态推出 1035. 不相交的线
//本质在求最长公共子序列,这个子序列不改变相对顺序,相同的数字链接直线不相交
dp[i][j] 定义为 以数组i-1为结尾,j-1为结尾的不连续公共子序列的最长长度
class Solution{
public:
int maxUncrossedLines(vector& nums1,vector& nums2){
vector> dp(nums1.size()+1,vector(nums2.size()+1,0));
//初始化dp[i][0] = 0
//dp[i] 与 nums[i-1] 对应
for(int i = 1;i <= nums1.size();i++){
for(int j = 1;j <= nums2.size();j++){
if(nums1[i-1] == nums2[j-1]){
dp[i][j] = dp[i-1][j-1] + 1;
}
else {
dp[i][j] = max(dp[i-1][j],dp[i][j-1]);//三个方向
}
}
}
return dp[nums1.size()][nums2.size()];
}
}; 392. 判断子序列
//相同公共子序列 的长度类似
//dp[i][j] 定义为 数组下标为i-1,和j-1 的相同公共不连续子序列
class Solution {
public:
bool isSubsequence(string s, string t) {
//左上边界置零
vector> dp(s.size()+1,vector(t.size()+1,0));
for(int i = 1;i <= s.size();i++){
for(int j = 1;j <= t.size();j++){
//递推 找到公共元素 +1
if(s[i-1] == t[j-1]){
dp[i][j] = max(dp[i][j],dp[i-1][j-1]+1);
}else{ //没找到 往前看
dp[i][j] = dp[i][j-1];//长的t 往前看
}
}
}
// 相同公共子序列 长度
if(dp[s.size()][t.size()] == s.size()) return true;
return false;
}
}; 53. 最大子数组和
// dp[i] 为数组下标i-1结尾的 最大和 的连续子数组
class Solution {
public:
int maxSubArray(vector& nums) {
if(nums.size() == 0) return 0;
vector dp(nums.size());
dp[0] = nums[0];//初始化
int result = dp[0]; //result更新最大值,dp[nums.size()-1]从下标0开始,不一定为最大子连续数组和
for(int i = 1;i < nums.size();i++){
//max(前一个状态连续推出,或从新开始)
dp[i] = max(dp[i-1] + nums[i],nums[i]);
if(result < dp[i]) result = dp[i];
}
return result;
}
}; 115. 不同的子序列
//dp[i][j] 定义为 数组下标i-1的s子序列 包含 下标j-1的t子序列 出现的个数
//s中包含t的个数
class Solution {
public:
int numDistinct(string s, string t) {
//左上边界置零 uint64_t
vector> dp(s.size()+1,vector(t.size()+1));
dp[0][0] = 1;
for(int i = 1;i <= s.size();i++) dp[i][0] = 1; //i从1开始遍历
for(int j = 1;j <= t.size();j++) dp[0][j] = 0;
for(int i = 1;i <= s.size();i++){
for(int j = 1;j <= t.size();j++){
if(s[i-1] == t[j-1]){
// s选择匹配 + 不匹配往前看 bagg bag 看定义,s中包含t的个数
dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
}else{//不相同,s向前走 找匹配
dp[i][j] = dp[i-1][j];
}
}
}
return dp[s.size()][t.size()];
}
};
//重在匹配 583. 两个字符串的删除操作
//dp[i][j] 以i-1为下标的word1和word2字符串相同时,最少删除操作数
//两个字符串删成同样的 最小操作数
class Solution {
public:
int minDistance(string word1, string word2) {
//左上边界置零
vector> dp(word1.size()+1,vector(word2.size()+1));
dp[0][0] = 0;
for(int i = 1;i <= word1.size();i++) dp[i][0] = i; //删除成同样的 多需操作数
for(int j = 1;j <= word2.size();j++) dp[0][j] = j;
for(int i = 1 ; i <= word1.size();i++){
for(int j = 1; j <= word2.size();j++){
if(word1[i-1] == word2[j-1]){
//当前相同 不用删,dp为之前的删除数
dp[i][j] = dp[i-1][j-1];
}else{
//不相同,删除操作有三种方式递推 dp为删除后的相同字符串
//删除一个字符 + dp[i-1][j]使两个子串相同的最小操作数
dp[i][j] = min({dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+2});
}
}
}
return dp[word1.size()][word2.size()];//使字符串相同最终的最小操作数
}
};
//动态规划2 先计算出最长公共子序列,再总的长度减去最长公共子序列的两倍就是删除的最小步数
class Solution {
public:
int minDistance(string word1, string word2) {
vector> dp(word1.size()+1, vector(word2.size()+1, 0));
for (int i=1; i<=word1.size(); i++){
for (int j=1; j<=word2.size(); j++){
if (word1[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
}
}
return word1.size()+word2.size()-dp[word1.size()][word2.size()]*2;
}
}; 72. 编辑距离
//dp[i][j] 定义为 两个字符串 变为相同的 最少操作数
//数组 i-1为下标的字符串 和 j-1为下标的字符串 变为相同的最少操作数
class Solution {
public:
int minDistance(string word1, string word2) {
//左上边界置零
vector> dp(word1.size()+1,vector(word2.size()+1));
dp[0][0] = 0;
for(int i = 1;i<=word1.size();i++) dp[i][0] = i; //变一样的最少操作数
for(int j = 1;j<=word2.size();j++) dp[0][j] = j;
for(int i = 1;i <= word1.size();i++){
for(int j =1;j <= word2.size();j++){
//当前相同,不做任何操作,往前看
if(word1[i-1] == word2[j-1]){
dp[i][j] = dp[i-1][j-1];
}else{
//不同,插删替换三种方式变一样
//dp[i][j] 为相同时的最小操作数
//添加和删除 的dp一样 故只考虑删除
dp[i][j] = min({dp[i-1][j] + 1,dp[i][j-1] + 1,dp[i-1][j-1] + 1});
}
}
}
return dp[word1.size()][word2.size()]; //最终变一样的最少操作数
}
}; 子序列总结
最强总结篇
单调栈题型
一维数组,要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置,此时我们就要想到可以用单调栈了。时间复杂度为O(n)
单调栈的本质是空间换时间
在遍历的过程中需要用一个栈来记录右边第一个比当前元素高的元素,优点是整个数组只需要遍历一次
单调栈的顺序:
739. 每日温度中求一个元素右边第一个更大元素,单调栈就是递增的(从栈头到栈底来看)
84.柱状图中最大的矩形 求一个元素右边第一个更小元素,单调栈就是递减的。
代码随想录
739. 每日温度
找到每一个元素的右边第一个比它大的元素位置
//最后栈里面留下的是 单调递增(从栈头到栈顶看)
//result的记录的是每个元素的距离右边第一大的元素下标
class Solution{
public:
vector dailyTemperatures(vector& temperatures){
vector result(temperatures.size(),0);
stack st; //递增单调栈(从栈头到栈底)
st.push(0);//i=0 下标
for(int i = 1;i temperatures[i]){ //栈头元素 没遇到比他大的,不处理
st.push(i);//栈内放的是下标
}
else if(temperatures[st.top()] == temperatures[i]){
st.push(i);
}
else{
//处理栈 要加!st.empty() 73 73(下标已经放入栈顶) 74
while(!st.empty() && temperatures[st.top()] < temperatures[i]){
result[st.top()] = i - st.top();
//先记录栈头下标,对应距离,栈头元素弹出
//记录栈顶元素下标 (当前右边第一大的下标-栈头下标)
st.pop();//退出 栈顶元素下标
}
st.push(i);//入栈
}
}
return result;
}
}; 496. 下一个更大元素 I
class Solution {
public:
vector nextGreaterElement(vector& nums1, vector& nums2) {
vector result(nums1.size(),-1);
if(nums1.size() == 0) return result;
//nums1 建立哈希表
unordered_map map;
for(int i = 0; i < nums1.size();i++){
map[nums1[i]] = i;
}
//nums2 递增单调栈(从栈头到栈底方向)
stack s;
s.push(0);
for(int i = 1;i < nums2.size();i++){
while(!s.empty() && nums2[s.top()] < nums2[i]){ //当前元素 大于栈头,入栈要处理
if(map.count(nums2[s.top()]) > 0){ //栈头元素在nums1数组里面
int index = map[nums2[s.top()]];
result[index] = nums2[i]; //记录当前元素为 nums1栈头元素的 第一大数
}
s.pop();
}
s.push(i);
}
return result;
}
}; 503. 下一个更大元素 II
数组循环,在遍历大小扩容两倍, i%nums.size()
//取模 进行循环遍历 单调栈来求下一个更大值
class Solution{
public:
vector nextGreaterElements(vector& nums){
stack st;
vector result(nums.size(),-1);
if(nums.size() == 0) return result;
for(int i = 0;i < nums.size()*2 ;i++ ){ //扩容两倍数组
while(!st.empty() && nums[st.top()] < nums[i % nums.size()]){ //多出的数组下标 保证在循环数组内
result[st.top()] = nums[i % nums.size()]; //栈顶元素下标对位的result的下标 的下一位更大值
st.pop();//退栈顶元素下标
}
st.push(i%nums.size()); //入当前下标 i=0 栈内为空直接入栈索引下标也可以
}
return result;
}
}; 42. 接雨水
//单调栈 求雨水面积,从栈头到栈尾(递增) 栈内下标
class Solution{
public:
int trap(vector& height){
if(height.size() <= 2) return 0;
stack st;
st.push(0);
int sum = 0;
for(int i = 1;i < height.size();i++){
if(height[i] < height[st.top()]){
st.push(i);
}
else if(height[st.top()] == height[i]){
st.pop();
st.push(i);
}else{
while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while
int mid = st.top();
st.pop();
if (!st.empty()) { //不为空,左边有山,可以算面积 接雨水
int h = min(height[st.top()], height[i]) - height[mid];
int w = i - st.top() - 1; // 注意减一,只求中间宽度 按行来取面积
sum += h * w;
}
}
st.push(i);
}
}
return sum;
}
}; 84. 柱状图中最大的矩形
//单调栈(递减) (从栈头到栈底)
class Solution {
public:
int largestRectangleArea(vector& heights) {
int sum = 0;
stack s;
s.push(0);
//原数组预处理,前后加0,方便计算
heights.insert(heights.begin(),0);
heights.push_back(0);
for(int i = 1; i < heights.size();i++){
if(heights[i] > heights[s.top()]){
s.push(i);
}else if(heights[i] == heights[s.top()]){
s.pop();
s.push(i);
}else{
while(!s.empty() && heights[i] < heights[s.top()]){ //while,只要当前元素小于栈头元素,更新计算sum
int mid = s.top();
s.pop();
int r = i;
int l = s.top();
int h = heights[mid];
int w = r - l - 1;
sum = max(sum,h*w);
}
s.push(i);
}
}
return sum;
}
}; 85. 最大矩形
转化为求每一行的 柱状图的最大矩阵面积
//转化为求每一行的 柱状图的最大矩阵面积
class Solution{
public:
int largestmax(vector height){//此处不能加引用!!!!!! 每一次的height都是新的height数组
height.insert(height.begin(),0);
height.push_back(0);//首尾加0的哨兵
stack st;
st.push(0);//单调栈,栈底到栈顶 由小到大,栈顶遇到更小值进行处理再入栈
int sum = 0;
for(int i = 1;i height[i]){
int mid = st.top();
st.pop();
int w = i - st.top() -1;//此时的st.top()下标为前一位栈顶元素下标
int h = height[mid];
sum = max(sum,h*w);
}
st.push(i);
}
}
return sum;
}
int maximalRectangle(vector>& matrix){
if(matrix.size() == 0) return 0;
int m = matrix.size();
int n = matrix[0].size();
int maxmianji = 0;
vector height(n,0);//每一行的高度记录
for(int i = 0;i 宫水三叶题库
线性DP
650. 只有两个键的键盘
//dp[i] 得到i个 需要的最少操作数
//状态转移:dp[i] = dp[j] + dp[i/j] j为i的整除因数,j == 1排除掉
//6个i 6/2=3 开始AA 操作三次AA AA AA 转化为 A 操作三次A A A
//dp[6] = dp[2] + dp[3]
//dp[2]复制+粘贴 操作两次得到AA 再dp[3]操作三次AA AA AA 得到dp[6]
// 先dp[j]得到j个A + 再dp[i/j]操作 i/j 次
//dp[n] 由小于n 的质数dp[i] 线性表示
class Solution {
public:
int minSteps(int n) {
vector dp(n+1);
for(int i = 2;i <= n;i++){
dp[i] = i; //一步步粘
for(int j = 2;j * j <= i;j++){
if(i % j == 0) dp[i] = dp[j] + dp[i/j]; //i被j 整除的条件下
}
}
return dp[n];
}
}; 688. 骑士在棋盘上的概率(三维dp)
记忆化搜索也是动态规划的一种写法
//棋盘上的同一个位置在剩余 x 次时有可能会重复的到达,所以,我们需要加一个缓存,这也就是记忆化搜索
class Solution {
public:
const int dir[8][2] ={{2,1},{1,2},{-1,2},{-2,1},{-2,-1},{-1,-2},{1,-2},{2,-1}};
double knightProbability(int n, int k, int row, int column) {
vector>> memo(n,vector>(n,vector(k+1,0)));
return dfs(n,k,row,column,memo);
}
double dfs(int n,int k,int x,int y,vector>>& memo){
if(x < 0 || x >= n || y < 0 || y >= n) return 0;
if(k == 0) return 1;
if(memo[x][y][k] != 0) return memo[x][y][k]; //三个维度
double ans = 0;
for(auto e : dir){
int new_x = x + e[0];
int new_y = y + e[1];
ans += dfs(n,k-1,new_x,new_y,memo)/8.0;
}
memo[x][y][k] = ans; //记录 当前位置的概率
return ans;
}
}; 此前有八个位置,而且已经走了k-1步,再走一步,就到了i,j位置和k步,统计当前步数的累加8次概率
三维dp
class Solution {
public:
const int dir[8][2] ={{2,1},{1,2},{-1,2},{-2,1},{-2,-1},{-1,-2},{1,-2},{2,-1}};
double knightProbability(int n, int k, int row, int column) {
vector>> dp(n,vector>(n,vector(k+1,0)));
//dp[i][j][k] 表示走了k步到[i][j]位置的概率
//由前八个位置+已走k-1步的状态 再走一步到i,j,k 来推
//kk在动态规划上是递增
for(int kk = 0;kk <= k;kk++){
for(int i = 0;i < n;i++){
for(int j = 0;j < n;j++){
if(kk == 0){
dp[i][j][kk] = 1;
}else{
for(auto e : dir){
int x = i + e[0];
int y = j + e[1];
if(x >= 0 && x = 0 && y < n){
dp[i][j][kk] += dp[x][y][kk-1]/8.0;
}
}
}
}
}
}
return dp[row][column][k]; //当前位置的概率
}
}; 978. 最长湍流子数组
class Solution {
public:
int maxTurbulenceSize(vector& arr) {
if(arr.size() < 2) return arr.size();
vector> dp(arr.size(),vector(2,1)); //两个状态转移
for(int i = 1;i < arr.size();i++){
if(arr[i] > arr[i-1]){//升序
dp[i][0] = dp[i-1][1] + 1;
}else if(arr[i] < arr[i-1]){//降序
dp[i][1] = dp[i-1][0] + 1;
}
}
int result = 0;
for(int i = 0;i < arr.size();i++){
result = max(result,dp[i][0]);
result = max(result,dp[i][1]);
}
return result;
}
}; Hot100题型
easy
21. 合并两个有序链表
class Solution {
public:
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
if(list1 == nullptr) return list2;
if(list2 == nullptr) return list1;
if(list1->val < list2->val){
list1->next = mergeTwoLists(list1->next,list2);
return list1;
}else{
list2->next = mergeTwoLists(list1,list2->next);
return list2;
}
return nullptr;
}
};136. 只出现一次的数字
class Solution{
public:
int singleNumber(vector& nums){
int result = 0;
for(int i : nums) result ^= i;//^累异或
return result;//0异或本身 = 本身,相同异或为0
}
}; 141. 环形链表
class Solution{
public:
bool hasCycle(ListNode* head){
ListNode* slow = head;
ListNode* fast = head;
while(fast != NULL && fast->next != NULL){
slow = slow->next;
fast = fast->next->next;
if(slow == fast){
return true;//有环,快慢指针一定会相遇
}
}
return false;
}
};206. 反转链表
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(head == nullptr || head->next == nullptr) return head;
ListNode* tmp = reverseList(head->next); //返回的是头节点
head->next->next = head;
head->next = nullptr;
return tmp;
}
};1. 两数之和
class Solution {
public:
vector twoSum(vector& nums, int target) {
unordered_map map;
for(int i = 0;i < nums.size();i++){
auto it = map.find(target-nums[i]);
if(it != map.end()){
return {it->second,i};
}else{
map.insert({nums[i],i});
}
}
return {};
}
}; 20. 有效的括号
class Solution {
public:
bool isValid(string s) {
if(s.size() % 2 == 1) return false;
stack st;
for(int i = 0;i < s.size();i++){
if(s[i] == '('){
st.push(')');
}else if(s[i] == '['){
st.push(']');
}else if(s[i] == '{'){
st.push('}');
}else if(st.empty() || s[i] != st.top() ){ //不匹配
return false;
}else{
st.pop();
}
}
return st.empty(); //判断栈是否为空
}
}; 160. 相交链表
class Solution{
public:
ListNode* getIntersectionNode(ListNode* headA,ListNode* headB){
if(headA == NULL || headB == NULL) return NULL;
int lenA = 0;
int lenB = 0;
ListNode* curA = headA;
ListNode* curB = headB;
while(curA!= nullptr){
lenA++;
curA = curA->next;
}
while(curB != nullptr){
lenB++;
curB = curB->next;
}
if(lenB > lenA){
swap(lenA,lenB);
swap(headA,headB);
}
int gap = lenA - lenB;
while(gap--){
headA= headA->next;//将节点指针指向同B一起
}
while(headA != NULL){
if(headB == headA){//一开始就相同了找到相交节点
return headA;
}else{
headA = headA->next;
headB = headB->next;
}
}
return NULL;
}
};94. 二叉树的中序遍历
//统一迭代法 访问的节点放入栈中,一次,弹出,之后要处理的节点再放入栈中,同时加NULL空节点做标志
//访问节点,处理(放进结果集)
class Solution{
public:
vector inorderTraversal(TreeNode* root){
stack st;
vector result;
if(root != nullptr) st.push(root);
while(!st.empty()){
TreeNode* cur = st.top();
if(cur != NULL){
st.pop();
//右
if(cur->right) st.push(cur->right);
//中 + null标记
st.push(cur);
st.push(nullptr);
//左
if(cur->left) st.push(cur->left);
}else{
//处理空标记前的 中间节点
st.pop();
cur = st.top();
st.pop();
result.push_back(cur->val);
}
}
return result;
}
}; 70. 爬楼梯
class Solution {
public:
//爬到n阶 ,有dp[n]种排列方法
int climbStairs(int n) {
vector dp(n+1,0);
dp[0] = 1;
for(int j = 0;j <= n;j++){ //背包正序
for(int i = 1;i < 3;i++){ //物品正序 只有1、2可取
if(j >= i) dp[j] += dp[j-i]; //判断
}
}
return dp[n];
}
};
class Solution {
public:
int climbStairs(int n) {
if(n <= 1) return 1;
vector dp(n+1);
dp[1] = 1;
dp[2] = 2;
for(int i = 3;i <= n;i++){
dp[i] = dp[i-1] + dp[i-2];
}
return dp[n];
}
}; 155. 最小栈
class MinStack {
public:
MinStack() {
}
void push(int val) {
if(st.empty()){
st.push({val,val});
}else{
st.push({val,min(val,st.top().second)});//辅助栈一个思路
}
}
void pop() {
st.pop();
}
int top() {
return st.top().first;
}
int getMin() {
return st.top().second;
}
stack> st;
}; 104. 二叉树的最大深度
class Solution{
public:
int maxDepth(TreeNode* root){
if(root==NULL) return 0;
int left = maxDepth(root->left);
int right = maxDepth(root->right);
int depth = 1 + max(left,right);
return depth;
}
};
层序遍历,广度优先遍历
class Solution {
public:
int maxDepth(TreeNode* root) {
queue q;
if(root != nullptr) q.push(root);
int dep = 0; //depth在外面
while(!q.empty()){
int size = q.size();
dep++; //每次while当前层 加一次
for(int i = 0;i < size;i++){
TreeNode* cur = q.front();
q.pop();
if(cur->left){
q.push(cur->left);
}
if(cur->right){
q.push(cur->right);
}
}
}
return dep;
}
}; 101. 对称二叉树
class Solution{
public:
bool mycompare(TreeNode* left,TreeNode* right){
if(left == NULL && right == NULL) return true;
if(left == NULL || right == NULL || left->val != right->val) return false;
bool int_compare = mycompare(left->right,right->left); //第二层递归判断
bool out_compare = mycompare(left->left,right->right);
return int_compare&out_compare;
}
bool isSymmetric(TreeNode* root){
if(root == NULL) return true;
return mycompare(root->left,root->right);
}
};
迭代法
class Solution{
public:
//队列来比较两个树是否翻转
bool isSymmetric(TreeNode* root){
if(root==NULL) return true;
queue que;
que.push(root->left);
que.push(root->right);
while(!que.empty()){ //不用size
TreeNode* leftNode = que.front();que.pop();//记录左右子树的节点
TreeNode* rightNode = que.front();que.pop();
if(!leftNode && !rightNode){ //两个空节点,跳出当前while进入下一个while循环
continue;
}
if(!leftNode||!rightNode||(leftNode->val!=rightNode->val)) return false; //左节点右节点其中为空就不是,无空节点且左右值相等,不做处理,不相等就返回false
que.push(leftNode->left);//左左。右右,左右,右左
que.push(rightNode->right);
que.push(leftNode->right);
que.push(rightNode->left);
}
return true;
}
}; 543. 二叉树的直径
//直径就是求两个节点的一条边
class Solution{
public:
int result = 0;
int diameterOfBinaryTree(TreeNode* root){
if(root == NULL){
return 0;
}
dfs(root);
return result;
}
int dfs(TreeNode* root){
if(root==NULL) return 0; //也可以if(root->left == NULL && root->right == NULL)
int left = dfs(root->left);
int right = dfs(root->right);
//中间根节点的逻辑处理
if(root->left){//只需要判断左节点是否存在
left++;//根节点到左节点有一条边
}
else{
left = 0;
}
if(root->right){
right++;
}
else{
right = 0;
}
result = max(result,left+right);
return max(left,right);//返回根节点root 左右孩子的最大路径(边)==最大直径
//int left = dfs(2) ,此时根节点是2,返回的是4-2 还是5-2 的最大边 因为不可能4-2-5-1 连着只能4-2-1 一条边
}
};234. 回文链表
class Solution{
public:
bool isPalindrome(ListNode* head){
vector res;
while(head != NULL){
res.push_back(head->val);
head = head->next;
}
//放进数组容器,双指针
for(int i = 0,j = res.size()-1;i medium
53. 最大子数组和
class Solution {
public:
// 以i为尾下标的最大连续数组和 dp[i]
int maxSubArray(vector& nums) {
if(nums.size() <= 1) return nums[0];
vector dp(nums.size());
dp[0] = nums[0];
int result = dp[0]; // result 为一开始的数
for(int i = 1; i < nums.size();i++){
dp[i] = max(dp[i-1] + nums[i] ,nums[i]);//从前一个状态推,要么重新来过
if(result < dp[i]) result = dp[i];
}
return result;
}
}; hard
字典树题型
208. 实现 Trie (前缀树)
详解前缀树「TrieTree 汇总级别整理 」 - 实现 Trie (前缀树) - 力扣(LeetCode)
class Trie {
private:
bool isEnd;//尾部标识
Trie* next[26];//字典映射表
public:
Trie() {//默认初始化
isEnd = false;
memset(next,0,sizeof(next));//next默认初始化为0
}
void insert(string word) {
Trie* node = this;//当前节点
for(char c : word){
if(node->next[c-'a'] == nullptr){
node->next[c-'a'] = new Trie();
}
node = node->next[c-'a'];
}
node->isEnd = true;
}
bool search(string word) {
Trie* node = this;
for(char c : word){
node = node->next[c - 'a'];
if(node == NULL) return false;
}
return node->isEnd;
}
bool startsWith(string prefix) {
Trie* node = this;
for(char c : prefix){
node = node->next[c-'a'];
if(node == nullptr) return false;
}
return true;
}
};
/**
* Your Trie object will be instantiated and called as such:
* Trie* obj = new Trie();
* obj->insert(word);
* bool param_2 = obj->search(word);
* bool param_3 = obj->startsWith(prefix);
*/企业题型
华为
1、获取最多食物
主办方设计了一个获取食物的游戏。游戏的地图由N个方格组成,每个方格上至多2个传送门,通过传送门可将参与者传送至指定的其它方格。
同时,每个方格上标注了三个数字:
(1) 第一个数字id:代表方格的编号,从0到N-1,每个方格各不相同
(2)第二个数字parent-id:代表从编号为parent-id的方格可以通过传送门传送到当前方格(-1则表示没有任何方格可以通过传送门传送到此方格,这样的方格在地图中有且仅有一个);
(3)第不个数字value: 取值在[100,100]的整数值,正整数代表参与者得到相队取值单位的食物,负整数代表失去相应数值单位的食物(参与者可能存在临时持有食物为负数的情况),0则代表无变化。此外,地图设计时保证了参与者不可能到达相同的方格两次,并且至少有一个方格的value是正整数。
游戏开始后,参与者任意选择一个方格作为出发点,当遇到下列情况之一退出游戏:
(1)参与者当前所处的方格无传送门:
(2) 参与者在任意方格上丰动宣布退出游戏 请计算参与者退出游戏后,最多可以获得多少单位的食物
解答要求 时间限制: C/C++ 1300ms.其他语言:2600ms内存限制: C/C++256MB其他语言:512MB 第一行:方块个数N (N<10000)
输入:
7
0 1 8
1 -1 -2
2 1 9
4 0 -2
5 4 3
3 0 -3
6 2 -3
输出:
9
解释:
参与者从方格0出发,通过传送门到达方格4,再通过传送门到达方格5。一共获得8+(-2) +3=9个单位食物,得到食物展多: 或者参与者在游戏开始时处于方格2,直接主动宣布退出游戏,也可以获得9个单位食物。
输入:
3
0 -1 3
1 0 1
2 0 2
输出:
5
参与者从方格0出发,通过传送门到达方格2,一共可以获得3+2=5个单位食物,此时得到食物最多定义dp[i]表示以节点i结尾,可以获取的最大食物的数量。
对于dp[i],当前我们的选择有走到父节点和不走到父节点,我们取最大的即可。也就是
dp[i] = max(当前节点的食物, 当前节点的食物 + dp[parent_id])
我们需要把所有的dp[i]都枚举一次,最终复杂度为O(n)
#include
#include
#include
using namespace std;
int num;
vector dp;
vector> nodes;
int dfs(int id) {
if (dp[id] != INT_MIN) return dp[id];
if (nodes[id][0] == -1){
dp[i] = nodes[id][1];
return dp[i];//当前的 父节点为空,返回当前值
}
dp[id] = max(nodes[id][1], nodes[id][1] + dfs(nodes[id][0])); //max(当前食物,当前食物+深搜父节点的食物)
return dp[id];
}
int main() {
cin >> num;
nodes = vector>(num, vector(2));
for (int i = 0; i < num; i++) {
int id, pid, value;
cin >> id >> pid >> value;
nodes[id][0] = pid;
nodes[id][1] = value;
}
dp = vector(num, INT_MIN);
for (int i = 0; i < num; i++) {
dfs(i);
}
cout << *max_element(dp.begin(), dp.end()) << endl;
return 0;
} 2、交易系统的降级策略
有一个核心交易系统接口被N个上游系统调用,每个上游系统的调用量R=[R1,R2.....,RN].由于核心交易系统集群故障,需要暂时系统降级限制调用,核心交易系统能接受的最大调用量为cnt。
设置降级规则如下;如果sum(R1.R2..RN)小于等于cnt,则全部可以正常调用,返回-1;
如果sum(R1.R2....RN)大于cnt,设置一个闻值limil,如果某个上游系统发起的调用量超过limt,就将该上游系统的调用量限制为limit,其余未达到limit的系统可以正常发起调用。
求出这个最大的lmit (mit可以为0)此题目对效率有要求,请选择高效的方式。
解答要求
时间限制:C/C++ 1000ms,其他语言: 2000ms 内存限制:C/C++200MB其他语言:400MB
输入描述
第一行:每个上游系统的调用量(整型数组) 第二行:核心交易系统的最大调用量 0 输出描述 调用量的阈值Iimit 样例1输入: 输出: 解释: 样例2输入: 输出: 解释:因为即使imil设置为1,1+1+1+1+1+1+1+1=8>7也不满足,所以limit只能为0 服务器有三种运行状态:空载、单任务、多任务,每个时间片的能耗的分别为1、3、4; 每个任务由起始时间片和结束时间片定义运行时间: 如果一个时间片只有一个任务需要执行,则服务器处于单任务状态; 如果一个时间片有多个任务需要执行,则服务器处于多任务状态; 给定一个任务列表,请计算出从第一个任务开始,到所有任务结束,服务器的总能耗。 解答要求 时间限制: C/C++ 100ms,其他语言: 200ms 内存限制: C/C++ 128MB,其他语言: 256MB 输入 一个只包含整数的二维数组: 第一行的数字表示一共有多少个任务 后续每行包含由空格分割的两个整数,用于确定每一个任务的起始时间片和结束时间片; 任务执行时间包含起始和结束时间片,即任务执行时间是左闭右闭的; 结束时间片一定大于等于起始时间片; 时间片范围: [0,1000000]: 任务数范围: [1,10000]; 输出 一个整数,代表服务器的总能耗。 样例1 样例2 给定一棵树,这个树有n个节点,节点编号从0开始依次递增,0固定为根节点。在这棵树上有一个小猴子,初始时该猴子位于根节点(0号) 上,小猴子一次可以沿着树上的边从一个节点挪到另一个节点,但这棵树上有一些节点设置有障碍物,如果某个节点上设置了障碍物,小猴子就不能通过连接该节点的边挪动到该节点上。问小猴子是否能跑到树的叶子节点(叶子节点定义为只有一条边连接的节点),如果可以,请输出小猴子跑到叶子节点的最短路径(通过的边最少),否则输出字符串NULL。 解答要求 时间限制: C/C++ 1000ms,其他语言: 2000ms 内存限制: C/C++ 256MB,其他语言: 512MB 输入 第一行给出数字n,表示这个树有n个节点,节点编号从0开始依次递增,0固定为根节点,1<=n<10000 第二行给出数字edge,表示接下来有edge行,每行是一条边 接下来的edge行是边: x y,表示x和y节点有一条边连接 边信息结束后接下来的一行给出数字block,表示接下来有block行,每行是个障碍物 接下来的block行是障碍物: X,表示节点x上存在障碍物 输出 如果小猴子能跑到树的叶子节点,请输出小猴子跑到叶子节点的最短路径(通过的边最少),比如小猴子从0经过1到达2 (叶子节点) ,那么输出“0->1->2”,否则输出“NULL”。注意如果存在多条最短路径,请按照节点序号排序输出,比如0->1和0->3两条路径,第一个节点0一样,则比较第二个节点1和3,1比3小,因此输出0->1这条路径。再如 0->5->2->3 和0->5->1->4,则输出 0->5-31->4 样例1 样例2 样例3 样例4 在雷火的某款大型游戏中有一种具有无人机攻击功能的环形基地,基地呈圆环形,圆环上最初有C台无人机,无人机初始为可派遣状态。 记当前基地的无人机总数为C, 玩家可以有两种请求: 1.派遣m台无人机 (1)当m > C时,如果剩余可派遣无人机数量n = C,也就是此时没有无人机被派遣出去,则可将基地进行升级,无人机数量会变成m,并立马可以将所有无人机派遣出去,成功完成本次派遣,否则派遣失败。 (2)当m <= C时,如果剩余可派遣无人机数量n< m,则派遣失败;如果n >=m,则成功派遣m台无人机。 (3)失败的派遣请求会先存储到等待队列的队尾,等待下一次派遣。 2.返回前面某一批次的无人机 (1)收到返回通知时,无人机将返回环形基地,并进入休眠状态。当所有更早被成功派遣出去的无人机都返回基地之后(注意: 更早 是指实际派遣顺序的更早,而不是派遣ID),处于休眠状态的无人机才能重新进入可派遣状态。 (2)返回操作完成后,会重新对等待队列中的请求进行派遣,直到遇到第一个失败的派遣,该失败的派遣请求会继续留在等待队列的头部。 对于按时序给出的一系列派遣和返回请求,给出每次请求结去的无人机的数量。 输入描述 第一行,输入一个整数c (0 接下来的N行,每行输入两个整数a和b,相互之间由空格隔开。如果>= 0,则代表这是一个派遣请求,且a为派遣请求的id; 如果a =-1,是一个返回请求。对于派遣请求,第二个整数b代表请求派遣的无人机数0);对于返回请求上第二个整数b代表返回的派遣请求的id。 注:不会有无效的返回请求,即返回请求给出时,对应的派遣请求必派遣。 输出描述 n行整数,表示每次请求之后,新派遣出去的无人机数量 样例 样例一 输入 输出 样例二 输入 输出1 4 2 5 5 1 6
13 2因为1+4+2+5+5+1+6>13;将limit设置为2,则1+2+2+2+2+1+2=12<13。所以imit为21 7 8 8 1 0 2 4 9
70#include4.19
1、服务器能耗统计
1. num
2. start0 end0
3. start1 end1
4. ...输入:
2
2 5
8 9
输出: 20
解释: [01] 没有任务需要执行,能耗为0[2.5]处于单任务状态,能耗为3*4 = 12[6,7] 处于空载状态,能耗为1*2 = 2[8,9]处于单任务状态,能耗为3*2 =6共计能耗为12 + 2 + 6 = 20输入:
3
4 8
1 6
2 9
输出:
34
解释:[1,1] 处于单任务状态,能耗为3*1= 3[2,8] 处于多任务状态,能耗为4*7=28[9,9]处于单任务状态,能耗为3*1 = 3共计能耗为3 + 28 + 3 = 34#include2、树上逃离
输入:
4
3
0 1
0 2
0 3
2
2
3
输出:
0->1
解释: n=4,edge=[[0,1],[0,2],[0,3]],block=[2,3]表示一个有4个节点、3条边的树,其中节点2和节点3上有障碍物,小猴子能从0到达叶子节点1 (节点1只有一条边[1,0]和它连接,因此是叶子节点) ,即可以跑出这个树,所以输出为0->1。输入:
7
6
0 1
0 3
1 2
3 4
1 5
5 6
1
输出:
0->1->2
解释: 节点4上有障碍物,因此0-3-4这条路不通,节点2和节点6都是叶子节点,但0->1->2比0->1->5->6路径短(通过的边最少) ,因此输出为0->1->2输入:
2
1
0 1
1
1
输出:
NULL
解释:节点1是叶子节点,但存在障碍物,因此小猴子无法到达叶子节点,输出NULL输入:
4
3
0 1
0 2
0 3
1
2
输出:
0->1
解释: n=4,edge=[[0,1],[0,2],[0,3]],block=[2] 表示一个有4个节点、3条边的树,其中节点2上有障碍物,小猴子能从0到达叶子节点1 (节点1只有一条边[0,1]和它连接,因此是叶子节点) ,路径是0->1,也能从0到达叶子节点3(节点3只有一条边[0,3]和它连接,因此是叶子节点) ,路径是0->3,因此按通过节点的顺序及序号比较选择 0->1。#include拼多多
#include 网易
3 5
0 2
1 2
-1 0
2 4
-1 12
0
2
0
410 9
0 3
1 2
2 4
-1 0
-1 2
3 2
4 3
-1 1
5 53
2
4
0
0
2
0
3
5#include