【算法与数据结构】98、LeetCode验证二叉搜索树
文章目录
- 一、题目
- 二、解法
- 三、完整代码
所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。
一、题目
二、解法
思路分析:注意不要落入下面你的陷阱,笔者本来想左节点键值<中间节点键值<右节点键值即可,写出如下代码:
class Solution2 {
public:
// 1、输入参数, 返回值为result,以引用方式传入
void traversal_preOrder(TreeNode* cur, bool &result) {
// 2、终止条件
if (cur == NULL) return;
if (cur->left && cur->left->val >= cur->val) result = 0;
if (cur->right && cur->right->val <= cur->val) result = 0;
// 3、单层递归逻辑
if (result) traversal_preOrder(cur->left, result); // 左
if (result) traversal_preOrder(cur->right, result); // 右
}
bool isValidBST(TreeNode* root) {
bool result = 1;
traversal_preOrder(root, result);
return result;
}
};
在leetcode执行时遇到下面的错误,再次读题,发现是所有左子树的键值小于中间节点键值,所有右子树键值大于中间节点键值,这个性质和中序遍历有所关联。如此一来,我们就想到用中序遍历来做,中序遍历数组是一个有序数组,判断该数组是否有序即可。
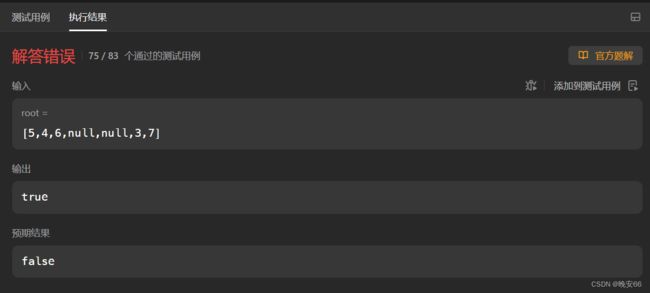
程序如下:
class Solution {
public:
void traversal_midOrder(TreeNode* cur, vector<int>& vec) {
if (cur == NULL) return;
traversal_midOrder(cur->left, vec); // 左
vec.push_back(cur->val); // 中
traversal_midOrder(cur->right, vec); // 右
}
bool isValidBST(TreeNode* root) {
if (root == NULL) return {};
vector<int> v;
traversal_midOrder(root, v);
for (int i = 0; i < v.size()-1; i++) {
if (v[i] >= v[i + 1]) return false;
}
return true;
}
};
三、完整代码
# include end

