HDU4453--Looploop (Splay伸展树)

Looploop

XXX gets a new toy named Looploop. The toy has N elements arranged in a loop, an arrow pointing to one of the elements, and two preset parameters k1 and k2. Every element has a number on it.

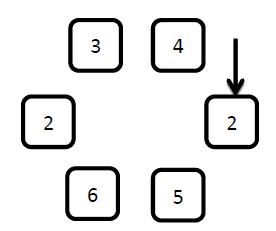
The figure above shows a Looploop of 6 elments. Let's assuming the preset parameter k1 is 3, and k2 is 4.
XXX can do six operations with the toy. 

1: add x 
Starting from the arrow pointed element, add x to the number on the clockwise first k2 elements.

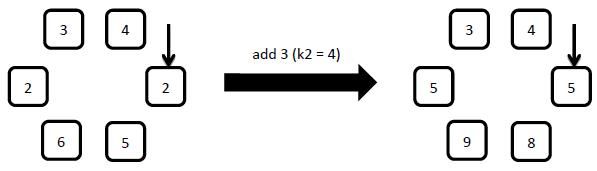
2: reverse
Starting from the arrow pointed element, reverse the first k1 clockwise elements.

3: insert x 
Insert a new element with number x to the right (along clockwise) of the arrow pointed element.

4: delete 
Delete the element the arrow pointed and then move the arrow to the right element.

5: move x 
x can only be 1 or 2. If x = 1 , move the arrow to the left(along the counterclockwise) element, if x = 2 move the arrow to the right element.

6: query
Output the number on the arrow pointed element in one line.

XXX wants to give answers to every query in a serial of operations.

 

 

Input

There are multiple test cases.
For each test case the first line contains N,M,k1,k2(2≤k1<k2≤N≤10 ⁵, M≤10 ⁵) indicating the initial number of elements, the total number of operations XXX will do and the two preset parameters of the toy. 
Second line contains N integers ai(-10 ⁴≤ai≤10 ⁴) representing the N numbers on the elements in Looploop along clockwise direction. The arrow points to first element in input at the beginning. 
Then m lines follow, each line contains one of the six operations described above.
It is guaranteed that the "x" in the "add","insert" and "move" operations is always integer and its absolute value ≤104. The number of elements will never be less than N during the operations. 
The input ends with a line of 0 0 0 0.

Output

For each test case, output case number in the first line(formatted as the sample output). Then for each query in the case, output the number on the arrow pointed element in a single line.

 

Sample Input

5 1 2 4 3 4 5 6 7 query 5 13 2 4 1 2 3 4 5 move 2 query insert 8 reverse query add 2 query move 1 query move 1 query delete query 0 0 0 0

 

Sample Output

Case #1:

3

Case #2:

2

8

10

1

5

1

2012 Asia Hangzhou Regional Contest

题意很简单，就像题目中 图片中描述的一样。Splay大法好啊。

  1 #include <cstdio>

  2 #include <cstdlib>

  3 #include <cstring>

  4 #include <algorithm>

  5 using namespace std;

  6 const int inf = 0x3f3f3f3f;

  7 const int maxn = 100086;

  8 int pre[maxn],ch[maxn][2],key[maxn],addv[maxn],rev[maxn],siz[maxn];

  9 int tot1,tot2,root,s[maxn];  //s为内存池

 10 int a[maxn],n,m,k1,k2;

 11 void update_add(int r,int val)

 12 {

 13     if (!r)

 14         return;

 15     key[r] += val;

 16     addv[r] += val;

 17 }

 18 void update_rev(int r)

 19 {

 20     if (!r)

 21         return;

 22     swap(ch[r][0],ch[r][1]);

 23     rev[r] ^= 1;

 24 }

 25 void push_down(int r)

 26 {

 27     if (rev[r])

 28     {

 29         update_rev(ch[r][0]);

 30         update_rev(ch[r][1]);

 31         rev[r] = 0;

 32     }

 33     if (addv[r])

 34     {

 35         update_add(ch[r][0],addv[r]);

 36         update_add(ch[r][1],addv[r]);

 37         addv[r] = 0;

 38     }

 39 }

 40 void push_up(int r)

 41 {

 42     siz[r] = siz[ch[r][0]] + siz[ch[r][1]] + 1;

 43 }

 44 void NewNode (int &r,int father,int k)

 45 {

 46     if (tot2)

 47         r = s[tot2--];

 48     else

 49         r = ++tot1;

 50     pre[r] = father;

 51     siz[r] = 1;

 52     rev[r] = 0;

 53     addv[r] = 0;

 54     ch[r][0] = ch[r][1] = 0;

 55     key[r] = k;

 56 }

 57 void build(int &x,int l,int r,int father)

 58 {

 59     if (l > r)

 60         return ;

 61     int mid = (l + r) >> 1;

 62     NewNode(x,father,a[mid]);

 63     build(ch[x][0],l,mid-1,x);

 64     build(ch[x][1],mid+1,r,x);

 65     push_up(x);

 66 }

 67 void init()

 68 {

 69     tot1 = tot2 = root = 0;

 70     for (int i = 1; i <= n; i++)

 71         scanf ("%d",a+i);

 72     NewNode(root,0,inf);

 73     NewNode(ch[root][1],root,inf);

 74     build(ch[ch[root][1]][0],1,n,ch[root][1]);

 75     push_up(root);

 76     push_up(ch[root][1]);

 77 }

 78 void Rotate(int r,int kind)

 79 {

 80     int y = pre[r];

 81     push_down(y);

 82     push_down(r);

 83     ch[y][!kind] = ch[r][kind];

 84     pre[ch[r][kind]] = y;

 85     if (pre[y])

 86         ch[pre[y]][ch[pre[y]][1] == y] = r;

 87     ch[r][kind] = y;

 88     pre[r] = pre[y];

 89     pre[y] = r;

 90     push_up(y);

 91 }

 92 

 93 void Splay(int r,int goal)

 94 {

 95     push_down(r);

 96     while (pre[r] != goal)

 97     {

 98         if (pre[pre[r]] == goal)

 99         {

100             push_down(pre[r]);

101             push_down(r);

102             Rotate(r,ch[pre[r]][0] == r);

103         }

104         else

105         {

106             int y = pre[r];

107             int kind = (ch[pre[y]][1] == y);

108             push_down(pre[y]);

109             push_down(y);

110             push_down(r);

111             if (ch[y][kind] == r)

112             {

113                 Rotate(y,!kind);

114                 Rotate(r,!kind);

115             }

116             else

117             {

118                 Rotate(r,kind);

119                 Rotate(r,!kind);

120             }

121         }

122     }

123     push_up(r);

124     if (goal == 0)

125         root = r;

126 }

127 int Get_kth(int r,int k)

128 {

129     push_down(r);

130     int t = siz[ch[r][0]] + 1;

131     if (t == k)

132         return r;

133     if (t > k)

134         return Get_kth(ch[r][0],k);

135     else

136         return Get_kth(ch[r][1],k-t);

137 }

138 void ADD(int x)

139 {

140     Splay (Get_kth(root,1),0);

141     Splay(Get_kth(root,k2+2),root);

142     update_add(ch[ch[root][1]][0],x);

143     push_up(ch[root][1]);

144     push_up(root);

145 }

146 void Reverse(int u,int v)

147 {

148     Splay(Get_kth(root,u),0);

149     Splay(Get_kth(root,v+2),root);

150     update_rev(ch[ch[root][1]][0]);

151     push_up(ch[root][1]);

152     push_up(root);

153 }

154 void Insert(int x)

155 {

156     Splay(Get_kth(root,2),0);

157     Splay(Get_kth(root,3),root);

158     NewNode(ch[ch[root][1]][0],ch[root][1],x);

159     push_up(ch[root][1]);

160     push_up(root);

161 }

162 void eraser(int r)

163 {

164     if (!r)

165         return;

166     s[++tot2] = r;

167     eraser(ch[r][0]);

168     eraser(ch[r][1]);

169 }

170 void Delete()

171 {

172     Splay(Get_kth(root,1),0);

173     Splay(Get_kth(root,3),root);

174     eraser(ch[ch[root][1]][0]);

175     pre[ch[ch[root][1]][0]] = 0;

176     ch[ch[root][1]][0] = 0;

177     push_up(ch[root][1]);

178     push_up(root);

179 }

180 void Move(int x)               //Move操作就是两个 区间reverse操作。

181 {

182     if (x == 1)

183     {

184         Reverse(1,n);

185         Reverse(2,n);

186     }

187     if (x == 2)

188     {

189         Reverse(1,n);

190         Reverse(1,n-1);

191     }

192 }

193 int query()

194 {

195     Splay(Get_kth(root,1),0);

196     Splay(Get_kth(root,3),root);

197     return key[ch[ch[root][1]][0]];

198 }

199 int main(void)

200 {

201     #ifndef ONLINE_JUDGE

202         freopen("in.txt","r",stdin);

203     #endif

204     int cas = 1;

205     while (~scanf ("%d%d%d%d",&n,&m,&k1,&k2))

206     {

207         if (n == 0 && m == 0 && k1 == 0 && k2 == 0)

208             break;

209         printf("Case #%d:\n",cas++);

210         init();

211         for (int i = 0; i < m; i++)

212         {

213             char op[8];

214             int x;

215             scanf ("%s",op);

216             if (op[0] == 'a')

217             {

218                 scanf ("%d",&x);

219                 ADD(x);

220             }

221             if (op[0] == 'r')

222                 Reverse(1,k1);

223             if (op[0] == 'i')

224             {

225                 scanf ("%d",&x);

226                 Insert(x);

227                 n++;           // insert一个数  n自然加1

228             }

229             if (op[0] == 'd')

230             {

231                 Delete();

232                 n--;          //delete一个数 n减1

233             }

234             if (op[0] == 'm')

235             {

236                 scanf ("%d",&x);

237                 Move(x);

238             }

239             if (op[0] == 'q')

240                 printf("%d\n",query());

241         }

242     }

243     return 0;

244 }