Day 45 | 70. 进阶爬楼梯 & 322. 零钱兑换 & 279.完全平方数

 70. 进阶爬楼梯

完全背包解题思路： 

爬楼梯原题目是一次只能爬1/2层台阶，若改为一次可以爬m个台阶，即为完全背包的排列问题。

每次可以跳[1,i]，跳到第j阶，共有dp[j]种方法

递推公式：dp[j]+=dp[j-nums[i]]

因为是排列问题，因此先遍历容量（跳1/2层台阶），再遍历背包（跳到了多少层台阶）。容量从前往后计算。

    public int combinationSum4(int[] nums, int target) {
        int[] dp=new int[target+1];
        dp[0]=1;
        for(int j=0;j<=target;j++){
            for(int i=0;i=0){
                    dp[j]+=dp[j-nums[i]];
                    }
            }
        }
        return dp[target];
    }

322. 零钱兑换 

完全背包解题思路：

        硬币无限个，凑成总金额（装满背包）：完全背包问题。

        本题求的是最少硬币个数，可转换为[0,i[个硬币，凑成金额j，所需钱币最少为dp[j]

每次遍历时有两种选择：

①取：dp[j]=dp[j-nums[i]+1  (凑成金额为j-nums[i[所需的最少硬币再加1即为凑成j的最少硬币数)

②不取，dp[j]=dp[j]

因为求的是最少硬币数，每次对这两个数取小即可。

因此，状态转移方程为：dp[j]=Math.min(dp[j],dp[j-nums[i]]+1);

数组的初始化

        所有dp[j]都先定义为为最大值。dp[0]=0,当金额为0时要0个硬币。

数组的遍历顺序

        完全背包问题，本题是要求最少硬币数量，硬币是组合数还是排列数都无所谓！所以两个for循环先后顺序怎样都可以。但是遍历容量要从前向后遍历，满足一个硬币可放多次的条件。

        int max=Integer.MAX_VALUE;
        int[] dp=new int[amount+1];
        for(int j=0;j<=amount;j++){
            dp[j]=max;
        }
        dp[0]=0;
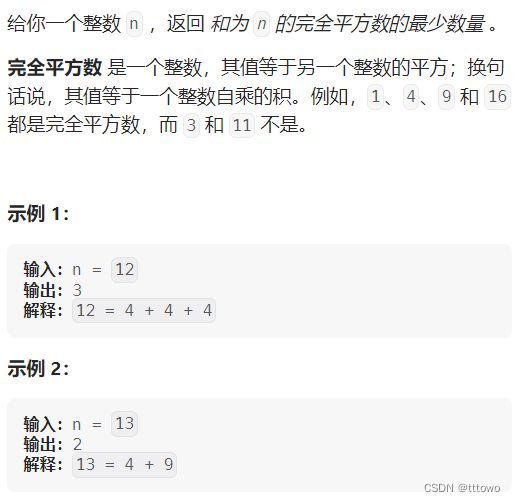
        for(int i=0;i

279. 完全平方数

完全背包解题思路：

        每个物品为i*i（平方数），物品有无限个，凑成和为j，最小有dp[j]个完全平方数。

①确定dp数组以及下标含义

        dp[j]：每个物品大小为i*i,装满容量j的背包，最少个数为dp[j]个。

②确定递推公式

        遇上题相同，求的是最小个数。

取的时候为装满容量j-i*i的最少个数+1（当前这个数）；不取即为dp[j]

                                        dp[j]=Math.min(dp[j],dp[j]-i*i]+1); 

③dp数组如何初始化

      所有dp[j]都先定义为为最大值。dp[0]=0,

④确定遍历顺序

        与上一题相同。

        本题是要求最少平方数的个数，是组合数还是排列数都无所谓！所以两个for循环先后顺序怎样都可以。但是遍历容量要从前向后遍历，满足一个数可放多次的条件。

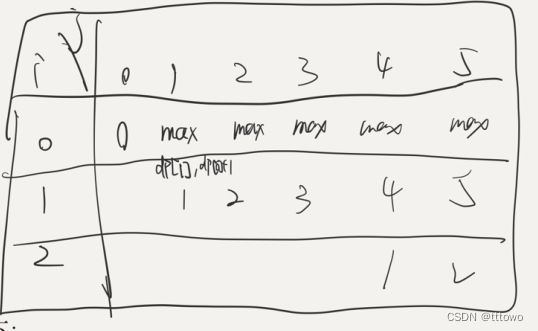
⑤举例推导dp数组

   n=5 ：

    public int numSquares(int n) {
        int[] dp = new int[n + 1];
        int max = Integer.MAX_VALUE;
        for (int j = 0; j <= n; j++) {
            dp[j] = max;
        }
        dp[0] = 0;
        for (int i = 1; i * i <= n; i++) {
            for (int j = i * i; j <= n; j++) {
                if (dp[j - i * i] != max) {
                    dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
                }
            }
        }
        return dp[n];

    }