代码随想录 - Day35 - 回溯:重新安排行程,棋盘问题
代码随想录 - Day35 - 回溯:重新安排行程,棋盘问题
332. 重新安排行程
输入:tickets = [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
输出:["JFK","ATL","JFK","SFO","ATL","SFO"]
解释:另一种有效的行程是 ["JFK","SFO","ATL","JFK","ATL","SFO"] ,但是它字典排序更大更靠后。
取[JFK,SFO]
取[JFK,ATL]
取[SFO,ATL]
取[ATL,JFK]
取[ATL,SFO]
取[ATL,JFK]
取[ATL,SFO]
取[JFK,SFO]
取[SFO,ATL]
取[JFK,ATL]
取[SFO,ATL]
取[ATL,JFK]
取[ATL,SFO]
取[ATL,SFO]
取[JFK,SFO]
[JFK,ATL,JFK,SFO,ATL,SFO] < [JFK,ATL,SFO,ATL,JFK,SFO] < [JFK,SFO,ATL,JFK,ATL,SFO]
[JFK,ATL,JFK,SFO,ATL,SFO]
[JFK,SFO,ATL]
[JFK,ATL,JFK]
[JFK,ATL,SFO]
[JFK,SFO,ATL,JFK]
[JFK,SFO,ATL,SFO]
[JFK,SFO,JFK,SFO]
[JFK,ATL,SFO,ATL]
[JFK,SFO,ATL,JFK,ATL]
[JFK,ATL,JFK,SFO,ATL]
[JFK,ATL,SFO,ATL,JFK]
即[JFK,SFO,ATL,JFK,ATL,SFO]
[JFK,ATL,SFO,ATL,JFK,SFO]
最终答案:行程有效 + 按字典排序最小
行程有效:
- 第一个必须从
JFK出发 - 所有机票必须且只能用一次
class Solution:
def backtracking(self, tickets, used, path, cur, result):
if len(path) == len(tickets) + 1: # 有效行程比票数大1,所以判断条件应该写成这样
result.append(path[:])
return True
for i, ticket in enumerate(tickets):
if ticket[0] == cur and used[i] == False: # 没用过的机票 + 出发机场和上一次的到达机场必须是同一个
used[i] = True # 用过的机票设为True
path.append(ticket[1]) # 只向path中添加到达机场
state = self.backtracking(tickets, used, path, ticket[1], result)
path.pop() # 回溯,pop
used[i] = False # 回溯,把机票设回False
if state: # 只要找到一个可行路径就返回,不继续搜索
return True
def findItinerary(self, tickets: List[List[str]]) -> List[str]:
result = []
tickets.sort() # 提前给tickets排序,这样收集到result时的顺序一定是字典序由小到大的
path = ["JFK"] # 第一个从JFK出发
used = [False] * len(tickets) # 没用过的tickets设为False
self.backtracking(tickets, used, path, "JFK", result)
return result[0]
上述代码也可以写成这样:
class Solution:
def backtracking(self, tickets, used, path, cur, result):
if len(path) == len(tickets) + 1:
result.append(path[:])
return True
for i in range(len(tickets)):
if tickets[i][0] == cur and used[i] == False:
used[i] = True
path.append(tickets[i][1])
state = self.backtracking(tickets, used, path, tickets[i][1], result)
path.pop()
used[i] = False
if state:
return True
def findItinerary(self, tickets: List[List[str]]) -> List[str]:
result = []
tickets.sort()
path = ["JFK"]
used = [False] * len(tickets)
self.backtracking(tickets, used, path, "JFK", result)
return result[0]
使用字典:比上面的代码复杂了一点,但是速度更快
defaultdict()中只能存在不同的 key。
- 添加元素时(
[key1, value2]),如果defaultdict()里面已经有一个key1了({key1: value1}) ,就不会新建一个key1,而是把value2添加在key1原本的value1后面({key1: [value1, value2]})
from collections import defaultdict
class Solution:
def backtracking(self, targets, path, ticketNum):
if len(path) == ticketNum + 1:
return True # 找到有效行程
airport = path[-1] # 当前机场(path中最后一个元素)
destinations = targets[airport] # 取机场字典中的当前机场对应的 value 值,即为当前机场可以到达的机场列表
for i, dest in enumerate(destinations):
targets[airport].pop(i) # 标记已使用的机票(把第 i 张机票删掉)
# pop掉的i对应的到达机场 == path.append()的dest表示的到达机场
path.append(dest) # 添加目的地到路径
if self.backtracking(targets, path, ticketNum):
return True # 找到有效行程
targets[airport].insert(i, dest) # 回溯,恢复机票(把第 i 张机票插入回 i 的位置
path.pop() # 移除目的地
return False # 没有找到有效行程
def findItinerary(self, tickets: List[List[str]]) -> List[str]:
targets = defaultdict(list) # 构建机场字典
# 把出发机场作为 key,到达机场作为 value
# 如 JFK : SFO, ATL
for ticket in tickets:
targets[ticket[0]].append(ticket[1])
# 对到达机场列表进行排序
# 如 JFK : SFO, ATL 排序为 JFK : ATL, SFO
for airport in targets:
targets[airport].sort()
path = ["JFK"] # 起始机场为"JFK"
self.backtracking(targets, path, len(tickets))
return path
这道题是困难题,但是,把图画出来之后觉得不是很难,思路也比较好想,就是代码不好写。
敲代码能力有很大的进步空间。
可能是因为敲的太少手生吧。
51. N皇后
将 n 个皇后放置在 n × n 的棋盘上,并且使皇后彼此之间不能相互攻击,即这 n 个皇后不能处于同一行 / 同一列 / 同一斜线。
给一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表皇后和空位。
假设Q占据的格子为 [x, y] ,那么 [x1~xn, y],[x, y1~yn],[x+i, y+i],[x-i, y-i],都不能再放其它Q了。要注意边界范围,所有的坐标都小于n。
class Solution:
def isValid(self, row, col, chessBoard):
# 检查列
for i in range(row):
if chessBoard[i][col] == "Q":
return False
# 检查 45 度角是否有皇后
i, j = row - 1, col - 1
while i >= 0 and j >= 0:
if chessBoard[i][j] == "Q":
return False # 左上方向已经存在皇后,不合法
i -= 1
j -= 1
# 检查 135 度角是否有皇后
i, j = row - 1, col + 1
while i >= 0 and j < len(chessBoard):
if chessBoard[i][j] == "Q":
return False # 右上方向已经存在皇后,不合法
i -= 1
j += 1
return True
def backtracking(self, n, row, chessBoard, result):
if row == n:
result.append(chessBoard[:]) # 棋盘填满,将当前解加入结果集
return
for col in range(n):
if self.isValid(row, col, chessBoard):
chessBoard[row] = chessBoard[row][:col] + 'Q' + chessBoard[row][col+1:] # 放置皇后
self.backtracking(n, row + 1, chessBoard, result) # 递归到下一行
chessBoard[row] = chessBoard[row][:col] + '.' + chessBoard[row][col+1:] # 回溯,撤销当前位置的皇后
def solveNQueens(self, n: int) -> List[List[str]]:
result = []
chessBoard = ['.' * n for _ in range(n)] # 初始化棋盘
self.backtracking(n, 0, chessBoard, result)
return [[''.join(row) for row in solution] for solution in result] # 变成字符串放进 list 返回
我想不通,明明我的思路没错,为什么代码总是报错!
找到问题了,因为字符串不能直接修改,所以只好用切片的方式修改,这样才能正常运行,并得到正确结果。
37. 解数独
这道题不让return,只能在原有board里修改
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
数独部分空格内已填入了数字,空白格用 '.' 表示。
数独只有一个解
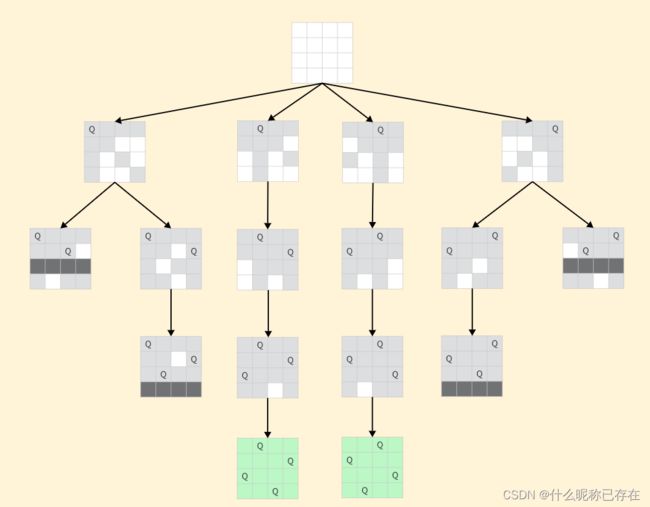
借用代码随想录里面的图:

本题中棋盘的每一个位置都要放一个数字(而N皇后是一行只放一个皇后),并检查数字是否合法,解数独的树形结构要比N皇后更宽更深。
本题递归不用终止条件,解数独是要遍历整个树形结构寻找可能的叶子节点就立刻返回。
不用终止条件不会死循环
递归的下一层的棋盘一定比上一层的棋盘多一个数,等数填满了棋盘自然就终止(填满当然好了,说明找到结果了),所以不需要终止条件!
递归逻辑:
一个for循环遍历棋盘的行,一个for循环遍历棋盘的列,一行一列确定下来之后,递归遍历这个位置放9个数字的可能性!
class Solution:
def isValid(self, row, col, val, board):
for i in range(9):
if board[row][i] == str(val):
return False
for j in range(9):
if board[j][col] == str(val):
return False
startRow = (row // 3) * 3
startCol = (col // 3) * 3
for i in range(startRow, startRow + 3):
for j in range(startCol, startCol + 3):
if board[i][j] == str(val):
return False
return True
def backtracking(self, board):
for i in range(len(board)):
for j in range(len(board[0])):
if board[i][j] != ".":
continue
for k in range(1, 10):
k = str(k)
if self.isValid(i, j, k, board):
board[i][j] = k
if self.backtracking(board):
return True
board[i][j] = '.'
return False
return True
def solveSudoku(self, board: List[List[str]]) -> None:
"""
Do not return anything, modify board in-place instead.
"""
self.backtracking(board)
今天这三道题让我感到恶心