AcWing算法基础课第一讲(2):高精度加减乘除、前缀和、差分

1. 高精度加法

这里讲解两个大整数的加法运算，比如给定两个整数A、B，且A和B的长度len(A)、len(B) ≤ 10⁶。此时如果想将这两个大整数相加，就需要对大整数进行存储，我们这里选用vector数组分别存储A、B，高精度加法如下：

注：用t来表示上一位的进位;

高精度加法模版

// C = A + B, A >= 0, B >= 0
vector<int> add(vector<int> &A, vector<int> &B)
{
    if (A.size() < B.size()) return add(B, A); // 确保len(A) ≥ len(B)
    
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i ++ )
    {
        t += A[i];
        if (i < B.size()) t += B[i];
        C.push_back(t % 10); //将A+B+t的个位添加到C中
        t /= 10; //将t更新为该位的进位
    }

    if (t) C.push_back(t); // 如果最后还存在进位，就将t添加到C中
    return C;
}

模板题 AcWing 791. 高精度加法
给定两个正整数（不含前导 0），计算它们的和。
输入格式
共两行，每行包含一个整数。
输出格式
共一行，包含所求的和。
数据范围
1≤整数长度≤100000
输入样例：
12
23
输出样例：
35

#include 
#include 

using namespace std;

vector<int> add(vector<int> &A, vector<int> &B) {
    if (A.size() < B.size()) return add(B, A);
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i++) {
        t += A[i];
        if (i <= B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }
    if (t) C.push_back(t);
    return C;
}

int main() {
    string a, b;
    cin >> a >> b;
    vector<int> A, B;
    //先将a的个位存放在A[0],原因是加法的结果可能存在进位，这样存放可将最高位存储在A的最后边，便于对数组的操作
    for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0'); 
    for (int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');
    
    auto C = add(A, B);
    //由于将结果的最高位存储在C的最后一位，所以将结果输出时，从i=C.size()-1输出C[i]
    for (int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
    return 0;
}

2. 高精度减法

这里讲解两个大整数的减法运算，比如给定两个整数A、B，且A和B的长度len(A)、len(B) ≤ 10⁶。此时如果想将这两个大整数相减，就需要对大整数进行存储，我们这里选用vector数组分别存储A、B，高精度减法如下：

注：用t来表示上一位的借位;

高精度减法模版

// C = A - B, 满足A >= B, A >= 0, B >= 0
vector<int> sub(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    for (int i = 0, t = 0; i < A.size(); i ++ )
    {
        t = A[i] - t;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if (t < 0) t = 1;
        else t = 0;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

模板题 AcWing 792. 高精度减法
给定两个正整数（不含前导 0），计算它们的差，计算结果可能为负数。
输入格式
共两行，每行包含一个整数。
输出格式
共一行，包含所求的差。
数据范围
1≤整数长度≤100000
输入样例：
32
11
输出样例：
21

#include 
#include 
using namespace std;

vector<int> sub(vector<int> &A, vector<int> &B) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i++) {
        t = A[i] - t;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if (t < 0) t = 1;
        else t = 0;
    }
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}
// cmp函数用于比较A和B的大小，若A ≥ B，返回true；否则，返回false
bool cmp(vector<int> &A, vector<int> &B) {
    if (A.size() != B.size()) return A.size() > B.size();
    for (int i = A.size() - 1; i >= 0; i--) {
        if (A[i] != B[i]) return A[i] > B[i];
    }
    return true;
}

int main() {
    string a, b;
    cin >> a >> b;
    vector<int> A, B;
    for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
    for (int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');
    
    vector<int> C;
    if (cmp(A, B)) C = sub(A, B);
    else C = sub(B, A), cout << "-";
    
    for (int i = C.size() - 1; i >= 0; i--) cout << C[i];
    cout << endl;
    return 0;
}

3. 高精度乘低精度

这里讲解一个大整数A和一个小整数b的乘法运算，A的长度len(A) ≤ 10⁶。此时需要对大整数进行存储，我们这里选用vector数组存储A，高精度乘低精度如下：

注：用t来表示上一位的进位;

高精度乘低精度模版

// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> &A, int b)
{
    vector<int> C;

    int t = 0;
    for (int i = 0; i < A.size() || t; i ++ )
    {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

模板题 AcWing 793. 高精度乘低精度
给定两个非负整数（不含前导 0） A 和 B，请你计算 A×B 的值。
输入格式
共两行，第一行包含整数 A，第二行包含整数 B。
输出格式
共一行，包含 A×B 的值。
数据范围
1≤A的长度≤100000,
0≤B≤10000
输入样例：
2
3
输出样例：
6

#include 
#include 

using namespace std;

vector<int> mul(vector<int> &A, int b) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i++) {
        t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }
    while (t) {
        C.push_back(t % 10);
        t /= 10;
    }
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main() {
    string a;
    int b;
    cin >> a >> b;
    vector<int> A;
    for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
    auto C = mul(A, b);
    for (int i = C.size() - 1; i >= 0; i--) printf("%d", C[i]);
    return 0;
}

4. 高精度除以低精度

这里讲解一个大整数A和一个小整数b的除法运算，A的长度len(A) ≤ 10⁶。此时需要对大整数进行存储，我们这里选用vector数组存储A，高精度除以低精度如下：

注：用r来表示上一位的余数，并将r初始化为0;

高精度除以低精度模版

// A / b = C ... r, A >= 0, b > 0
vector<int> div(vector<int> &A, int b, int &r)
{
    vector<int> C;
    r = 0;
    //注意除法运算时A的遍历顺序
    for (int i = A.size() - 1; i >= 0; i -- )
    {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

模板题 AcWing 794. 高精度除以低精度
给定两个非负整数（不含前导 0） A，B，请你计算 A/B 的商和余数。
输入格式
共两行，第一行包含整数 A，第二行包含整数 B。
输出格式
共两行，第一行输出所求的商，第二行输出所求余数。
数据范围
1≤A的长度≤100000,
1≤B≤10000,
B 一定不为 0
输入样例：
7
2
输出样例：
3
1

#include 
#include 
#include 
using namespace std;

vector<int> div(vector<int> &A, int b, int &r) {
    vector<int> C;
    r = 0;
    for (int i = A.size() - 1; i >= 0; i--) {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main() {
    string a;
    int b, r;
    cin >> a >> b;
    vector<int> A;
    for (int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
    
    auto C = div(A, b, r);
    
    for (int i = C.size() - 1; i >= 0; i--) cout << C[i];
    cout << endl;
    cout << r << endl;
    return 0;
}

5. 一维前缀和

已知一个数组a，通过数组a的前缀和可得到a中任意区间和：

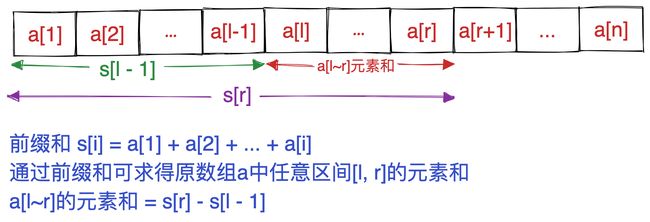
注：原数组a的下标从1开始存储

一维前缀和模版

S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]

模板题 AcWing 795. 前缀和
输入一个长度为 n 的整数序列。
接下来再输入 m 个询问，每个询问输入一对 l,r。
对于每个询问，输出原序列中从第 l 个数到第 r 个数的和。
输入格式
第一行包含两个整数 n 和 m。
第二行包含 n 个整数，表示整数数列。
接下来 m 行，每行包含两个整数 l 和 r，表示一个询问的区间范围。
输出格式
共 m 行，每行输出一个询问的结果。
数据范围
1≤l≤r≤n,
1≤n,m≤100000,
−1000≤数列中元素的值≤1000
输入样例：
5 3
2 1 3 6 4
1 2
1 3
2 4
输出样例：
3
6
10

#include 
using namespace std;
const int N = 100010;

int n, m;
int a[N], s[N];

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);

    for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + a[i]; // 前缀和的初始化

    while (m -- )
    {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n", s[r] - s[l - 1]); // 区间和的计算
    }
    
    return 0;
}

6. 二维前缀和

给定一个矩阵a，通过a的前缀和可得到矩阵a中任意子矩阵的和：

注：该图为矩阵a，且a的下标从1开始存储

二维前缀和模版

S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

模板题 AcWing 796. 子矩阵的和
输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数 n，m，q。
接下来 n 行，每行包含 m 个整数，表示整数矩阵。
接下来 q 行，每行包含四个整数 x1,y1,x2,y2，表示一组询问。
输出格式
共 q 行，每行输出一个询问的结果。
数据范围
1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000
输入样例：
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
输出样例：
17
27
21

#include 
using namespace std;

const int N = 1010;
int a[N][N], s[N][N];

int main() {
    int n, m, q;
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i <= n; i++) 
        for (int j = 1; j <= m; j++) 
            scanf("%d", &a[i][j]);
    for (int i = 1; i <= n; i++) 
        for (int j = 1; j <= m; j++)
            s[i][j] = s[i - 1][j] + s[i][j - 1] + a[i][j] - s[i - 1][j - 1];//得到前缀和
    while (q--) {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        printf ("%d\n", s[x2][y2] - s[x1 -1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
    }
    return 0;
}

7. 一维差分

给定一个数组a，要求对数组a的[l, r]区间上的每一个元素a[i]都加上c:
思路：通过构造一个数组b，使得数组a中的元素是b中元素的前缀和，即a[i] = b[1] + b[2] + ... + b[i]，也称b是a的差分，可通过对b中元素进行操作，将数组a的[l, r]区间上的每一个元素a[i]都加上c。

注：数组的下标从1开始，对数组b初始化时，可将数组a和数组b都视为空数组，并依次将数值a[i]插入a数组的第i个位置，即模版题中的insert(i, i, a[i]。

一维差分模版

给区间[l, r]中的每个数加上c：B[l] += c, B[r + 1] -= c

模板题 AcWing 797. 差分
输入一个长度为 n 的整数序列。
接下来输入 m 个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r] 之间的每个数加上 c。
请你输出进行完所有操作后的序列。
输入格式
第一行包含两个整数 n 和 m。
第二行包含 n 个整数，表示整数序列。
接下来 m 行，每行包含三个整数 l，r，c，表示一个操作。
输出格式
共一行，包含 n 个整数，表示最终序列。
数据范围
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000
输入样例：
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例：
3 4 5 3 4 2

#include 
using namespace std;

const int N = 100010;
int n, m, a[N], b[N];

void insert(int l, int r, int c) {
    b[l] += c;
    b[r + 1] -= c;
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
    //通过依次插入a[i],插入操作可得到b[i]
    for (int i = 1; i <= n; i++) insert(i, i, a[i]);
    
    while (m--) {
        int l, r, c;
        scanf("%d%d%d", &l, &r, &c);
        insert(l, r, c);
    }
    for (int i = 1; i <= n; i++) b[i] += b[i - 1]; //用b[i]来表示原b数组的前i项和
    for (int i = 1; i <= n; i++) printf("%d ", b[i]);
    return 0;
}

8. 二维差分

给定一个矩阵a，要求对矩阵a的某个子矩阵中的每一个元素a[i][j]都加上c:
思路：通过构造一个矩阵b，使得矩阵a中的元素a[i][j]是b中元素的前缀和，即a[i][j] = b[1][1] + b[1][2] + ... + b[i][j - 1] + b[i][j]，也称b是a的二维差分，可通过对b中元素进行操作，将矩阵a的某个子矩阵中的每一个元素a[i][j]都加上c。

注：矩阵的下标从1开始，对矩阵b初始化时，可将矩阵a和矩阵b都视为空矩阵，并依次将数值a[i][j]插入a矩阵的第i行第j列的小矩阵中，即模版题中的insert(i, j, i, j, a[i][j])。

二维差分模版

给矩阵a以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c
思想：通过构造一个矩阵b，使得矩阵a中的元素a[i][j]是矩阵b中元素的前缀和，可通过对b中元素进行操作，将矩阵a的某个子矩阵中的每一个元素a[i][j]都加上c。

b[x1][y1] += c, b[x2 + 1][y1] -= c, b[x1][y2 + 1] -= c, b[x2 + 1][y2 + 1] += c;
然后对矩阵b求前缀和得到矩阵a。

模板题 AcWing 798. 差分矩阵
输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数 x1,y1,x2,y2,c，其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上 c。
请你将进行完所有操作后的矩阵输出。
输入格式
第一行包含整数 n,m,q。
接下来 n 行，每行包含 m 个整数，表示整数矩阵。
接下来 q 行，每行包含 5 个整数 x1,y1,x2,y2,c，表示一个操作。
输出格式
共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。
数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000
输入样例：
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例：
2 3 4 1
4 3 4 1
2 2 2 2

#include 
using namespace std;

const int N = 1010;
int n, m, q, a[N][N], b[N][N], s[N][N];

void insert(int x1, int y1, int x2, int y2, int c) {
    b[x1][y1] += c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main() {
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            scanf("%d", &a[i][j]);
    //矩阵的下标从1开始，对矩阵b初始化时，可将矩阵a和矩阵b都视为空矩阵，
    //并依次将数值a[i][j]插入a矩阵的第i行第j列的小矩阵中
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            insert(i, j, i, j, a[i][j]);
    while (q--) {
        int x1, y1, x2, y2, c;
        scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
        insert(x1, y1, x2, y2, c);
    }
    //通过对矩阵b求前缀和，得到矩阵a
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) 
            s[i][j] = s[i - 1][j] + s[i][j - 1] + b[i][j] - s[i - 1][j - 1];
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) 
            printf ("%d ", s[i][j]);
        puts("");
    }
    return 0;
}

以上模版和笔记均来源：AcWing的算法基础课
链接：https://www.acwing.com/blog/content/277/