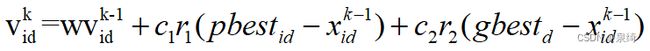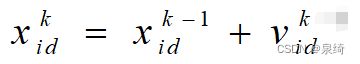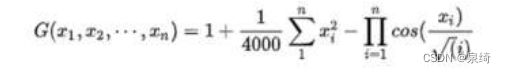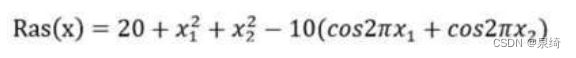实验课一 -- 粒子群算法PSO
文章目录
- 算法说明:
- 算法流程:
- 代码实现:
- 结果展示:
- 结束
算法说明:
我看了下别人写的,这个粒子群算法的思想来源与鸟类捕食
我按我的理解解释一下:
很多只鸟在草原找食物,所有鸟刚开始都不知道食物在哪里,但是鸟儿们很聪明,会互相交流,同时食物有气味,鸟儿们可以通过气味判断自己离食物的远近,闻到气味最大的鸟儿会大叫告诉其他鸟儿,其他鸟儿也往气味最大的鸟身边飞,在它周围区域寻找。
因此,人们就使用这个模型来解决某些问题。也即是让鸟儿帮我们解决问题了
算法流程:
首先,我们要明白算法里面有什么元素:
1,群体规模N,鸟儿的数量
2,维度n,鸟儿所处世界维度,鸟儿是二次元鸟儿的话,那维度就是2
3,惯性权重w,鸟儿是有惯性的,这里表示鸟儿保持速度的能力吧
4,个体学习因子c1,鸟儿的学习能力
5,群体学习因子c2,鸟儿们的学习能力
6,随机数r1,r2,用这两个数保证随机性
7,鸟儿位置X,这个X可以用一个二维数组表示,记录每只鸟儿的位置
8,鸟儿速度V,这个V可以用一个二维数组表示,记录每只鸟儿的速度
9,个体适应度P,这个P可以用一个一维数组表示,记录每只鸟儿的适应度
10,最佳适应度PD,P中最小的值就是当前最佳适应度,当前最佳和历史最佳对比,谁小谁最佳
11,最佳位置pos_best,最佳适应度所在的位置
12,迭代次数k,我们迭代运算的次数
13,满意值t,这个值表示我们能够接受的最小界限,即当最佳适应度PD低于这个值时,我们也大差不差得到了我们满意的结果
接下来开始:
第一步,初始化
鸟儿们的位置和速度都是随机的,但是位置和速度都是有限制的
我们要随机给每只鸟儿安排位置和速度
第二步,算适应度
算适应度需要相应的公式来算,一般情况下,我们要通过我们要解决的问题来算这个适应度
选择当前最佳适应度,选最小的,并保留这个值相对应的位置,同时比对当前最佳适应度和历史最佳适应度,选最小的最佳
第三步,更新速度与位置
我们要根据公式来更新速度与位置
速度公式:
位置更新公式:
要注意的是,当我们更新速度和位置的时候要注意范围,即不要让它们超出范围,它们超出范围的话,就按边界值算
第四步 判断是否结束
当次数达到了规定迭代次数时可以结束
当最佳适应度值小于最小界限的时候可以结束
如果没有满足以上条件,那就返回第二步重新执行
代码实现:
目前只写了python的,能够展示粒子群的移动:
PSO.py
import math
import sys
from math import cos, sqrt
import numpy as np
from PyQt5 import QtCore
from PyQt5.QtWidgets import *
import random
# 1 初始化粒子群参数
import time
class PSO(QWidget):
up = QtCore.pyqtSignal(int, int, np.ndarray)
def __init__(self):
"""
列表:
X: 记录粒子位置(-400,400)
V: 记录粒子速度(-20,20)
P: 记录响应粒子搜索到的最佳位置
PD: 群体最优位置
单值:
Fp: 个体历史最优位置
Fg: 群体历史最优位置
:return:
"""
super().__init__()
# 初始化位置与速度
def ini(self):
self.N = 1000 # 群规模
self.D = 2 # 群维度
self.K = 1000 # 迭代次数
self.w = 1 # 惯性权重
self.c1 = 2 # 个体学习因子
self.c2 = 2 # 群体学习因子
self.r1 = random.uniform(0, 1) # 随机数1
self.r2 = random.uniform(0, 1) # 随机数2
self.MAX_X = 400 # 位置最大
self.MIN_X = -400 # 位置最小
self.MAX_V = 5 # 速度最大
self.MIN_V = -5 # 速度最小
self.X = np.zeros((self.N, self.D))
self.V = np.zeros((self.N, self.D))
self.XN = np.zeros((self.N, self.D))
self.VN = np.zeros((self.N, self.D))
self.P = []
self.PD = 10086
self.ans = []
# self.choose = 1 # 公式选择
for i in range(self.N):
for j in range(self.D):
a = random.uniform(self.MIN_X, self.MAX_X)
self.X[i][j] = a
b = random.uniform(self.MIN_V, self.MAX_V)
self.V[i][j] = b
def check_x(self, x):
if self.MAX_X <= x:
return self.MAX_X
elif self.MIN_X >= x:
return self.MIN_X
return x
def check_v(self, v):
if self.MAX_V <= v:
return self.MAX_V
elif self.MIN_V >= v:
return self.MIN_V
return v
# 公式计算:
def Cal1(self):
for i in range(self.N):
res1 = 0 # X平方
res2 = 1
for j in range(self.D):
res1 = res1 + self.X[i][j]*self.X[i][j]
res2 = res2 * cos(self.X[i][j] / sqrt(j + 1))
ans = 1+1/4000 * res1 - res2
self.P.append(ans)
# 更新速度与位置
def Cal2(self):
for i in range(self.N):
ans = 20 + self.X[i][0]*self.X[i][0] + \
self.X[i][1]*self.X[i][1] - \
10*(cos(2*math.pi*self.X[i][0])+cos(2*math.pi*self.X[i][1]))
self.P.append(ans)
def Update_X_Y(self):
# print("更新")
# 获取下一步速度
for i in range(self.N):
for j in range(self.D):
self.VN[i][j] = self.w * self.V[i][j] + \
self.c1*self.r1*(self.P[i]-self.X[i][j])+\
self.c2*self.r2*(self.P[i]-self.X[i][j])
self.VN[i][j] = self.check_v(self.VN[i][j])
# 更新位置
self.XN[i][j] = self.X[i][j] + self.VN[i][j]
self.XN[i][j] = self.check_x(self.XN[i][j])
# 下一次迭代了,该换换了
for i in range(self.N):
for j in range(self.D):
self.V[i][j] = self.VN[i][j]
self.X[i][j] = self.XN[i][j]
self.P = []
self.r1 = random.uniform(0, 1) # 随机数1
self.r2 = random.uniform(0, 1) # 随机数2
def go1(self):
self.ini()
print("开始,初始化")
print("群初始位置:")
for i in range(self.N):
print(f'X{i+1}: ', end=' ')
print(self.X[i])
print("群初始速度:")
for i in range(self.N):
print(f'V{i + 1}: ', end=' ')
print(self.V[i])
# 最佳适应度公式选择
def go2(self):
if self.choose == 1:
self.Cal1()
elif self.choose == 2:
self.Cal2()
def start(self):
self.go1()
self.tol = 1e-6
for i in range(self.K):
QApplication.processEvents()
# time.sleep(0.1)
print(f"第{i+1}次迭代", end=" ")
self.up.emit(self.N, self.D, self.X)
QApplication.processEvents()
self.go2()
a = min(self.P)
pos = self.X[self.P.index(a)]
if self.PD > a:
self.PD = a
self.ans = pos
if self.PD < self.tol:
break
# print("取群体历史最优解并更新个体位置")
print(f"目前最佳值: {self.PD}")
self.Update_X_Y()
if self.choose == 1:
print("选择公式1")
elif self.choose == 2:
print("选择公式2")
print(f"最终结果: {self.PD}")
print(f'最佳位置: {self.ans}')
# 只显示结果可运行这个
if __name__ == "__main__":
app = QApplication(sys.argv)
PSO = PSO()
PSO.show()
PSO.hide()
PSO.start()
sys.exit(app.exec_())
窗口展示Window.py
import sys
from PyQt5 import QtCore
from PyQt5.QtWidgets import *
from PyQt5.QtGui import QPainter, QColor
from PyQt5.QtCore import Qt, QPoint
from PSO import PSO
_translate = QtCore.QCoreApplication.translate # 翻译函数
class Window(QMainWindow):
def __init__(self):
super().__init__()
self.setWindowTitle("人工智能")
menubar = self.menuBar()
self.menu = menubar.addMenu('粒子群算法')
self.setGeometry(100, 100, 1000, 1000)
self.points = [] # 存储点的列表
self.central_widget = DrawingWidget()
self.setCentralWidget(self.central_widget)
QApplication.processEvents()
self.actionPSO1 = QAction("公式1", self)
self.actionPSO1.triggered.connect(self.PSO1)
self.actionPSO2 = QAction("公式2", self)
self.actionPSO2.triggered.connect(self.PSO2)
self.menu.addAction(self.actionPSO1)
self.menu.addAction(self.actionPSO2)
QApplication.processEvents()
def PSO1(self):
self.central_widget.PSO.choose = 1
self.central_widget.PSO.start()
def PSO2(self):
self.central_widget.PSO.choose = 2
self.central_widget.PSO.start()
class DrawingWidget(QWidget):
def __init__(self):
super().__init__()
self.setGeometry(0, 0, 1000, 1000)
self.points = [] # 存储点的列表
self.PSO = PSO()
self.PSO.up.connect(self.op)
QApplication.processEvents()
def paintEvent(self, event):
painter = QPainter(self)
painter.setRenderHint(QPainter.Antialiasing)
painter.setPen(QColor(0, 0, 255)) # 设置画笔颜色为蓝色
painter.setBrush(Qt.SolidPattern)
for point in self.points:
painter.drawEllipse(point, 2, 2) # 绘制小圆点
def op(self, n, d, lis):
q = []
for i in range(n):
p = QPoint(int(lis[i, 0]+400), int(lis[i, 1]+400))
q.append(p)
self.points = q
self.update()
if __name__ == '__main__':
app = QApplication(sys.argv)
window = Window()
window.show()
sys.exit(app.exec_())
结果展示:
结束
以上仅代表我个人的见解,或许会出错,请见谅并麻烦指出,谢谢