2022年全国研究生数学建模竞赛华为杯C题汽车制造涂装-总装缓存调序区调度优化问题求解全过程文档及程序

2022年全国研究生数学建模竞赛华为杯

C题 汽车制造涂装-总装缓存调序区调度优化问题

原题再现：

  背景介绍
  汽车制造厂主要由焊装车间、涂装车间、总装车间构成，每个车间有不同的生产偏好，如：焊装车间由于车身夹具的限制偏向最小车型及配置切换生产，涂装车间由于喷漆（固定每5辆车清洗喷头、颜色切换也需清洗喷头）限制偏向颜色以5的倍数切换生产，总装车间由于人员工时（不同车型及配置人员工时不同）及硬件（零部件数量等）等限制偏向按照车型及配置按比例切换生产。
  由于各车间的约束不同导致生产调度无法按照同一序列连续生产，特别是涂装车间与总装车间序列差异较大，这就需要在两个车间之间建立一个具有调序功能的缓存区，即PBS（Painted Body Store，汽车制造涂装-总装缓存调序区），用来将涂装车间的出车序列调整到满足总装车间约束的进车序列。
  目前，一天安排上线生产的车辆数介于200-450之间，对于每天要上线生产的车辆，车型、颜色等属性均有变化，目前车型大类有2种，颜色大约有10种，各个车间的产能不定，主要根据当天生产安排调整，涂装车间及总装车间的工艺流程如下：
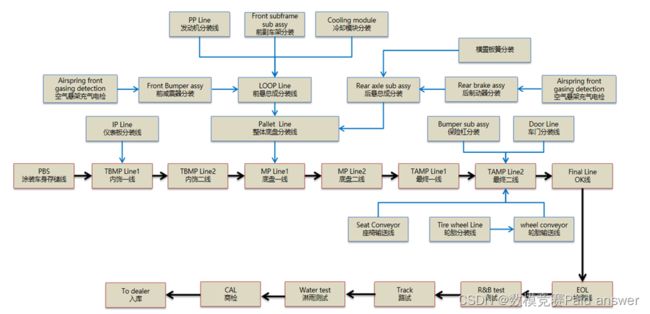
  涂装车间处理喷漆工艺，主要是将涂料涂覆于白车身表面，最终形成涂膜或者漆膜或者涂层。涂装车间的详细流程如图1所示，主要是将白车身经过前处理电泳-中涂-色漆-清漆，最终得到修饰完整的车身。

图1 涂装车间工艺流程图    总装车间处理装配工艺，主要是组装剩余零部件，得到最终成品车辆。总装车间的详细流程如图2所示，主要由内饰线、底盘线、最终线组成，最终经过测试检验后，成品车辆下线入库。

图2 总装车间工艺流程图

  问题描述
  根据涂装车间的出车序列通过PBS调度调整得到总装车间的进车序列。PBS具体信息如图3所示。

图3 涂装-总装缓存调序区（PBS）示意图    PBS由涂装-PBS出车口、接车横移机、进车道6条（每条进车道有10个停车位、FIFO结构）、返回道1条（有10个停车位）、送车横移机及PBS-总装接车口等7个区域组成。各车道距离等分，每车道宽度2米，两相邻车道间间隔1米。横移机运动时的速度保持一致。

  PBS接车横移机：
  1. 将车身从涂装-PBS出车口运送到合适进车道。
  2. 将车身从返回道运送到合适进车道。

  PBS送车横移机：
  1. 将所选择车身从进车道运送到PBS-总装接车口。
  2. 将需调序车身从进车道运送到返回道。

  PBS约束说明：
  1. 送车横移机不能将返回道的车身送入PBS-总装接车口。
  2. 车身在进车道和返回道的移动方向为图中标注方向，不得改变。
  3. 接车横移机和送车横移机上同一时刻分别最多有一个车身。
  4. 接车横移机和送车横移机在完成任意动作后，必须返回中间初始位置，才可以执行下一步动作。
  5. 接车横移机和送车横移机在执行任何动作过程中，均不能被打断。
  6. 当返回道10停车位有车身，同时接车横移机空闲时，优先处理返回道10停车位上的车身。
7. 当若干进车道1停车位有车身等候，同时送车横移机空闲时，优先处理最先到达1停车位的车身。
  8. 如果任意进车道1停车位有车身，那么送车横移机不能设置为空闲状态。
  9. 进车道和返回道每个时刻最多容纳10个车身，每个停车位最多容纳1个车身。
  10. 同一车道内，多个车身在不同停车位上的移动可以不同步进行。
  11. 当某车身所在停车位的下一停车位出现空位时，车身必须立即开始向下一停车位移动。
  12. 车身在进车道和返回道不同停车位之间移动的过程中，不能被调度。

  PBS相关时间数据说明：
  1. 假定车身由横移机卸载到各进车道10停车位或返回道1停车位，以及由各进车道1停车位或返回道10停车位装载到横移机上的时间均可忽略。
  2. 假定车身在涂装-PBS出车口处装载到接车横移机上，以及在4车道出口中间位置处，车身由送车横移机上卸载到PBS-总装接车口，时间均可忽略。
  3. 进车过程：任意车身到达涂装-PBS出车口时，处于最中间位置，正对进车道4，接车横移机把车身从该位置运送至不同进车道10停车位并返回至初始位置，对于1-6进车道，消耗时间分别为[18, 12, 6, 0, 12, 18]秒。
  4. 出车过程：送车横移机从中间初始位置出发，把各进车道1停车位的车身运送至总装-PBS接车口，处于最中间位置，正对进车道4，对于1-6进车道，消耗时间分别为 [18, 12, 6, 0, 12, 18] 秒。
  5. 车进返回道过程：在有需要时，送车横移机从中间初始位置出发，把各进车道1停车位的车身，运送至返回道1停车位，并返回至初始位置，对于1-6进车道，消耗时间分别为 [24, 18, 12, 6, 12, 18]秒。
  6. 车出返回道过程：接车横移机从中间初始位置出发，把返回道10停车位的车身，运送至任意进车道10停车位并返回至初始位置，对于1-6进车道，消耗时间分别为 [24, 18, 12, 6, 12, 18] 秒。
  7. 车移动过程：任意车身在进车道/返回道中，从某一停车位移动至后一停车位，消耗时间为 9秒。

  可选的调度手段：
  1. 接车横移机将当前涂装-PBS出车口队列第一个车身或者返回道10停车位的车身送入任意进车道的10停车位。
  2. 送车横移机将任意进车道1停车位的车送入返回道1停车位或者PBS-总装接车口。
  3. 接车横移机和送车横移机均可以在一段时间内被设置为空闲状态。

  输入输出：
  1. 输入：涂装出车序列清单，可提供多个数据清单。
  2. 输出：每个车身在每一秒所处的区域（涂装-PBS出车口、接车横移机、任意进车道任意停车位、返回道任意停车位、送车横移机、PBS-总装接车口），可构建二维矩阵，里面存储区域代码（如200辆车在第1000秒完成全部调度，则需提交200*1000的矩阵）。矩阵中每一个值为各个区域代码，总的区域代码有74个，区域与代码的对应关系见附件3。车身不在上述74个区域时，对应矩阵值为空白。具体的输出模板文件见附件4（模板文件只是一个示意，示意的场景是50个车身在第100秒完成全部调度，每行代表每个车身各个时间点所处区域，每列代表每个时间点各车身所处区域，其中区域代码没具体填写，具体区域代码见附件3；具体的输出矩阵，需要根据实际数据和算法计算得到，相关数据见附件1-3，附件4只是示意，不代表本题只有50个车身）。由于PBS相关时间说明第1、第2两条假设，会出现同一时刻车身处于若干不同区域的情形，则在输出矩阵该车身该时刻对应格子中填入这些区域中最后一个区域的代码。例如，第0秒，如果涂装-PBS出车口第一个车身（1号车身）被装载到接车横移机上，接着被卸载到4进车道10号车位，则在1号车身第0秒格子中填入4进车道10号车位的区域代码“410”；又例如，第75秒，如果5号车身从送车横移机上被卸载到PBS-总装接车口，则在5号车身第75秒格子中填入PBS-总装接车口区域代码“3”。

  优化目标：
  1. 混动车型间隔2台非混动车型为优，权重系数 0.4。
  2. 四驱车型与两驱车型倾向1:1出车序列，权重系数 0.3。
  3. 返回道使用次数倾向于0，权重系数 0.2。
  4. 倾向总调度时间越短越好，权重系数 0.1。
  注：该权重系数用于多目标得分加权，各权重系数相加等于1。

  优化目标具体量化逻辑：
  设置每个优化目标初始分，根据下述逻辑更新得分后，再乘以相应系数，得到最终加权总分（理论最高分100分）。
  1. 优化目标1（权重系数0.4，初始分100分）：检查出车序列，找到所有混动车身，从出车序列头部按照先后顺序开始算，计算每连续两辆混动车身之间的非混动车身数，不等于2则扣1分。
  2. 优化目标2（权重系数0.3，初始分100分）：对出车序列进行分块，判断每一分快中的四驱车型与两驱车型之比是否满足1:1，若不满足，则扣1分。对出车序列分块的依据是：如果序列以4开头，则根据从2变为4将序列进行分块；如果序列以2开头，则根据从4变为2将序列进行分块。 例如：如果出车序列为 442242444224(4代表四驱车型，2代表两驱车型)，则该序列分块结果为：4422,42,44422，4，最后两个分块44422和4都不满足1:1，扣2分。
  3. 优化目标3（权重系数0.2，初始分100分）：统计返回道使用次数，每使用一次扣1分。
  4. 优化目标4（权重系数0.1，初始分为100分）：假设出车队列长度为C， 第一辆车身进入涂装-PBS出车口时刻记为零，以最后一个车身进入PBS-总装接车口的时刻T为总完成时间，其理论最快完成时间为 9C+72(全部走进车道4，出车序列与入车序列相同)，其时间惩罚值设置为 0.01 × (T – 9C-72)， 最后目标得分为 100 – 时间惩罚值。

  请建模完成以下优化问题：
  问题 1：严格按照PBS约束说明及相关时间数据说明，根据涂装出车序列，考虑PBS区域调度能力及限制，建立PBS优化调度模型，使得总装进车序列尽可能满足总装生产需求。给出将你们的优化调度方案分别应用于附件1和附件2数据的得分结果，并将使用附件1和附件2两套数据的调度输出结果按照附件4格式分别存入result11.xlsx和result12.xlsx。

  问题 2：如果去除PBS约束说明中第6、7两条约束，其余约束不变，根据涂装出车序列，考虑PBS区域调度能力及限制，建立PBS优化调度模型，使得总装进车序列尽可能满足总装生产需求。给出将你们的优化调度方案分别应用于附件1和附件2数据的得分结果，并将使用附件1和附件2两套数据的调度输出结果按照附件4格式分别存入result21.xlsx和result22.xlsx。

  数据说明：本题共有两套数据，附件1数据是生产数据脱敏后的正常数据，附件2数据是为了测试模型和算法的适应性而调整后的数据。

整体求解过程概述(摘要)

  工业领域中，利用缓存区调序是优化工业流程，节省工业成本的重要手段。随着新能源技术的发展，汽车工业在生产中的地位逐渐提高，而汽车制造涂装-总装缓存调序作为汽车制造流程中极为重要的一部分，其调序区调度优化问题有着重要的研究意义，本文通过分析车辆调度工作流程建立了基于动态规划的多目标优化调度模型。
  针对问题一，通过分析车辆的调度流程以及相关约束条件，以每辆车被接车横移机将要运往的目标车道以及该车是否要通过返回道作为决策变量，建立每一时刻进车道与返回道上车位车辆的时间状态矩阵，以第一辆车被接车横移机处理为初始时刻，利用接车横移机和送车横移机工作时间矩阵，模拟出每一辆车在随时间变化的位置以及状态。由于接车横移机优先处理返回道 10 号位上的车辆，送车横移机优先处理先到 1 号位的车辆，则可通过返回道使用次数对车辆的序列进行迭代改变。对优化目标一（），利用卷积的思想处理，即设置一个卷积核，将其公式化；对优化目标二（），建立2 = ()，其主要通过既定的算法计算得分；对优化目标三（），将每辆车是否使用返回道统计即可得到；对优化目标四（），通过进车道与返车道上每个车位的时间矩阵，利用时间变量，对整个车道调度过程进行递推模拟，将车辆的输出序列进行迭代，最终求得整个调度流程所消耗的时间，以此建立基于动态规划的多目标优化调度模型。
  考虑到接车横移机与送车横移机工作时选择不同车道所消耗的时间差，利用灰狼算法设置迭代次数对模型进行求解，得到附件 1 最高得分为 18.916 分，其调度流程总用时3056 秒，返回道总共使用 6 次，附件 2 最高得分为 44.469 分，其调度流程总用时 2996s，返回道总共使用 6 次。
  针对问题二，取消约束 6 后，接车横移机不再优先处理返车道 10 号位上的车，引入新的决策变量，即返回道上每辆车到达 10 号位后的等待时间，接车横移机每次工作时，首先判断返回道 10 号位上有无车辆，当返回道上 10 号位有车时，接车横移机到达返回道上的时刻需大于返回道上 10 号位上车的等待时间，才会处理返回道上的车，否则处理涂装-PBS 出车口处的车辆。取消约束 7 后，送车横移机将不再优先处理先到达 1 号位的车辆，即在处理完上一辆车后需对当前时刻所有车道 1 号位进行判断，如果 1 号位上的车辆大于 1，则需进行选择，此时将位于 1 号位的每一辆汽车分别模拟当其送出或送往返回道以后输出序列，然后求得当前情况每一辆车的得分，对得分进行排序，重新规定他们的输出顺序。以问题一所建立的模型为基础，添加上述新的决策变量和约束条件建立基于动态规划的多目标优化调度模型。
  利用灰狼算法设置迭代次数对模型进行求解，得到附件 1 最高得分为 19.459 分，其调度流程总用时 3056 秒，返回道总共使用 8 次；附件 2 最高得分为 45.78 分，其调度流程总用时 3014 秒，返回道总共使用 4 次。与模型一求解结果进行比较，其收敛度更快，结果更好。
  综上，本文通过分析车道调度流程，利用了较少的决策变量，建立了基于动态规划的多目标优化调度模型，较好的拟合了车道调度流程，利用所给数据计算出最后得分，并通过与理论最优解进行比较，对模型进行了评价。

模型假设：

  假设 1：假设汽车车型对总装车间的进车序列没有影响；
  假设 2：假设接车、送车横移机在装载车身到进车道 10 停车位或返回道 1 停车位的时间忽略不计；
  假设 3：假设车身从涂装-PBS 出车口处装载到接车横移机上，以及在 4 车道出口中间位置处，车身由送车横移机上卸载到 PBS-总装接车口，时间均忽略不计；
  假设 4：横移机运动时的速度保持一致；
  假设 5：假设在整个 PBS 过程中，接车、送车横移机等装置不会出现故障；
  假设 6：车辆在车道上从前一车位移动到后一车位的 9s 内始终处于前一车位，到第 9s 时处于后一车位；

问题分析：

  问题一分析:
  首先，对车辆在 PBS 流程中的运动轨迹进行分析，车辆运作流程如图所示。

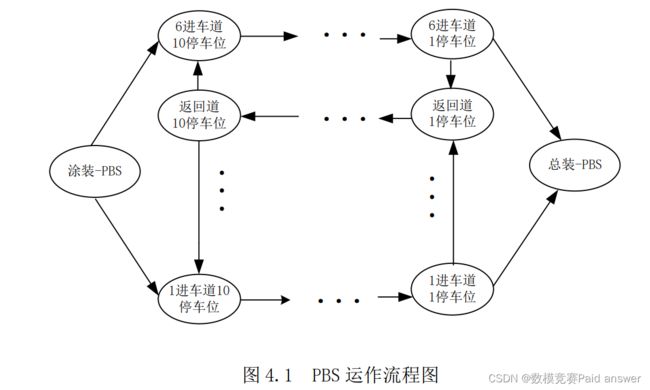
  其次，根据 PBS 相关时间数据分析，可得接车横移机从涂装-PBS 口出发，将车运送到不同进车道上消耗的时间差最大为 9s。所以，只要当车辆被运送到任意进车道后，在不使用返回道的情况下，其送车顺序将与接车顺序一致，而每使用返回道一次，就会改变一次出车顺序，即当某一辆车被送车横移机决定送到返回道上时，整个车辆的出车顺序将会被改变，接车横移机从返回道中取车总共取了 v 次，则整个出车顺序() ={1,2,3, … (), … , }就改变了 v 次，而这种改变并非瞬间改变，而是当汽车决定被送车横移机移动到返回道上开始改变，汽车移动到返回道上的 10 号位后，被接车横移机插入队列完成改变。
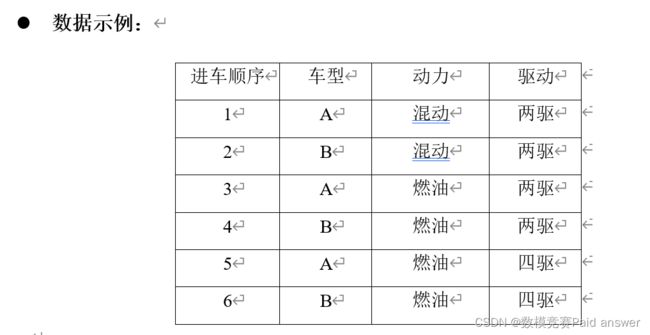
  最后，从优化目标出发，对附件中的生产数据进行分析，考虑满足单目标条件下的扣分情况，以此得到一个参考得分。以附件 1 为例，混动车身与燃油车身的数量之比为2:1，四驱与两驱车型的数量之比近似 10:1。从第一个目标出发，即 n 个混动车身需要(n-1)*2 个燃油车身，则有 54 个混动车身可以满足要求，剩余 158 个不满足要求，依据量化逻辑进行扣分，需要扣158 × 1 × 0.4 = 63.2分，在完全满足其他目标时，可得 36.8分。从第二个目标出发，即四驱与两驱车型的出车序列为 1:1，则有 29 个两驱车型满足要求，剩余 260 个不满足要求，依据量化逻辑进行扣分，需要扣260 × 1 × 0.3 = 78分，在完全满足其他目标时，可得 22 分。

  问题二分析
  在问题一的基础上，减少两条约束，即返回道 10 停车位和进车道 1 停车位上的车辆不需要立刻处理。针对约束条件 6，取消该约束时，将会出现在接车横移机空闲时，返回道 10 停车位和涂装-PBS 出车口都有车等待处理。针对约束条件 7，取消该约束时，汽车被送车横移机处理的控制流程就会发生改变，即不止一个车道的 1 停车位上有待处理的车，则送车横移机需要判断优先处理顺序。

模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：

部分Python程序如下:

import numpy as np
import pandas as pd
import time
import matplotlib.pyplot as plt
data_1 = pd.read_excel('附件 1.xlsx')
data_2 = pd.read_excel('附件 2.xlsx')
data_1 = np.array(data_1)
data_2 = np.array(data_2)
data_1[:,2] = np.where(data_1[:,2]=='燃油',0,1)
data_1[:,3] = np.where(data_1[:,3]=='两驱',0,1)
data_2[:,2] = np.where(data_2[:,2]=='燃油',0,1)
data_2[:,3] = np.where(data_2[:,3]=='两驱',0,1)
class GWO():
 def __init__(self,dim=6000,maxiter=200,size=40,lb=0,ub=0.999999999):
 self.dim = dim
 self.X = np.random.uniform(low=lb,high=ub,size=(size,dim))
 self.alpha_wolf_pos = None
 self.beta_wolf_1_pos = None
 self.beta_wolf_2_pos = None
 self.maxiter = maxiter
 self.size = size
 self.lb = lb
 self.ub = ub
 self.gen_best_y = np.zeros(shape=(self.maxiter+1,))
 self.gen_best_X = np.zeros(shape=(self.maxiter+1,dim))
 self.gen_min_y = None
 self.gen_min_x = None
 self.time_in_out = np.array([18, 12, 6, 0, 12, 18]) / 3
 self.time_fan = np.array([24, 18, 12, 6, 12, 18]) / 3
 self.timeChedaoToHyj = self.time_in_out / 2
 self.time_fanToChedao = np.array([4, 3, 2, 1, 1, 2])
 self.time_0 = 3
 self.gold1 = None
 self.gold2 = None
 self.gold3 = None
 self.gold4 = None

def fitness(self,data):
 self.curY = np.zeros(shape=(self.size,))
 for i in range(self.size):
 ans, outLine, needNunberFan,costtime = self.genX(maxiter=self.dim/2, data=data,renwu=self.X[i],cur=i)
 curGold,self.gold1,self.gold2,self.gold3,self.gold4 = self.getGold(outLine, needNunberFan, data, costtime)
 self.curY[i] = -1*curGold
 def getCurWolf(self,t):
 index = self.curY.argsort()
 self.alpha_wolf_pos = self.X[index[0]]
 self.beta_wolf_1_pos = self.X[index[1]]
 self.beta_wolf_2_pos = self.X[index[2]]
 def getNewX(self,t):
 r_1_a = np.random.uniform(low=0,high=1,size=(self.size,self.dim))
 r_1_b_1 = np.random.uniform(low=0,high=1,size=(self.size,self.dim))
 r_1_b_2 = np.random.uniform(low=0,high=1,size=(self.size,self.dim))
 r_2_a = np.random.uniform(low=0,high=1,size=(self.size,self.dim))
 r_2_b_1 = np.random.uniform(low=0,high=1,size=(self.size,self.dim))
 r_2_b_2 = np.random.uniform(low=0,high=1,size=(self.size,self.dim))
 a = 2*(1-t/self.maxiter)
 A_a = 2*a*r_1_a-a
 A_b_1 = 2*a*r_1_b_1-a
 A_b_2 = 2 * a * r_1_b_2 - a
 C_a = 2*r_2_a
 C_b_1 = 2*r_2_b_1
 C_b_2 = 2*r_2_b_2
 distance_a = np.abs(C_a * self.alpha_wolf_pos - self.X)
 distance_b_1 = np.abs(C_b_1 * self.beta_wolf_1_pos - self.X)
 distance_b_2 = np.abs(C_b_2 * self.beta_wolf_2_pos - self.X)
 X_a = self.alpha_wolf_pos - A_a * distance_a
 X_b_1 = self.beta_wolf_1_pos - A_b_1 * distance_b_1
 X_b_2 = self.beta_wolf_2_pos - A_b_2 * distance_b_2
 new_X = (X_a+X_b_1+X_b_2)/3
 new_X = np.where(new_X<self.lb,self.lb,new_X)
 new_X = np.where(new_X>self.ub,self.ub,new_X)
 return new_X
 def chedaoOneToOne(self,x, result, time_i):
 xAfter0 = x[:, 3:-1]
 xIndex = np.where(xAfter0 != -1)
 curVar = (xIndex[0].reshape(-1, 1) + 1) * 10 + 10 - (xIndex[1].reshape(-1, 1) + 3) // 3
 curVar = curVar.reshape(-1, 1)
result[xAfter0[xIndex[0], xIndex[1]].astype(int), time_i * 3:time_i * 3 + 3] = curVar
 xIndex = np.where(x[:, :3] != -1)
 result[x[xIndex[0], xIndex[1]].astype(int), time_i * 3:time_i * 3 + 3] = (xIndex[0].reshape(-1,
 1) + 1) * 100 + 10
 xIndex = np.where(x[:, -1] != -1)
 result[x[xIndex[0], -1].astype(int), time_i * 3:time_i * 3 + 3] = (xIndex[0].reshape(-1, 1) + 1) * 10 + 1
 return result
 def fanOneToOne(self,x, result, time_i): ###x 表示每个车道车位上对应的车的编号，-1 为没车
 curVar = x[0]
 if curVar != -1:
 result[int(curVar), time_i * 3:time_i * 3 + 3] = 710 ###更新反车道 10 车位
 curVar = x[1:]
 curVarIndex = np.where(curVar != -1)[0] ###找到有车的车位
 result[curVar[curVarIndex].astype(int), time_i * 3:time_i * 3 + 3] = 70 + 9 - curVarIndex.reshape(-1,
 1) // 3 ###更新反车道 1-9 车位
 return result
 def Outputresult(self,x):
 x_Index = np.where(x != 3)[1].max()
 return x[:, :x_Index + 3]
 def getGold(self,x, number, data, costTime):
 l = len(x)
 data = data[:, 2:]
 x_list = []
 for i in range(l):
 x_list.append(data[x[i], 1])
 item2 = self.z2(x_list)
 x_list = []
 for i in range(l):
 x_list.append(data[x[i],0])
 item1 = self.z1(x_list)
 result = (100-item1)*0.4+(100-item2)*0.3+(100-number)*0.2+0.1*(100-(costTime-2934)*0.01)
 return result,(100-item1)*0.4,(100-item2)*0.3,(100-number)*0.2,0.1*(100-(costTime-2934)*0.01)
 def z1(self,data):
 result = 0
 cc = 0
 data = np.array(data)
 a = np.where((data == 1))
 for i in range(1, len(a[0])):
 if a[0][i] - a[0][i - 1] == 3；
 result = result + 1
 else:
 cc = cc + 1
 rrr = cc
 return rrr
 def z2(self,list1):
 result = [0]
 rr = []
 flag = 0
 j = 1
 rrr = 0
 R = 0
 for i in range(1, len(list1)):
 if list1[i] == list1[i - 1]:
 flag += 1
 else:
 flag = 0
 result.append(flag)
 result.append(0)
 for i in range(1, len(result)):
 if result[i] <= result[i - 1]:
 rr.append(result[i - 1] + 1)
 while j < len(rr):
 if rr[j] == rr[j - 1]:
 rrr = rrr + 1
 else:
 R = R + 1
 j = j + 2
 if len(rr) % 2:
 R = R + 1
 return R
 def genX(self,renwu,maxiter, data,cur):
 renwu = renwu.reshape(-1,2)
 m, n = data.shape ###数据长度
 outputLine = [] ###输出队列
 inputHyjToChedaoGang = [] ###刚刚从输入横移机放入车道
 outputHyjTofanGang = [] ###刚刚从输出横移机放入反车道
 result = np.zeros(shape=(m, int(maxiter * 3)))
 chedaoIndex = np.zeros(shape=(6, 28)) - 1 ###车道上车的编号，没车就是-1
 fanIndex = np.zeros(28) - 1 ###返回道上车位的编号，没车为-1
chedaoState = np.zeros(shape=(6, 28)) ###车道上有无车，有车 1，没车 0
 fanState = np.zeros(28) ###反车道上的状态，有车 1，没车 0
 fanNunber = 0 ###使用返回道次数
 resultHyjStarEnd = np.zeros(shape=(m, 5)) ###0 还没出，1 在横移机上，2 在车道上，3 在输出横移机，4 在终
点
 resultHyjStarEnd[:, 0] = 1
 ifStar = np.zeros(m)
 ifStar[0] = 1 ###
 if_fanStar = 0 ###返回车道的第 10 车位状态，0 为空，1 为满
 ifInputHyj = 0 ###入口横移机是否在工作，0 为空，1 为满
 ifOutputHyj = 0 ###出口横移机是否在工作，0 为空，1 为满
 timeFanArrive = 0 ###返回道到达时间
 fromWhere = 0 ###输入横移机上的车的来源，0 表示 PBS，1 表示返回道
 arriveIndex = [] ###到达最后一个车位的车道顺序
 outOrInput = 0 ###横移机准备把车送出去还是送回返回道，0 表示去返回道，1 表示送出去
 inputHyjCar = -1 ###初始化输入横移机上的车的编号，-1 表示没有车
 OutHyjCar = -1 ###初始化输出横移机上的车编号，没车表示-1
 PbsCarCur = 0 ###初始化 PBS->输入横移机上的编号，第一辆为 0
 arrive10Chewei = np.zeros(m)
 i = 0
 while i < maxiter:
 ifRunChedao = np.zeros(shape=(6, 27)) ###可移动的车道,1 表示可移动，0 表示不可移动,这得对约束的理解
进行修改
 ifRunFan = np.zeros(27) ###返回道是否可移动,1 表示可移动，0 表示不可移动
 if ifInputHyj == 0: ###如果输入横移机空闲
 ifRunChedao_0 = chedaoState[:, :3] ###10 车位上的车道状态
 ifRunChedao_0 = np.where(ifRunChedao_0 == 1) ###10 车位上有车的索引
 needQueren = []
 canRunChedao = [3,2,4,1,5,0] ###可选择车道
 for j in range(6):
 if j in ifRunChedao_0[0]:
 canRunChedao.remove(j) ###剩下一定能走的车道
 needQueren.append(j) ###需要计算时间确认的车道
 ###这里根据来源不同进行不同的计算可选择车道
 ###计算可选择车道这里有问题
 # if if_fanStar == 1: ###10 号车位返回道有车
 # if needQueren:
 # for j in range(len(needQueren)):
 # if time_fanToChedao[needQueren[j]] > 3 - ifRunChedao_0[needQueren[j], 1]:
 # canRunChedao.append(needQueren[j])
 if PbsCarCur < m:
 if if_fanStar == 0: ###当返回道的 10 车位为空时，
 #canRunChedao = [3,2,4,1,5,0] ###输入横移机可选择的部分
 canRunChedao.append('等待')
chooseChedao = renwu[i,0] * len(canRunChedao) ###根据既定任务选择车道
 chooseChedao = canRunChedao[int(chooseChedao)] ###选择进哪个车道
 if if_fanStar == 1:###返回车道不为空
 chooseChedao = renwu[i,0] * len(canRunChedao) ###根据既定任务选择车道
 chooseChedao = canRunChedao[int(chooseChedao)] ###选择进哪个车道
 if chooseChedao != '等待': ###如果不选择等待
 timeInputHyjNeed = self.time_in_out[chooseChedao] ###所选择的车道需要花的时间
 timeInputHyjWorkCur = i ###输入横移机开始工作的时间
 if PbsCarCur < m: ###仓库内还有车
 if if_fanStar == 0: ###如果返回道 10 车位没车
 ifInputHyj = 1 ###立刻可以拿车，将横移机置为工作状态
 fromWhere = 0 ###记录数据来源，从仓库来的数据
 result[PbsCarCur, i * 3:(i + 1) * 3] = 1 ###记录数据
 inputHyjCar = PbsCarCur ###输入横移机从仓库拿车，更新输入横移机上车的序号
 PbsCarCur += 1 ###下一辆仓库的出车序号
 if if_fanStar == 1:
 fromWhere = 1 ######记录数据来源，从反车道来的数据
 ifInputHyj = 0 ###此时还没装车，为了方便处理所以将输入横移机的工作状态置为 0，实际此时为 1
 if i >= timeFanArrive + 1: ###输入横移机到达反车道 10 车位
 inputHyjCar = fanIndex[0] ###输入横移机此时携带的车的序号
 result[int(inputHyjCar), i * 3:(i + 1) * 3] = 1 ###记录结果
 fanIndex[0] = -1 ###车被搬走，所以返回道 10 车位没有车，用-1 表示
 fanState[0] = 0 ###车被搬走，返回道 10 车位没车，0 表示没车
 if_fanStar = 0 ###车被搬走，返回道 10 车位没车，0 表示没车
 timeInputHyjWorkCur = i ###输入横移机从返回道接受车的时间点
 ifInputHyj = 1 ###输入横移机在工作
 if ifInputHyj == 1: ###如果输入横移机在工作
 if fromWhere == 0: ###如果从仓库来的
 if inputHyjCar != -1:
 result[int(inputHyjCar), i * 3:(i + 1) * 3] = 1 ###记录结果
 if i == (timeInputHyjWorkCur + timeInputHyjNeed / 2): ###如果输入横移机送到目标车道
 inputHyjToChedaoGang.append(chooseChedao) ###输入横移机刚刚把车放在指定车道
 chedaoState[chooseChedao, 0] = 1 ###将所选择车道的 10 车位置为 1
 chedaoIndex[chooseChedao, 0] = inputHyjCar ###更新车道上的车的序号
 result[inputHyjCar, i * 3:(i + 1) * 3] = (1 + chooseChedao) * 100 + 10 ###记录结果
 inputHyjCar = -1 ###输入横移机此时不再有车
if i >= timeInputHyjNeed + timeInputHyjWorkCur: ###输入横移机回到原来位置时
 ifInputHyj = 0 ###输入横移机工作转态置为 0
 timeFanArrive = i ###修改的地方#####################
 if fromWhere == 1:
 if i == timeInputHyjWorkCur + self.time_fanToChedao[int(chooseChedao)]:
 chedaoState[chooseChedao, 0] = 1 ###从返回道的 10 车位来的车，由输入横移机放到选择的车道中
 chedaoIndex[chooseChedao, 0] = inputHyjCar ###更新被选择的车道上车的编号
 inputHyjToChedaoGang.append(chooseChedao) ###输入横移机刚刚把车放在指定车道
 result[int(inputHyjCar), i * 3:i * 3 + 3] = chooseChedao * 100 + 10 ###更新结果
 inputHyjCar = -1 ###输入横移机上没有车
 if i >= self.time_fan[chooseChedao] - 1 + timeInputHyjWorkCur: ###输入横移车回到开始的位置时
 ifInputHyj = 0
 timeFanArrive = i ###修改的地方######################
 if ifOutputHyj == 0 and len(arriveIndex) != 0: ###如果输出横移机空闲，且 1 车位内有车
 timeOutputHyjWorkCur = i ###输出横移机开始工作的时间
 timeOutputHyjNeed = self.time_in_out[arriveIndex[0]] / 2 ###输出横移机需要到达指定车道所花的时间
 timeOutputHyjChedaoToFan = self.time_fanToChedao[arriveIndex[0]] ###输出横移机从指定车道送到返回
道的时间
 ifOutputHyj = 1 ###输出横移机工作状态置为 1
 if ifOutputHyj == 1:
 if i == timeOutputHyjWorkCur + timeOutputHyjNeed: ###输出横移机到达 1 车位
 ###到达 1 车位后对输出还是回返回道进行判断
 if fanState[25:].any() == 1:
 outOrInput = 1
 if fanState[25:].any() != 1:
 if renwu[i,1] <=0.5:
 outOrInput =1
 if renwu[i,1] >0.5:
 outOrInput = 0 ###0 表示去返回道，1 表示直接出去
 result[int(chedaoIndex[int(arriveIndex[0]), -1]), i * 3:i * 3 + 3] = 2 ###车到了输出横移机身上，记录结果
 OutHyjCar = chedaoIndex[int(arriveIndex[0]), -1] ###输出横移机上面车的序号
 chedaoState[int(arriveIndex[0]), -1] = 0 ###车道状态改变
 chedaoIndex[int(arriveIndex[0]), -1] = -1 ###车道上对应车位的车的序号置为-1（-1 表示没有车）
 arriveIndex.pop(0) ###到达最后一个车位的车道顺序里去除被接走的车
if i >= timeOutputHyjWorkCur + timeOutputHyjNeed:
 ###outOrInput 这个规则及约束还没写
 if outOrInput == 0: ###把车送到返回道
 if i < timeOutputHyjWorkCur + timeOutputHyjNeed + timeOutputHyjChedaoToFan: ###车在输出横移
机上
 result[int(OutHyjCar), i * 3:i * 3 + 3] = 2
 if i == timeOutputHyjWorkCur + timeOutputHyjNeed + timeOutputHyjChedaoToFan: ###把车从输出横
移机放到返回道
 arrive10Chewei[int(OutHyjCar)] += 1 ###车到达返回道，这表明车已用掉一次返回的机会
 result[int(OutHyjCar), i * 3:i * 3 + 3] = 71
 outputHyjTofanGang.append(27) ###刚刚把车从输出横移机放到反车道
 fanState[-1] = 1 ###返回车道的 1 车位放车
 fanIndex[-1] = OutHyjCar ###返回车道上的 1 车位上车的序号
 OutHyjCar = -1 ###输出横移机不再有车
 fanNunber += 1
 if i == timeOutputHyjWorkCur + timeOutputHyjNeed + timeOutputHyjChedaoToFan + 1: ###输出横移
机结束工作
 ifOutputHyj = 0
 ###输出横移机送出去
 if outOrInput == 1:
 if i < timeOutputHyjWorkCur + 2 * timeOutputHyjNeed: ###输出横移机还未到达指定车道，车还在横
移机上
 result[int(OutHyjCar), i * 3:i * 3 + 3] = 2
 if i == timeOutputHyjWorkCur + 2 * timeOutputHyjNeed: ###输出横移机成功把车送出去
 result[int(OutHyjCar), i * 3:i * 3 + 3] = 3 ###更新记录
 outputLine.append(int(OutHyjCar)) ###输出队列添加上刚刚送出去的车
 ifOutputHyj = 0 ###输出横移机结束工作
 OutHyjCar = -1 ###输出横移机上没有车，置为-1
 ###车道能否移动判断矩阵
 for j in range(6):
 for j_index in range(9):
 if j_index == 0:
 if chedaoState[j, -1] == 0: ###1 车位没车的话，这条道一定可以走
 ifRunChedao[j] = 1
 break
 if j_index > 0:
 if chedaoState[j, 27 - j_index * 3:30 - j_index * 3].any() == 0: ###当前车位没车的话，后面的车一定可
以往前走
ifRunChedao[j, :27 - j_index * 3] = 1
 break
 ifRunChedao = np.append(ifRunChedao, np.zeros(shape=(6, 1)), axis=1) ###1 车位不能通过车道往前走
 ###返回道可否移动的判断矩阵
 for j in range(9):
 if j == 0:
 if fanState[0] == 0: ###返回道 10 车位没车时，返回道都可移动
 ifRunFan[:] = 1
 break
 if j > 0:
 if fanState[j * 3 - 2: j * 3 + 1].any() == 0: ###返回道当前车位没车时，小于该车位的车位可移动
 ifRunFan[j * 3:] = 1
 break
 ifRunFan = np.append(np.zeros(1), ifRunFan) ###返回道 10 车位的车不可通过返回道移动
 ###车道状态改变
 haveCarCanGo = ifRunChedao * chedaoState ###有车且能走的车
 if inputHyjToChedaoGang:
 haveCarCanGo[int(chooseChedao), 0] = 0 ###刚刚到车道的车不能走
 inputHyjToChedaoGang.pop() ###取消刚刚到车道这个‘刚刚’的状态
 haveCarCanGoIndexOldChedao = np.where(haveCarCanGo == 1)[0]
 haveCarCanGoIndexOldChewei = np.where(haveCarCanGo == 1)[1]
 haveCarCanGoIndexNewChewei = haveCarCanGoIndexOldChewei + 1
 chedaoState[haveCarCanGoIndexOldChedao, haveCarCanGoIndexNewChewei] = 1
 chedaoState[haveCarCanGoIndexOldChedao, haveCarCanGoIndexOldChewei] = 0
 ###调整车道上车的序号
 chedaoIndex[haveCarCanGoIndexOldChedao, haveCarCanGoIndexNewChewei], chedaoIndex[
 haveCarCanGoIndexOldChedao, haveCarCanGoIndexOldChewei] = \
 chedaoIndex[haveCarCanGoIndexOldChedao, haveCarCanGoIndexOldChewei], chedaoIndex[
 haveCarCanGoIndexOldChedao, haveCarCanGoIndexNewChewei]
 result = self.chedaoOneToOne(chedaoIndex, result, i) ###记录车道上车的位置
 chedaoLastChewei = chedaoState[:, -1] ###1 车位上的状态
 chedaoLastChewei = np.where(chedaoLastChewei == 1)[0] ###1 车位上有车的车道
 for j in chedaoLastChewei:
 if j not in arriveIndex: ###已经在到达 1 车位的队列则不再添加
 arriveIndex.append(j) ###到达 1 车位的队列添加新到达的
 ###反车道状态改变
 haveFanCarCanGo = ifRunFan * fanState ###反车道上有车且能走的车
if outputHyjTofanGang:
 haveFanCarCanGo[-1] = 0 ###刚刚到反车道的车不能动
 outputHyjTofanGang.pop() ###取消刚刚到反车道的这个‘刚刚的’状态
 haveCarCanGoIndexOldfan = np.where(haveFanCarCanGo == 1)[0] ###反车道上有车的车位
 haveCarCanGoIndexNewfan = haveCarCanGoIndexOldfan - 1 ###反车道上的车移动后的车位
 fanState[haveCarCanGoIndexOldfan] = 0
 fanState[haveCarCanGoIndexNewfan] = 1
 if fanState[0] == 1: ###返回道 10 车位有车时
 if_fanStar = 1 ###返回道 10 车位修改为有车
 fanIndex[haveCarCanGoIndexOldfan], fanIndex[haveCarCanGoIndexNewfan] = \
 fanIndex[haveCarCanGoIndexNewfan], fanIndex[haveCarCanGoIndexOldfan] ###调整反车道上车的序号
 if fanState[0] == 1:
 if_fanStar = 1
 if fanState[0] == 0:
 if_fanStar = 0
 if inputHyjCar != -1:
 result[int(inputHyjCar), i * 3:i * 3 + 3] = 1
 if OutHyjCar != -1:
 result[int(OutHyjCar), i * 3:i * 3 + 3] = 2
 result = self.fanOneToOne(fanIndex, result, i) ###记录返回道上车的位置
 result[outputLine, i * 3:i * 3 + 3] = 3 ###记录车出去后，车所在的位置
 if i >750:
 if len(np.where(result[:, i * 3] != 3)[0]) == 0:
 result = result[:, :(i + 1) * 3]
 break
 if i == maxiter-2:
 #print(0)
 #print(i)
 self.X[cur]= np.random.uniform(low=self.lb,high=self.ub,size=(self.dim,))
 renwu = self.X[cur]
 renwu = renwu.reshape(-1,2)
 i = 0
 outputLine = [] ###输出队列
 inputHyjToChedaoGang = [] ###刚刚从输入横移机放入车道
 outputHyjTofanGang = [] ###刚刚从输出横移机放入反车道
 result = np.zeros(shape=(m, int(maxiter * 3)))
 chedaoIndex = np.zeros(shape=(6, 28)) - 1 ###车道上车的编号，没车就是-1
fanIndex = np.zeros(28) - 1 ###返回道上车位的编号，没车为-1
 chedaoState = np.zeros(shape=(6, 28)) ###车道上有无车，有车 1，没车 0
 fanState = np.zeros(28) ###反车道上的状态，有车 1，没车 0
 fanNunber = 0 ###使用返回道次数
 resultHyjStarEnd = np.zeros(shape=(m, 5)) ###0 还没出，1 在横移机上，2 在车道上，3 在输出横移机，4
在终点
 resultHyjStarEnd[:, 0] = 1
 ifStar = np.zeros(m)
 ifStar[0] = 1 ###
 if_fanStar = 0 ###返回车道的第 10 车位状态，0 为空，1 为满
 ifInputHyj = 0 ###入口横移机是否在工作，0 为空，1 为满
 ifOutputHyj = 0 ###出口横移机是否在工作，0 为空，1 为满
 timeFanArrive = 0 ###返回道到达时间
 fromWhere = 0 ###输入横移机上的车的来源，0 表示 PBS，1 表示返回道
 arriveIndex = [] ###到达最后一个车位的车道顺序
 outOrInput = 0 ###横移机准备把车送出去还是送回返回道，0 表示去返回道，1 表示送出去
 inputHyjCar = -1 ###初始化输入横移机上的车的编号，-1 表示没有车
 OutHyjCar = -1 ###初始化输出横移机上的车编号，没车表示-1
 PbsCarCur = 0 ###初始化 PBS->输入横移机上的编号，第一辆为 0
 arrive10Chewei = np.zeros(m)
 i += 1
 return result, outputLine, fanNunber,result.shape[1]
 def run(self,data):
 t1 = time.time()
 for i in range(self.maxiter):
 self.fitness(data)
 self.gen_best_y[i] = np.min(self.curY)
 self.gen_best_X[i, :] = self.alpha_wolf_pos
 self.getCurWolf(i)
 self.X = self.getNewX(i)
 #if i >10 and self.gen_best_y[i] > self.gen_best_y[i-10]-0.0001:
 #break
 if i %10 ==0:
 print(i)
 t2 = time.time()
 if t2-t1 > 6000:
 break
 self.fitness(data)
 self.gen_best_y[i+1] = np.min(self.curY)
self.gen_best_y = self.gen_best_y[:i+1]
 self.gen_best_X[i+1, :] = self.alpha_wolf_pos
 self.gen_best_X = self.gen_best_X[:i+1,:]
 index = np.argmin(self.curY)
 best_x = self.X[index]
 best_y = self.curY[index]
 gen_min_y_index = self.gen_best_y.argmin()
 self.gen_min_y = self.gen_best_y[gen_min_y_index]
 self.gen_min_x = self.gen_best_X[gen_min_y_index]
 return best_x,best_y
model = GWO(maxiter=400)
best_x,best_y = model.run(data_1)
plt.plot(model.gen_best_y)
plt.show()
result, outputLine, fanNunber,costTime=model.genX(maxiter=model.dim/2,data=data_1,cur=22,renwu=model.gen_min_x)
result = pd.DataFrame(result)
result.to_excel('附件 1 的结果.xlsx')
model = GWO(maxiter=400)
best_x,best_y = model.run(data_2)
plt.plot(model.gen_best_y)
plt.show()
result, outputLine, fanNunber,costTime=model.genX(maxiter=model.dim/2,data=data_1,cur=22,renwu=model.gen_min_x)
result = pd.DataFrame(result)
result.to_excel('附件 2 的结果.xlsx')

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可