【数据结构-二叉树】二叉树

欢迎来到我的博客，很高兴能够在这里和您见面！希望您在这里可以感受到一份轻松愉快的氛围，不仅可以获得有趣的内容和知识，也可以畅所欲言、分享您的想法和见解。

• 推荐:kuan 的首页,持续学习,不断总结,共同进步,活到老学到老
• 导航
  • 檀越剑指大厂系列:全面总结 java 核心技术点,如集合,jvm,并发编程 redis,kafka,Spring,微服务,Netty 等
  • 常用开发工具系列:罗列常用的开发工具,如 IDEA,Mac,Alfred,electerm,Git,typora,apifox 等
  • 数据库系列:详细总结了常用数据库 mysql 技术点,以及工作中遇到的 mysql 问题等
  • 懒人运维系列:总结好用的命令,解放双手不香吗?能用一个命令完成绝不用两个操作
  • 数据结构与算法系列:总结数据结构和算法,不同类型针对性训练,提升编程思维,剑指大厂

非常期待和您一起在这个小小的网络世界里共同探索、学习和成长。 ✨✨ 欢迎订阅本专栏 ✨✨

一.二叉树简介

1.什么是二叉树?

二叉树是一种常见的树状数据结构，它由节点组成，每个节点最多有两个子节点，分别称为左子节点和右子节点。每个节点包含一个值或数据项，这些节点通过边（通常称为链接或指针）相互连接起来，形成一个层次结构。

2.二叉树的性质?

二叉树的特点包括：

• 根节点：二叉树的顶部节点称为根节点，它是树的起始点，没有父节点。

• 子节点：每个节点可以有零个、一个或两个子节点，分别是左子节点和右子节点。

• 叶节点：没有子节点的节点称为叶节点，它们位于树的末端。

• 高度：树的高度是从根节点到最深叶节点的最长路径的长度。

• 深度：节点的深度是从根节点到该节点的路径长度。

3.二叉树的种类

二叉树有多种不同的种类，它们在树的结构和性质上具有不同的特点。以下是一些常见的二叉树种类：

1. 二叉搜索树（Binary Search Tree，BST）：BST 是一种二叉树，其中每个节点的左子树包含的值都小于该节点的值，右子树包含的值都大于该节点的值。BST 的特性使得它非常适合用于搜索和排序操作。

2. 平衡二叉树（Balanced Binary Tree）：平衡二叉树是一种二叉搜索树，它确保树的高度平衡，从而保持搜索、插入和删除操作的平均时间复杂度为 O(log n)。

3. 完全二叉树（Complete Binary Tree）：完全二叉树是一种二叉树，除了最后一层，所有层都是完全填充的，而且最后一层的节点从左到右填充，不留空缺。这种树在堆数据结构中常常用于实现。

4. 满二叉树（Full Binary Tree）：满二叉树是一种二叉树，每个节点要么没有子节点，要么有两个子节点。所有叶子节点都在同一层上。

5. 完美二叉树（Perfect Binary Tree）：完美二叉树是一种满二叉树，它的所有叶子节点都在同一层，并且每个非叶子节点都有两个子节点。

6. 二叉堆（Binary Heap）：二叉堆是一种特殊的完全二叉树，分为最小堆和最大堆。在最小堆中，每个节点的值都小于或等于其子节点的值；在最大堆中，每个节点的值都大于或等于其子节点的值。堆通常用于实现优先队列等数据结构。

7. 线索二叉树（Threaded Binary Tree）：线索二叉树是一种特殊的二叉树，其中节点的指针指向其前驱和后继节点，这样可以实现更高效的中序遍历。

8. AVL 树：AVL 树是一种自平衡的二叉搜索树，确保树的高度平衡，从而保持插入和删除操作的时间复杂度为 O(log n)。

这些是二叉树的一些常见种类，每种类型都具有不同的特性，适用于不同的应用场景和问题。根据具体需求，选择合适的二叉树类型可以提高算法和数据结构的效率。

4.父子节点存储

存储规则分为两点:

• 定义树节点与左、右孩子引用（TreeNode）

• 使用数组，前面讲堆时用过，若以 0 作为树的根，索引可以通过如下方式计算

  • 父 = floor((子 - 1) / 2)

  • 左孩子 = 父 * 2 + 1

  • 右孩子 = 父 * 2 + 2

二.二叉树的遍历

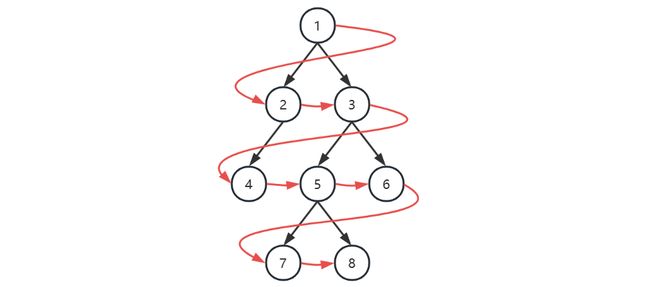
1.二叉树遍历方式

遍历也分为两种

1. 广度优先遍历（Breadth-first order）：尽可能先访问距离根最近的节点，也称为层序遍历
2. 深度优先遍历（Depth-first order）：对于二叉树，可以进一步分成三种（要深入到叶子节点）
   1. pre-order 前序遍历，对于每一棵子树，先访问该节点，然后是左子树，最后是右子树
   2. in-order 中序遍历，对于每一棵子树，先访问左子树，然后是该节点，最后是右子树
   3. post-order 后序遍历，对于每一棵子树，先访问左子树，然后是右子树，最后是该节点

2.广度优先

本轮开始时队列	本轮访问节点
[1]	1
[2, 3]	2
[3, 4]	3
[4, 5, 6]	4
[5, 6]	5
[6, 7, 8]	6
[7, 8]	7
[8]	8
[]

1. 初始化，将根节点加入队列
2. 循环处理队列中每个节点，直至队列为空
3. 每次循环内处理节点后，将它的孩子节点（即下一层的节点）加入队列

注意

• 以上用队列来层序遍历是针对 TreeNode 这种方式表示的二叉树

• 对于数组表现的二叉树，则直接遍历数组即可，自然为层序遍历的顺序

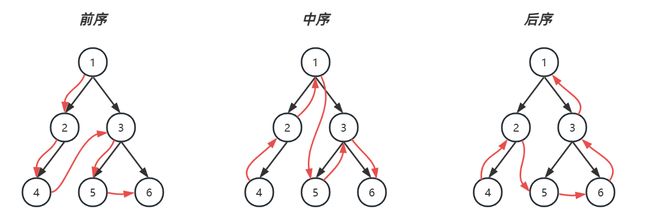
3.深度优先

栈暂存	已处理	前序遍历	中序遍历
[1]	1 ✔️ 左 右	1
[1, 2]	2✔️ 左 右 1✔️ 左 右	2
[1, 2, 4]	4✔️ 左 ✔️ 右 ✔️ 2✔️ 左 右 1✔️ 左 右	4	4
[1, 2]	2✔️ 左 ✔️ 右 ✔️ 1✔️ 左 右		2
[1]	1✔️ 左 ✔️ 右		1
[1, 3]	3✔️ 左 右 1✔️ 左 ✔️ 右	3
[1, 3, 5]	5✔️ 左 ✔️ 右 ✔️ 3✔️ 左 右 1✔️ 左 ✔️ 右	5	5
[1, 3]	3✔️ 左 ✔️ 右 1✔️ 左 ✔️ 右		3
[1, 3, 6]	6✔️ 左 ✔️ 右 ✔️ 3✔️ 左 ✔️ 右 1✔️ 左 ✔️ 右	6	6
[1, 3]	3✔️ 左 ✔️ 右 ✔️ 1✔️ 左 ✔️ 右
[1]	1✔️ 左 ✔️ 右 ✔️
[]

4.递归实现

/**
 * 
前序遍历
 * @param node 节点
 */
static void preOrder(TreeNode node) {
    if (node == null) {
        return;
    }
    System.out.print(node.val + "\t"); // 值
    preOrder(node.left); // 左
    preOrder(node.right); // 右
}

/**
 * 
中序遍历
 * @param node 节点
 */
static void inOrder(TreeNode node) {
    if (node == null) {
        return;
    }
    inOrder(node.left); // 左
    System.out.print(node.val + "\t"); // 值
    inOrder(node.right); // 右
}

/**
 * 
后序遍历
 * @param node 节点
 */
static void postOrder(TreeNode node) {
    if (node == null) {
        return;
    }
    postOrder(node.left); // 左
    postOrder(node.right); // 右
    System.out.print(node.val + "\t"); // 值
}

5.非递归实现

前序遍历

LinkedListStack<TreeNode> stack = new LinkedListStack<>();
TreeNode curr = root;

while (!stack.isEmpty() || curr != null) {
    if (curr != null) {
        stack.push(curr);
        System.out.println(curr);
        curr = curr.left;
    } else {
        TreeNode pop = stack.pop();
        curr = pop.right;
    }

}

中序遍历

LinkedListStack<TreeNode> stack = new LinkedListStack<>();
TreeNode curr = root;

while (!stack.isEmpty() || curr != null) {
    if (curr != null) {
        stack.push(curr);
        curr = curr.left;
    } else {
        TreeNode pop = stack.pop();
        System.out.println(pop);
        curr = pop.right;
    }
}

后序遍历

LinkedListStack<TreeNode> stack = new LinkedListStack<>();
TreeNode curr = root;
TreeNode pop = null;

while (!stack.isEmpty() || curr != null) {
    if (curr != null) {
        stack.push(curr);
        curr = curr.left;
    } else {
        TreeNode peek = stack.peek();
        if (peek.right == null || peek.right == pop) {
            pop = stack.pop();
            System.out.println(pop);
        } else {
            curr = peek.right;
        }
    }
}

对于后序遍历，向回走时，需要处理完右子树才能 pop 出栈。如何知道右子树处理完成呢？

• 如果栈顶元素的 $right\equiv null$ 表示没啥可处理的，可以出栈

• 如果栈顶元素的 $right\ne null$，

  • 那么使用 lastPop 记录最近出栈的节点，即表示从这个节点向回走
  • 如果栈顶元素的 $right==lastPop$ 此时应当出栈

对于前、中两种遍历，实际以上代码从右子树向回走时，并未走完全程（stack 提前出栈了）后序遍历以上代码是走完全程了

6.统一写法

下面是一种统一的写法，依据后序遍历修改

LinkedList<TreeNode> stack = new LinkedList<>();

TreeNode curr = root; // 代表当前节点
TreeNode pop = null; // 最近一次弹栈的元素
while (curr != null || !stack.isEmpty()) {
    if (curr != null) {
        colorPrintln("前: " + curr.val, 31);
        stack.push(curr); // 压入栈，为了记住回来的路
        curr = curr.left;
    } else {
        TreeNode peek = stack.peek();
        // 右子树可以不处理, 对中序来说, 要在右子树处理之前打印
        if (peek.right == null) {
            colorPrintln("中: " + peek.val, 36);
            pop = stack.pop();
            colorPrintln("后: " + pop.val, 34);
        }
        // 右子树处理完成, 对中序来说, 无需打印
        else if (peek.right == pop) {
            pop = stack.pop();
            colorPrintln("后: " + pop.val, 34);
        }
        // 右子树待处理, 对中序来说, 要在右子树处理之前打印
        else {
            colorPrintln("中: " + peek.val, 36);
            curr = peek.right;
        }
    }
}

public static void colorPrintln(String origin, int color) {
    System.out.printf("\033[%dm%s\033[0m%n", color, origin);
}

三.二叉树题目

1.对称二叉树-力扣 101 题

public boolean isSymmetric(TreeNode root) {
    return check(root.left, root.right);
}

public boolean check(TreeNode left, TreeNode right) {
    // 若同时为 null
    if (left == null && right == null) {
        return true;
    }
    // 若有一个为 null (有上一轮筛选，另一个肯定不为 null)
    if (left == null || right == null) {
        return false;
    }
    if (left.val != right.val) {
        return false;
    }
    return check(left.left, right.right) && check(left.right, right.left);
}

类似题目：Leetcode 100 题 - 相同的树

2.二叉树最大深度-力扣 104 题

后序遍历求解

/*
    思路：
    1. 得到左子树深度, 得到右子树深度, 二者最大者加一, 就是本节点深度
    2. 因为需要先得到左右子树深度, 很显然是后序遍历典型应用
    3. 关于深度的定义：从根出发, 离根最远的节点总边数,
        注意: 力扣里的深度定义要多一

        深度2         深度3         深度1
        1            1            1
       / \          / \
      2   3        2   3
                        \
                         4
 */
public int maxDepth(TreeNode node) {
    if (node == null) {
        return 0; // 非力扣题目改为返回 -1
    }
    int d1 = maxDepth(node.left);
    int d2 = maxDepth(node.right);
    return Integer.max(d1, d2) + 1;
}

后序遍历求解-非递归

/*
    思路：
    1. 使用非递归后序遍历, 栈的最大高度即为最大深度
 */
public int maxDepth(TreeNode root) {
    TreeNode curr = root;
    LinkedList<TreeNode> stack = new LinkedList<>();
    int max = 0;
    TreeNode pop = null;
    while (curr != null || !stack.isEmpty()) {
        if (curr != null) {
            stack.push(curr);
            int size = stack.size();
            if (size > max) {
                max = size;
            }
            curr = curr.left;
        } else {
            TreeNode peek = stack.peek();
            if(peek.right == null || peek.right == pop) {
                pop = stack.pop();
            } else {
                curr = peek.right;
            }
        }
    }
    return max;
}

层序遍历求解

/*
    思路：
    1. 使用层序遍历, 层数即最大深度
 */
public int maxDepth(TreeNode root) {
    if(root == null) {
        return 0;
    }
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    int level = 0;
    while (!queue.isEmpty()) {
        level++;
        int size = queue.size();
        for (int i = 0; i < size; i++) {
            TreeNode node = queue.poll();
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
    }
    return level;
}

3.二叉树最小深度-力扣 111 题

后序遍历求解

public int minDepth(TreeNode node) {
    if (node == null) {
        return 0;
    }
    int d1 = minDepth(node.left);
    int d2 = minDepth(node.right);
    if (d1 == 0 || d2 == 0) {
        return d1 + d2 + 1;
    }
    return Integer.min(d1, d2) + 1;
}

相较于求最大深度，应当考虑：

• 当右子树为 null，应当返回左子树深度加一
• 当左子树为 null，应当返回右子树深度加一

上面两种情况满足时，不应该再把为 null 子树的深度 0 参与最小值比较，例如这样

    1
   /
  2

• 正确深度为 2，若把为 null 的右子树的深度 0 考虑进来，会得到错误结果 1

    1
     \
      3
       \
        4

• 正确深度为 3，若把为 null 的左子树的深度 0 考虑进来，会得到错误结果 1

层序遍历求解

遇到的第一个叶子节点所在层就是最小深度

例如，下面的树遇到的第一个叶子节点 3 所在的层就是最小深度，其他 4，7 等叶子节点深度更深，也更晚遇到

     1
    / \
   2   3
  / \
 4   5
    /
   7

代码

public int minDepth(TreeNode root) {
    if(root == null) {
        return 0;
    }
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    int level = 0;
    while (!queue.isEmpty()) {
        level++;
        int size = queue.size();
        for (int i = 0; i < size; i++) {
            TreeNode node = queue.poll();
            if (node.left == null && node.right == null) {
                return level;
            }
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
    }
    return level;
}

效率会高于之前后序遍历解法，因为找到第一个叶子节点后，就无需后续的层序遍历了

4.翻转二叉树-力扣 226 题

public TreeNode invertTree(TreeNode root) {
    fn(root);
    return root;
}

private void fn(TreeNode node){
    if (node == null) {
        return;
    }
    TreeNode t = node.left;
    node.left = node.right;
    node.right = t;
    fn(node.left);
    fn(node.right);
}

先交换、再递归或是先递归、再交换都可以

5.后缀表达式转二叉树

static class TreeNode {
    public String val;
    public TreeNode left;
    public TreeNode right;

    public TreeNode(String val) {
        this.val = val;
    }

    public TreeNode(TreeNode left, String val, TreeNode right) {
        this.left = left;
        this.val = val;
        this.right = right;
    }

    @Override
    public String toString() {
        return this.val;
    }
}

/*
    中缀表达式           (2-1)*3
    后缀（逆波兰）表达式   21-3*

    1.遇到数字入栈
    2.遇到运算符, 出栈两次, 与当前节点建立父子关系, 当前节点入栈

    栈
    |   |
    |   |
    |   |
    _____

    表达式树
        *
       / \
      -   3
     / \
    2   1

    21-3*
 */
public TreeNode constructExpressionTree(String[] tokens) {
    LinkedList<TreeNode> stack = new LinkedList<>();
    for (String t : tokens) {
        switch (t) {
            case "+", "-", "*", "/" -> { // 运算符
                TreeNode right = stack.pop();
                TreeNode left = stack.pop();
                TreeNode parent = new TreeNode(t);
                parent.left = left;
                parent.right = right;
                stack.push(parent);
            }
            default -> { // 数字
                stack.push(new TreeNode(t));
            }
        }
    }
    return stack.peek();
}

6.根据前序与中序遍历结果构造二叉树-力扣 105 题

• 先通过前序遍历结果定位根节点
• 再结合中序遍历结果切分左右子树

public class E09Leetcode105 {

    /*
        preOrder = {1,2,4,3,6,7}
        inOrder = {4,2,1,6,3,7}

        根 1
            pre         in
        左  2,4         4,2
        右  3,6,7       6,3,7


        根 2
        左 4

        根 3
        左 6
        右 7
     */

    public TreeNode buildTree(int[] preOrder, int[] inOrder) {
        if (preOrder.length == 0) {
            return null;
        }
        // 创建根节点
        int rootValue = preOrder[0];
        TreeNode root = new TreeNode(rootValue);
        // 区分左右子树
        for (int i = 0; i < inOrder.length; i++) {
            if (inOrder[i] == rootValue) {
                // 0 ~ i-1 左子树
                // i+1 ~ inOrder.length -1 右子树
                int[] inLeft = Arrays.copyOfRange(inOrder, 0, i); // [4,2]
                int[] inRight = Arrays.copyOfRange(inOrder, i + 1, inOrder.length); // [6,3,7]

                int[] preLeft = Arrays.copyOfRange(preOrder, 1, i + 1); // [2,4]
                int[] preRight = Arrays.copyOfRange(preOrder, i + 1, inOrder.length); // [3,6,7]

                root.left = buildTree(preLeft, inLeft); // 2
                root.right = buildTree(preRight, inRight); // 3
                break;
            }
        }
        return root;
    }

}

• 代码可以进一步优化，涉及新数据结构，以后实现

7.根据中序与后序遍历结果构造二叉树-力扣 106 题

• 先通过后序遍历结果定位根节点
• 再结合中序遍历结果切分左右子树

public TreeNode buildTree(int[] inOrder, int[] postOrder) {
    if (inOrder.length == 0) {
        return null;
    }
    // 根
    int rootValue = postOrder[postOrder.length - 1];
    TreeNode root = new TreeNode(rootValue);
    // 切分左右子树
    for (int i = 0; i < inOrder.length; i++) {
        if (inOrder[i] == rootValue) {
            int[] inLeft = Arrays.copyOfRange(inOrder, 0, i);
            int[] inRight = Arrays.copyOfRange(inOrder, i + 1, inOrder.length);

            int[] postLeft = Arrays.copyOfRange(postOrder, 0, i);
            int[] postRight = Arrays.copyOfRange(postOrder, i, postOrder.length - 1);

            root.left = buildTree(inLeft, postLeft);
            root.right = buildTree(inRight, postRight);
            break;
        }
    }
    return root;
}

• 代码可以进一步优化，涉及新数据结构，以后实现

觉得有用的话点个赞 呗。
❤️❤️❤️本人水平有限，如有纰漏，欢迎各位大佬评论批评指正！

如果觉得这篇文对你有帮助的话，也请给个点赞、收藏下吧，非常感谢!

Stay Hungry Stay Foolish 道阻且长,行则将至,让我们一起加油吧！