Day27|leetcode 39. 组合总和、40.组合总和II、131.分割回文串

leetcode 39. 组合总和

题目链接：39. 组合总和 - 力扣（LeetCode）

视频链接：带你学透回溯算法-组合总和（对应「leetcode」力扣题目：39.组合总和）| 回溯法精讲！_哔哩哔哩_bilibili

题目概述

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。 

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

思路

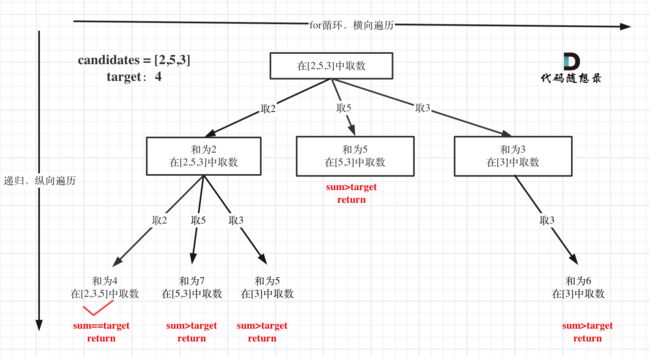
本题对数量没有要求，可以无限重复，而且给的数组是无重复的，这样就可以不用考虑去重操作了。过程如下：

 因为对数字重复没有要求，所以在第一层for循环时，取2后，还剩[2，3，5]而不是像上两题一样，取2后，就剩[3，5]了，这需要注意一下。

本题依旧使用startindex，为什么使用startindex而不使用index呢，因为这是在一个集合里，所以说：在一个集合里取组合用startindex，在多个不同的集合里取组合用index。

代码实现

class Solution {
public:
    vector> combinationSum(vector& candidates, int target) {
        sort(candidates.begin(),candidates.end());
        backtracking(candidates,target,0,0);
        return result;
    }
private:
    vector> result;
    vector path;
    void backtracking(vector& candidates,int target,int sum,int startIndex) {
        if(sum == target) {
            result.push_back(path);
            return;
        }
        for(int i = startIndex;i < candidates.size() && sum + candidates[i] <= target;i++) {
            sum += candidates[i];
            path.push_back(candidates[i]);
            backtracking(candidates,target,sum,i);
            sum -= candidates[i];
            path.pop_back();
        }
    }
};

剪枝优化

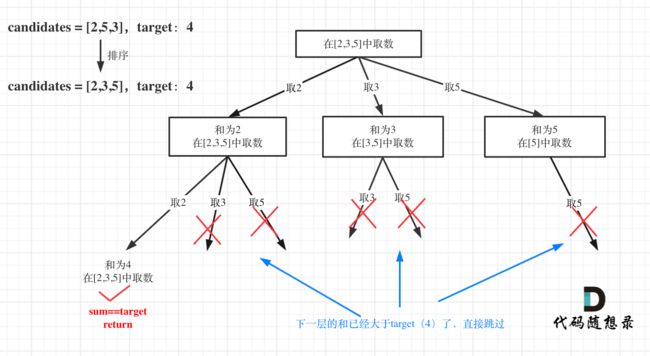
本题也可以剪枝优化，只不过需要提前把数组给排一下序。过程如图所示：

只要确定和大于目标值了，就返回，不用继续往后遍历了。

代码实现：

class Solution {
private:
    vector> result;
    vector path;
    void backtracking(vector& candidates, int target, int sum, int startIndex) {
        if (sum == target) {
            result.push_back(path);
            return;
        }

        // 如果 sum + candidates[i] > target 就终止遍历
        for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
            sum += candidates[i];
            path.push_back(candidates[i]);
            backtracking(candidates, target, sum, i);
            sum -= candidates[i];
            path.pop_back();

        }
    }
public:
    vector> combinationSum(vector& candidates, int target) {
        result.clear();
        path.clear();
        sort(candidates.begin(), candidates.end()); // 需要排序
        backtracking(candidates, target, 0, 0);
        return result;
    }
};

在求和问题中，排序之后加剪枝是常见的套路！

leetcode 40.组合总和II

题目链接：40. 组合总和 II - 力扣（LeetCode）

视频链接：回溯算法中的去重，树层去重树枝去重，你弄清楚了没？| LeetCode:40.组合总和II_哔哩哔哩_bilibili

题目概述

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

注意：解集不能包含重复的组合。 

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

思路

本题所给数组里的元素可以重复，但是要求的集合却不能重复，这里就要考虑去重问题了。就拿示例一举例，target=8，除了[1，7][7，1]，它俩的值加起来都为8，集合里的元素也一样，因为集合是无序的，不讲究排序问题，所以说它两重了，所以要考虑去重问题。

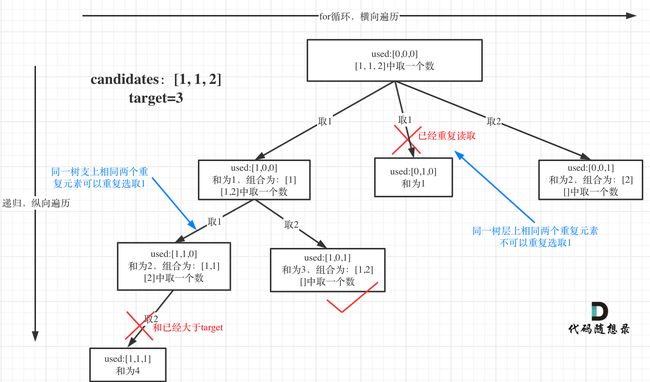
去重以前我们应该把序排好了，而去重我们应该去的是同一层上的重，因为去重，其实就是使用过的元素不能重复选取，如图所示：

 去同层上的重的原因就是，如果你去了同枝上的重，就有可能遗漏一些符合要求的情况，而且在去重之前已经排好序了，就说明在给定的集合里，如果有和前面一样的数字，那么如果在遍历相同的数字的时候，第一次的情况肯定包含和第二次相同的情况，所以要同层去重。

代码实现

class Solution {
public:
    vector> combinationSum2(vector& candidates, int target) {
        vector used(candidates.size(), false);
        path.clear();
        result.clear();
        // 首先把给candidates排序，让其相同的元素都挨在一起。
        sort(candidates.begin(), candidates.end());
        backtracking(candidates, target, 0, 0, used);
        return result;
    }

private:
    vector> result;
    vector path;
    void backtracking(vector& candidates, int target, int sum, int startIndex, vector& used) {
        if (sum == target) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
            // used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
            // used[i - 1] == false，说明同一树层candidates[i - 1]使用过
            // 要对同一树层使用过的元素进行跳过
            if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
                continue;
            }
            sum += candidates[i];
            path.push_back(candidates[i]);
            used[i] = true;
            backtracking(candidates, target, sum, i + 1, used); // 和39.组合总和的区别1，这里是i+1，每个数字在每个组合中只能使用一次
            used[i] = false;
            sum -= candidates[i];
            path.pop_back();
        }
    }


};

leetcode 131.分割回文串

题目链接：131. 分割回文串 - 力扣（LeetCode）

视频链接：带你学透回溯算法-分割回文串（对应力扣题目：131.分割回文串）| 回溯法精讲！_哔哩哔哩_bilibili

题目概述

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

回文串 是正着读和反着读都一样的字符串。

示例 1：

输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

思路

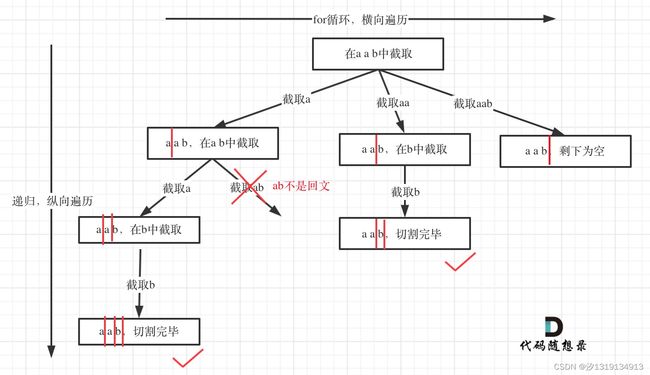
切割问题的回溯搜索的过程和组合问题的回溯搜索的过程是差不多的，如图所示：

这里的红切割线就是startIndex，它表示下一轮切割的起始位置。 

 判断是否是回文子串，就用双指针法，一个从前往后，一个从后往前，如果所指元素相等，那就是回文子串了。

代码实现

class Solution {
public:
    vector> partition(string s) {
        result.clear();
        path.clear();
        backtracking(s, 0);
        return result;
    }

private:
    vector> result;
    vector path; // 放已经回文的子串
    void backtracking (const string& s, int startIndex) {
        // 如果起始位置已经大于s的大小，说明已经找到了一组分割方案了
        if (startIndex >= s.size()) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i < s.size(); i++) {
            if (isPalindrome(s, startIndex, i)) {   // 是回文子串
                // 获取[startIndex,i]在s中的子串
                string str = s.substr(startIndex, i - startIndex + 1);
                path.push_back(str);
            } else {                                // 不是回文，跳过
                continue;
            }
            backtracking(s, i + 1); // 寻找i+1为起始位置的子串
            path.pop_back(); // 回溯过程，弹出本次已经添加的子串
        }
    }
    bool isPalindrome(const string& s, int start, int end) {
        for (int i = start, j = end; i < j; i++, j--) {
            if (s[i] != s[j]) {
                return false;
            }
        }
        return true;
    }
};