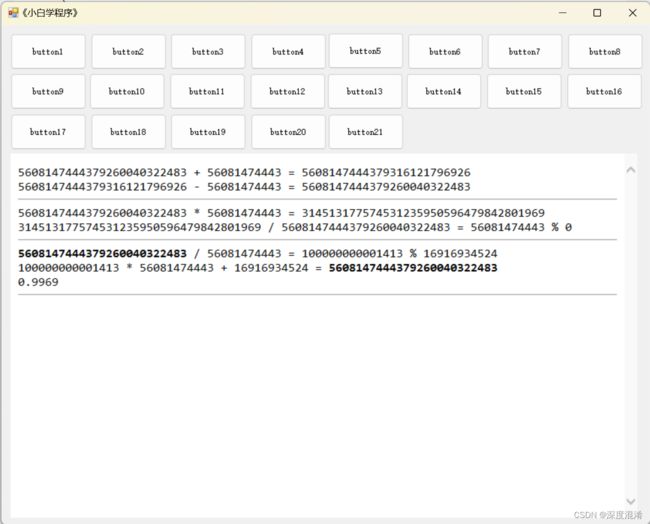
C#,《小白学程序》第二十一课:大数(BigInteger)的四则运算之二,减法
1 文本格式
using System;
using System.Linq;
using System.Text;
using System.Collections.Generic;
///
/// 大数的(加减乘除)四则运算、阶乘运算
/// 乘法计算包括小学生算法、Karatsuba和Toom-Cook3算法
///
public static class BigInteger_Utility
{
///
/// 记录 加减乘除 的运算次数
///
public static int[] operations { get; set; } = new int[] { 0, 0, 0, 0 };
///
/// 《小白学程序》第十九课:随机数(Random)第六,随机生成任意长度的大数(BigInteger)
/// 一般可将超过9位数的数字成为“大数”。
/// 两个大数之间的四则运算用于密码学、高精度计算等应用。
/// 位数很多的浮点数可转为大数,再逆转即可。
///
///
///
public static string rand(int n)
{
// 随机数发生器
Random rnd = new Random();
StringBuilder sb = new StringBuilder();
// 第一个数字不能为0,故:0-8之间的随机数+ 1 = 1-9
sb.Append((rnd.Next(9) + 1).ToString());
// 后面 n-1 个数字为 0-9;从 1 开始计数
for (int i = 1; i < n; i++)
{
sb.Append((rnd.Next(10)).ToString());
}
return sb.ToString();
}
///
/// 字符串型的数字转为数组
/// 低位(右)在前,比如 "123" , n=6 存为 3,2,1,_,_,_
/// n 可能大于 a 的长度;剩余位置留出来用于 进位 等。
///
///
/// 最大位数,后面留0
///
public static int[] string_to_digitals(string a, int n)
{
// 字符串 转为 “字符数组”
char[] c = a.ToCharArray();
// 存储数字的数组
int[] d = new int[n];
// 从最右端(个位)数字开始,转存为数字数组,参与后面的计算
for (int i = a.Length - 1, j = 0; i >= 0; i--)
{
// 跳过数字前面可能有的 - 号
if (a[i] == '-') continue;
// '0' 字符是最小的数字字符
// 数值 = 字符 - '0' ;
d[j++] = a[i] - '0';
}
return d;
}
///
/// 数组型数字转为字符串型
/// 低位(右)在前,比如 3,2,1,_,_,_ 转为 "123", n=6
/// 这是前面 string_to_digitals 的反向计算函数
/// n 可能大于 d 的长度;剩余位置留出来用于 进位 等。
///
///
///
public static string digitals_to_string(int[] d)
{
int n = d.Length;
// 数字数组 d 含有一些无效的数组;
// 因此,先从最右段开始去除无效的位置
int k = n - 1;
//for (; (k >= 0) && (d[k] == 0); k--) ;
while ((k >= 0) && (d[k] == 0)) k--;
// 找到有效位置后,开始组合字符串;
if (k >= 0)
{
StringBuilder sb = new StringBuilder();
for (; k >= 0; k--) sb.Append(d[k]);
return sb.ToString();
}
else
{
return "0";
}
}
///
/// 《小白学程序》第二十一课:大数(BigInteger)的四则运算之二,减法
/// 大数减法 c = a - b
///
///
///
///
public static string big_integer_subtract(string a, string b)
{
int na = a.Length;
int nb = b.Length;
int n = Math.Max(na, nb) + 1;
// 位数不长的数字直接计算
if (n <= 18)
{
return (ulong.Parse(a) - ulong.Parse(b)).ToString();
}
int[] da = string_to_digitals(a, n);
int[] db = string_to_digitals(b, n);
if (na > nb ||
((na == nb) && big_integer_compare(da, db) >= 0))
{
// 从低位(右)往高位(左)相减
for (int i = 0; i < na; i++)
{
da[i] -= db[i];
if (da[i] < 0)
{
da[i] += 10;
da[i + 1] -= 1;
}
}
return digitals_to_string(da);
}
else
{
for (int i = 0; i < nb; i++)
{
db[i] -= da[i];
if (db[i] < 0)
{
db[i] += 10;
db[i + 1] -= 1;
}
}
string r = digitals_to_string(db);
return (r == "0") ? r : "-" + r;
}
}
}
2 代码格式
using System;
using System.Linq;
using System.Text;
using System.Collections.Generic;
///
/// 大数的(加减乘除)四则运算、阶乘运算
/// 乘法计算包括小学生算法、Karatsuba和Toom-Cook3算法
///
public static class BigInteger_Utility
{
///
/// 记录 加减乘除 的运算次数
///
public static int[] operations { get; set; } = new int[] { 0, 0, 0, 0 };
///
/// 《小白学程序》第十九课:随机数(Random)第六,随机生成任意长度的大数(BigInteger)
/// 一般可将超过9位数的数字成为“大数”。
/// 两个大数之间的四则运算用于密码学、高精度计算等应用。
/// 位数很多的浮点数可转为大数,再逆转即可。
///
///
///
/// 字符串型的数字转为数组
/// 低位(右)在前,比如 "123" , n=6 存为 3,2,1,_,_,_
/// n 可能大于 a 的长度;剩余位置留出来用于 进位 等。
///
///
/// 最大位数,后面留0
///
/// 数组型数字转为字符串型
/// 低位(右)在前,比如 3,2,1,_,_,_ 转为 "123", n=6
/// 这是前面 string_to_digitals 的反向计算函数
/// n 可能大于 d 的长度;剩余位置留出来用于 进位 等。
///
///
///
/// 《小白学程序》第二十一课:大数(BigInteger)的四则运算之二,减法
/// 大数减法 c = a - b
///
///
///
///