DenseNet论文翻译精读

DenseNet论文翻译精读

Densely Connected Convolutional Networks

论文在线阅读：https://ieeexplore.ieee.org/document/8099726

Abstract

Recent work has shown that convolutional networks can be substantially deeper, more accurate, and efficient to train if they contain shorter connections between layers close to the input and those close to the output. In this paper, we embrace this observation and introduce the Dense Convolutional Network (DenseNet), which connects each layer to every other layer in a feed-forward fashion. Whereas traditional convolutional networks with L layers have L connections-one between each layer and its subsequent layer-our network has L(L+1)/2 direct connections. For each layer, the feature-maps of all preceding layers are used as inputs, and its own feature-maps are used as inputs into all subsequent layers. DenseNets have several compelling advantages: they alleviate the vanishing-gradient problem, strengthen feature propagation, encourage feature reuse, and substantially reduce the number of parameters. We evaluate our proposed architecture on four highly competitive object recognition benchmark tasks (CIFAR-10, CIFAR-100, SVHN, and ImageNet). DenseNets obtain significant improvements over the state-of-the-art on most of them, whilst requiring less memory and computation to achieve high performance. Code and pre-trained models are available at https://github.com/liuzhuang13/DenseNet.
最近的研究表明，如果卷积网络在靠近输入的层和靠近输出的层之间包含较短的连接，那么它们的训练可以更深、更准确、更高效。在本文中，我们接受了这一观察并介绍了密集卷积网络（DenseNet），它以前馈方式将每一层与其他每一层连接起来。而具有 L 层的传统卷积网络有 L 个连接（每层与其后续层之间有一个连接），而我们的网络有 L(L+1)/2 个直接连接。对于每一层，所有先前层的特征图用作输入，并且其自己的特征图用作所有后续层的输入。 DenseNet 有几个引人注目的优点：它们缓解了梯度消失问题，加强了特征传播，鼓励特征重用，并大幅减少了参数数量。我们在四个高度竞争的对象识别基准任务（CIFAR-10、CIFAR-100、SVHN 和 ImageNet）上评估了我们提出的架构。 DenseNets 比大多数最先进的网络获得了显着的改进，同时需要更少的内存和计算来实现高性能。代码和预训练模型可在 https://github.com/liuzhuang13/DenseNet 获取。

SECTION 1.Introduction

Convolutional neural networks (CNNs) have become the dominant machine learning approach for visual object recognition. Although they were originally introduced over 20 years ago [18], improvements in computer hardware and network structure have enabled the training of truly deep CNNs only recently. The original LeNet5 [19] consisted of 5 layers, VGG featured 19 [28], and only last year Highway Networks [33] and Residual Networks (ResNets) [11] have surpassed the 100-layer barrier.
卷积神经网络（CNN）已成为视觉对象识别的主要机器学习方法。尽管它们最初是在 20 多年前引入的[18]，但直到最近计算机硬件和网络结构的改进才使得真正的深度 CNN 的训练成为可能。最初的 LeNet5 [19] 由 5 层组成，VGG 有 19 层 [28]，直到去年 Highway Networks [33] 和 Residual Networks (ResNets) [11] 才突破了 100 层的障碍。

Figure 1:A 5-layer dense block with a growth rate of k=4. Each layer takes all preceding feature-maps as input. 图 1：增长率为 k=4 的 5 层致密块。每一层都将所有前面的特征图作为输入。

As CNNs become increasingly deep, a new research problem emerges: as information about the input or gradient passes through many layers, it can vanish and “wash out” by the time it reaches the end (or beginning) of the network. Many recent publications address this or related problems. ResNets [11] and Highway Networks [33] bypass signal from one layer to the next via identity connections. Stochastic depth [13] shortens ResNets by randomly dropping layers during training to allow better information and gradient flow. FractalNets [17] repeatedly combine several parallel layer sequences with different number of convolutional blocks to obtain a large nominal depth, while maintaining many short paths in the network. Although these different approaches vary in network topology and training procedure, they all share a key characteristic: they create short paths from early layers to later layers.
随着 CNN 变得越来越深，一个新的研究问题出现了：当有关输入或梯度的信息经过许多层时，当它到达网络的末端（或开始）时，它可能会消失并“被冲走”。最近的许多出版文章都解决了这个问题或相关问题。 ResNets [11] 和 Highway Networks [33] 通过等值连接将信号从一层旁路到下一层。随机深度 [13] 通过在训练期间随机丢弃层来缩短 ResNet，以允许更好的信息和梯度流。 FractalNets [17]将多个并行层序列与不同数量的卷积块重复组合以获得大的标称深度，同时在网络中保持许多短路径。尽管这些不同的方法在网络拓扑和训练过程上有所不同，但它们都有一个关键特征：它们创建从早期层到后面层的短路径。

In this paper, we propose an architecture that distills this insight into a simple connectivity pattern: to ensure maximum information flow between layers in the network, we connect all layers (with matching feature-map sizes) directly with each other. To preserve the feed-forward nature, each layer obtains additional inputs from all preceding layers and passes on its own feature-maps to all subsequent layers. Figure 1 illustrates this layout schematically. Crucially, in contrast to ResNets, we never combine features through summation before they are passed into a layer; instead, we combine features by concatenating them. Hence, the ℓth layer has ℓ inputs, consisting of the feature-maps of all preceding convolutional blocks. Its own feature-maps are passed on to all L−ℓ subsequent layers. This introduces L(L+1)2 connections in an L-layer network, instead of just L, as in traditional architectures. Because of its dense connectivity pattern, we refer to our approach as Dense Convolutional Network (DenseNet).
在本文中，我们提出了一种架构，将这种见解提炼为简单的连接模式：为了确保网络中各层之间的最大信息流，我们将所有层（具有匹配的特征图大小）直接相互连接。为了保持前馈性质，每个层从所有前面的层获取额外的输入，并将其自己的特征图传递到所有后续层。图 1 示意性地说明了这种布局。至关重要的是，与 ResNet 相比，我们在将特征传递到层之前从不通过求和来组合特征；相反，我们通过连接特征来组合它们。因此，第ℓ层有ℓ个输入，由所有前面的卷积块的特征图组成。它自己的特征图被传递到所有 L−ℓ 后续层。这在 L 层网络中引入了 L(L+1)/2 个连接，而不是像传统架构中那样只有 L 个连接。由于其密集的连接模式，我们将我们的方法称为密集卷积网络（DenseNet）。

A possibly counter-intuitive effect of this dense connectivity pattern is that it requires fewer parameters than traditional convolutional networks, as there is no need to relearn redundant feature-maps. Traditional feed-forward architectures can be viewed as algorithms with a state, which is passed on from layer to layer. Each layer reads the state from its preceding layer and writes to the subsequent layer. It changes the state but also passes on information that needs to be preserved. ResNets [11] make this information preservation explicit through additive identity transformations. Recent variations of ResNets [13] show that many layers contribute very little and can in fact be randomly dropped during training. This makes the state of ResNets similar to (unrolled) recurrent neural networks [21], but the number of parameters of ResNets is substantially larger because each layer has its own weights. Our proposed DenseNet architecture explicitly differentiates between information that is added to the network and information that is preserved. DenseNet layers are very narrow (e.g., 12 filters per layer), adding only a small set of feature-maps to the “collective knowledge” of the network and keep the remaining feature-maps unchanged—and the final classifier makes a decision based on all feature-maps in the network.
这种密集连接模式的一个可能违反直觉的效果是，它比传统卷积网络需要更少的参数，因为不需要重新学习冗余特征图。传统的前馈架构可以被视为具有状态的算法，该状态从一层传递到另一层。每层从其前一层读取状态并写入后续层。它改变状态，但也传递需要保留的信息。 ResNets [11] 通过加性恒等变换使信息保存变得明确。 ResNets [13] 的最新变化表明，许多层贡献很小，实际上可以在训练过程中随机丢弃。这使得 ResNets 的状态类似于（展开的）循环神经网络 [21]，但 ResNets 的参数数量要大得多，因为每层都有自己的权重。我们提出的 DenseNet 架构明确区分添加到网络的信息和保留的信息。 DenseNet 层非常窄（例如，每层 12 个过滤器），仅将一小部分特征图添加到网络的“集体知识”中，并保持其余特征图不变，最终分类器根据网络中的所有特征图。

Besides better parameter efficiency, one big advantage of DenseNets is their improved flow of information and gradients throughout the network, which makes them easy to train. Each layer has direct access to the gradients from the loss function and the original input signal, leading to an implicit deep supervision [20]. This helps training of deeper network architectures. Further, we also observe that dense connections have a regularizing effect, which reduces overfitting on tasks with smaller training set sizes.
除了更好的参数效率之外，DenseNet 的一大优势是改善了整个网络的信息流和梯度，这使得它们易于训练。每层都可以直接访问损失函数和原始输入信号的梯度，从而产生隐式深度监督[20]。这有助于训练更深层的网络架构。此外，我们还观察到密集连接具有正则化效果，可以减少训练集较小的任务的过度拟合。

We evaluate DenseNets on four highly competitive benchmark datasets (CIFAR-10, CIFAR-100, SVHN, and ImageNet). Our models tend to require much fewer parameters than existing algorithms with comparable accuracy. Further, we significantly outperform the current state-of-the-art results on most of the benchmark tasks.
我们在四个高度竞争的基准数据集（CIFAR-10、CIFAR-100、SVHN 和 ImageNet）上评估 DenseNet。我们的模型往往需要比具有相当精度的现有算法少得多的参数。此外，我们在大多数基准任务上都显着优于当前最先进的结果。

SECTION 2.Related Work

The exploration of network architectures has been a part of neural network research since their initial discovery. The recent resurgence in popularity of neural networks has also revived this research domain. The increasing number of layers in modern networks amplifies the differences between architectures and motivates the exploration of different connectivity patterns and the revisiting of old research ideas.
自最初发现以来，对网络架构的探索一直是神经网络研究的一部分。最近神经网络的重新流行也复兴了这一研究领域。现代网络中层数的增加放大了架构之间的差异，并激发了对不同连接模式的探索和对旧研究思想的重新审视。

A cascade structure similar to our proposed dense network layout has already been studied in the neural networks literature in the 1980s [3]. Their pioneering work focuses on fully connected multi-layer perceptrons trained in a layer-by-layer fashion. More recently, fully connected cascade networks to be trained with batch gradient descent were proposed [39]. Although effective on small datasets, this approach only scales to networks with a few hundred parameters. In [9], [23], [30], [40], utilizing multi-level features in CNNs through skip-connnections has been found to be effective for various vision tasks. Parallel to our work, [1] derived a purely theoretical framework for networks with cross-layer connections similar to ours.
类似于我们提出的密集网络布局的级联结构已经在 20 世纪 80 年代的神经网络文献中进行了研究 [3]。他们的开创性工作侧重于以逐层方式训练的完全连接的多层感知器。最近，提出了用批量梯度下降训练的全连接级联网络[39]。尽管对小型数据集有效，但这种方法只能扩展到具有数百个参数的网络。在[9]、[23]、[30]、[40]中，通过跳跃连接利用 CNN 中的多级特征已被发现对各种视觉任务有效。与我们的工作并行，[1] 导出了一个纯理论框架，用于具有与我们类似的跨层连接的网络。

Highway Networks [33] were amongst the first architectures that provided a means to effectively train end-to-end networks with more than 100 layers. Using bypassing paths along with gating units, Highway Networks with hundreds of layers can be optimized without difficulty. The bypassing paths are presumed to be the key factor that eases the training of these very deep networks. This point is further supported by ResNets [11], in which pure identity mappings are used as bypassing paths. ResNets have achieved impressive, record-breaking performance on many challenging image recognition, localization, and detection tasks, such as ImageNet and COCO object detection [11]. Recently, stochastic depth was proposed as a way to successfully train a 1202-layer ResNet [13]. Stochastic depth improves the training of deep residual networks by dropping layers randomly during training. This shows that not all layers may be needed and highlights that there is a great amount of redundancy in deep (residual) networks. Our paper was partly inspired by that observation. ResNets with pre-activation also facilitate the training of state-of-the-art networks with > 1000 layers [12].
Highway Networks [33] 是最早提供有效训练 100 层以上端到端网络方法的架构之一。使用旁路路径和门控单元，可以毫无困难地优化数百层的Highway网络。旁路路径被认为是简化这些非常深的网络训练的关键因素。 ResNets [11]进一步支持了这一点，其中使用纯恒等映射作为旁路路径。 ResNets 在许多具有挑战性的图像识别、定位和检测任务上取得了令人印象深刻、破纪录的性能，例如 ImageNet 和 COCO 对象检测 [11]。最近，随机深度被提出作为成功训练 1202 层 ResNet 的一种方法[13]。随机深度通过在训练过程中随机丢弃层来改进深度残差网络的训练。这表明并非所有层都是必需的，并强调深度（残差）网络中存在大量冗余。我们的论文部分受到了这一观察的启发。具有预激活功能的 ResNet 还有助于训练超过 1000 层的最先进网络 [12]。

An orthogonal approach to making networks deeper (e.g., with the help of skip connections) is to increase the network width. The GoogLeNet [35], [36] uses an “Inception module” which concatenates feature-maps produced by filters of different sizes. In [37], a variant of ResNets with wide generalized residual blocks was proposed. In fact, simply increasing the number of filters in each layer of ResNets can improve its performance provided the depth is sufficient [41]. FractalNets also achieve competitive results on several datasets using a wide network structure [17].
使网络更深的正交方法（例如，借助跳跃连接）是增加网络宽度。 GoogLeNet [35]、[36] 使用“Inception 模块”，该模块连接由不同大小的过滤器生成的特征图。在[37]中，提出了一种具有宽广义残差块的 ResNet 变体。事实上，只要深度足够，简单地增加 ResNets 每层中的滤波器数量就可以提高其性能[41]。 FractalNets 还使用广泛的网络结构在多个数据集上取得了有竞争力的结果 [17]。

Figure 2:A deep DenseNet with three dense blocks. The layers between two adjacent blocks are referred to as transition layers and change feature-map sizes via convolution and pooling. 图 2：具有三个密集块的深度 DenseNet。两个相邻块之间的层称为过渡层，并通过卷积和池化改变特征图大小。

Instead of drawing representational power from extremely deep or wide architectures, DenseNets exploit the potential of the network throughfeature reuse, yielding condensed models that are easy to train and highly parameter-efficient. Concatenating feature-maps learned by different layers increases variation in the input of subsequent layers and improves efficiency. This constitutes a major difference between DenseNets and ResNets. Compared to Inception networks [35], [36], which also concatenate features from different layers, DenseNets are simpler and more efficient.
DenseNet 不是从极深或极宽的架构中汲取表征能力，而是通过特征重用来挖掘网络的潜力，产生易于训练且参数效率高的精简模型。连接不同层学习的特征图会增加后续层输入的变化并提高效率。这是 DenseNets 和 ResNets 之间的主要区别。与同样连接不同层特征的 Inception 网络 [35]、[36] 相比，DenseNet 更简单、更高效。

There are other notable network architecture innovations which have yielded competitive results. The Network in Network (NIN) [22] structure includes micro multi-layer perceptrons into the filters of convolutional layers to extract more complicated features. In Deeply Supervised Network (DSN) [20], internal layers are directly supervised by auxiliary classifiers, which can strengthen the gradients received by earlier layers. Ladder Networks [26], [25] introduce lateral connections into autoencoders, producing impressive accuracies on semi-supervised learning tasks. In [38], Deeply-Fused Nets (DFNs) were proposed to improve information flow by combining intermediate layers of different base networks. The augmentation of networks with pathways that minimize reconstruction losses was also shown to improve image classification models [42].
还有其他值得注意的网络架构创新也产生了有竞争力的结果。网络中的网络（NIN）[22]结构将微型多层感知器纳入卷积层的滤波器中，以提取更复杂的特征。在深度监督网络（DSN）[20]中，内部层由辅助分类器直接监督，这可以加强早期层接收到的梯度。梯形网络 [26]、[25] 将横向连接引入自动编码器，在半监督学习任务上产生令人印象深刻的准确性。在[38]中，提出了深度融合网络（DFN），通过组合不同基础网络的中间层来改善信息流。通过最小化重建损失的路径增强网络也被证明可以改进图像分类模型[42]。

SECTION 3.DenseNets

Consider a single image x0 that is passed through a convolutional network. The network comprises L layers, each of which implements a non-linear transformation Hℓ(⋅), where ℓ indexes the layer. Hℓ(⋅) can be a composite function of operations such as Batch Normalization (BN) [14], rectified linear units (ReLU) [6], Pooling [19], or Convolution (Conv). We denote the output of the ℓth layer as xℓ.
考虑通过卷积网络的单个图像 x0。该网络包含 L 层，每层都实现非线性变换 Hℓ(⋅)，其中 ℓ 对该层进行索引。 Hℓ(⋅) 可以是批量归一化 (BN) [14]、修正线性单元 (ReLU) [6]、池化 [19] 或卷积 (Conv) 等运算的复合函数。我们将第ℓ层的输出表示为xℓ。

ResNets

Traditional convolutional feed-forward networks connect the output of the ℓth layer as input to the (ℓ+1)th layer [16], which gives rise to the following layer transition: xℓ=Hℓ(xl−1). ResNets [11] add a skip-connection that bypasses the non-linear transformations with an identity function:
传统的卷积前馈网络将第ℓ层的输出作为输入连接到第(ℓ+1)层[16]，从而产生以下层转换：xℓ=Hℓ(xl−1)。 ResNets [11] 添加了一个跳过连接，可以使用恒等函数绕过非线性变换：
$$\begin{array}{c}{\mathbf{x}}_{\ell }=H_{\ell }({\mathbf{x}}_{\ell -1})+{\mathbf{x}}_{\ell -1}.\end{array}\text{\hspace{1em}(1)}$$

An advantage of ResNets is that the gradient can flow directly through the identity function from later layers to the earlier layers. However, the identity function and the output of Hℓ are combined by summation, which may impede the information flow in the network.
ResNets 的一个优点是梯度可以直接通过恒等函数从后面的层流到前面的层。然而，恒等函数和Hℓ的输出是通过求和结合起来的，这可能会阻碍网络中的信息流动。

Dense Connectivity

To further improve the information flow between layers we propose a different connectivity pattern: we introduce direct connections from any layer to all subsequent layers. Figure 1 illustrates the layout of the resulting DenseNet schematically. Consequently, the ℓth layer receives the feature-maps of all preceding layers, x0,…,xℓ−1, as input:
为了进一步改善层之间的信息流，我们提出了一种不同的连接模式：我们引入从任何层到所有后续层的直接连接。图 1 示意性地展示了生成的 DenseNet 的布局。因此，第 ℓ 层接收所有前面层的特征图 x0,…,xℓ−1 作为输入：
$$\begin{array}{c}{\mathbf{x}}_{\ell }=H_{\ell }([{\mathbf{x}}_0,{\mathbf{x}}_1,\dots ,{\mathbf{x}}_{l-1}]),\end{array}\text{\hspace{1em}(2)}$$

where [x0,x1,…,xℓ−1] refers to the concatenation of the feature-maps produced in layers 0,…,ℓ−1. Because of its dense connectivity we refer to this network architecture as Dense Convolutional Network (DenseNet). For ease of implementation, we concatenate the multiple inputs of Hℓ(⋅) in eq. (2) into a single tensor.
其中 [x0,x1,…,xℓ−1] 指的是第 0,…,ℓ−1 层中生成的特征图的串联。由于其密集的连接性，我们将该网络架构称为密集卷积网络（DenseNet）。为了便于实现，我们将等式中的 Hℓ(⋅) 的多个输入连接起来。 (2) 转化为单个张量。

Composite Function

Motivated by [12], we define Hℓ(⋅) as a composite function of three consecutive operations: batch normalization (BN) [14], followed by a rectified linear unit (ReLU) [6] and a 3×3 convolution (Conv).
受[12]的启发，我们将 Hℓ(⋅) 定义为三个连续操作的复合函数：批量归一化 (BN) [14]，后跟修正线性单元 (ReLU) [6] 和 3×3 卷积 (Conv)。

Pooling Layers

The concatenation operation used in Eq. (2) is not viable when the size of feature-maps changes. However, an essential part of convolutional networks is down-sampling layers that change the size of feature-maps. To facilitate down-sampling in our architecture we divide the network into multiple densely connected dense blocks; see Figure 2. We refer to layers between blocks as transition layers, which do convolution and pooling. The transition layers used in our experiments consist of a batch normalization layer and an 1×1 convolutional layer followed by a 2×2 average pooling layer.
等式中使用的串联运算。当特征图的大小发生变化时，（2）不可行。然而，卷积网络的一个重要部分是改变特征图大小的下采样层。为了便于在我们的架构中进行下采样，我们将网络划分为多个密集连接的密集块；参见图 2。我们将块之间的层称为过渡层，它执行卷积和池化。我们实验中使用的过渡层由批量归一化层和 1×1 卷积层组成，后跟 2×2 平均池化层。

Growth Rate

If each function Hℓ produces k featuremaps, it follows that the ℓth layer has k0+k×(ℓ−1) input feature-maps, where k0 is the number of channels in the input layer. An important difference between DenseNet and existing network architectures is that DenseNet can have very narrow layers, e.g., k=12. We refer to the hyperparameter k as the growth rate of the network. We show in Section 4 that a relatively small growth rate is sufficient to obtain state-of-the-art results on the datasets that we tested on. One explanation for this is that each layer has access to all the preceding feature-maps in its block and, therefore, to the network’s “collective knowledge”. One can view the feature-maps as the global state of the network. Each layer adds k feature-maps of its own to this state. The growth rate regulates how much new information each layer contributes to the global state. The global state, once written, can be accessed from everywhere within the network and, unlike in traditional network architectures, there is no need to replicate it from layer to layer.
如果每个函数 Hℓ 产生 k 个特征图，则第 ℓ 层有 k0+k×(ℓ−1) 个输入特征图，其中 k0 是输入层中的通道数。 DenseNet 和现有网络架构之间的一个重要区别是 DenseNet 可以具有非常窄的层，例如 k=12。我们将超参数 k 称为网络的增长率。我们在第 4 节中表明，相对较小的增长率足以在我们测试的数据集上获得最先进的结果。对此的一种解释是，每一层都可以访问其块中所有前面的特征图，因此可以访问网络的“集体知识”。人们可以将特征图视为网络的全局状态。每层将自己的 k 个特征图添加到该状态。增长率调节了每一层为全局状态贡献了多少新信息。全局状态一旦写入，就可以从网络中的任何位置访问，并且与传统网络架构不同，无需逐层复制它。

Table 1: Densenet architectures for ImageNet. The growth rate for the first 3 networks is k=32, and k=48 for DenseNet-161. Note that each “conv” layer shown in the table corresponds the sequence BN-ReLU-Conv. 表 1：ImageNet 的 Densenet 架构。前 3 个网络的增长率为 k=32，DenseNet-161 的增长率为 k=48。请注意，表中显示的每个“conv”层对应于序列 BN-ReLU-Conv。

Bottleneck Layers

Although each layer only produces k output feature-maps, it typically has many more inputs. It has been noted in [36], [11] that a 1×1 convolution can be introduced as bottleneck layer before each 3×3 convolution to reduce the number of input feature-maps, and thus to improve computational efficiency. We find this design especially effective for DenseNet and we refer to our network with such a bottleneck layer, i.e., to the BN-ReLU-Conv (1×1)-BN-ReLU-Conv (3×3) version of Hℓ, as DenseNet-B. In our experiments, we let each 1×1 convolution produce 4k feature-maps.
尽管每一层仅产生 k 个输出特征图，但它通常具有更多的输入。 [36]、[11]中指出，可以在每个3×3卷积之前引入1×1卷积作为瓶颈层，以减少输入特征图的数量，从而提高计算效率。我们发现这种设计对于 DenseNet 特别有效，我们将我们的网络称为具有这样的瓶颈层，即 Hℓ 的 BN-ReLU-Conv (1×1)-BN-ReLU-Conv (3×3) 版本，如下密集网络-B。在我们的实验中，我们让每个 1×1 卷积生成 4k 个特征图。

Compression

To further improve model compactness, we can reduce the number of feature-maps at transition layers. If a dense block contains m feature-maps, we let the following transition layer generate ⌊θm⌋ output feature-maps, where 0<θ≤1 is referred to as the compression factor. When θ=1, the number of feature-maps across transition layers remains unchanged. We refer the DenseNet with θ<1 as DenseNet-C, and we set θ=0.5 in our experiment. When both the bottleneck and transition layers with θ<1 are used, we refer to our model as DenseNet-BC.
为了进一步提高模型的紧凑性，我们可以减少过渡层的特征图数量。如果一个密集块包含 m 个特征图，我们让下面的过渡层生成 ⌊θm⌋ 输出特征图，其中 0<θ≤1 被称为压缩因子。当 θ=1 时，跨过渡层的特征图数量保持不变。我们将 θ<1 的 DenseNet 称为 DenseNet-C，并在实验中设置 θ=0.5。当同时使用 θ<1 的瓶颈层和过渡层时，我们将我们的模型称为 DenseNet-BC。

Implementation Details

On all datasets except ImageNet, the DenseNet used in our experiments has three dense blocks that each has an equal number of layers. Before entering the first dense block, a convolution with 16 (or twice the growth rate for DenseNet-BC) output channels is performed on the input images. For convolutional layers with kernel size 3×3, each side of the inputs is zero-padded by one pixel to keep the feature-map size fixed. We use 1×1 convolution followed by 2×2 average pooling as transition layers between two contiguous dense blocks. At the end of the last dense block, a global average pooling is performed and then a softmax classifier is attached. The feature-map sizes in the three dense blocks are 32×32, 16×16, and 8×8, respectively. We experiment with the basic DenseNet structure with configurations {L=40, k=12}, {L=100, k=12} and {L=100, k=24}. For DenseNet-BC, the networks with configurations {L=100, k=12},{L=250, k=24} and {L=190, k=40} are evaluated.
在除 ImageNet 之外的所有数据集上，我们实验中使用的 DenseNet 具有三个密集块，每个密集块具有相同数量的层。在进入第一个密集块之前，对输入图像执行 16 个（或 DenseNet-BC 增长率的两倍）输出通道的卷积。对于内核大小为 3×3 的卷积层，输入的每一侧都用一个像素进行零填充，以保持特征图大小固定。我们使用 1×1 卷积，然后使用 2×2 平均池化作为两个连续密集块之间的过渡层。在最后一个密集块的末尾，执行全局平均池化，然后附加一个 softmax 分类器。三个密集块中的特征图大小分别为 32×32、16×16 和 8×8。我们使用配置 {L=40, k=12}、{L=100, k=12} 和 {L=100, k=24} 的基本 DenseNet 结构进行实验。对于 DenseNet-BC，评估配置为 {L=100, k=12}、{L=250, k=24} 和 {L=190, k=40} 的网络。

In our experiments on ImageNet, we use a DenseNet-BC structure with 4 dense blocks on 224×224 input images. The initial convolution layer comprises 2k convolutions of size 7×7 with stride 2; the number of feature-maps in all other layers also follow from setting k. The exact network configurations we used on ImageNet are shown in Table 1.
在 ImageNet 上的实验中，我们在 224×224 输入图像上使用具有 4 个密集块的 DenseNet-BC 结构。初始卷积层包含 2k 个大小为 7×7、步幅为 2 的卷积；所有其他层中的特征图数量也取决于 k 的设置。我们在 ImageNet 上使用的确切网络配置如表 1 所示。

SECTION 4.Experiments

We empirically demonstrate DenseNet’s effectiveness on several benchmark datasets and compare with state-of-the-art architectures, especially with ResNet and its variants.
我们凭经验证明了 DenseNet 在多个基准数据集上的有效性，并与最先进的架构进行比较，特别是 ResNet 及其变体。

4.1. Datasets

CIFAR

The two CIFAR datasets [15] consist of colored natural images with 32×32 pixels. CIFAR-10 (C10) consists of images drawn from 10 and CIFAR-100 (C100) from 100 classes. The training and test sets contain 50,000 and 10,000 images respectively, and we hold out 5,000 training images as a validation set. We adopt a standard data augmentation scheme (mirroring/shifting) that is widely used for these two datasets [11], [13], [17], [22], [27], [20], [31], [33]. We denote this data augmentation scheme by a “+” mark at the end of the dataset name (e.g., C10+). For preprocessing, we normalize the data using the channel means and standard deviations. For the final run we use all 50,000 training images and report the final test error at the end of training.
两个 CIFAR 数据集 [15] 由 32×32 像素的彩色自然图像组成。 CIFAR-10 (C10) 由来自 10 个类别的图像组成，CIFAR-100 (C100) 由来自 100 个类别的图像组成。训练集和测试集分别包含 50,000 张和 10,000 张图像，我们提供 5,000 张训练图像作为验证集。我们采用广泛用于这两个数据集的标准数据增强方案（镜像/移位）[11]、[13]、[17]、[22]、[27]、[20]、[31]、[33]。我们通过数据集名称末尾的“+”标记来表示此数据增强方案（例如，C10+）。对于预处理，我们使用通道均值和标准差对数据进行标准化。对于最终运行，我们使用全部 50,000 个训练图像，并在训练结束时报告最终测试误差。

Table 2: Error rates (%) on CIFAR and SVHN datasets. k denotes network's growth rate. Results that surpass all competing methods are bold and the overall best results are blue. “+” indicates standard data augmentation (translation and/or mirroring). * indicates results run by ourselves. All the results of DenseNets without data augmentation (C10, C100, SVHN) are obtained using dropout. Densenets achieve lower error rates while using fewer parameters than ResNet. Without data augmentation, DenseNet performs better by a large margin. 表 2：CIFAR 和 SVHN 数据集的错误率 (%)。 k表示网络的增长率。超越所有竞争方法的结果是粗体的，总体最佳结果是蓝色的。 “+”表示标准数据增强（翻译和/或镜像）。 * 表示我们自己运行的结果。没有数据增强的DenseNets（C10、C100、SVHN）的所有结果都是使用dropout获得的。 Densenets 使用比 ResNet 更少的参数实现了更低的错误率。在没有数据增强的情况下，DenseNet 的性能大幅提高。

SVHN

The Street View House Numbers (SVHN) dataset [24] contains 32×32 colored digit images. There are 73,257 images in the training set, 26,032 images in the test set, and 531,131 images for additional training. Following common practice [7], [13], [20], [22], [29] we use all the training data without any data augmentation, and a validation set with 6,000 images is split from the training set. We select the model with the lowest validation error during training and report the test error. We follow [41] and divide the pixel values by 255 so they are in the [0, 1] range.
街景门牌号 (SVHN) 数据集 [24] 包含 32×32 彩色数字图像。训练集中有 73,257 张图像，测试集中有 26,032 张图像，还有 531,131 张图像用于额外训练。按照常见做法 [7]、[13]、[20]、[22]、[29]，我们使用所有训练数据而不进行任何数据增强，并从训练集中分割出包含 6,000 张图像的验证集。我们在训练期间选择验证误差最低的模型并报告测试误差。我们按照[41]将像素值除以255，这样它们就在[0, 1]范围内。

ImageNet

The ILSVRC 2012 classification dataset [2] consists 1.2 million images for training, and 50,000 for validation, from 1, 000 classes. We adopt the same data augmentation scheme for training images as in [8], [11], [12], and apply a single-crop or 10-crop with size 224×224 at test time. Following [11]–​[13], we report classification errors on the validation set.
ILSVRC 2012 分类数据集 [2] 包含来自 1, 000 个类别的 120 万张用于训练的图像和 50,000 张用于验证的图像。我们采用与[8]、[11]、[12]中相同的数据增强方案来训练图像，并在测试时应用尺寸为224×224的单裁剪或10裁剪。按照[11]-[13]，我们报告了验证集上的分类错误。

4.2. Training

All the networks are trained using stochastic gradient descent (SGD). On CIFAR and SVHN we train using batch size 64 for 300 and 40 epochs, respectively. The initial learning rate is set to 0.1, and is divided by 10 at 50% and 75% of the total number of training epochs. On ImageNet, we train models for 90 epochs with a batch size of 256. The learning rate is set to 0.1 initially, and is lowered by 10 times at epoch 30 and 60. Due to GPU memory constraints, our largest model (DenseNet-161) is trained with a mini-batch size 128. To compensate for the smaller batch size, we train this model for 100 epochs, and divide the learning rate by 10 at epoch 90.
所有网络均使用随机梯度下降（SGD）进行训练。在 CIFAR 和 SVHN 上，我们分别使用批量大小 64 进行 300 和 40 个 epoch 的训练。初始学习率设置为0.1，在训练epoch总数的50%和75%时除以10。在 ImageNet 上，我们训练模型 90 个 epoch，批量大小为 256。学习率最初设置为 0.1，并在第 30 和 60 个 epoch 降低 10 倍。由于 GPU 内存限制，我们最大的模型（DenseNet-161） ）使用小批量大小 128 进行训练。为了补偿较小的批量大小，我们将该模型训练 100 个时期，并在第 90 个时期将学习率除以 10。

Following [8], we use a weight decay of 10–4 and a Nesterov momentum [34] of 0.9 without dampening. We adopt the weight initialization introduced by [10]. For the three datasets without data augmentation, i.e., C10, C100 and SVHN, we add a dropout layer [32] after each convolutional layer (except the first one) and set the dropout rate to 0.2. The test errors were only evaluated once for each task and model setting.
按照[8]，我们使用 10-4 的权重衰减和 0.9 的 Nesterov 动量 [34]，无阻尼。我们采用[10]中引入的权重初始化。对于没有数据增强的三个数据集，即C10、C100和SVHN，我们在每个卷积层（第一个除外）之后添加一个dropout层[32]，并将dropout率设置为0.2。对于每个任务和模型设置，测试错误仅评估一次。

Table 3: The top-1 and top-5 error rates on the ImageNet validation set, with single-crop (10-crop) testing. 表 3：ImageNet 验证集上的 top-1 和 top-5 错误率，采用单次裁剪（10 次裁剪）测试。

4.3. Classification Results on CIFAR and SVHN

We train DenseNets with different depths, L, and growth rates, k. The main results on CIFAR and SVHN are shown in Table 2. To highlight general trends, we mark all results that outperform the existing state-of-the-art in boldface and the overall best result in blue.
我们训练具有不同深度 L 和增长率 k 的 DenseNet。 CIFAR 和 SVHN 的主要结果如表 2 所示。为了突出总体趋势，我们将所有优于现有最佳结果的结果用粗体标记，并将总体最佳结果标记为蓝色。

Accuracy

Possibly the most noticeable trend may originate from the bottom row of Table 2, which shows that DenseNet-BC with L=190 and k=40 outperforms the existing state-of-the-art consistently on all the CIFAR datasets. Its error rates of 3.46% on C10+ and 17.18% on C100+ are significantly lower than the error rates achieved by wide ResNet architecture [41]. Our best results on C10 and C100 (without data augmentation) are even more encouraging: both are close to 30% lower than FractalNet with drop-path regularization [17]. On SVHN, with dropout, the DenseNet with L=100 and k=24 also surpasses the current best result achieved by wide ResNet. However, the 250-layer DenseNet-BC doesn’t further improve the performance over its shorter counterpart. This may be explained by that SVHN is a relatively easy task, and extremely deep models may overfit to the training set.
最明显的趋势可能来自表 2 的底行，该表显示 L=190 和 k=40 的 DenseNet-BC 在所有 CIFAR 数据集上始终优于现有的最先进技术。其在 C10+ 上的错误率为 3.46%，在 C100+ 上的错误率为 17.18%，明显低于宽 ResNet 架构所实现的错误率 [41]。我们在 C10 和 C100（没有数据增强）上的最佳结果更加令人鼓舞：两者都比采用 drop-path 正则化的 FractalNet 低近 30% [17]。在SVHN上，在dropout的情况下，L=100、k=24的DenseNet也超过了目前宽ResNet取得的最好成绩。然而，250 层的 DenseNet-BC 并没有比其较短的对应层进一步提高性能。这可能是因为 SVHN 是一项相对容易的任务，而且极深的模型可能会过度拟合训练集。

Capacity

Without compression or bottleneck layers, there is a general trend that DenseNets perform better as L and k increase. We attribute this primarily to the corresponding growth in model capacity. This is best demonstrated by the column of C10+ and C100+. On C10+, the error drops from 5.24% to 4.10% and finally to 3.74% as the number of parameters increases from 1.0M, over 7.0M to 27.2M. On C100+, we observe a similar trend. This suggests that DenseNets can utilize the increased representational power of bigger and deeper models. It also indicates that they do not suffer from overfitting or the optimization difficulties of residual networks [11].
在没有压缩或瓶颈层的情况下，总体趋势是随着 L 和 k 的增加，DenseNet 的性能会更好。我们将这主要归因于模型容量的相应增长。 C10+ 和 C100+ 列最好地证明了这一点。在 C10+ 上，随着参数数量从 1.0M、超过 7.0M 增加到 27.2M，误差从 5.24% 下降到 4.10%，最后下降到 3.74%。在 C100+ 上，我们观察到类似的趋势。这表明 DenseNet 可以利用更大、更深的模型增强的表示能力。它还表明它们不会遭受过度拟合或残差网络的优化困难[11]。

Parameter Efficiency

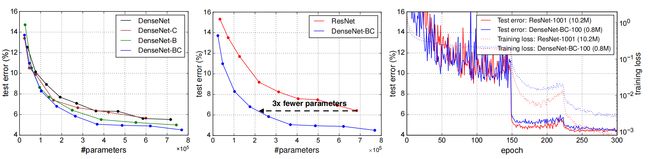
The results in Table 2 indicate that DenseNets utilize parameters more efficiently than alternative architectures (in particular, ResNets). The DenseNet-BC with bottleneck structure and dimension reduction at transition layers is particularly parameter-efficient. For example, our 250-layer model only has 15.3M parameters, but it consistently outperforms other models such as FractalNet and Wide ResNets that have more than 30M parameters. We also highlight that DenseNet-BC with L=100 and k=12 achieves comparable performance (e.g., 4.51% vs 4.62% error on C10+, 22.27% vs 22.71% error on C100+) as the 1001-layer pre-activation ResNet using 90% fewer parameters. Figure 4 (right panel) shows the training loss and test errors of these two networks on C10+. The 1001-layer deep ResNet converges to a lower training loss value but a similar test error. We analyze this effect in more detail below.
表 2 中的结果表明，DenseNet 比替代架构（特别是 ResNet）更有效地利用参数。在过渡层具有瓶颈结构和降维的 DenseNet-BC 参数效率特别高。例如，我们的 250 层模型只有 1530 万个参数，但它的性能始终优于 FractalNet 和 Wide ResNets 等具有超过 30M 参数的其他模型。我们还强调，L=100 和 k=12 的 DenseNet-BC 实现了与使用 90 的 1001 层预激活 ResNet 相当的性能（例如，C10+ 上的误差为 4.51% 与 4.62%，C100+ 上的误差为 22.27% 与 22.71%）。 % 更少的参数。图 4（右图）显示了这两个网络在 C10+ 上的训练损失和测试误差。 1001 层深度 ResNet 收敛到较低的训练损失值，但测试误差相似。我们将在下面更详细地分析这种影响。

Figure 3: Comparison of the DenseNets and ResNets top-1 error rates (single-crop testing) on the ImageNet validation dataset as a function of learned parameters (left) and FLOPs during test-time (right). 图 3：ImageNet 验证数据集上的 DenseNets 和 ResNets top-1 错误率（单次裁剪测试）的比较，作为学习参数（左）和测试期间 FLOP（右）的函数。

Overfitting

One positive side-effect of the more efficient use of parameters is a tendency of DenseNets to be less prone to overfitting. We observe that on the datasets without data augmentation, the improvements of DenseNet architectures over prior work are particularly pronounced. On C10, the improvement denotes a 29% relative reduction in error from 7.33% to 5.19%. On C100, the reduction is about 30% from 28.20% to 19.64%. In our experiments, we observed potential overfitting in a single setting: on C10, a 4× growth of parameters produced by increasing k=12 to k=24 lead to a modest increase in error from 5.77% to 5.83%. The DenseNet-BC bottleneck and compression layers appear to be an effective way to counter this trend.
更有效地使用参数的一个积极副作用是 DenseNet 不太容易过度拟合。我们观察到，在没有数据增强的数据集上，DenseNet 架构相对于之前工作的改进尤其明显。在 C10 上，改进表示误差相对减少了 29%，从 7.33% 降至 5.19%。在C100上，减少了约30%，从28.20%减少到19.64%。在我们的实验中，我们观察到单一设置中潜在的过度拟合：在 C10 上，通过将 k=12 增加到 k=24 产生的参数增长 4 倍，导致误差从 5.77% 适度增加到 5.83%。 DenseNet-BC 瓶颈和压缩层似乎是应对这一趋势的有效方法。

4.4. Classification Results on ImageNet

We evaluate DenseNet-BC with different depths and growth rates on the ImageNet classification task, and compare it with state-of-the-art ResNet architectures. To ensure a fair comparison between the two architectures, we eliminate all other factors such as differences in data preprocessing and optimization settings by adopting the publicly available Torch implementation for ResNet by [8] 1. We simply replace the ResNet model with the DenseNet-BC network, and keep all the experiment settings exactly the same as those used for ResNet. The only exception is our largest DenseNet model is trained with a mini-batch size of 128 because of GPU memory limitations; we train this model for 100 epochs with a third learning rate drop after epoch 90 to compensate for the smaller batch size.
我们在 ImageNet 分类任务上评估不同深度和增长率的 DenseNet-BC，并将其与最先进的 ResNet 架构进行比较。为了确保两种架构之间的公平比较，我们通过采用 [8] 1 中公开的 ResNet Torch 实现来消除所有其他因素，例如数据预处理和优化设置的差异。我们只需用 DenseNet-BC 替换 ResNet 模型网络，并保持所有实验设置与 ResNet 中使用的设置完全相同。唯一的例外是，由于 GPU 内存限制，我们最大的 DenseNet 模型是使用 128 的小批量进行训练的；我们训练这个模型 100 个 epoch，在 90 个 epoch 之后第三次学习率下降，以补偿较小的批量大小。

Figure 4: Left: Comparison of the parameter efficiency on C10+ between DenseNet variations. Middle: Comparison of the parameter efficiency between DenseNet-bc and (pre-activation) ResNets. Densenet-bc requires about 1/3 of the parameters as ResNet to achieve comparable accuracy. Right: Training and testing curves of the 1001-layer pre-activation ResNet [12] with more than 10M parameters and a 100-layer DenseNet with only 0.8M parameters. 图 4：左图：DenseNet 变体之间 C10+ 上的参数效率比较。中：DenseNet-bc 和（预激活）ResNet 之间的参数效率比较。 Densenet-bc 需要的参数约为 ResNet 的 1/3 就能达到相当的精度。右：具有超过 10M 参数的 1001 层预激活 ResNet [12] 和仅具有 0.8M 参数的 100 层 DenseNet 的训练和测试曲线。

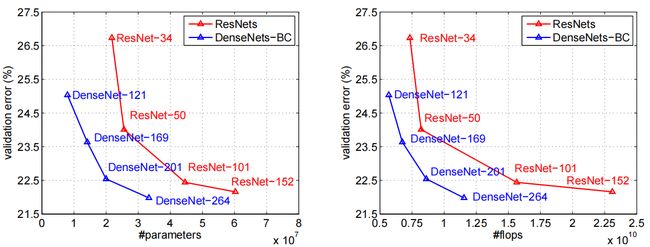
We report the single-crop and 10-crop validation errors of DenseNets on ImageNet in Table 3. Figure 3 shows the single-crop top-1 validation errors of DenseNets and ResNets as a function of the number of parameters (left) and FLOPs (right). The results presented in the figure reveal that DenseNets perform on par with the state-of-the-art ResNets, whilst requiring significantly fewer parameters and computation to achieve comparable performance. For example, a DenseNet-201 with 20M parameters model yields similar validation error as a 101-layer ResNet with more than 40M parameters. Similar trends can be observed from the right panel, which plots the validation error as a function of the number of FLOPs: a DenseNet that requires as much computation as a ResNet-50 performs on par with a ResNet-101, which requires twice as much computation.
我们在表 3 中报告了 DenseNets 在 ImageNet 上的单次裁剪和 10 次裁剪验证误差。图 3 显示了 DenseNets 和 ResNets 的单作物 top-1 验证误差与参数数量（左）和 FLOP 数（左）的函数关系。正确的）。图中显示的结果表明，DenseNet 的性能与最先进的 ResNet 相当，同时需要显着更少的参数和计算来实现可比较的性能。例如，具有 20M 参数模型的 DenseNet-201 产生的验证误差与具有超过 40M 参数的 101 层 ResNet 类似。从右侧面板中可以观察到类似的趋势，该面板将验证误差绘制为 FLOP 数量的函数：需要与 ResNet-50 一样多计算量的 DenseNet，其性能与 ResNet-101 相当，而 ResNet-101 需要两倍的计算量计算。

It is worth noting that our experimental setup implies that we use hyperparameter settings that are optimized for ResNets but not for DenseNets. It is conceivable that more extensive hyper-parameter searches may further improve the performance of DenseNet on ImageNet.2
值得注意的是，我们的实验设置意味着我们使用针对 ResNets 而不是针对 DenseNets 优化的超参数设置。可以想象，更广泛的超参数搜索可能会进一步提高DenseNet在ImageNet.2上的性能

SECTION 5.Discussion

Superficially, DenseNets are quite similar to ResNets: Eq. (2) differs from Eq. (1) only in that the inputs to Hℓ(⋅) are concatenated instead of summed. However, the implications of this seemingly small modification lead to substantially different behaviors of the two network architectures.
从表面上看，DenseNet 与 ResNet 非常相似： (2) 与等式不同。 (1) 仅在于 Hℓ(⋅) 的输入是串联而不是求和。然而，这个看似很小的修改的含义导致了两种网络架构的行为截然不同。

Model Compactness

As a direct consequence of the input concatenation, the feature-maps learned by any of the DenseNet layers can be accessed by all subsequent layers. This encourages feature reuse throughout the network, and leads to more compact models.
作为输入串联的直接结果，任何 DenseNet 层学习的特征图都可以被所有后续层访问。这鼓励了整个网络中的功能重用，并导致模型更加紧凑。

The left two plots in Figure 4 show the result of an experiment that aims to compare the parameter efficiency of all variants of DenseNets (left) and also a comparable ResNet architecture (middle). We train multiple small networks with varying depths on C10+ and plot their test accuracies as a function of network parameters. In comparison with other popular network architectures, such as AlexNet [16] or VGG-net [28], ResNets with pre-activation use fewer parameters while typically achieving better results [12]. Hence, we compare DenseNet (k=12) against this architecture. The training setting for DenseNet is kept the same as in the previous section.
图 4 中左边的两张图显示了一项实验的结果，该实验旨在比较 DenseNets 所有变体（左）和类似的 ResNet 架构（中）的参数效率。我们在 C10+ 上训练多个不同深度的小型网络，并将它们的测试精度绘制为网络参数的函数。与其他流行的网络架构（例如 AlexNet [16] 或 VGG-net [28]）相比，预激活的 ResNet 使用更少的参数，同时通常会取得更好的结果 [12]。因此，我们将 DenseNet (k=12) 与该架构进行比较。 DenseNet 的训练设置与上一节保持相同。

The graph shows that DenseNet-BC is consistently the most parameter efficient variant of DenseNet. Further, to achieve the same level of accuracy, DenseNet-BC only requires around 1/3 of the parameters of ResNets (middle plot). This result is in line with the results on ImageNet we presented in Figure 3. The right plot in Figure 4 shows that a DenseNet-BC with only 0.8M trainable parameters is able to achieve comparable accuracy as the 1001-layer (pre-activation) ResNet [12] with 10.2M parameters.
该图显示，DenseNet-BC 始终是 DenseNet 参数效率最高的变体。此外，为了达到相同水平的精度，DenseNet-BC 仅需要 ResNet 的 1/3 左右的参数（中图）。该结果与我们在图 3 中呈现的 ImageNet 上的结果一致。图 4 中的右图显示，仅具有 0.8M 可训练参数的 DenseNet-BC 能够达到与 1001 层（预激活）相当的精度ResNet [12] 具有 10.2M 参数。

Implicit Deep Supervision

One explanation for the improved accuracy of dense convolutional networks may be that individual layers receive additional supervision from the loss function through the shorter connections. One can interpret DenseNets to perform a kind of “deep supervision”. The benefits of deep supervision have previously been shown in deeply-supervised nets (DSN; [20]), which have classifiers attached to every hidden layer, enforcing the intermediate layers to learn discriminative features.
对密集卷积网络准确性提高的一种解释可能是各个层通过较短的连接从损失函数接收额外的监督。人们可以将 DenseNets 解释为执行一种“深度监督”。深度监督的好处之前已经在深度监督网络（DSN；[20]）中得到了体现，该网络将分类器附加到每个隐藏层，强制中间层学习判别性特征。

DenseNets perform a similar deep supervision in an implicit fashion: a single classifier on top of the network provides direct supervision to all layers through at most two or three transition layers. However, the loss function and gradient of DenseNets are substantially less complicated, as the same loss function is shared between all layers.
DenseNet 以隐式方式执行类似的深度监督：网络顶部的单个分类器通过最多两个或三个过渡层为所有层提供直接监督。然而，DenseNet 的损失函数和梯度要简单得多，因为所有层之间共享相同的损失函数。

Stochastic vs. Deterministic Connection

There is an interesting connection between dense convolutional networks and stochastic depth regularization of residual networks [13]. In stochastic depth, layers in residual networks are randomly dropped, which creates direct connections between the surrounding layers. As the pooling layers are never dropped, the network results in a similar connectivity pattern as DenseNet: there is a small probability for any two layers, between the same pooling layers, to be directly connected—if all intermediate layers are randomly dropped. Although the methods are ultimately quite different, the DenseNet interpretation of stochastic depth may provide insights into the success of this regularizer.
密集卷积网络和残差网络的随机深度正则化之间存在有趣的联系[13]。在随机深度中，残差网络中的层被随机丢弃，这在周围层之间创建了直接连接。由于池化层永远不会被丢弃，因此网络会产生与 DenseNet 类似的连接模式：如果所有中间层都被随机丢弃，则相同池化层之间的任何两层直接连接的概率很小。尽管这些方法最终有很大不同，但 DenseNet 对随机深度的解释可能会为该正则化器的成功提供见解。

Feature Reuse

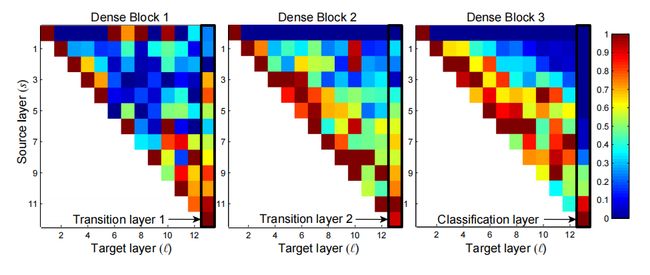
By design, DenseNets allow layers access to feature-maps from all of its preceding layers (although sometimes through transition layers). We conduct an experiment to investigate if a trained network takes advantage of this opportunity. We first train a DenseNet on C10+ with L=40 and k=12. For each convolutional layer ℓ within a block, we compute the average (absolute) weight assigned to connections with layer s. Figure 5 shows a heat-map for all three dense blocks. The average absolute weight serves as a surrogate for the dependency of a convolutional layer on its preceding layers. A red dot in position (ℓ,s) indicates that the layer ℓ makes, on average, strong use of feature-maps produced s-layers before. Several observations can be made from the plot:
根据设计，DenseNet 允许各层从其前面的所有层访问特征图（尽管有时通过过渡层）。我们进行了一项实验来调查经过训练的网络是否利用了这个机会。我们首先在 C10+ 上训练一个 DenseNet，L=40，k=12。对于块内的每个卷积层 ℓ，我们计算分配给与层 s 的连接的平均（绝对）权重。图 5 显示了所有三个密集块的热图。平均绝对权重充当卷积层对其前面层的依赖性的替代。位置 (ℓ,s) 中的红点表示层 ℓ 平均而言大量使用了之前 s 层生成的特征图。从该图中可以得出几个观察结果：

1.All layers spread their weights over many inputs within the same block. This indicates that features extracted by very early layers are, indeed, directly used by deep layers throughout the same dense block.
1.所有层将其权重分布在同一块内的多个输入上。这表明很早的层提取的特征确实被同一密集块中的深层直接使用。

2.The weights of the transition layers also spread their weight across all layers within the preceding dense block, indicating information flow from the first to the last layers of the DenseNet through few indirections.
2.过渡层的权重还将其权重分布到前面的密集块内的所有层上，表明信息通过很少的间接路径从 DenseNet 的第一层到最后一层流动。

3.The layers within the second and third dense block consistently assign the least weight to the outputs of the transition layer (the top row of the triangles), indicating that the transition layer outputs many redundant features (with low weight on average). This is in keeping with the strong results of DenseNet-BC where exactly these outputs are compressed.
3.第二和第三密集块内的层一致地将最小权重分配给过渡层的输出（三角形的顶行），表明过渡层输出许多冗余特征（平均权重较低）。这与 DenseNet-BC 的强劲结果一致，其中这些输出正是被压缩的。

4.Although the final classification layer, shown on the very right, also uses weights across the entire dense block, there seems to be a concentration towards final feature-maps, suggesting that there may be some more high-level features produced late in the network.
4.尽管最右侧显示的最终分类层也使用整个密集块的权重，但似乎集中于最终特征图，这表明网络后期可能会产生一些更高级别的特征。

SECTION 6.Conclusion

We proposed a new convolutional network architecture, which we refer to as Dense Convolutional Network (DenseNet). It introduces direct connections between any two layers with the same feature-map size. We showed that DenseNets scale naturally to hundreds of layers, while exhibiting no optimization difficulties. In our experiments, DenseNets tend to yield consistent improvement in accuracy with growing number of parameters, without any signs of performance degradation or overfitting. Under multiple settings, it achieved state-of-the-art results across several highly competitive datasets. Moreover, DenseNets require substantially fewer parameters and less computation to achieve state-of-the-art performances. Because we adopted hyperparameter settings optimized for residual networks in our study, we believe that further gains in accuracy of DenseNets may be obtained by more detailed tuning of hyperparameters and learning rate schedules.
我们提出了一种新的卷积网络架构，我们将其称为密集卷积网络（DenseNet）。它引入了具有相同特征图大小的任意两层之间的直接连接。我们证明了 DenseNet 可以自然地扩展到数百层，同时没有表现出优化困难。在我们的实验中，DenseNet 往往会随着参数数量的增加而不断提高准确性，而不会出现任何性能下降或过度拟合的迹象。在多种设置下，它在多个竞争激烈的数据集上取得了最先进的结果。此外，DenseNet 需要更少的参数和更少的计算来实现最先进的性能。由于我们在研究中采用了针对残差网络优化的超参数设置，因此我们相信，通过更详细地调整超参数和学习率，可以进一步提高 DenseNet 的准确性。

Figure 5: The average absolute filter weights of convolutional layers in a trained DenseNet. The color of pixel (s,ℓ) encodes the average L1 norm (normalized by number of input feature-maps) of the weights connecting convolutional layer s to ℓ within a dense block. Three columns highlighted by black rectangles correspond to two transition layers and the classification layer. The first row encodes weights connected to the input layer of the dense block. 图 5：经过训练的 DenseNet 中卷积层的平均绝对滤波器权重。像素 (s,ℓ) 的颜色编码密集块内连接卷积层 s 和 ℓ 的权重的平均 L1 范数（通过输入特征图的数量归一化）。由黑色矩形突出显示的三列对应于两个过渡层和分类层。第一行编码连接到密集块输入层的权重。

Whilst following a simple connectivity rule, DenseNets naturally integrate the properties of identity mappings, deep supervision, and diversified depth. They allow feature reuse throughout the networks and can consequently learn more compact and, according to our experiments, more accurate models. Because of their compact internal representations and reduced feature redundancy, DenseNets may be good feature extractors for various computer vision tasks that build on convolutional features, e.g., [4], [5]. We plan to study such feature transfer with DenseNets in future work.
在遵循简单的连接规则的同时，DenseNet 自然地融合了恒等映射、深度监督和多样化深度的特性。它们允许在整个网络中重用特征，因此可以学习更紧凑、根据我们的实验更准确的模型。由于其紧凑的内部表示和减少的特征冗余，DenseNets 可能是基于卷积特征的各种计算机视觉任务的良好特征提取器，例如[4]、[5]。我们计划在未来的工作中使用 DenseNets 研究此类特征转移。