树状数组&线段树总结
【使用总结】
经典用法:单点更新o(logn),区间查询/区间最大值(1~n,求sum),o(logn)
扩展用法:区间修改,如对[x,y]区间加上一个数k
模板题:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
class BinaryIndexTree:
def __init__(self, array: list):
'''初始化,总时间 O(n)'''
self._array = [0] + array
n = len(array)
#每遍历一个节点加到其父节点上
for i in range(1, n + 1):
j = i + (i & -i)
if j < n + 1:
self._array[j] += self._array[i]
def lowbit(self, x: int) -> int:
return x & (-x)
def update(self, idx: int, val: int):
'''将原数组idx下标更新为val, 总时间O(log n)'''
prev = self.query(idx, idx + 1) # 计算出原来的值
idx += 1
val -= prev # val 是要增加的值
while idx < len(self._array):
self._array[idx] += val
idx += self.lowbit(idx)
def query(self, begin: int, end: int) -> int:
'''返回数组[begin, end) 的和'''
return self._query(end) - self._query(begin)
def _query(self, idx: int) -> int:
'''计算数组[0, idx)的元素之和'''
res = 0
while idx > 0:
res += self._array[idx]
idx -= self.lowbit(idx)
return res【数组数组知识点】
树状数组,是一种小巧优雅的数据结构,可在 O(logn) 的时间内计算出数列的前缀和。树状数组,又称二进制索引树。
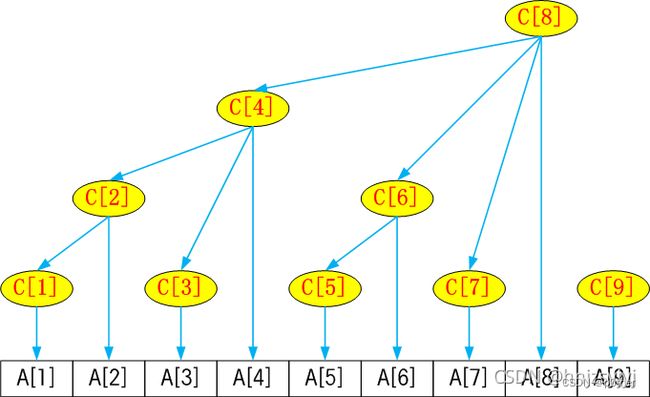
树状数组的经典实现包含两个数组:一个是存储数列元素的数组 A[],另一个是存储数列前缀和的数组 C[]。而树状数组名称的由来,恰是因为数组 C[] 呈现为树状结构。两个数组之间的关系为:C[i]=A[i-2^k+1]+A[i-2^k+2]+…+A[i],其中的 k 表示 i 的二进制表示末尾有k个连续的 0 。且由 C[] 与 A[] 的关系式易得,每个 C[i] 由数组 A[] 中的 i-(i-2^k+1)+1=2^k 个元素构成。例如,8的二进制表示为1000,其末尾有3个连续的0,则C[8]包含 2^3=8 个 A[] 数组中的元素,即C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8],这也可从树状数组的示意图中明显观察到。
在包含9个元素的树状数组中,C[i] 与 A[i] 的对应关系如下:
C[1] = A[1]
C[2] = C[1] + A[2] = A[1] + A[2]
C[3] = A[3]
C[4] = C[2] + C[3] + A[4] = A[1] + A[2] + A[3] + A[4]
C[5] = A[5]
C[6] = C[5] + A[6] = A[5] + A[6]
C[7] = A[7]
C[8] = C[4] + C[6] + C[7] + A[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
C[9] = A[9]
【树状数组的基本操作】
一、每个 C[i] 所包含的数组 A[] 中的元素个数
在编码实践中,每个 C[i] 所包含的数组 A[] 中的元素个数可有下面代码轻松得到。即:
在定义了lowbit(i)之后,C[i]=A[i-2^k+1]+A[i-2^k+2]+…+A[i],就等价于 A[i−lowbit(i)+1] ~ A[i] 的和。
int lowbit(int i){
return (-i)&i; // 返回的值等于上文中的2^k
}
二、直接前驱及直接后继
直接前驱:C[i] 的直接前驱为 C[i-lowbit(i)],即C[i]左侧紧邻的子树的根。
直接后继:C[i] 的直接后继为 C[i+lowbit(i)],即C[i]的父结点。
例如,通过树状数组的示意图,易知C[7]的直接前驱为C[6],C[6]的直接前驱为C[4],C[4]没有直接前驱;
C[5]的直接后继为C[6],C[6]的直接后继为C[8],C[8]没有直接后继。
相应的,C[i]左侧所有子树的根都是C[i]的前驱,C[i]的所有祖先都是C[i]的后继。
三、点更新
若对某个 A[i] 进行修改,如将 A[i] 加上 x,则仅需将 C[i] 及其后继(祖先)都加上 x 便可,而不必对树状数组的所有结点都进行更新。
例如,由于C[5]的后继为C[6]、C[8],所以若将 A[5] 加 2,则仅需将 C[5] 加2、C[6] 加2、C[8] 加2。这通过树状数组的示意图,更容易理解。
树状数组点更新的代码,如下所示:
void update(int i,int val) { //点更新
while(i<=n) {
c[i]+=val;
i+=lowbit(i); // i的后继(父结点)
}
}
四、查询前缀和
令 sum(i) 表示 A[] 数组中前 i 元素的前缀和,则 sum(i) 等于 C[i] 加上 C[i] 的前驱。验证如下:
∵ sum(i) = A[1] + A[2] + A[3] + ... + A[i],且有
C[1] = A[1]
C[2] = C[1] + A[2] = A[1] + A[2]
C[3] = A[3]
C[4] = C[2] + C[3] + A[4] = A[1] + A[2] + A[3] + A[4]
C[5] = A[5]
C[6] = C[5] + A[6] = A[5] + A[6]
C[7] = A[7]
C[8] = C[4] + C[6] + C[7] + A[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
C[9] = A[9]
∴ sum(1) = A[1] = C[1] → C[1] 没有前驱
sum(2) = A[1] + A[2] = C[2] → C[2] 没有前驱
sum(3) = A[1] + A[2] + A[3] = C[3] + C[2] → C[3] 的前驱是C[2]
sum(4) = A[1] + A[2] + A[3] + A[4] = C[4] → C[4] 没有前驱
sum(5) = A[1] + A[2] + A[3] + A[4] + A[5] = C[5] + C[4] → C[5] 的前驱是C[4]
sum(6) = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] = C[6] + C[4] → C[6] 的前驱是C[4]
sum(7) = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] = C[7] + C[6] + C[4] → C[7] 的前驱是C[6]、C[4]
sum(8) = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8] = C[8] + C[6] + C[4] → C[8] 没有前驱
sum(9) = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8] + A[9] = C[9] + C[8] → C[9] 的前驱是C[8]
…… …… ……
树状数组查询前缀和的代码,如下所示:
int preSum(int i) { //前缀和
int s=0;
while(i>0) { // 树状数组的下标从1开始
s+=c[i];
i-=lowbit(i); // i的前驱
}
return s;
}
五、查询区间和
若求区间 [i,j] 的和 A[i] + A[i+1] + … + A[j],利用前缀和的思想可得区间 [i,j] 的和值为 preSum(j)-preSum(i-1)。
∵ preSum(j) = A[1] + A[2] + … + A[i-1] + A[i] + … + A[j],
preSum(i-1) = A[1] + A[2] + … + A[i-1]
∴ preSum(j)-preSum(i-1) = A[i] + A[i+1] + … + A[j],得证。
树状数组查询区间和的代码,如下所示:
int segSum(int i,int j) {
return preSum(j)-preSum(i-1);
}
六、将 A[x] ~ A[y] 每个元素都加 k
树状数组的经典操作是“单点更新,区间查询”。那么在遇到“洛谷P3368”等“将区间 [x,y] 内每个数加上 k,输出第 x 个数的值”等“区间更新,单点查询”的问题时,怎么办?这就需要利用差分的思想,将“单点更新,区间查询”问题转换为熟悉的“区间更新,单点查询”问题求解。
具体方案为:设原数组为 A[i],定义差分数组 D[i]=A[i]−A[i−1],便可将对数组A[]的“区间更新”操作转化为对差分数组D[]的两次“单点更新”操作。也就是说,此时要将差分数组D[]作为新的原数组构建新的树状数组并实现相关操作。则在新的树状数组中对差分数组D[]的特定“点更新”操作将等效于对原来的原数组A[]所要求进行的“区间更新”操作。要注意,树状数组的下标从1开始,则A[0]空置未用,故有 A[0]=0。
同时,依据差分数组的定义 D[i]=A[i]−A[i−1] 可知,
D[1]=A[1]−A[0]
D[2]=A[2]−A[1]
D[3]=A[3]−A[2]
......
D[i]=A[i]−A[i-1]
上面各式子相加,可得D[1]+D[2]+D[3]+...+D[i]=A[i]-A[0],又由于A[0]=0,所以可得 A[i]=D[1]+D[2]+D[3]+...+D[i]
显然,利用上文结论 A[i]=D[1]+D[2]+D[3]+...+D[i] ,可将对数组A[]的“单点查询”操作转化为对差分数组D[]的“区间查询”操作。
下面给出一个具体实例,设数组A[]={1,7,3,6,8,5,9,2,10},依据上文所述具体方案,可得差分数组D[]={1,6,-4,3,2,-3,4,-7,8}。假如对数组A[]的区间[2,6]内的每个元素都加上2,则A[]数组变为A[]={1,9,5,8,10,7,9,2,10},差分数组则变为D[]={1,8,-4,3,2,-3,2,-7,8}。
仔细观察,发现“对数组A[]的区间[2,6]内的每个元素都加上2”这个操作执行后,对应的差分数组D[]中只有D[2]、D[7]的值发生改变。原因是,对数组A[]的区间[x,y]内的每个元素都加上k,将会使 A[x] 与前一个元素 A[x-1] 的差增加 k,A[y+1] 与 A[y] 的差减少 k,且 A[x] ~ A[y] 中其他相邻元素间的差值保持不变。所以,对数组A[]的区间[x,y]内的所有元素进行修改,只用修改D[x]与D[y+1]便可:D[x]=D[x]+k,D[y+1]=D[y+1]-k
显然,依据上述方法,便可将对数组A[]的“区间更新”操作转化为对差分数组D[]的两次“单点更新”操作。此操作需要用到树状数组“点更新”操作 update 的代码(https://blog.csdn.net/hnjzsyjyj/article/details/120559543),相关代码内容如下:
int pre=0;
int val;
for(int i=1; i<=n; i++) { //下标从1开始
scanf("%d",&val);
update(i,val-pre); //构造差分数组D[]的树状数组
pre=val;
}
update(x,k);
update(y+1,-k);
差分问题的一个题:对一个区间的修改并不一定是要全部操作一下(如对区间[l,r]中的树都加1),这样的时间复杂度很高,其实只要记录一下开头和结尾,最后从头开始按照记录进行恢复就可以了(通过先记录下来的方式减少了很多不必要的计算)。
小红组内有 n个人,大家合作完成了一个初版方案,初始时大家的愤怒值都是 0。
但是领导对方案并不满意,共需要修改 m 次方案,每次修改会先让第l到第r个人的愤怒值加 1,然后再修改方案。组内每个人都有一个愤怒阀值 a,一旦第i次修改时有人愤怒值大于愤怒阀值,他就会去找领导对线,直接将最终的方案定为第i- 1方案,并且接下来方案都不需要再修改了。
小红想知道,最终会使用第几版方案。初版方案被认为是第 0 版方案。
输入描述:
第一行输入两个整数n,m(1<=n,m <=10^5)表示数组长度和修改次数。第二行输入 n 个整数表示数组 a(0 <= ai< 10^9)。
接下来m行,每行输入两个整数l,r(1<=l<=r<=n)
输出描述:
输出一个整数表示答案。 给出这个问题的算法实现,要求时间复杂度比o(m*n)要低
def find_final_version(n, m, a, lr):
anger = [0] * (n + 1)
prefix = [0] * (n + 2)
for i in range(1, n + 1):
anger[i] = a[i - 1]
for i in range(1, m + 1):
l, r = lr[i - 1]
prefix[l] += 1
prefix[r + 1] -= 1
for i in range(1, n + 1):
prefix[i] += prefix[i - 1]
if prefix[i] > anger[i]:
return i - 1
return m【线段树知识点总结】
保存线段树数组的长度:2*n,n是原数组的大小
线段树父节点和孩子节点的关系:tree(i)=tree(2*i)+tree(2*i+1)
线段树求区间操作(i,j)的更新规则:
i的处理:若st[i]是右子结点,说明结果应包含它但不包含它的父亲,那么将结果加上st[i]并使i增加1,最后将i除以2进入下一循环; 2. 若st[i]是左子结点,它跟其右兄弟在要求的区间里,则此时直接将i除以2(即直接进入其父亲结点)进入下一循环即可;
j的处理同理:若j是左子结点,那么需要加上st[j]并使j减去1最后将j除以2进入下一循环;若j是右子结点,直接将j除以2进入下一循环即可。可以通过判断i的奇偶性来判断st[i]是左子结点还是右子结点。
简单的来说:
i的处理:i只有是右节点的时候进行计算,因为是左节点的时候其右兄弟节点也要进行计算
j的处理:j正好和i相反,当j只有是左节点的时候进行计算
class NumArray:
def __init__(self, nums: List[int]):
n = len(nums)
self.n = n
self.tree = [0]*n + nums # 线段树ST长度为2n
for i in range(n-1, 0, -1): # [1, n-1] 倒序添加,子节点之和
# ST[2i]和ST[2i+1]分别为ST[i]的左右子节点
self.tree[i] = self.tree[2*i] + self.tree[2*i+1]
def update(self, index: int, val: int) -> None:
i = index + self.n # nums下标转换到ST下标
delta = val-self.tree[i] # 变更值
while i: # 自下而上进行更新
self.tree[i] += delta
i //= 2
def sumRange(self, left: int, right: int) -> int:
i, j = left+self.n, right+self.n # nums下标转换到ST下标
summ = 0
while i<=j:
if i%2 == 1: # ST[i]是右子节点
summ += self.tree[i] # 计入ST[i],并i+1(转向下一个区间)
i += 1
if j%2 == 0: # ST[j]是左子节点
summ += self.tree[j] # 计入ST[j],并j-1(转向上一个区间)
j -= 1
i, j = i//2, j//2
return summ
【树状数组和线段树的区别】
树状数组和线段树的思想很类似,不过也有不同之处,具体区别和联系如下:
- 树状数组逻辑上是一棵普通的树,而线段树逻辑上是一颗完全二叉树;
- 两者时间复杂度级别相同, 但是树状数组的常数明显优于线段树而且代码实现简单;
- 线段树的空间复杂度在常数上为树状数组的两倍;
- 一般来讲,凡是可以使用树状数组解决的问题, 使用线段树也可以解决, 但是线段树能够解决的问题树状数组未必能够解决(例如求区间最大/小值);
【参考文献】
https://www.cnblogs.com/pigzhouyb/p/10119601.html
https://www.luogu.com.cn/problem/P2073
https://blog.csdn.net/weixin_30245867/article/details/98500495
https://www.cnblogs.com/RabbitHu/p/BIT.html