【数据结构-堆】堆
欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。
- 推荐:kuan 的首页,持续学习,不断总结,共同进步,活到老学到老
- 导航
- 檀越剑指大厂系列:全面总结 java 核心技术点,如集合,jvm,并发编程 redis,kafka,Spring,微服务,Netty 等
- 常用开发工具系列:罗列常用的开发工具,如 IDEA,Mac,Alfred,electerm,Git,typora,apifox 等
- 数据库系列:详细总结了常用数据库 mysql 技术点,以及工作中遇到的 mysql 问题等
- 懒人运维系列:总结好用的命令,解放双手不香吗?能用一个命令完成绝不用两个操作
- 数据结构与算法系列:总结数据结构和算法,不同类型针对性训练,提升编程思维,剑指大厂
非常期待和您一起在这个小小的网络世界里共同探索、学习和成长。 ✨✨ 欢迎订阅本专栏 ✨✨
博客目录
-
- 一.堆简介
-
- 1.什么是堆?
- 2.大顶堆
- 3.小顶堆
- 4.JDK 的优先队列
- 5.建堆
- 二.堆题目
-
- 1.堆排序
- 2.数组中第 K 大元素-力扣 215 题
- 3.数据流中第 K 大元素-力扣 703 题
- 4.数据流的中位数-力扣 295 题
一.堆简介
1.什么是堆?
堆(Heap)是一种重要的数据结构,通常用于实现优先队列和一些其他算法。堆具有以下主要特点:
-
完全二叉树结构: 堆通常是一个完全二叉树,这意味着树中的每个节点都有最多两个子节点,除了最后一层,其他层都是满的。这种特性使得堆可以有效地使用数组来表示,因为数组的索引操作非常高效。
-
堆序性质: 堆分为两种主要类型,最小堆和最大堆,它们都具有堆序性质。在最小堆中,每个节点的值都小于或等于其子节点的值,根节点的值最小。在最大堆中,每个节点的值都大于或等于其子节点的值,根节点的值最大。
-
堆的操作: 堆支持一些基本操作,包括插入元素、删除根节点(最小或最大元素)、查找根节点(最小或最大元素),以及堆化操作(将一个无序数组或树转化为堆)。这些操作的时间复杂度通常为 O(log n),其中 n 是堆中元素的数量。
-
应用: 堆广泛用于解决各种问题,如优先队列(用于任务调度、Dijkstra 算法等)、堆排序算法、求中位数、Top K 问题、图算法(Prim 和 Kruskal 算法中的最小生成树等)等。由于其高效的插入和删除操作,堆在这些问题中表现出色。
-
实现: 堆可以用数组来表示。在数组中,根节点通常位于索引 0,对于节点 i,其左子节点位于 2i + 1,右子节点位于 2i + 2。这种表示方法使得堆的操作更加高效。堆可以是最小堆或最大堆,具体类型取决于问题需求。
-
平衡性: 堆是一种自平衡数据结构,即在插入和删除操作后,堆仍然保持堆序性质。这是通过堆化操作来实现的,它可以向上(上滤)或向下(下滤)调整节点的位置,以满足堆的要求。
堆是一种非常有用的数据结构,用于解决许多与优先级相关的问题和算法。最小堆和最大堆的差异在于它们的堆序性质,但它们都具有相似的操作和实现方式。理解堆的基本原理和操作对于编写高效的算法非常重要。
2.大顶堆
以大顶堆为例,相对于之前的优先级队列,增加了堆化等方法
public class MaxHeap {
int[] array;
int size;
public MaxHeap(int capacity) {
this.array = new int[capacity];
}
/**
* 获取堆顶元素
*
* @return 堆顶元素
*/
public int peek() {
//获取堆顶元素
return array[0];
}
/**
* 删除堆顶元素
*
* @return 堆顶元素
*/
public int poll() {
//获取堆顶元素
int top = array[0];
//交换堆顶和堆底
swap(0, size - 1);
//容量--
size--;
//堆顶下沉
down(0);
return top;
}
/**
* 删除指定索引处元素
*
* @param index 索引
* @return 被删除元素
*/
public int poll(int index) {
int deleted = array[index];
swap(index, size - 1);
size--;
down(index);
return deleted;
}
/**
* 替换堆顶元素
* @param replaced 新元素
*/
public void replace(int replaced) {
array[0] = replaced;
down(0);
}
/**
* 堆的尾部添加元素
*
* @param offered 新元素
* @return 是否添加成功
*/
public boolean offer(int offered) {
if (size == array.length) {
return false;
}
up(offered);
size++;
return true;
}
// 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶
private void up(int offered) {
//默认插入位置在最后的index
int child = size;
while (child > 0) {
//父节点的位置
int parent = (child - 1) / 2;
//上浮
if (offered > array[parent]) {
array[child] = array[parent];
} else {
break;
}
//把父节点的坐标给child
child = parent;
}
//不要忘了赋值
array[child] = offered;
}
public MaxHeap(int[] array) {
this.array = array;
this.size = array.length;
heapify();
}
// 建堆
private void heapify() {
// 如何找到最后一个非叶子节点 size / 2 - 1,并不断往前遍历
for (int i = size / 2 - 1; i >= 0; i--) {
down(i);
}
}
// 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大
private void down(int parent) {
//找到左孩子坐标
int left = parent * 2 + 1;
//找到右孩子坐标
int right = left + 1;
int max = parent;
if (left < size && array[left] > array[max]) {
max = left;
}
if (right < size && array[right] > array[max]) {
max = right;
}
if (max != parent) { // 找到了更大的孩子
swap(max, parent);
down(max);
}
}
// 交换两个索引处的元素
private void swap(int i, int j) {
int t = array[i];
array[i] = array[j];
array[j] = t;
}
public static void main(String[] args) {
int[] array = {1, 2, 3, 4, 5, 6, 7};
MaxHeap maxHeap = new MaxHeap(array);
System.out.println(Arrays.toString(maxHeap.array));
}
}
3.小顶堆
public class MinHeap {
int[] array;
int size;
public MinHeap(int capacity) {
this.array = new int[capacity];
}
public boolean isFull() {
return size == array.length;
}
/**
* 获取堆顶元素
*
* @return 堆顶元素
*/
public int peek() {
return array[0];
}
/**
* 删除堆顶元素
*
* @return 堆顶元素
*/
public int poll() {
int top = array[0];
swap(0, size - 1);
size--;
down(0);
return top;
}
/**
* 删除指定索引处元素
*
* @param index 索引
* @return 被删除元素
*/
public int poll(int index) {
int deleted = array[index];
swap(index, size - 1);
size--;
down(index);
return deleted;
}
/**
* 替换堆顶元素
*
* @param replaced 新元素
*/
public void replace(int replaced) {
array[0] = replaced;
down(0);
}
/**
* 堆的尾部添加元素
*
* @param offered 新元素
* @return 是否添加成功
*/
public boolean offer(int offered) {
if (size == array.length) {
return false;
}
up(offered);
size++;
return true;
}
// 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶
private void up(int offered) {
int child = size;
while (child > 0) {
int parent = (child - 1) / 2;
if (offered < array[parent]) {
array[child] = array[parent];
} else {
break;
}
child = parent;
}
array[child] = offered;
}
public MinHeap(int[] array) {
this.array = array;
this.size = array.length;
heapify();
}
// 建堆
private void heapify() {
// 如何找到最后这个非叶子节点 size / 2 - 1
for (int i = size / 2 - 1; i >= 0; i--) {
down(i);
}
}
// 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大
private void down(int parent) {
int left = parent * 2 + 1;
int right = left + 1;
int min = parent;
if (left < size && array[left] < array[min]) {
min = left;
}
if (right < size && array[right] < array[min]) {
min = right;
}
if (min != parent) { // 找到了更大的孩子
swap(min, parent);
down(min);
}
}
// 交换两个索引处的元素
private void swap(int i, int j) {
int t = array[i];
array[i] = array[j];
array[j] = t;
}
}
4.JDK 的优先队列
// 大顶堆
private PriorityQueue<Integer> left = new PriorityQueue<>( (a, b) -> b-a);
// 默认是小顶堆
private PriorityQueue<Integer> right = new PriorityQueue<>();
5.建堆
- 找到最后一个非叶子节点
- 从后向前,对每个节点执行下潜
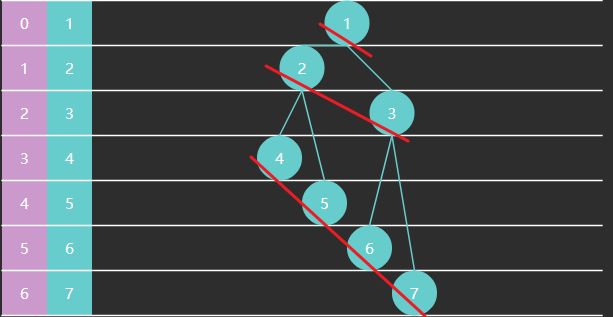
一些规律
- 一棵满二叉树节点个数为 2 h − 1 2^h-1 2h−1,如下例中高度 h = 3 h=3 h=3 节点数是 2 3 − 1 = 7 2^3-1=7 23−1=7
- 非叶子节点范围为 [ 0 , s i z e / 2 − 1 ] [0, size/2-1] [0,size/2−1]
算法时间复杂度分析
下面看交换次数的推导:设节点高度为 3
| 本层节点数 | 高度 | 下潜最多交换次数(高度-1) | |
|---|---|---|---|
| 4567 这层 | 4 | 1 | 0 |
| 23 这层 | 2 | 2 | 1 |
| 1 这层 | 1 | 3 | 2 |
每一层的交换次数为: 节点个数 ∗ 此节点交换次数 节点个数*此节点交换次数 节点个数∗此节点交换次数,总的交换次数为
$$
\begin{aligned}
& 4 * 0 + 2 * 1 + 1 * 2 \
& \frac{8}{2}*0 + \frac{8}{4}*1 + \frac{8}{8}*2 \
& \frac{8}{2^1}*0 + \frac{8}{2^2}*1 + \frac{8}{2^3}*2\
\end{aligned}
$$
即
∑ i = 1 h ( 2 h 2 i ∗ ( i − 1 ) ) \sum_{i=1}^{h}(\frac{2^h}{2^i}*(i-1)) i=1∑h(2i2h∗(i−1))
在 https://www.wolframalpha.com/ 输入
Sum[\(40)Divide[Power[2,x],Power[2,i]]*\(40)i-1\(41)\(41),{i,1,x}]
推导出
2 h − h − 1 2^h -h -1 2h−h−1
其中 2 h ≈ n 2^h \approx n 2h≈n, h ≈ log 2 n h \approx \log_2{n} h≈log2n,因此有时间复杂度 O ( n ) O(n) O(n)
二.堆题目
1.堆排序
算法描述
- heapify 建立大顶堆
- 将堆顶与堆底交换(最大元素被交换到堆底),缩小并下潜调整堆
- 重复第二步直至堆里剩一个元素
可以使用之前课堂例题的大顶堆来实现
int[] array = {1, 2, 3, 4, 5, 6, 7};
MaxHeap maxHeap = new MaxHeap(array);
System.out.println(Arrays.toString(maxHeap.array));
//判断堆的剩余元素个数
while (maxHeap.size > 1) {
//交换堆顶和堆底,把最大的移到堆底
maxHeap.swap(0, maxHeap.size - 1);
//将堆底的元素排除
maxHeap.size--;
//堆顶的元素需要下沉
maxHeap.down(0);
}
System.out.println(Arrays.toString(maxHeap.array));
2.数组中第 K 大元素-力扣 215 题
小顶堆(可删去用不到代码)
class MinHeap {
int[] array;
int size;
public MinHeap(int capacity) {
array = new int[capacity];
}
private void heapify() {
for (int i = (size >> 1) - 1; i >= 0; i--) {
down(i);
}
}
public int poll() {
swap(0, size - 1);
size--;
down(0);
return array[size];
}
public int poll(int index) {
swap(index, size - 1);
size--;
down(index);
return array[size];
}
public int peek() {
return array[0];
}
public boolean offer(int offered) {
if (size == array.length) {
return false;
}
up(offered);
size++;
return true;
}
public void replace(int replaced) {
array[0] = replaced;
down(0);
}
private void up(int offered) {
int child = size;
while (child > 0) {
int parent = (child - 1) >> 1;
if (offered < array[parent]) {
array[child] = array[parent];
} else {
break;
}
child = parent;
}
array[child] = offered;
}
private void down(int parent) {
int left = (parent << 1) + 1;
int right = left + 1;
int min = parent;
if (left < size && array[left] < array[min]) {
min = left;
}
if (right < size && array[right] < array[min]) {
min = right;
}
if (min != parent) {
swap(min, parent);
down(min);
}
}
// 交换两个索引处的元素
private void swap(int i, int j) {
int t = array[i];
array[i] = array[j];
array[j] = t;
}
}
题解 1
public int findKthLargest(int[] numbers, int k) {
MinHeap heap = new MinHeap(k);
for (int i = 0; i < k; i++) {
heap.offer(numbers[i]);
}
for (int i = k; i < numbers.length; i++) {
if(numbers[i] > heap.peek()){
heap.replace(numbers[i]);
}
}
return heap.peek();
}
求数组中的第 K 大元素,使用堆并不是最佳选择,可以采用快速选择算法
题解 2
public int findKthLargest(int[] numbers, int k) {
//小顶堆,先加入2个
PriorityQueue<Integer> queue = new PriorityQueue<>();
for (int i = 0; i < k; i++) {
queue.add(numbers[i]);
}
//再加入后面剩下的
for (int i = k; i < numbers.length; i++) {
if (numbers[i] > queue.peek()) {
queue.poll();
queue.add(numbers[i]);
}
}
return queue.peek();
}
3.数据流中第 K 大元素-力扣 703 题
上题的小顶堆加一个方法
class MinHeap {
// ...
public boolean isFull() {
return size == array.length;
}
}
题解 1
class KthLargest {
private MinHeap heap;
public KthLargest(int k, int[] nums) {
heap = new MinHeap(k);
for(int i = 0; i < nums.length; i++) {
add(nums[i]);
}
}
public int add(int val) {
if(!heap.isFull()){
heap.offer(val);
} else if(val > heap.peek()){
heap.replace(val);
}
return heap.peek();
}
}
求数据流中的第 K 大元素,使用堆最合适不过
题解 2
private PriorityQueue<Integer> queue;
private int k = 0;
public E03Leetcode703_02(int k, int[] nums) {
this.k = k;
queue = new PriorityQueue();
for (int num : nums) {
add(num);
}
}
// 此方法会被不断调用, 模拟数据流中新来的元素
public int add(int val) {
if (queue.size() < k) {
queue.offer(val);
} else if (queue.peek() < val) {
queue.poll();
queue.offer(val);
}
return queue.peek();
}
4.数据流的中位数-力扣 295 题
可以扩容的 heap, max 用于指定是大顶堆还是小顶堆
public class Heap {
int[] array;
int size;
boolean max;
public int size() {
return size;
}
public Heap(int capacity, boolean max) {
this.array = new int[capacity];
this.max = max;
}
/**
* 获取堆顶元素
*
* @return 堆顶元素
*/
public int peek() {
return array[0];
}
/**
* 删除堆顶元素
*
* @return 堆顶元素
*/
public int poll() {
int top = array[0];
swap(0, size - 1);
size--;
down(0);
return top;
}
/**
* 删除指定索引处元素
*
* @param index 索引
* @return 被删除元素
*/
public int poll(int index) {
int deleted = array[index];
swap(index, size - 1);
size--;
down(index);
return deleted;
}
/**
* 替换堆顶元素
*
* @param replaced 新元素
*/
public void replace(int replaced) {
array[0] = replaced;
down(0);
}
/**
* 堆的尾部添加元素
*
* @param offered 新元素
*/
public void offer(int offered) {
if (size == array.length) {
grow();
}
up(offered);
size++;
}
private void grow() {
int capacity = size + (size >> 1);
int[] newArray = new int[capacity];
System.arraycopy(array, 0,
newArray, 0, size);
array = newArray;
}
// 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶
private void up(int offered) {
int child = size;
while (child > 0) {
int parent = (child - 1) / 2;
boolean cmp = max ? offered > array[parent] : offered < array[parent];
if (cmp) {
array[child] = array[parent];
} else {
break;
}
child = parent;
}
array[child] = offered;
}
public Heap(int[] array, boolean max) {
this.array = array;
this.size = array.length;
this.max = max;
heapify();
}
// 建堆
private void heapify() {
// 如何找到最后这个非叶子节点 size / 2 - 1
for (int i = size / 2 - 1; i >= 0; i--) {
down(i);
}
}
// 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大
private void down(int parent) {
int left = parent * 2 + 1;
int right = left + 1;
int min = parent;
if (left < size && (max ? array[left] > array[min] : array[left] < array[min])) {
min = left;
}
if (right < size && (max ? array[right] > array[min] : array[right] < array[min])) {
min = right;
}
if (min != parent) { // 找到了更大的孩子
swap(min, parent);
down(min);
}
}
// 交换两个索引处的元素
private void swap(int i, int j) {
int t = array[i];
array[i] = array[j];
array[j] = t;
}
}
题解 1
private Heap left = new Heap(10, false);
private Heap right = new Heap(10, true);
/**
为了保证两边数据量的平衡
- 两边数据一样时,加入左边
- 两边数据不一样时,加入右边
但是, 随便一个数能直接加入吗?
- 加入左边前, 应该挑右边最小的加入
- 加入右边前, 应该挑左边最大的加入
*/
public void addNum(int num) {
if (left.size() == right.size()) {
right.offer(num);
left.offer(right.poll());
} else {
left.offer(num);
right.offer(left.poll());
}
}
/**
*
* - 两边数据一致, 左右各取堆顶元素求平均
* - 左边多一个, 取左边元素
*
*/
public double findMedian() {
if (left.size() == right.size()) {
return (left.peek() + right.peek()) / 2.0;
} else {
return left.peek();
}
}
本题还可以使用平衡二叉搜索树求解,不过代码比两个堆复杂
题解 2
/**
* 为了保证两边数据量的平衡
*
* - 两边个数一样时,左边个数加一
* - 两边个数不一样时,右边个数加一
*
* 但是, 随便一个数能直接加入吗?
*
* - 左边个数加一时, 把新元素加在右边,弹出右边最小的加入左边
* - 右边个数加一时, 把新元素加在左边,弹出左边最小的加入右边
*
*/
public void addNum(int num) {
if (left.size() == right.size()) {
right.offer(num);
left.offer(right.poll());
} else {
left.offer(num);
right.offer(left.poll());
}
}
/**
*
* - 两边数据一致, 左右各取堆顶元素求平均
* - 左边多一个, 取左边堆顶元素
*
*/
public double findMedian() {
if (left.size() == right.size()) {
return (left.peek() + right.peek()) / 2.0;
} else {
return left.peek();
}
}
// 大顶堆
private PriorityQueue<Integer> left = new PriorityQueue<>(
(a, b) -> Integer.compare(b, a)
);
// 默认是小顶堆
private PriorityQueue<Integer> right = new PriorityQueue<>();
觉得有用的话点个赞
呗。
❤️❤️❤️本人水平有限,如有纰漏,欢迎各位大佬评论批评指正!如果觉得这篇文对你有帮助的话,也请给个点赞、收藏下吧,非常感谢!
Stay Hungry Stay Foolish 道阻且长,行则将至,让我们一起加油吧!