概率栅格

欢迎访问我的博客首页。

---

1. miss 表与 hit 表

---

  miss 表和 his 表是一维数组，它们存放的都是空闲值，用于更新概率栅格。其下标 $i$ 代表旧空闲值，元素 $table[i]$ 代表旧空闲值 $i$ 的新空闲值。表的生成可以用占据几率 $odds$ 表示：

$${\mathrm{odds}}_i=\{\begin{array}{rl}\frac{p_0}{1-p_0},& i=0,\\ & \\ {\mathrm{odds}}_0\cdot \frac{1-f(i)}{f(i)},& 1\le i\le 32767.\end{array}\text{\hspace{1em}(1)}$$

其中，$p_0$ 是初始占据概率，miss 表的初始占据概率是 0.49，hit 表的初始占据概率是 0.55；函数 $f(x)$ 是从 $[1,32767]$ 到 $[0.1,0.9]$ 的线性映射，也就是下面的函数 SlowValueToBoundedFloat。再使用函数 oddsToValue 就可以求得空闲值。

# encoding=utf-8
import numpy as np
import matplotlib.pyplot as plt

kValueCount = 32768


def SlowValueToBoundedFloat(x: np.uint16, lower_bound=0.1, upper_bound=0.9) -> np.float32:
    """值转概率"""
    # x = np.clip(x, 1, 32767)
    # return (0.8 * x + 3275.8) / 32766
    x = np.clip(x, 1, 32767)
    kScale = (upper_bound - lower_bound) / (kValueCount - 2.)
    return x * kScale + (lower_bound - kScale)


def BoundedFloatToValue(x: np.float32, lower_bound=0.1, upper_bound=0.9) -> np.uint16:
    """概率转值"""
    # x = np.clip(x, 0.1, 0.9)
    # return round(40957.5 * x - 4094.75)
    x = np.clip(x, 0.1, 0.9)
    t = (x - lower_bound) * (32766. / (upper_bound - lower_bound)) + 1
    return round(t)


def oddsToValue(x):
    """占据几率转空闲值"""
    Probability = x / (1 + x)
    CorrespondenceCost = 1 - Probability
    value = BoundedFloatToValue(CorrespondenceCost) #+ 32768
    return value


def ComputeLookupTableToApplyCorrespondenceCostOdds(a):
    """生成空闲值表"""
    x = list()
    y = list()
    # odds_0
    odds0 = a / (1 - a)
    value = oddsToValue(odds0)
    x.append(0)
    y.append(value)
    # odds_i
    for i in range(1, 32768):
        oddsi = odds0 * (1 - SlowValueToBoundedFloat(i)) / SlowValueToBoundedFloat(i)
        value = oddsToValue(oddsi)
        x.append(i)
        y.append(value)
    # 空闲值表。
    return x, y


if __name__ == '__main__':
    x1, y1 = ComputeLookupTableToApplyCorrespondenceCostOdds(0.49)
    x2, y2 = ComputeLookupTableToApplyCorrespondenceCostOdds(0.55)
    x3, y3 = [0, 32767], [0, 32767]
    fig, ax = plt.subplots(figsize=(19.2, 10.8), dpi=100)
    ax.plot(x1, y1, color='red', label='miss')
    ax.plot(x2, y2, color='green', label='hit')
    ax.plot(x3, y3, color='blue', label='x=y')
    ax.set_xlim(1, 32767)
    ax.set_ylim(1, 32767)
    ax.set_xlabel('old')
    ax.set_ylabel('new')
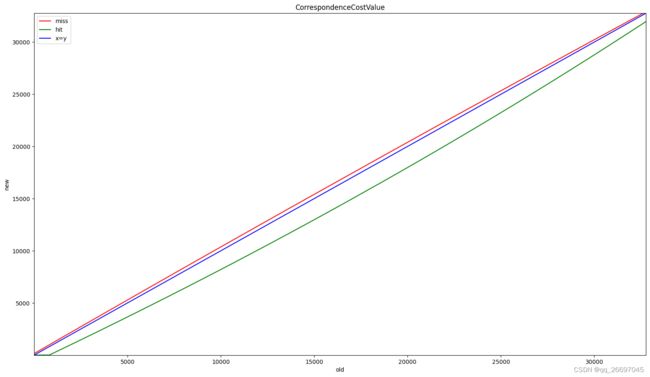
    ax.set_title('CorrespondenceCostValue')
    ax.legend(loc='best')
    fig.savefig('miss_hit.png', bbox_inches='tight')

  上面的代码生成的表的下标范围是 $[0,32767]$，元素范围是 $[1,32767]$。因此 miss 表和 hit 表的长度都是 32678。向概率栅格添加一帧距离数据时，该概率栅格会进行一轮更新。为了让每个栅格像素在此轮更新中只被更新一次，Cartographer 把表的元素都加一个更新标记 32768，如上面代码第 30 行。像素值(即空闲值)大于等于 32768 的像素即为本轮已更新的像素。更新结束后，所有被更新的像素都会减去该更新标记。

图 1 miss 表和 hit 表

  上面是我们的代码生成的 miss 表和 hit 表，不带更新标记。可以看出，miss 表的图像在直线 $x=y$ 上方，即 $x<y$，说明按照 miss 表更新空闲值变大；hit 表的图像在直线 $x=y$ 下方，即 $x>y$，说明按照 hit 表更新空闲值变小。