周报-230906

学习内容

1.将 rgbd 数据集转化为可训练的数据集

2.吴恩达深度学习（141/181）

---

学习时间

2023.08.26 — 2023.09.05

---

学习笔记

训练数据集的生成

3DMatch

这篇论文目前只进行了代码的运行，论文仅进行了初步的总结，还没有进行精读。以下是总结内容：

第1部分：

• 该部分提供了关于3DMatch的背景信息，说明了该方法的目标和应用领域，即3D数据匹配和场景重建。
• 引言介绍了传统3D匹配方法的局限性，强调了需要更有效的局部几何描述符。
• 作者提出了3DMatch，一种基于3D卷积神经网络的局部几何描述符，可用于3D数据匹配。

第2部分：

• 该部分详细介绍了3DMatch的工作原理。它包括了数据预处理、网络结构和损失函数的描述。
• 数据预处理包括将点云数据转化为TDF（Truncated Distance Function）表示，以及如何生成正负样本对。
• 网络结构描述了3DMatch的卷积神经网络架构，包括局部3D卷积层和全连接层。
• 损失函数的部分解释了如何利用孪生网络的损失函数来训练网络以学习局部几何描述符。

第3部分：

• 该部分介绍了3DMatch的训练策略，包括如何选择和生成训练数据、数据增强、损失函数的权衡和网络初始化策略。
• 训练数据的来源包括多个3D重建数据集，以及如何从中生成正负样本对。
• 数据增强包括点云的随机采样和姿态变换。
• 网络的初始化采用Xavier初始化方法。

第4部分：

• 该部分呈现了3DMatch在不同应用领域的实验结果。首先，它介绍了在Amazon Picking Challenge中的物体姿态估计实验。
• 实验结果表明，3DMatch在模型对齐任务中表现出色，特别是在姿态估计方面。
• 此外，该部分还讨论了3DMatch在3D网格上的表面对应实验，展示了其在不同物体类别之间找到几何对应关系的能力。

在生成训练数据的过程中，使用到了截断距离函数（Truncated Distance Function），TDF的主要思想是将每个空间点映射到距离最近的边界点的距离，并将这个距离进行截断。这个距离可以是正值，表示点在物体外部的距离，也可以是负值，表示点在物体内部的距离。TDF在一定截断距离之外被截断为常数。

在本篇中，有三种生成数据的方式：

• 将点云转化为 tdf
• 将网格转化为 tdf
• 将深度图转化为 tdf

而我所关注的是，是第三种方式，我对源码进行了分析与查看，并进行了运行（目前还没成功，具体问题是 cuda 版本不匹配，需要换版本，还在研究如何在一台电脑上配置多个版本的 cuda）。

TDF 体素网格的生成与以下代码相关：

// TDF voxel grid parameters
int voxel_grid_dim = 30; // In voxels
float voxel_size = 0.01f; // In meters
float trunc_margin = 5 * voxel_size;
int num_grid_pts = voxel_grid_dim * voxel_grid_dim * voxel_grid_dim;

// Compute TDF voxel grid around p1
float * voxel_grid_TDF_p1 = new float[num_grid_pts];
GetLocalPointvoxel_grid_TDF(p1_pix_x, p1_pix_y, cam_K_p1, depth_im_p1, im_height, im_width, voxel_grid_TDF_p1, voxel_grid_dim, voxel_size, trunc_margin);

// Compute TDF voxel grid around p2
ReadDepth(depth_im_file_p2, im_height, im_width, depth_im_p2);
float * voxel_grid_TDF_p2 = new float[num_grid_pts];
GetLocalPointvoxel_grid_TDF(p2_pix_x, p2_pix_y, cam_K_p2, depth_im_p2, im_height, im_width, voxel_grid_TDF_p2, voxel_grid_dim, voxel_size, trunc_margin);

// Compute TDF voxel grid around p3
ReadDepth(depth_im_file_p3, im_height, im_width, depth_im_p3);
float * voxel_grid_TDF_p3 = new float[num_grid_pts];
GetLocalPointvoxel_grid_TDF(p3_pix_x, p3_pix_y, cam_K_p3, depth_im_p3, im_height, im_width, voxel_grid_TDF_p3, voxel_grid_dim, voxel_size, trunc_margin);

现在让我们逐块解释这些相关代码块：

1. TDF体素网格参数定义：

   int voxel_grid_dim = 30; // In voxels
   float voxel_size = 0.01f; // In meters
   float trunc_margin = 5 * voxel_size;
   int num_grid_pts = voxel_grid_dim * voxel_grid_dim * voxel_grid_dim;
   

   • voxel_grid_dim：定义了TDF体素网格的维度，这里是30x30x30。
   • voxel_size：定义了每个体素的大小，这里是0.01米。
   • trunc_margin：定义了截断边界，通常是体素大小的某个倍数。
   • num_grid_pts：计算了TDF体素网格中总的体素点数，即体素网格的容量。

2. 计算TDF体素网格：

   float * voxel_grid_TDF_p1 = new float[num_grid_pts];
   GetLocalPointvoxel_grid_TDF(p1_pix_x, p1_pix_y, cam_K_p1, depth_im_p1, im_height, im_width, voxel_grid_TDF_p1, voxel_grid_dim, voxel_size, trunc_margin);
   

   这段代码用于计算TDF体素网格，特别是围绕点p1（由p1_pix_x和p1_pix_y表示）的局部TDF值。GetLocalPointvoxel_grid_TDF函数的参数包括摄像机内参、深度图像等信息，以及TDF体素网格的尺寸和截断边界。计算的结果存储在名为voxel_grid_TDF_p1的浮点数组中，该数组表示TDF体素网格的一部分。

3. 类似地，计算TDF体素网格p2和p3（应该是正样本和负样本）：

   // Compute TDF voxel grid around p2
   ReadDepth(depth_im_file_p2, im_height, im_width, depth_im_p2);
   float * voxel_grid_TDF_p2 = new float[num_grid_pts];
   GetLocalPointvoxel_grid_TDF(p2_pix_x, p2_pix_y, cam_K_p2, depth_im_p2, im_height, im_width, voxel_grid_TDF_p2, voxel_grid_dim, voxel_size, trunc_margin);
   
   // Compute TDF voxel grid around p3
   ReadDepth(depth_im_file_p3, im_height, im_width, depth_im_p3);
   float * voxel_grid_TDF_p3 = new float[num_grid_pts];
   GetLocalPointvoxel_grid_TDF(p3_pix_x, p3_pix_y, cam_K_p3, depth_im_p3, im_height, im_width, voxel_grid_TDF_p3, voxel_grid_dim, voxel_size, trunc_margin);
   

   这些代码块类似于计算局部TDF值，但这次是围绕不同的点p2和p3进行计算，并将结果分别存储在voxel_grid_TDF_p2和voxel_grid_TDF_p3中。

总结：这些代码块描述了如何基于深度信息和摄像机参数计算TDF体素网格的局部TDF值。每个TDF体素网格的局部TDF值都存储在相应的浮点数数组中，以表示TDF体素网格的一部分。这些数组可以用于后续的计算和处理，以便执行与TDF体素网格相关的任务。
其实就是以下几个步骤：

1. 获取深度图像和相机参数： 首先，从数据集中获取深度图像（或深度信息）和相机参数。深度图像是以像素为单位的深度值的二维数组，相机参数包括内参矩阵和外参矩阵，用于将像素坐标映射到相机坐标。
2. 初始化TDF体素网格： 创建一个TDF体素网格，它是一个三维数组，用于存储TDF值。网格的维度和体素大小通常需要在初始化时指定，以匹配数据集和任务的要求。
3. 遍历深度图像像素： 使用嵌套的循环遍历深度图像中的每个像素。通常，循环涵盖图像的宽度和高度。
4. 获取深度值： 在每个像素位置，从深度图像中获取深度值。深度值表示相机到场景中物体的距离。
5. 计算TDF值： 使用深度值以及相机内参和外参等信息，计算TDF值。TDF值通常表示相对于物体表面的距离，根据相机视角，越接近物体表面的点TDF值越小。
6. 存储TDF值： 将计算得到的TDF值存储在TDF体素网格的相应位置。这通常涉及到将像素坐标映射到体素网格坐标，并在网格中的相应位置存储TDF值。
7. 重复步骤3至6： 重复这些步骤，直到遍历了整个深度图像。这将为整个图像中的每个像素计算并存储TDF值。
8. 完成TDF体素网格： 一旦遍历了整个深度图像并计算了TDF值，TDF体素网格就完成了。它现在包含了整个场景的TDF信息，可供后续的任务使用。

得到的内容是一个 3 维数组，存储在 GPU 中（跟 LCD 这篇不一样，稍后会进行说明）。

LCD

已经成功运行了生成可训练数据的代码，如图：

与 3dmatch 的不同点：

• 使用的是 python 代码，而 3dmatch 是由 cuda/c++ 实现的
• 将可训练数据保存了下来，可以进行重复使用，而 3dmatch 每次训练都要重新生成

深度学习

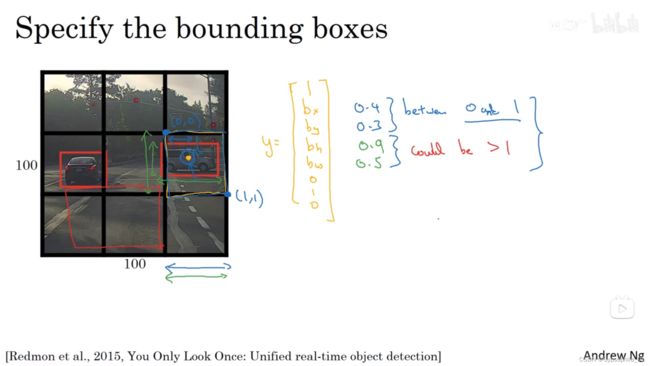
3.5 Bounding Box 预测（Bounding box predictions）

把格子均分，一起训练，得到等于格子规模的结果。因此算法效率很高。

如果中心点在这个格子里，那么其他的都不算。

中心点的 x，y 值必须小于 1，但是宽和高可以大于 1。

3.6 交并比（Intersection over union）

识别出来以后，如何看识别效果呢？

使用两个方框的交集除以并集，就是评估的指标。

这个值通常高于 0.5，如果太低就是网络不行。

3.7 非极大值抑制（Non-max suppression）

如果你的格子特别多，导致有多个格子认为中点在它们上面时，该怎么做？

我们先取出概率最高的预测，然后抛弃掉与它 IoU 值高的预测框。

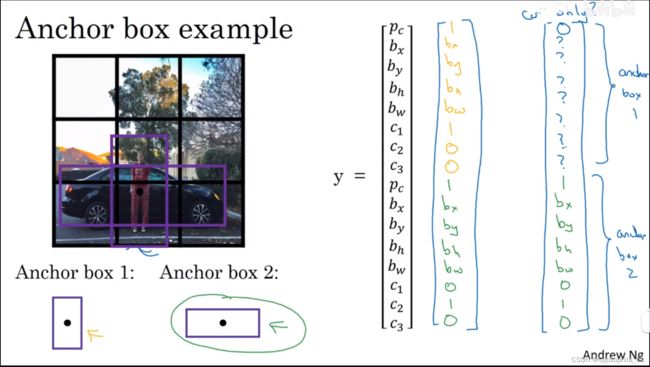
3.8 Anchor Boxes

当一个格子识别了多个框，怎么办？

把输出的向量成倍增加，我们称之为 anchor box，每一块代表不同规模的方框。

3.9 YOLO 算法（Putting it together: YOLO algorithm)

先定好 anchor box 的数量。

去除预测概率低的格子。

跑一下最大值抑制，获得最终预测。

3.10 候选区域（Region proposals(Optional)）

R-CNN 发展历程。

通过色块差异来预选一些区域，然后在这些区域中进行训练，减少滑动的次数。

算法类似基于滑动窗口的目标定位。

4.2 One-shot 学习（One-shot learning）

在识别人脸的应用中，我们网络最后的输出不可能是一个 softmax label，因为如果数据库增加的时候，就会导致重新计算网络。

现在应该使用 one-shot learning，训练一个 similarity 函数，它所做的是：输入两张图片，在经过计算后得到一个距离，这个距离在识别相同目标的时候应该比较小，不同目标的时候应该比较大。我们通过判断输出的值是否大于 $\tau$，来进行判断。

4.3 Siamese 网络（Siamese network）

我们把一张图片通过卷积网络，最终得到一个高维向量，使用这个向量作为这个图片的代表。

现在有两张图片，我们把它们都通过网络得到向量 $x^{(1)},x^{(2)}$，然后定义一个距离函数 d，得出的结果作为两个向量之间的范数$||f(x^{(1)})-f(x^{(2)})|{|}^2$。

我们把这种网络叫做 Siamese network。

4.4 Triplet 损失（Triplet loss）

A，P，N 分别表示 anchor，positive，negative。

$\alpha$ 表示 margin，目的是让 (A, P) 与 (A, N) 之间产生一定的距离。

我们使用梯度下降等算法降低 loss。
$$L(A,P,N)=max(||f(A)-f(P)|{|}^2-||f(A)-f(N)|{|}^2+\alpha ,0)$$
值得一提的是，在构建训练集的时候，我们需要好好构造三元组训练集，因为只有当这两个范数相差不大的时候，训练才有意义。关于训练集的构建的详细信息可以查阅这篇论文。

Florian Scroff, Dmitry Kalenichenko, James Philbin(2015). FaceNet: A Unified Embedding for Face Recognition and Clustering

4.5 人脸验证与二分类（Face verification and binary classification）

最后的逻辑单元该如何处理？可以使用 sigmoid function 作用于计算的结果。计算的结果比如：

k 表示向量中的某个值。
$$\hat{y}=\sigma (\sum _{k=1}^{128}{w}_i|f(x^{(i)}{)}_k-f(x^{(j)}{)}_k|+b)$$
除了这种计算方式还有很多，比如说 $\frac{(f(x^{(i)}{)}_k-f(x^{(j)}{)}_k{)}^2}{f(x^{(i)}{)}_k+f(x^{(j)}{)}_k}$ ，这个公式也被叫做 ${\chi }^2$ 公式，也被称为 $\chi$ 平方相似度。

这些公式在 DeepFace 论文中有讨论。

Taigman et al. DeepFace: Closing the gap to human-level performance in face verification

4.7 深度卷积网络学习什么？（What are deep ConvNets Learning?）

从低层到高层，识别的东西越来越复杂，在底层网络中，某个单元可能识别的是某些特定的边界。到了高层，可能会变成更加复杂的图案，甚至是人像。

更多信息可以看这篇论文：

Zeiler M D, Fergus R. Visualizing and Understanding Convolutional Networks. 2013

4.8 风格迁移的代价函数（Cost function）

定义代价函数：其中 $\alpha$ 和 $\beta$ 为两个代价函数的权重。分为了内容代价函数与风格代价函数。参考这篇论文：

Leon A. Gatys et al. A Neural Algorithm of Artistic Style
$$J(G)=\alpha \cdot J_{content}(C,G)+\beta \cdot J_{style}(S,G)$$
在内容代价中，先选择一个预训练的卷积网络，然后分别对 C 和 G 运行，我们选取某一层的激活值，计算两者差值的 L2 范数，作为内容代价函数。
$$J_{content}(C,G)=\frac{1}{2}||a^{[l](C)}-a^{[l](G)}|{|}^2$$
在风格代价中，我们按照上述步骤，取某层的激活值，分别计算两者的 Gram matrix（这样做可以获得风格，实际上所做的计算是两个单独的激活值相乘，放在对应的位置上，矩阵规模为 $n_c\cdot n_c$，原理见下图），然后计算 Frobenius 范数，作为风格代价函数。

其中 i，j，k 分别指的是 height，width，channel，矩阵 G 就是 Gram matrix。
$$\begin{gathered} G_{k{k}^{\prime }}^{[l]}=\sum _{i=1}^{n_H^{[l]}}\sum _{j=1}^{n_W^{[l]}}{a}_{i,j,k}^{[l]}\cdot a_{i,j,k^{\prime }}^{[l]} \\ {J}_{style}^{[l]}(S,G)=\frac{1}{2n_H^{[l]}{n}_W^{[l]}{n}_C^{[l]}}\sum _k\sum _{k^{\prime }}(G_{k{k}^{\prime }}^{[l](S)}-G_{k{k}^{\prime }}^{[l](G)}{)}^2 \end{gathered}$$

---