线性代数的本质(八)——内积空间
文章目录
- 内积空间
-
- 内积空间
- 正交矩阵与正交变换
- 正交投影
- 施密特正交化
- 实对称矩阵的对角化
内积空间
内积空间
三维几何空间是线性空间的一个重要例子,如果分析一下三维几何空间,我们就会发现它还具有一般线性空间不具备的重要性质:三维几何空间中向量有长度和夹角,这称为三维几何空间的度量性质。现在,我们在一般线性空间中引入度量有关的概念。
我们知道三维几何空间中向量的长度和夹角可由向量的内积来决定。内积就是一个函数,它把向量对 u , v \mathbf u,\mathbf v u,v 映射成一个数。在向量空间 V V V 中,将内积运算记为 ⟨ u , v ⟩ \lang\mathbf u,\mathbf v\rang ⟨u,v⟩,满足以下性质
- ⟨ u , v ⟩ = ⟨ v , u ⟩ \lang\mathbf u,\mathbf v\rang=\lang\mathbf v,\mathbf u\rang ⟨u,v⟩=⟨v,u⟩
- ⟨ u , v + w ⟩ = ⟨ u , v ⟩ + ⟨ u , w ⟩ \lang\mathbf u,\mathbf v+\mathbf w\rang=\lang\mathbf u,\mathbf v\rang+\lang\mathbf u,\mathbf w\rang ⟨u,v+w⟩=⟨u,v⟩+⟨u,w⟩
- c ⟨ u , v ⟩ = ⟨ c u , v ⟩ = ⟨ u , c v ⟩ c\lang\mathbf u,\mathbf v\rang=\lang c\mathbf u,\mathbf v\rang=\lang \mathbf u,c\mathbf v\rang c⟨u,v⟩=⟨cu,v⟩=⟨u,cv⟩
- ⟨ v , v ⟩ ⩾ 0 , ⟨ v , v ⟩ = 0 iff v = 0 \lang\mathbf v,\mathbf v\rang\geqslant 0,\ \lang\mathbf v,\mathbf v\rang=0\text{ iff }\mathbf v=0 ⟨v,v⟩⩾0, ⟨v,v⟩=0 iff v=0
定义了内积运算的向量空间称为内积空间(innerproductspace)。
注意,内积只给出了性质,而没给出具体的计算法则。
对于向量空间 V V V 中的任意两向量
u = u 1 e 1 + ⋯ + u n e n v = v 1 e 1 + ⋯ + v n e n \mathbf u=u_1\mathbf e_1+\cdots+u_n\mathbf e_n \\ \mathbf v=v_1\mathbf e_1+\cdots+v_n\mathbf e_n u=u1e1+⋯+unenv=v1e1+⋯+vnen
由内积的基本性质知道,其内积
⟨ u , v ⟩ = ⟨ u 1 e 1 + ⋯ + u n e n , v 1 e 1 + ⋯ + v n e n ⟩ = ∑ i , j u i v j ⟨ e i , e j ⟩ \lang\mathbf u,\mathbf v\rang =\lang u_1\mathbf e_1+\cdots+u_n\mathbf e_n,\ v_1\mathbf e_1+\cdots+v_n\mathbf e_n\rang =\sum_{i,j}u_iv_j\lang\mathbf e_i,\mathbf e_j\rang ⟨u,v⟩=⟨u1e1+⋯+unen, v1e1+⋯+vnen⟩=i,j∑uivj⟨ei,ej⟩
可见,只要知道基向量之间的内积,就可以求出任意两个向量的内积。上式用矩阵乘法表示为
⟨ u , v ⟩ = u T M v \lang\mathbf u,\mathbf v\rang=\mathbf u^TM\mathbf v ⟨u,v⟩=uTMv
其中,矩阵 M = ( δ i j ) M=(\delta_{ij}) M=(δij) 称为坐标基的度量矩阵,包含了基向量两两之间的内积
δ i j = ⟨ e i , e j ⟩ \delta_{ij}=\lang\mathbf e_i,\mathbf e_j\rang δij=⟨ei,ej⟩
定义:三维几何空间的度量概念也推广到向量空间中
- ∥ v ∥ = ⟨ v , v ⟩ \|\mathbf v\|=\sqrt{\lang\mathbf v,\mathbf v\rang} ∥v∥=⟨v,v⟩ 称为向量的长度或范数;
- dist ( u , v ) = ∥ u − v ∥ \text{dist}(\mathbf u,\mathbf v)=\|\mathbf u-\mathbf v\| dist(u,v)=∥u−v∥ 称为向量 u , v \mathbf u,\mathbf v u,v 间的距离;
- 两向量的夹角余弦 cos θ = ⟨ u , v ⟩ ∥ u ∥ ⋅ ∥ v ∥ \cos\theta=\dfrac{\lang\mathbf u,\mathbf v\rang}{\|\mathbf u\|\cdot\|\mathbf v\|} cosθ=∥u∥⋅∥v∥⟨u,v⟩
- 若 ⟨ u , v ⟩ = 0 \lang\mathbf u,\mathbf v\rang=0 ⟨u,v⟩=0 ,则称 u , v \mathbf u,\mathbf v u,v 正交(orthogonal);
- 长度为1的向量称为单位向量;
- 如果向量空间的基向量都为单位向量且两两正交,则称为标准正交基(orthonormal basis);
性质:
- ∥ v ∥ ⩾ 0 , ∥ v ∥ = 0 iff v = 0 \|\mathbf v\|\geqslant 0,\quad \|\mathbf v\|=0\text{ iff }\mathbf v=0 ∥v∥⩾0,∥v∥=0 iff v=0
- c ∥ v ∥ = ∣ c ∣ ∥ v ∥ c\|\mathbf v\|=|c|\ \|\mathbf v\| c∥v∥=∣c∣ ∥v∥
- 勾股定理:若 u , v \mathbf u,\mathbf v u,v 是 V V V 中的正交向量,则 ∥ u + v ∥ 2 = ∥ u ∥ 2 + ∥ v ∥ 2 \|\mathbf u+\mathbf v\|^2=\|\mathbf u\|^2+\|\mathbf v\|^2 ∥u+v∥2=∥u∥2+∥v∥2
- 柯西-施瓦茨不等式: ∣ ⟨ u , v ⟩ ∣ ⩽ ∥ u ∥ ⋅ ∥ v ∥ |\lang\mathbf u,\mathbf v\rang|\leqslant\|\mathbf u\|\cdot\|\mathbf v\| ∣⟨u,v⟩∣⩽∥u∥⋅∥v∥
- 三角不等式: ∥ u + v ∥ ⩽ ∥ u ∥ + ∥ v ∥ \|\mathbf u+\mathbf v\|\leqslant\|\mathbf u\|+\|\mathbf v\| ∥u+v∥⩽∥u∥+∥v∥
- 若向量组是一组两两正交的非零向量,则向量组线性无关
示例:向量空间的欧几里得内积定义为
⟨ u , v ⟩ = u T v = u 1 v 1 + u 2 v 2 + ⋯ + u n v n \lang\mathbf u,\mathbf v\rang=\mathbf u^T\mathbf v=u_1v_1+u_2v_2+\cdots+u_nv_n ⟨u,v⟩=uTv=u1v1+u2v2+⋯+unvn
即采用的是标准正交基,度量矩阵为单位阵
δ i j = { 1 , i = j 0 , i ≠ j \delta_{ij}=\begin{cases}1, &i=j \\0, &i\neq j\end{cases} δij={1,0,i=ji=j
以后,当我们讨论内积空间时,总默认采用欧几里得内积。
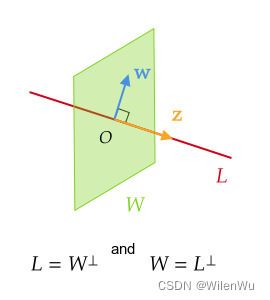
正交补:设 W W W 是 V V V 的子空间,如果向量 z \mathbf z z 与子空间 W W W 中的任意向量都正交 ,则称 z \mathbf z z 正交于 W W W。与子空间 W W W 正交的全体向量的集合称为 W W W 的正交补(orthogonal complement),并记作 W ⊥ W^{\perp} W⊥ 。
W ⊥ = { z ∈ V ∣ ∀ w ∈ W , ⟨ z , w ⟩ = 0 } W^{\perp}=\{\mathbf z\in V\mid \forall\mathbf w\in W,\lang\mathbf z,\mathbf w\rang=0\} W⊥={z∈V∣∀w∈W,⟨z,w⟩=0}
由其次方程 A x = 0 A\mathbf x=0 Ax=0 的解空间易知:
- ( row A ) ⊥ = ker A (\text{row }A)^{\perp}=\ker A (row A)⊥=kerA
- ( col A ) ⊥ = ker A T (\text{col }A)^{\perp}=\ker A^T (col A)⊥=kerAT
定理:若 z \mathbf z z 与 u 1 , u 2 , ⋯ , u p \mathbf u_1,\mathbf u_2,\cdots,\mathbf u_p u1,u2,⋯,up 均正交,则 z \mathbf z z 正交于 W = span { u 1 , u 2 , ⋯ , u p } W=\text{span }\{\mathbf u_1,\mathbf u_2,\cdots,\mathbf u_p\} W=span {u1,u2,⋯,up} 。
证:对于任意 v ∈ W \mathbf v\in W v∈W ,可线性表示为
v = x 1 u 1 + x 2 u 2 + ⋯ + x p u p \mathbf v=x_1\mathbf u_1+x_2\mathbf u_2+\cdots+x_p\mathbf u_p v=x1u1+x2u2+⋯+xpup
由内积的性质知
⟨ z , v ⟩ = x 1 ⟨ z , u 1 ⟩ + x 2 ⟨ z , u 2 ⟩ + ⋯ + x p ⟨ z , u p ⟩ = 0 \lang\mathbf z,\mathbf v\rang=x_1\lang\mathbf z,\mathbf u_1\rang+x_2\lang\mathbf z,\mathbf u_2\rang+\cdots+x_p\lang\mathbf z,\mathbf u_p\rang=0 ⟨z,v⟩=x1⟨z,u1⟩+x2⟨z,u2⟩+⋯+xp⟨z,up⟩=0
于是可知 z \mathbf z z 正交于 W W W 。
正交矩阵与正交变换
定义:若矩阵 A A A 满足 A T A = I A^TA=I ATA=I,即 A − 1 = A T A^{-1}=A^T A−1=AT,则称 A A A 为正交矩阵。
上式用 A A A 的列向量表示,即
[ a 1 T a 2 T ⋮ a n T ] ( a 1 , a 2 , ⋯ , a n ) = I n \begin{bmatrix}\mathbf a_1^T\\ \mathbf a_2^T\\ \vdots\\\mathbf a_n^T\end{bmatrix} (\mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n)=I_n a1Ta2T⋮anT (a1,a2,⋯,an)=In
于是得到
a i a j = { 1 , i = j 0 , i ≠ j \mathbf a_i\mathbf a_j=\begin{cases}1, &i=j\\ 0, &i\neq j\end{cases} aiaj={1,0,i=ji=j
定理:矩阵 A A A 为正交矩阵的充要条件是 A A A 的列向量都是单位向量且两两正交。
考虑到 A T A = I A^TA=I ATA=I 与 A A T = I AA^T=I AAT=I 等价,所以上述结论对 A A A 的行向量亦成立。
正交矩阵 A A A 对应的线性变换称为正交变换。设 u , v ∈ V \mathbf u,\mathbf v\in V u,v∈V ,则变换后的内积
⟨ A u , A v ⟩ = ( A u ) T ( A v ) = u T v = ⟨ u , v ⟩ \lang A\mathbf u,A\mathbf v\rang=(A\mathbf u)^T(A\mathbf v)=\mathbf u^T\mathbf v=\lang\mathbf u,\mathbf v\rang ⟨Au,Av⟩=(Au)T(Av)=uTv=⟨u,v⟩
定理:正交变换后向量内积保持不变,从而向量的长度、距离和夹角均保持不变。
正交投影
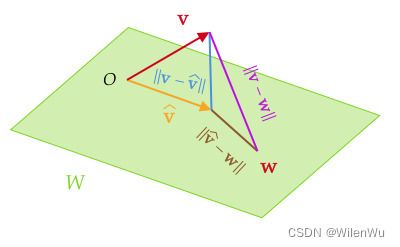
正交分解定理:设 W W W 是 V V V 的子空间,那么对于任意 v ∈ V \mathbf v\in V v∈V 可唯一表示为
v = v ^ + z \mathbf v=\hat{\mathbf v}+\mathbf z v=v^+z
其中 v ^ ∈ W , z ∈ W ⊥ \hat{\mathbf v}\in W,\mathbf z\in W^{\perp} v^∈W,z∈W⊥ 。 v ^ \hat{\mathbf v} v^ 称为 v \mathbf v v 在 W W W 上的正交投影(orthogonal projection),记作 proj W v \text{proj}_W\mathbf v projWv 。若 u 1 , u 2 , ⋯ , u p \mathbf u_1,\mathbf u_2,\cdots,\mathbf u_p u1,u2,⋯,up 是 W W W 的任意正交基,则
v ^ = proj W v = ⟨ v , u 1 ⟩ ⟨ u 1 , u 1 ⟩ u 1 + ⟨ v , u 2 ⟩ ⟨ u 2 , u 2 ⟩ u 2 + ⋯ + ⟨ v , u p ⟩ ⟨ u p , u p ⟩ u p \hat{\mathbf v}=\text{proj}_W\mathbf v=\frac{\lang\mathbf v,\mathbf u_1\rang}{\lang\mathbf u_1,\mathbf u_1\rang}\mathbf u_1+\frac{\lang\mathbf v,\mathbf u_2\rang}{\lang\mathbf u_2,\mathbf u_2\rang}\mathbf u_2+\cdots+\frac{\lang\mathbf v,\mathbf u_p\rang}{\lang\mathbf u_p,\mathbf u_p\rang}\mathbf u_p v^=projWv=⟨u1,u1⟩⟨v,u1⟩u1+⟨u2,u2⟩⟨v,u2⟩u2+⋯+⟨up,up⟩⟨v,up⟩up
证:若 u 1 , u 2 , ⋯ , u p \mathbf u_1,\mathbf u_2,\cdots,\mathbf u_p u1,u2,⋯,up 是 W W W 的任意正交基,则任意 v ∈ V \mathbf v\in V v∈V 的投影可线性表示
v ^ = x 1 u 1 + x 2 u 2 + ⋯ + x p u p \hat{\mathbf v}=x_1\mathbf u_1+x_2\mathbf u_2+\cdots+x_p\mathbf u_p v^=x1u1+x2u2+⋯+xpup
令 z = v − v ^ \mathbf z=\mathbf v-\hat{\mathbf v} z=v−v^ ,由于任意基向量 u j \mathbf u_j uj 与其他基向量正交且 z ∈ W ⊥ \mathbf z\in W^{\perp} z∈W⊥,则
⟨ z , u j ⟩ = ⟨ v − v ^ , u j ⟩ = ⟨ v , u j ⟩ − x j ⟨ u j , u j ⟩ = 0 \lang\mathbf z,\mathbf u_j\rang=\lang\mathbf v-\hat{\mathbf v},\mathbf u_j\rang= \lang\mathbf v,\mathbf u_j\rang-x_j\lang\mathbf u_j,\mathbf u_j\rang=0 ⟨z,uj⟩=⟨v−v^,uj⟩=⟨v,uj⟩−xj⟨uj,uj⟩=0
于是便求得了投影的系数
x j = ⟨ v , u j ⟩ ⟨ u j , u j ⟩ x_j=\frac{\lang\mathbf v,\mathbf u_j\rang}{\lang\mathbf u_j,\mathbf u_j\rang} xj=⟨uj,uj⟩⟨v,uj⟩
性质:设 W W W 是 V V V 的子空间, v ∈ V , v ^ = proj W v \mathbf v\in V,\hat{\mathbf v}=\text{proj}_W\mathbf v v∈V,v^=projWv
- (最佳逼近定理) v ^ \hat{\mathbf v} v^ 是 W W W 中最接近 v \mathbf v v 的点,即对于 ∀ w ∈ W , ∥ v − v ^ ∥ ⩽ ∥ v − w ∥ \forall\mathbf w\in W,\ \|\mathbf v-\hat{\mathbf v}\|\leqslant \|\mathbf v-\mathbf w\| ∀w∈W, ∥v−v^∥⩽∥v−w∥
- 若 U = ( u 1 , u 2 , ⋯ , u p ) U=(\mathbf u_1,\mathbf u_2,\cdots,\mathbf u_p) U=(u1,u2,⋯,up) 的列向量是 W W W 的单位正交基,则 proj W v = U U T v \text{proj}_W\mathbf v=UU^T\mathbf v projWv=UUTv
证:(1) 取 W W W 中的任一向量 w \mathbf w w ,由于
v − w = ( v − v ^ ) + ( v ^ − w ) \mathbf v-\mathbf w=(\mathbf v-\hat{\mathbf v})+(\hat{\mathbf v}-\mathbf w) v−w=(v−v^)+(v^−w)
由勾股定理定理知道
∥ v − w ∥ 2 = ∥ v − v ^ ∥ 2 + ∥ v ^ − w ∥ 2 \|\mathbf v-\mathbf w\|^2=\|\mathbf v-\hat{\mathbf v}\|^2+\|\hat{\mathbf v}-\mathbf w\|^2 ∥v−w∥2=∥v−v^∥2+∥v^−w∥2
由于 ∥ v ^ − w ∥ 2 ⩾ 0 \|\hat{\mathbf v}-\mathbf w\|^2\geqslant 0 ∥v^−w∥2⩾0 从而不等式得证。
(2) 由于 u 1 , u 2 , ⋯ , u p \mathbf u_1,\mathbf u_2,\cdots,\mathbf u_p u1,u2,⋯,up是 W W W 的单位正交基,那么
proj W v = ⟨ v , u 1 ⟩ u 1 + ⟨ v , u 2 ⟩ u 2 ⋯ + + ⟨ v , u p ⟩ u p = u 1 T v u 1 + u 2 T v u 2 + ⋯ + u p T v u p = U U T v \text{proj}_W\mathbf v=\lang\mathbf v,\mathbf u_1\rang\mathbf u_1+\lang\mathbf v,\mathbf u_2\rang\mathbf u_2\cdots++\lang\mathbf v,\mathbf u_p\rang\mathbf u_p\\ =\mathbf u_1^T\mathbf v\mathbf u_1+\mathbf u_2^T\mathbf v\mathbf u_2+\cdots+\mathbf u_p^T\mathbf v\mathbf u_p=UU^T\mathbf v projWv=⟨v,u1⟩u1+⟨v,u2⟩u2⋯++⟨v,up⟩up=u1Tvu1+u2Tvu2+⋯+upTvup=UUTv
施密特正交化
施密特(Schmidt)正交化方法是将向量空间 V V V 的任意一组基 a 1 , a 2 , ⋯ , a r \mathbf a_1,\mathbf a_2,\cdots,\mathbf a_r a1,a2,⋯,ar 构造成标准正交基 e 1 , e 2 , ⋯ , e r \mathbf e_1,\mathbf e_2,\cdots,\mathbf e_r e1,e2,⋯,er 的简单算法。
取
b 1 = a 1 b 2 = a 2 − b 1 T a 2 b 1 T b 1 b 1 b 3 = a 3 − b 1 T a 3 b 1 T b 1 b 1 − b 2 T a 3 b 2 T b 2 b 2 ⋯ b r = a r − b 1 T a r b 1 T b 1 b 1 − b 2 T a r b 2 T b 2 b 2 − ⋯ − b r − 1 T a r − 1 b r − 1 T b r − 1 b r − 1 \begin{aligned} &\mathbf b_1=\mathbf a_1 \\ &\mathbf b_2=\mathbf a_2-\frac{\mathbf b_1^T\mathbf a_2}{\mathbf b_1^T\mathbf b_1}\mathbf b_1 \\ &\mathbf b_3=\mathbf a_3-\frac{\mathbf b_1^T\mathbf a_3}{\mathbf b_1^T\mathbf b_1}\mathbf b_1-\frac{\mathbf b_2^T\mathbf a_3}{\mathbf b_2^T\mathbf b_2}\mathbf b_2 \\ &\cdots \\ &\mathbf b_r=\mathbf a_r-\frac{\mathbf b_1^T\mathbf a_r}{\mathbf b_1^T\mathbf b_1}\mathbf b_1-\frac{\mathbf b_2^T\mathbf a_r}{\mathbf b_2^T\mathbf b_2}\mathbf b_2-\cdots-\frac{\mathbf b_{r-1}^T\mathbf a_{r-1}}{\mathbf b_{r-1}^T\mathbf b_{r-1}}\mathbf b_{r-1} \\ \end{aligned} b1=a1b2=a2−b1Tb1b1Ta2b1b3=a3−b1Tb1b1Ta3b1−b2Tb2b2Ta3b2⋯br=ar−b1Tb1b1Tarb1−b2Tb2b2Tarb2−⋯−br−1Tbr−1br−1Tar−1br−1
那么 b 1 , b 2 , ⋯ , b r \mathbf b_1,\mathbf b_2,\cdots,\mathbf b_r b1,b2,⋯,br 是 V V V 的一组正交基
V = span { a 1 , a 2 , ⋯ , a r } = span { b 1 , b 2 , ⋯ , b r } V=\text{span }\{\mathbf a_1,\mathbf a_2,\cdots,\mathbf a_r\}=\text{span }\{\mathbf b_1,\mathbf b_2,\cdots,\mathbf b_r\} V=span {a1,a2,⋯,ar}=span {b1,b2,⋯,br}
再把它们单位化
e 1 = 1 ∥ b 1 ∥ b 1 , e 2 = 1 ∥ b 2 ∥ b 2 , ⋯ , e r = 1 ∥ b r ∥ b r \mathbf e_1=\frac{1}{\|\mathbf b_1\|}\mathbf b_1,\quad\mathbf e_2=\frac{1}{\|\mathbf b_2\|}\mathbf b_2,\quad\cdots,\quad\mathbf e_r=\frac{1}{\|\mathbf b_r\|}\mathbf b_r e1=∥b1∥1b1,e2=∥b2∥1b2,⋯,er=∥br∥1br
最终获得 V V V 的一组标准正交基。
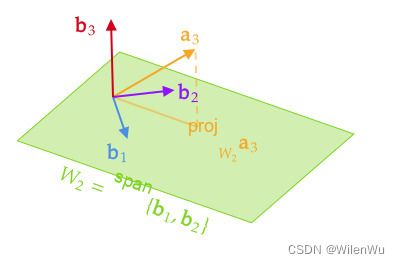
例:设 a 1 = [ 1 1 1 1 ] , a 2 = [ 0 1 1 1 ] , a 3 = [ 0 0 1 1 ] \mathbf a_1=\begin{bmatrix}1\\1\\1\\1\end{bmatrix},\mathbf a_2=\begin{bmatrix}0\\1\\1\\1\end{bmatrix},\mathbf a_3=\begin{bmatrix}0\\0\\1\\1\end{bmatrix} a1= 1111 ,a2= 0111 ,a3= 0011 是子空间 V V V的一组基,试构造 V V V 的一组正交基
解:step 1 取第一个基向量 b 1 = a 1 , W 1 = span { a 1 } = span { b 1 } \mathbf b_1=\mathbf a_1,W_1=\text{span}\{\mathbf a_1\}=\text{span}\{\mathbf b_1\} b1=a1,W1=span{a1}=span{b1}
step 2 取第二个基向量
b 2 = a 2 − proj W 1 a 2 = a 2 − b 1 T a 2 b 1 T b 1 b 1 = [ 0 1 1 1 ] − 3 4 [ 1 1 1 1 ] = [ − 3 / 4 1 / 4 1 / 4 1 / 4 ] \mathbf b_2=\mathbf a_2-\text{proj}_{W_1}\mathbf a_2= \mathbf a_2-\frac{\mathbf b_1^T\mathbf a_2}{\mathbf b_1^T\mathbf b_1}\mathbf b_1\\ =\begin{bmatrix}0\\1\\1\\1\end{bmatrix}-\frac{3}{4}\begin{bmatrix}1\\1\\1\\1\end{bmatrix}= \begin{bmatrix}-3/4\\1/4\\1/4\\1/4\end{bmatrix} b2=a2−projW1a2=a2−b1Tb1b1Ta2b1= 0111 −43 1111 = −3/41/41/41/4
为计算方便,缩放 b 2 = ( − 3 , 1 , 1 , 1 ) T \mathbf b_2=(-3,1,1,1)^T b2=(−3,1,1,1)T 。同样取 W 2 = span { b 1 , b 2 } W_2=\text{span}\{\mathbf b_1,\mathbf b_2\} W2=span{b1,b2}
step 3 取第三个基向量
b 3 = a 3 − proj W 2 a 3 = a 3 − b 1 T a 3 b 1 T b 1 b 1 − b 2 T a 3 b 2 T b 2 b 2 = [ 0 0 1 1 ] − 2 4 [ 1 1 1 1 ] − 2 12 [ − 3 1 1 1 ] = [ 0 − 2 / 3 1 / 3 1 / 3 ] \mathbf b_3=\mathbf a_3-\text{proj}_{W_2}\mathbf a_3= \mathbf a_3-\frac{\mathbf b_1^T\mathbf a_3}{\mathbf b_1^T\mathbf b_1}\mathbf b_1-\frac{\mathbf b_2^T\mathbf a_3}{\mathbf b_2^T\mathbf b_2}\mathbf b_2\\ =\begin{bmatrix}0\\0\\1\\1\end{bmatrix}- \frac{2}{4}\begin{bmatrix}1\\1\\1\\1\end{bmatrix}- \frac{2}{12}\begin{bmatrix}-3\\1\\1\\1\end{bmatrix}= \begin{bmatrix}0\\-2/3\\1/3\\1/3\end{bmatrix} b3=a3−projW2a3=a3−b1Tb1b1Ta3b1−b2Tb2b2Ta3b2= 0011 −42 1111 −122 −3111 = 0−2/31/31/3
实对称矩阵的对角化
定理:
- 实对称矩阵对应于不同特征值的特征向量必正交。
- 实对称矩阵可正交相似对角化。即对于对称矩阵 A A A ,存在正交矩阵 P P P ,使 Λ = P − 1 A P \Lambda=P^{-1}AP Λ=P−1AP 。 Λ \Lambda Λ 的对角元素为 A A A 的特征值。
证明:(1) 设实对称矩阵 A A A 对应不同特征值 λ 1 , λ 2 \lambda_1,\lambda_2 λ1,λ2 的特征向量分别为 u 1 , u 2 \mathbf u_1,\mathbf u_2 u1,u2 。则
A T = A , A u 1 = λ 1 u 1 , A u 2 = λ 2 u 2 A^T=A,\quad A\mathbf u_1=\lambda_1\mathbf u_1,\quad A\mathbf u_2=\lambda_2\mathbf u_2 AT=A,Au1=λ1u1,Au2=λ2u2
对 A u 1 = λ 1 u 1 A\mathbf u_1=\lambda_1\mathbf u_1 Au1=λ1u1两边求转置,再右乘向量 u 2 \mathbf u_2 u2,有
u 1 T A u 2 = λ 1 u 1 T u 2 \mathbf u_1^TA\mathbf u_2=\lambda_1\mathbf u_1^T\mathbf u_2 u1TAu2=λ1u1Tu2
对 A u 2 = λ 2 u 2 A\mathbf u_2=\lambda_2\mathbf u_2 Au2=λ2u2两边左乘向量 u 1 T \mathbf u_1^T u1T,有
u 1 T A u 2 = λ 2 u 1 T u 2 \mathbf u_1^TA\mathbf u_2=\lambda_2\mathbf u_1^T\mathbf u_2 u1TAu2=λ2u1Tu2
两式相减,得到
( λ 1 − λ 2 ) u 1 T u 2 = 0 (\lambda_1-\lambda_2)\mathbf u_1^T\mathbf u_2=0 (λ1−λ2)u1Tu2=0
由于 λ 1 ≠ λ 2 \lambda_1\neq \lambda_2 λ1=λ2 ,所以 u 1 T u 2 = 0 \mathbf u_1^T\mathbf u_2=0 u1Tu2=0 ,即特征向量 u 1 , u 2 \mathbf u_1,\mathbf u_2 u1,u2 正交。
例:将矩阵 A = [ 3 − 2 4 − 2 6 2 4 2 3 ] A=\begin{bmatrix}3&-2&4\\-2&6&2\\4&2&3\end{bmatrix} A= 3−24−262423 正交对角化
解:特征方程 det ( A − λ I ) = − ( λ − 7 ) 2 ( λ + 2 ) = 0 \det(A-\lambda I)=-(\lambda-7)^2(\lambda+2)=0 det(A−λI)=−(λ−7)2(λ+2)=0 ,特征值和特征向量分别为
λ = 7 : v 1 = [ 1 0 1 ] , v 2 = [ − 1 / 2 1 0 ] ; λ = − 2 : v 1 = [ − 1 − 1 / 2 1 ] \lambda=7:\mathbf v_1=\begin{bmatrix}1\\0\\1\end{bmatrix}, \mathbf v_2=\begin{bmatrix}-1/2\\1\\0\end{bmatrix}; \quad \lambda=-2:\mathbf v_1=\begin{bmatrix}-1\\-1/2\\1\end{bmatrix} λ=7:v1= 101 ,v2= −1/210 ;λ=−2:v1= −1−1/21
尽管 v 1 , v 2 \mathbf v_1,\mathbf v_2 v1,v2 是线性无关的,但它们并不正交。我们可以用施密特正交化方法,计算与 v 1 \mathbf v_1 v1 正交的 v 2 \mathbf v_2 v2 分量
z 2 = v 2 − v 1 T v 2 v 1 T v 1 v 1 = [ − 1 / 4 1 1 / 4 ] \mathbf z_2=\mathbf v_2-\frac{\mathbf v_1^T\mathbf v_2}{\mathbf v_1^T\mathbf v_1}\mathbf v_1=\begin{bmatrix}-1/4\\1\\1/4\end{bmatrix} z2=v2−v1Tv1v1Tv2v1= −1/411/4
由于 z 2 \mathbf z_2 z2 是特征值 λ = 7 \lambda=7 λ=7 的特征向量 v 1 , v 2 \mathbf v_1,\mathbf v_2 v1,v2 的线性组合,从而 z 2 \mathbf z_2 z2 是特征值 λ = 7 \lambda=7 λ=7 的特征向量。
分别将 v 1 , v 2 , v 3 \mathbf v_1,\mathbf v_2,\mathbf v_3 v1,v2,v3 标准化
u 1 = [ 1 / 2 0 1 / 2 ] , u 2 = [ − 1 / 18 4 / 18 1 / 18 ] , u 3 = [ − 2 / 3 − 1 / 3 2 / 3 ] \mathbf u_1=\begin{bmatrix}1/\sqrt{2}\\0\\1/\sqrt{2}\end{bmatrix}, \mathbf u_2=\begin{bmatrix}-1/\sqrt{18}\\4/\sqrt{18}\\1/\sqrt{18}\end{bmatrix}, \mathbf u_3=\begin{bmatrix}-2/3\\-1/3\\2/3\end{bmatrix} u1= 1/201/2 ,u2= −1/184/181/18 ,u3= −2/3−1/32/3
令
P = ( u 1 , u 2 , u 3 ) = [ 1 / 2 − 1 / 18 − 2 / 3 0 4 / 18 − 1 / 3 1 / 2 1 / 18 2 / 3 ] , Λ = [ 7 0 0 0 7 0 0 0 − 2 ] P=(\mathbf u_1,\mathbf u_2,\mathbf u_3)=\begin{bmatrix}1/\sqrt{2}&-1/\sqrt{18}&-2/3\\0&4/\sqrt{18}&-1/3\\1/\sqrt{2}&1/\sqrt{18}&2/3\end{bmatrix},\quad \Lambda=\begin{bmatrix}7&0&0\\0&7&0\\0&0&-2\end{bmatrix} P=(u1,u2,u3)= 1/201/2−1/184/181/18−2/3−1/32/3 ,Λ= 70007000−2
于是正交矩阵 P P P 将 A A A 正交对角化,即 A = P Λ P − 1 A=P\Lambda P^{-1} A=PΛP−1
对称矩阵的谱:矩阵 A A A 的特征值的集合称为 A A A 的谱(spectrum)
spec A = { λ ∈ C ∣ det ( A − λ I ) = 0 } \text{spec }A=\{\lambda\in\Complex\mid\det(A-\lambda I)=0\} spec A={λ∈C∣det(A−λI)=0}
性质 设 A A A 为 n n n 阶对称阵
- A A A 有 n n n 个实特征值(包含重复的特征值);
- 对于每一个特征值,对应的特征空间的维数等于特征方程的根的重数;
- 不同特征值的特征空间相互正交的;
- A A A 可正交対角化;
谱分解:假设对称矩阵 A = P Λ P − 1 A=P\Lambda P^{-1} A=PΛP−1 。其中 P P P 为正交矩阵,其列是 A A A 的正交特征向量 u 1 , u 2 , ⋯ , u n \mathbf u_1,\mathbf u_2,\cdots,\mathbf u_n u1,u2,⋯,un ,对应的特征值 λ 1 , λ 2 , ⋯ , λ n \lambda_1,\lambda_2,\cdots,\lambda_n λ1,λ2,⋯,λn是 Λ \Lambda Λ 的对角线元素。由于 P T = P − 1 P^T=P^{-1} PT=P−1 ,故
A = P Λ P − 1 = ( u 1 , u 2 , ⋯ , u n ) [ λ 1 λ 2 ⋱ λ n ] [ u 1 T u 2 T ⋮ u n T ] = ( λ 1 u 1 , λ 2 u 2 , ⋯ , λ n u n ) [ u 1 T u 2 T ⋮ u n T ] = λ 1 u 1 u 1 T + λ 2 u 2 u 2 T + ⋯ + λ n u n u n T \begin{aligned} A&=P\Lambda P^{-1}=(\mathbf u_1,\mathbf u_2,\cdots,\mathbf u_n) \begin{bmatrix}\lambda_1\\&\lambda_2\\&&\ddots\\&&&\lambda_n\end{bmatrix} \begin{bmatrix}\mathbf u_1^T\\\mathbf u_2^T\\\vdots\\\mathbf u_n^T\end{bmatrix} \\ &=(\lambda_1\mathbf u_1,\lambda_2\mathbf u_2,\cdots,\lambda_n\mathbf u_n) \begin{bmatrix}\mathbf u_1^T\\\mathbf u_2^T\\\vdots\\\mathbf u_n^T\end{bmatrix} \\ &=\lambda_1\mathbf u_1\mathbf u_1^T+\lambda_2\mathbf u_2\mathbf u_2^T+\cdots+\lambda_n\mathbf u_n\mathbf u_n^T \end{aligned} A=PΛP−1=(u1,u2,⋯,un) λ1λ2⋱λn u1Tu2T⋮unT =(λ1u1,λ2u2,⋯,λnun) u1Tu2T⋮unT =λ1u1u1T+λ2u2u2T+⋯+λnununT
由于它将 A A A 分解为由 A A A 的特征值确定的小块,因此这个 A A A 的表示就称为 A A A 的谱分解。 上式中的每一项都是一个秩为1的 n n n 阶方阵。例如, λ 1 u 1 u 1 T \lambda_1\mathbf u_1\mathbf u_1^T λ1u1u1T的每一列都是 u 1 \mathbf u_1 u1 的倍数。