Learning Collaborative Policies to Solve NP-hard Routing Problems 学习笔记
文章目录
- 摘要
- 一、介绍
-
-
- (0)基础
- (1)贡献
-
- 二、相关工作
-
- 0.基础
- 1.基于深度强化学习的建设型启发式
-
- (0)基础
- (1)AM-变体
- 2.基于深度强化学习的改进型启发式
- 3.带有传统求解器的混合方法
- 三、路由问题的表述
-
-
- (0)基础
- (1)状态
- (2)动作
- (3)累计奖励
- (4)构建策略
-
- 四、学习协作策略
-
- 0.基础
- 1.播种过程
-
- (0)基础
- (1)解决方案空间
- (2)策略结构
- (3)熵奖励
- (4)训练方案
- 2.修订流程
-
- (0)基础
- (1)解决方案空间
- (2)策略结构
- (3)修订奖励
- (4)训练方案
- 五、实验
-
- 0.基础
-
- (0)基础
- (1)训练超参数
- 1.目标问题和基线
-
- (0)基础
- (1)旅行商问题TSP
- (2)价值收集旅行商问题PCTSP
- (3)能力有限的车辆路由问题CVRP
- (4)具体方法
- 2.表现评估
-
- (0)基础
- (1)表现评估 N = 20, 50, 100
- (2)时间表现分析 N = 100, 500
- (3)TSPLIB的表现
- 3.消融研究
-
- (0)基础
- (1)合作政策的消融研究
- (2)附录信息
- 六、讨论
-
-
- (0)基础
- (1)未来工作
-
- 七、附录
-
- A 实验细节
-
- A.1 对目标问题的详细说明
-
- PCTSP
- CVRP
- A.2 推理阶段的详细实现
-
- SoftMax temperature
- A.3 修正器的详细实施情况
-
- TSP
- PCTSP
- CVRP
- A.4 LCP算法细节
- A.5 实验设置细节
-
- 数据集
- 运行时间对比
- 温度尺度
- B 尺度熵正则化的消融研究
- C 消融SoftMax temperature
- D 将LCP应用于其他DRL框架
- E 与修正器和改进启发式的比较
- F 不同PyTorch种子训练收敛的实验
- G 关于TSP的Real World实验的细节
- 八、主要参考文献
摘要
最近,深度强化学习(DRL)框架显示出了解决NP-hard路由问题的潜力,如没有特定问题的专家知识的旅行商问题(TSP)。尽管DRL可以用于解决复杂的问题,但DRL框架仍然难以与展示出巨大性能优势的最先进的启发式方法竞争。本文提出了一种新的层次问题解决策略,即学习协作策略(LCP),该策略可以利用播种器(seeder)和修正器(reviser)两种迭代DRL策略有效地找到接近最优的解。播种者生成尽可能多样化的候选解决方案(种子),同时致力于探索完整的组合动作空间(即分配动作的序列)。播种器生成尽可能多样化的候选解决方案(seeds),同时致力于探索完整的组合动作空间(即分配动作的序列)。为此,本文使用一个简单而有效的熵正则化奖励来训练播种者的策略,以鼓励播种器找到不同的解决方案。另一方面,修正器修改由播种器生成的每个候选解决方案;它将整个轨迹划分为子行程,并同时修改每个子行程,以最小化其旅行距离。因此,训练修正器以提高候选解决方案的质量,重点关注减少的解决方案空间(这有利于开发)。大量的实验表明,所提出的双策略协作方案改进了单策略DRL框架,包括TSP、奖收集TSP(PCTSP)和有容量的车辆路由问题(CVRP)。
一、介绍
(0)基础
路由是一个组合优化问题,是离散数学和计算理论的突出领域之一。在路由问题中,旅行商问题(TSP)是一个典型的例子。TSP可以应用于各种工程领域的现实问题,如机器人路由、生物学和电气设计自动化(EDA),通过将约束和目标扩展到现实世界的设置:创造的TSP变体是TSP的扩展版本。然而,TSP及其变体是NP-hard的,这使得设计一个精确的求解器具有挑战性。
由于NP-hard,类似TSP的问题的求解器依赖于混合整数线性规划(MILP)求解器和手工制作的启发式。虽然它们通常在目标问题上提供显著的性能,但传统的方法有一些局限性。首先,在MILP求解器的情况下,目标函数和约束必须表述成线性形式,但许多现实世界的路由应用,包括生物学和EDA,都有一个非线性的目标。其次,手工制作的启发式方法依赖于对目标问题的专家知识,因此很难解决其他问题。也就是说,每当目标问题改变时,算法也必须重新设计。
针对传统方法的局限性,提出了深度强化学习(DRL)路由框架。DRL的一个好处是,DRL的奖励可以是任何值,甚至来自黑盒模拟器;因此,DRL可以克服MILP在实际应用中的局限性。此外,DRL框架可以自动设计较少依赖手工方式的求解器。
值得注意的是,本文研究的主要目标并不是优于特定问题解决器,如Concorde——一个TSP问题求解器。然而,本文基于DRL的问题解决策略最终侧重于实际应用,包括智能运输、生物序列设计、电气设备上的路由和设备放置。因此,本文评估了DRL框架在类似TSP问题上的性能,作为实际应用的潜在适用性基准,包括速度、最优性、可伸缩性和对其他问题的扩展能力。类似TSP的问题是很好的基准,因为它们有各种基线可以进行比较,并且可以很容易地建模和评估。
(1)贡献
本文提出了一种新的DRL方案,提出了学习协作策略(LCP),一种具有播种器和修正器两种策略的分层求解协议。播种器生成各种候选解决方案(种子),每个解决方案将由修正器迭代修改,以生成微调的解决方案。
拥有多样化的候选解决方案是很重要的,因为它提供了一个更好的机会,在其中找到最好的解决方案。因此,播种者致力于探索完整的组合动作空间(即分配动作的序列),从而提供尽可能多样化的候选解决方案。探索整个组合动作空间是很重要的,因为解决方案的质量随着其组成的不同而高度波动;然而,探索组合动作空间本质上是困难的,因为它不可避免地有许多可能的解决方案。因此,本研究提出了一种应用熵最大化方案的有效探索策略。
修正器修改由播种器生成的每个候选解决方案。修正器致力于利用策略(即关于问题的派生知识)来提高候选解决方案的质量。修正器将整个轨迹划分为子行程,并对每个子行程进行修正,以平行的方式尽量减少其旅行距离。这个方案提供了两个优点: (a)搜索限制解决方案空间可以更高效,因为与完整轨迹当使用强化学习得出政策相比,奖励信号对应的子路径的变量更少,和(b)搜索的种子可以并行加快修改过程。
本文的方法最显著的优势是,修正器可以重新评估从播种器中获得的、多元化但被低估的候选方案,而不会过早地放弃它。由于播种器探索了整个轨迹,因此在局部子轨迹中可能存在错误。因此,必须在本地纠正这些错误,以提高解决方案的质量。所提出的修改方案通过对全解进行分解和局部更新,使修改过程并行化。因此,它允许修正器在比传统局部搜索相比的单一推理中搜索更大的解决方案空间(即修正器的迭代次数小于传统的局部搜索2-opt ,或基于DRL的2-opt ),从而降低了计算成本。因此,可以保留候选方案,而不因为计算成本而提前排除它们。
该方法是一种与神经结构无关的方法,可应用于各种神经结构。播种器和修正器可以用任何神经结构参数化;本研究利用组合优化的代表性DRL模型AM对播种器和修正器进行参数化。实验结果表明,LCP改进了目标神经结构AM,在TSP、PCTSP和CVRP( N = 20 、 50 、 100 、 500 N = 20、50、100、500 N=20、50、100、500, N N N:节点数)和实际问题上优于竞争的DRL框架。此外,通过进行广泛的消融研究,我们展示了所提出的技术,包括熵正则化方案和修正方案,明显有助于性能的提高。
二、相关工作
0.基础
DRL框架在解决各种路由问题方面不断取得进展。DRL框架可以生成不依赖于目标问题的基本事实标签的求解器:它可以应用于未探索的问题。基于DRL的方法可以分为两部分:建设性启发式和改进启发式。作者调查了这两个类别以及当前新兴的机器学习(ML)与传统求解器的混合方法。
1.基于深度强化学习的建设型启发式
(0)基础
Bello等人引入了一种由指针网络组成的策略参数化的 actor-critic算法。他们提出了一个建设性的马尔可夫决策过程(MDP),其中的动作被定义为选择一个未服务的节点来访问,给出一个部分的解决方案;该策略被训练为添加一个节点,以按顺序提供一个完整的解决方案。后来,基于DRL的构造启发式来设计神经网络的体系结构被开发,同时保留构造的MDP。Khalil等人提出了一个具有图嵌入结构的DRL框架。Nazari等人,Duedon等人和Kool等人使用transformer重新设计了指针网络,并使用策略梯度方法对其进行训练。Kool等人的AM报告了各种NP-hard路由问题的大量结果,包括高速计算中的TSP、PCTSP、CVRP和定向问题(OP)。
(1)AM-变体
在AM取得有意义的成功后,许多研究从AM扩展出来。许多工程领域和行业都将AM应用到他们的领域中。例如,Liao等人提出了一种基于AM的电路路由算法。
一些研究集中在通过简单的技术来提高AM对TSP等经典路由问题的性能。Kwon等人提出了高效的的AM POMO强化学习方法。他们提出了一种新的RL基线,可以利用TSP和CVRP的特定问题的特性来减少AM的训练方差。此外,他们还提出了一种有效的TSP和CVRP后处理算法。然而,他们提出的方法有一个局限性,因为它是针对问题的,因为它使用了TSP和CVRP的域特性(例如,他们的方法仅限于应用于PCTSP.)。
Xin等人提出了AM型DRL模型——MDAM,用于NP-hard路由问题。他们的方法学习多个调幅解码器,并通过多个解码器推导出各种解决方案。增加解决方案多样性的目标与我们的研究类似。然而,本文的研究是不同的,本文增加了单个解码器的熵,并通过一个修正器改进了各种解决方案的错误。
2.基于深度强化学习的改进型启发式
与构造MDP不同,基于DRL的改进启发式被设计用来迭代改进完成的解决方案。大多数关于基于DRL的改进启发式的研究都是受到经典的局部搜索算法的启发,如2-opt 和大邻域搜索(LNS)。
Chen等人提出了一个基于DRL的本地搜索框架,称为NeuRewriter,该框架在CVRP和作业调度问题上显示出很好的性能。Wu等人和Costa等人通过学习2个选项,提出了一个基于DRL的TSP求解器。他们的方法改进了随机生成的解,与Chen等人的方法不同,重写了由传统的启发式求解器给出的解。Hottung & Tierney 提出了一种新的VRP搜索方法,它破坏和修复一个重复启发LNS的解决方案。他们的方法在CVRP上具有良好的性能。
改进启发式方法通常比建设性启发式方法表现出更好的性能,但通常比建设性启发式方法表现得更慢。在TSP的情况下,神经网络的建设性启发式推断的数量与要访问的城市的数量相同。然而,改进启发式的推断的数量通常要大得多。
3.带有传统求解器的混合方法
最近有一些关于使用传统求解器的混合方法有很好的研究。Lu等人提出了一种混合方法,其中学习策略来控制改进操作符(手工启发式)。值得注意的是,它们的性能优于LKH3,LKH3在机器学习(ML)社区中被广泛认为是值得挑战的方法。Joshi等人,将图神经网络(GNN)模型与波束搜索算法相结合。他们用监督学习训练GNN,以生成候选节点的命中图。然后经过训练的GNN减少了一个改进启发式的搜索空间。类似地,Fu等将监督GNN模型与蒙特卡罗树搜索(MCTS)结合,Kool等将监督GNN模型与动态规划结合。他们的方法取得了显著的性能,表明ML方法可以有效地与传统运筹学(OR)方法协作。
混合方法和基于DRL的方法的研究范围是不同的。混合方法可以通过与经典求解器的协作来克服目标任务中的经典求解器。然而,混合方法继承了经典求解器的局限性,即对其他任务的可扩展性较差。基于DRL的方法可以应用于各种现实世界的任务,而没有一个经典的求解器;我们也可以利用基于DRL的任务来完成未被探索的任务。本文研究了基于DRL的无经典求解器的np硬路由方法。
三、路由问题的表述
(0)基础
本节以给定二维欧几里得TSP的马尔可夫决策过程(MDP)公式。针对其他问题的MDP的公式见附录A.1。
TSP的主要目标是发现最短的哈密顿回路(Hamiltonian cycle)。TSP图课题被表示为N个节点序列的2D欧几里得空间, s = { x i } i = 1 N \boldsymbol{s}=\left\{x_i\right\}_{i=1}^N s={xi}i=1N其中 x i ∈ R 2 x_i \in \mathbb{R}^2 xi∈R2。接着,TSP解决方案可以被表示为输入序列的 π \pi π排列:
π = ⋃ t = 1 t = N { π t } , π t ∈ { 1 , … , N } , π t 1 ≠ π t 2 if t 1 ≠ t 2 \pi=\bigcup_{t=1}^{t=N}\left\{\pi_t\right\}, \quad \pi_t \in\{1, \ldots, N\}, \quad \pi_{t_1} \neq \pi_{t_2} \quad \text { if } \quad t_1 \neq t_2 π=t=1⋃t=N{πt},πt∈{1,…,N},πt1=πt2 if t1=t2
目标是最小化路程长度 L ( π ∣ s ) = ∑ t = 1 N − 1 ∥ x π t + 1 − x π t ∥ 2 + ∥ x π N − x π 1 ∥ 2 L(\boldsymbol{\pi} \mid \boldsymbol{s})=\sum_{t=1}^{N-1}\left\|x_{\pi_{t+1}}-x_{\pi_t}\right\|_2+\left\|x_{\pi_N}-x_{\pi_1}\right\|_2 L(π∣s)=∑t=1N−1∥xπt+1−xπt∥2+∥xπN−xπ1∥2 。
接着,作者制定了TSP的建设性马尔可夫决策过程(MDP)。
(1)状态
MDP的状态表示为TSP的部分解或一系列先前选择的动作: π 1 : t − 1 \pi_{1: t-1} π1:t−1
(2)动作
操作被定义为选择一个未提供服务的任务。因此任务可以被标识为 π t \pi_t πt其中 π t ∈ { { 1 , … , N } \ { π 1 : t − 1 } } \pi_t \in\left\{\{1, \ldots, N\} \backslash\left\{\boldsymbol{\pi}_{1: t-1}\right\}\right\} πt∈{{1,…,N}\{π1:t−1}}
(3)累计奖励
本文将问题实例中解决方案的累积奖励(一个分配序列)定义为比赛时间的负值: − L ( π ∣ s ) -L(\pi \mid s) −L(π∣s)
(4)构建策略
最后坐着定义构建策略 p ( π ∣ s ) p(\pi|s) p(π∣s),这可以从TSP图 s s s中生成解决方案 π \pi π。构建策略 p ( π ∣ s ) p(\pi|s) p(π∣s)可以被分解为:
p ( π ∣ s ) = ∏ t = 1 t = N p θ ( π t ∣ π 1 : t − 1 , s ) p(\boldsymbol{\pi} \mid \boldsymbol{s})=\prod_{t=1}^{t=N} p_\theta\left(\pi_t \mid \boldsymbol{\pi}_{1: t-1}, \boldsymbol{s}\right) p(π∣s)=t=1∏t=Npθ(πt∣π1:t−1,s)
其中 p θ ( π t ∣ π 1 : t − 1 , s ) p_\theta\left(\pi_t \mid \boldsymbol{\pi}_{1: t-1}, \boldsymbol{s}\right) pθ(πt∣π1:t−1,s)是一个由参数 θ \theta θ参数化的单步分配策略。
四、学习协作策略
0.基础
本节描述了一种新的分层问题解决策略,称为学习协同策略(learning collaborative policies, LCP),它可以使用播种过程和修正过程这两个层次步骤有效地找到接近最优的解决方案(详见图1)。在播种过程中,播种策略 p S p^S pS生成 M M M个不同的候选解。在修正过程中,修正策略 p R p^R pR重写每个候选解 I I I次,以使候选解的行程长度最小化。然后从 M M M个修订(更新)的候选解决方案中选择最终解决方案作为最佳解决方案。请参阅附录A .4中的伪代码以获得详细的技术说明。

1.播种过程
(0)基础
播种器产生尽可能多样化的候选解决方案,同时致力于探索完整的组合行动空间。为此,需要训练播种器来解决以下问题。
(1)解决方案空间
播种器的解决方案空间是一套全轨迹的解决方案: { π ( 1 ) , … , π ( M ) } \left\{\pi^{(1)}, \ldots, \pi^{(M)}\right\} {π(1),…,π(M)}。 M M M是从播种器而来的候选解决方案:被称为样本宽度。
(2)策略结构
播种者是一种构造政策,如第3节的定义如下: p S ( π ∣ s ) = ∏ t = 1 t = N p θ S ( π t ∣ π 1 : t − 1 , s ) p^S(\boldsymbol{\pi} \mid \boldsymbol{s})=\prod_{t=1}^{t=N} p_{\theta^S}\left(\pi_t \mid \boldsymbol{\pi}_{1: t-1}, \boldsymbol{s}\right) pS(π∣s)=t=1∏t=NpθS(πt∣π1:t−1,s)
片段策略 p θ S ( π t ∣ π 1 : t − 1 , s ) p_{\theta^S}\left(\pi_t \mid \boldsymbol{\pi}_{1: t-1}, \boldsymbol{s}\right) pθS(πt∣π1:t−1,s)由 θ S \theta^S θS参数化,起源于AM模型。
(3)熵奖励
为了迫使播种器策略 p S p^S pS采样多样化的解决方案,本文训练了 p S p^S pS,使 p S p^S pS的熵 H \mathcal{H} H最大化。为此,我们使用奖励 R S R^S RS,定义为式子(1):
R S = H ( π ∼ ∏ t = 1 t = N p θ S ( π t ∣ π 1 : t − 1 , s ) ) ≈ ∑ t = 1 N w t H ( π t ∼ p θ S ( π t ∣ π 1 : t − 1 , s ) ) R^S=\mathcal{H}\left(\boldsymbol{\pi} \sim \prod_{t=1}^{t=N} p_{\theta^S}\left(\pi_t \mid \boldsymbol{\pi}_{1: t-1}, \boldsymbol{s}\right)\right) \approx \sum_{t=1}^N w_t \mathcal{H}\left(\pi_t \sim p_{\theta^S}\left(\pi_t \mid \boldsymbol{\pi}_{1: t-1}, \boldsymbol{s}\right)\right) RS=H(π∼t=1∏t=NpθS(πt∣π1:t−1,s))≈t=1∑NwtH(πt∼pθS(πt∣π1:t−1,s))
构造策略的熵适用于测量解决方案的多样性。然而,由于搜索空间太大,很难计算构造策略的熵: N ! N! N!。因此,将其近似为在不同时间步长下计算的分段策略 p θ s ( π t ∣ π 1 : t − 1 , s ) p_{\theta^s}\left(\pi_t \mid \boldsymbol{\pi}_{1: t-1}, \boldsymbol{s}\right) pθs(πt∣π1:t−1,s)的熵的加权和。
本文使用线性调度器(时变权值) w t = N − t N w w_t=\frac{N-t}{N_w} wt=NwN−t来促进在构成解决方案的早期阶段的探索;在早期阶段,较高的权重 w t w_t wt所施加的更高的随机性往往会在后期产生更多样化的完整轨迹。 N w N_w Nw是归一化因子,它是一个超参数。
(4)训练方案
为了训练播种器,本文使用了Kool等人引入的推出基线 b b b的REINFORCE算法。然后将各目标函数的梯度表示为:
∇ J ( θ S ∣ s ) = E π ∼ p S [ ( L ( π ∣ s ) − α R S ( p 1 : N S , π ) − b ( s ) ) ∇ log ( p S ) ] \nabla J\left(\theta^S \mid s\right)=E_{\pi \sim p^S}\left[\left(L(\boldsymbol{\pi} \mid s)-\alpha R^S\left(p_{1: N}^S, \boldsymbol{\pi}\right)-b(s)\right) \nabla \log \left(p^S\right)\right] ∇J(θS∣s)=Eπ∼pS[(L(π∣s)−αRS(p1:NS,π)−b(s))∇log(pS)]
请注意, α α α是 R S R^S RS的超参数,而 p 1 : N S p^S_{1:N} p1:NS是线段策略 { p θ S ( π t ∣ π 1 : t − 1 , s ) } t = 1 N \left\{p_{\theta^S} \left(\pi_t \mid \boldsymbol{\pi}_{1: t-1}, \boldsymbol{s}\right)\right\}_{t=1}^N {pθS(πt∣π1:t−1,s)}t=1N的序列。本文使用ADAM 优化器来获得使目标函数最小化的最优参数 θ ∗ θ^∗ θ∗。
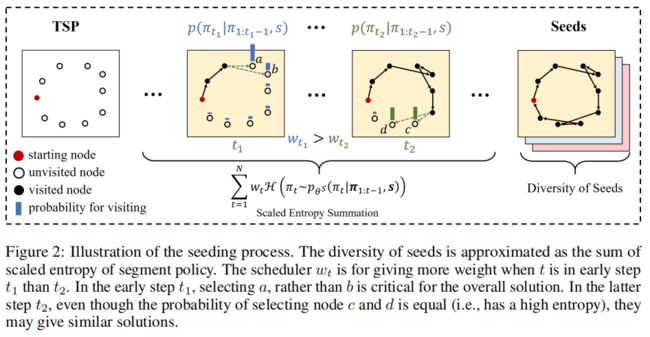
2.修订流程
(0)基础
在修正过程中,给定一个候选解,修正器将候选解分解为 K K K个段,同时为每个候选解的每个段找到最优路由序列。修正器重复这个修改过程,以找到最佳更新的候选解决方案。具体来说,修正器通过重复地将前一次迭代计算的完整轨迹分解为分段,并修改分段以生成 M M M个更新的全轨迹解,修正者依次更新候选解决方案( I I I次)。综上所述,修正器并行求解 M × K M×K M×K段( M M M:候选解的个数, K K K:每个候选解中的段的个数), I I I次串联。
该方案比传统的局部搜索方法和基于DRL的改进启发式方法具有优势。它在一个推理中搜索更大的解空间;因此,它减少了迭代 I I I。例如,2-opt和DRL-2选择搜索 O ( N 2 ) O(N^2) O(N2)解空间(如果它是可并行的 O ( M N 2 ) O(MN^2) O(MN2)),而修正器搜索 O ( M K × l ! ) O(MK×l!) O(MK×l!)在单个推理中要大得多(当段 l l l的节点数量足够大时)。因此,与2-opt或DRL-2opt相比,本文方法可以显著减少迭代次数 I I I,从而加快解决方案搜索的速度(见附录E)。
(1)解决方案空间
修正器的解空间是全轨迹解的部分片段,用 π k + 1 : k + l π_{k+1:k+l} πk+1:k+l表示。 k k k是起始索引, l l l是该段的节点数。关于分配段包括 k k k和 l l l的详细信息,请参见附录A.3。
(2)策略结构
修正器是一个构造政策如下: p R ( π k + 1 : k + l ∣ s ) = ∏ t = 1 t = l p θ R ( π k + t ∣ π k : k + t − 1 , π k + l + 1 , s ) p^R\left(\boldsymbol{\pi}_{k+1: k+l} \mid \boldsymbol{s}\right)=\prod_{t=1}^{t=l} p_{\theta^R}\left(\pi_{k+t} \mid \boldsymbol{\pi}_{k: k+t-1}, \pi_{k+l+1}, \boldsymbol{s}\right) pR(πk+1:k+l∣s)=t=1∏t=lpθR(πk+t∣πk:k+t−1,πk+l+1,s)
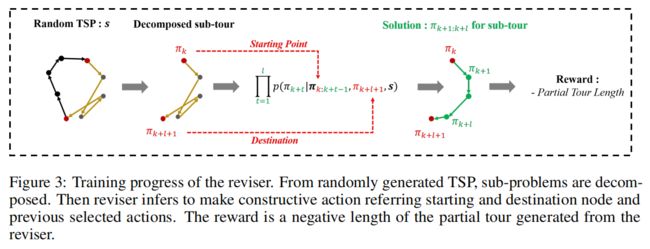
由 θ R θ^R θR参数化的分段策略 p θ R p_{θ^R} pθR与AM的形式相似。每个 π k π_k πk和 π k + l + 1 π_{k+l+1} πk+l+1分别表示部分片段的起点和目的点(见图3中的红点)。
本文修改AM的上下文嵌入向量 h ( c ) ( N ) = [ h ˉ ( N ) , h π t − 1 ( N ) , h π 1 ( N ) ] h_{(c)}^{(N)}=\left[\bar{h}^{(N)}, h_{\pi_{t-1}}^{(N)}, h_{\pi_1}^{(N)}\right] h(c)(N)=[hˉ(N),hπt−1(N),hπ1(N)],用于求解TSP问题。因此, h h h为基于变压器编码器的高维嵌入向量, N N N为多头注意层数。 h ˉ ( N ) \bar{h}^{(N)} hˉ(N)是整个嵌入的平均值, h π t − 1 ( N ) h_{\pi_{t-1}}^{(N)} hπt−1(N)是之前选定节点的嵌入, h π 1 ( N ) h_{\pi_1}^{(N)} hπ1(N)是第一个节点的嵌入。但是,由于修正器的目的地是 π k + l + 1 \pi_{k+l+1} πk+l+1,而不是第一个节点 π 1 π_1 π1,因此将上下文嵌入更改为 h ( c ) ( N ) = [ h ˉ ( N ) , h π k + t − 1 ( N ) , h π k + l + 1 ( N ) ] h_{(c)}^{(N)}=\left[\bar{h}^{(N)}, h_{\pi_{k+t-1}}^{(N)}, h_{\pi_{k+l+1}}^{(N)}\right] h(c)(N)=[hˉ(N),hπk+t−1(N),hπk+l+1(N)]。
(3)修订奖励
部分路程长度的负值 L R ( π k + 1 : k + l ∣ s ) = ∑ t = 1 l + 1 ∥ x π k + t − x π k + t − 1 ∥ 2 L^R\left(\boldsymbol{\pi}_{k+1: k+l} \mid \boldsymbol{s}\right)=\sum_{t=1}^{l+1}\left\|x_{\pi_{k+t}}-x_{\pi_{k+t-1}}\right\|_2 LR(πk+1:k+l∣s)=∑t=1l+1∥xπk+t−xπk+t−1∥2
(4)训练方案
训练过程与第4.1节基本相同,只是将长度项 L L L修改为 L R L^R LR,并设置 α = 0 α = 0 α=0来删除训练修正者的熵奖励 R S R^S RS。请注意,播种器和修正器是单独训练的。
五、实验
0.基础
(0)基础
本节报告了LCP方案在TSP、PCTSP和CVRP上的实验结果2( N = 20 , 50 , 100 , 500 N=20,50,100,500 N=20,50,100,500, N N N:节点数)。此外,本文在第5.3节和附录B-F中报告了几项消融研究。本文在附录G中评估了TSPLIB中real-world TSPs的性能。
(1)训练超参数
在播种器和修正器的整个训练过程中,本方法有与Kool等人完全相同的超参数,除了播种器的训练批量大小为1024。为了训练播种器的策略,使得下式(2),
α = 0.5 \alpha =0.5 α=0.5
以及线性权重 N w = ∑ i = 1 N i N_w=\sum^N_{i=1}i Nw=∑i=1Ni,熵调度 w t = N − t N w w_t=\frac{N-t}{N_w} wt=NwN−t。
实验设置中的细节,包括超参数、数据集配置和运行时间评估,在附录A.5中描述。
1.目标问题和基线
(0)基础
本文评估LCP解决TSP、PCTSP和CVRP三个路由问题中的性能。本文提供了一个简要的解释。对这些问题的详细描述见附录A.1。
(1)旅行商问题TSP
TSP是寻找给定节点序列最短哈密顿循环的问题。
(2)价值收集旅行商问题PCTSP
PCTSP是一个问题,其中每个节点都有一个奖励和一个惩罚。目标是收集至少具有最小总奖励(约束)的节点,并尽量减少添加有未访问节点的惩罚的旅行长度。
(3)能力有限的车辆路由问题CVRP
CVRP是一个问题,即每个节点都有一个需求,而当超过总需求限制(约束)时,车辆必须终止行程。目的是尽量减少旅行的长度。
(4)具体方法
对于基线算法,本文使用两种类型的算法:传统的启发式算法和基于DRL的求解器。对于传统的启发式方法,本文使用Gurobi(商业优化求解器)和ORTools(商业优化求解器)来解决所有这三个问题。在表1中, G u r o b i ( t ) Gurobi(t) Gurobi(t)表示运行时间限制在 t t t以下的有时间限制的Gurobi。此外, O R T o o l s ( t ) OR Tools(t) ORTools(t)是允许在 t t t的持续时间内进行额外的本地搜索的OR工具。对于特定问题的启发式,我们TSP使用Concorde,PCTSP使用迭代局部搜索(ILS),CVRP使用LKH3。
对于使用基于DRL的求解器的基线,本文集中关注LCP方案的能力,它比AM性能更高。验证双策略协作方案优于单策略方案(即AM)是本研究的关键部分;因此,性能评估的最重要指标是在普通AM和AM + LCP之间的改进。此外,本文还复制了其他竞争性的DRL框架:当前新兴的改进启发式算法。本文排除了最近提出的AM风格的构造启发式方法,包括POMO和MDAM ,因为它们可以是LCP的候选合作者,而不是竞争对手(例如,POMO + LCP是可能的)。表1中评价基线的详细方法描述如下:
TSP
本文遵循Kool等和Costa等的基线设置。本文设置了DRL基线,包括S2V-DQN、EAN、GAT-T 、DRL-2opt和AM。本文展示了Kool等报道的S2V-DQN和EAN的结果,以及Costa等报道的GAT-T的结果。然后,本文在作者的机器中直接复制基线之间最具竞争的两个DRL框架,AM和DRL-2opt,以对速度进行公平的比较。
PCTSP
本文遵循Kool等人的的基线设置。重现了DRL基线的AM 。
CVRP
本文遵循Houttung & Tierney的基线设置。报告了基于Houttung & Tierney的RL 的结果,并复刻了AM 和NLNS。
2.表现评估
(0)基础
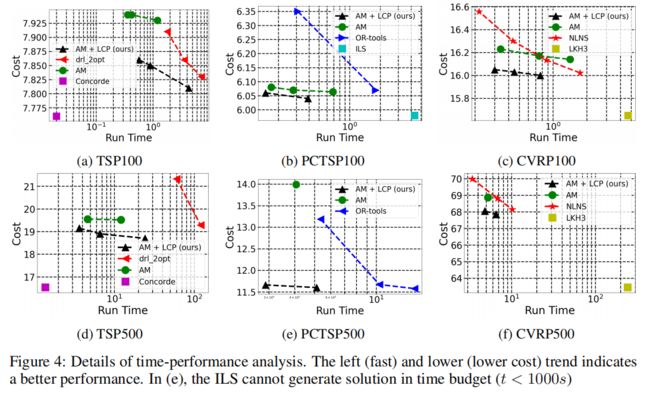
在本节中,本文将在表1中报告LCP在小规模问题( N = 20 , 50 , 100 N = 20,50,100 N=20,50,100)上的性能。然后本文提供了一个包括大规模问题( N = 500 N = 500 N=500)。作者注意到时间性能分析是重要的,因为当给定无限时间预算时,任何方法都能找到最优解。从分析中,可以确定一个特定的时间区域,称为赢家区域(winner region),在那里LCP在速度和性能方面都表现最好。
(1)表现评估 N = 20, 50, 100
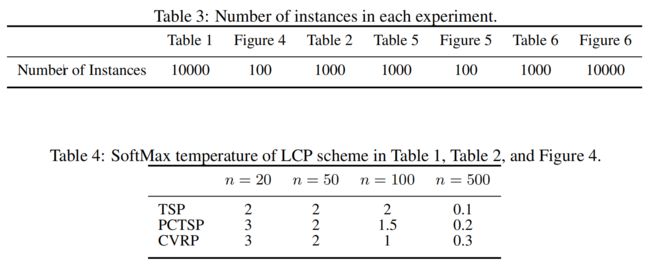
本文的方法在TSP、PCTSP和CVRP中优于所有的DRL基线和or工具,如表1所示。
注意,对于TSP( N = 100 N = 100 N=100),本文应用了两种类型的修正器,每一种都分别记为LCP和LCP*。这些细节在附录A.4中使用伪代码进行了描述。本文的LCP和LCP*优于DRL-2opt,既目前最先进的基于DRL的改进启发式在 N = 20 , 50 , 100 N = 20,50,100 N=20,50,100,在 N = 100 N = 100 N=100中超过0.33%。
在PCTSP中,LCP在更短的时间下优于AM。本文的方法(AM + LCP {640,1})优于OR-Tools(10s),在 N = 50 , 100 N = 50,100 N=50,100时的速度分别快 4 × 4× 4×和 2 × 2× 2×。与ILS相比,本文的方法(AM + LCP {1280,5})的性能差1.0%,但对 N = 100 N = 100 N=100的速度快了 11 × 11× 11×。
对于CVRP,我们的方法优于具有竞争力的DRL框架。
(2)时间表现分析 N = 100, 500
在图4中,本文描述了时间-性能分析。作者无法控制Concorde、ILS和LKH3的速度。作者可以通过调整样本宽度 M M M或迭代次数 I I I来控制DRL求解器的速度。对于PCTSP,作者可以通过管理额外本地搜索的时间来改变OR工具的速度。
本文的方案在速度和性能方面都明显优于DRL-求解器。对于PCTSP( N = 100 , 500 N = 100,500 N=100,500)和CVRP( N = 500 N = 500 N=500),本文的方法获得了 t < 10 t < 10 t<10的赢家区域,这在所有基线求解器的特定时间区域中表现最好(对于CVRP( N = 100 N = 100 N=100),本文的方法获得了 t < 5 t<5 t<5的赢家区域)。
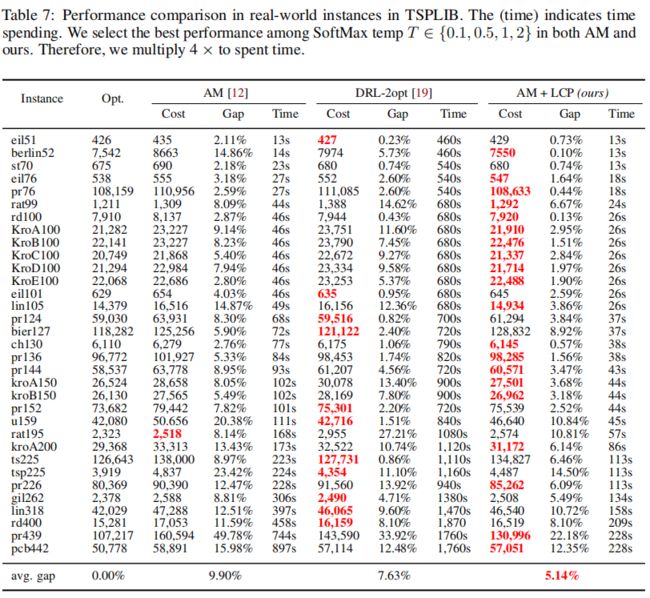
(3)TSPLIB的表现
见附录G。
3.消融研究
(0)基础
在本节中,作者将对LCP成分进行消融研究。本文将进一步的消融研究留给了附录B-F。
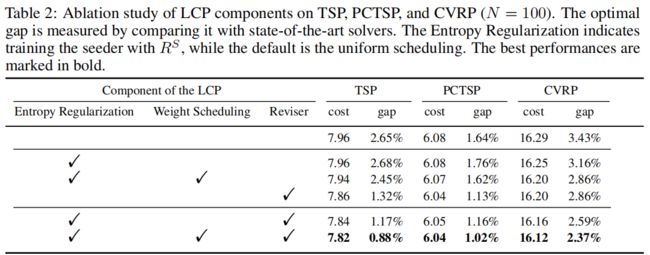
(1)合作政策的消融研究
在表2中,作者消融了LCP的三个重要成分,并显示了每个病例的实验结果。在普通AM中,没有任何LCP组件,性能最差。另一方面,用线性调度熵训练的播种器和修正器的协作效果最好。因此,实验结果实证验证了本文提出的两种策略分层协作的建议,也证明了使用第4.1节和图2节中所示的线性调度熵项的有效性。
(2)附录信息
熵正则化的消融研究:见附录 B.
SoftMax temperature的消融研究:见附录 C.
LCP在指针网络中的消融研究:见附录 D.
与修正器和其他改进启发式的比较:见附录E.
不同PyTorch种子中的训练收敛性:见附录F。
六、讨论
(0)基础
在本文中,作者提出了一种新的DRL方案,即学习协作策略(LCP)。大量的实验表明,本文的双策略协作算法(即LCP)在各种TSP、PCTSP和CVRP等np困难路由问题上优于传统的单策略DRL框架,包括AM。
作者强调,LCP是一个可重用的方案,可以解决各种问题。本文提出的播种器和修正器的神经结构来自于AM。它可以被其他体系结构所取代,如指针网络和AM风格的体系结构,包括POMO 和MDAM。如果对组合优化的神经结构进行进一步的研究,可以进一步改进播种器。
此外,LCP可以直接应用于其他组合优化任务,包括带时间窗的TSP(TSPTW)、定向问题(OP)、多重TSP(mTSP)、车辆路径问题(VRP)等实际应用。
(1)未来工作
本文迈出了重要的第一步:双策略协作,其中每个专门从事探索或开发的策略都可以改进组合优化任务上的传统单策略系统。进一步研究的重要方向是引入更复杂的策略来探索或利用组合解空间。需要新的探索策略来克服所提出的近似熵最大化策略。此外,有必要在拟议的修订方案之外研究更有效的开发策略。
七、附录
A 实验细节
A.1 对目标问题的详细说明
本文解决了三个NP-hard路径问题:旅行商问题(TSP)、奖励收集TSP(PCTSP)和有限容量车辆路径问题(CVRP)。本节提供了PCTSP和CVRP的详细描述(对于TSP,见第3节)。
PCTSP
PCTSP与TSP相似,但不同之处在于,我们不必访问所有的节点,目的地不是第一个节点,而是仓库节点,即访问不是一个循环。设 N N N为节点数。PCTSP的问题实例是 s = { ( x i , λ i , μ i ) } i = 1 N + 1 \boldsymbol{s}=\left\{\left(x_i, \lambda_i, \mu_i\right)\right\}_{i=1}^{N+1} s={(xi,λi,μi)}i=1N+1,其中 x i ∈ R 2 x_i \in \mathbb{R}^2 xi∈R2在二维欧几里得坐标中, λ i ∈ R \lambda_i \in \mathbb{R} λi∈R是未访问节点的惩罚, μ i ∈ R \mu_i \in \mathbb{R} μi∈R是被访问节点的奖励。
f ( π ∣ s ) = L ( π ∣ s ) + λ ( π ∣ s ) L ( π ∣ s ) = ∑ i = 1 k ∥ x π i − x π i − 1 ∥ 2 + ∥ x π 1 − x n + 1 ∥ 2 + ∥ x π k − x n + 1 ∥ 2 λ ( π ∣ s ) = ∑ i ∉ π λ i \begin{aligned} &f(\boldsymbol{\pi} \mid \boldsymbol{s})=L(\boldsymbol{\pi} \mid \boldsymbol{s})+\lambda(\boldsymbol{\pi} \mid \boldsymbol{s})\\ &\begin{gathered} L(\boldsymbol{\pi} \mid \boldsymbol{s})=\sum_{i=1}^k\left\|x_{\pi_i}-x_{\pi_{i-1}}\right\|_2+\left\|x_{\pi_1}-x_{n+1}\right\|_2+\left\|x_{\pi_k}-x_{n+1}\right\|_2 \\ \lambda(\boldsymbol{\pi} \mid \boldsymbol{s})=\sum_{i \notin \pi} \lambda_i \end{gathered} \end{aligned} f(π∣s)=L(π∣s)+λ(π∣s)L(π∣s)=i=1∑k∥xπi−xπi−1∥2+∥xπ1−xn+1∥2+∥xπk−xn+1∥2λ(π∣s)=i∈/π∑λi
L ( π ∣ s ) L(\boldsymbol{\pi} \mid \boldsymbol{s}) L(π∣s)是行程长度, λ ( π ∣ s ) \lambda(\boldsymbol{\pi} \mid \boldsymbol{s}) λ(π∣s)是未访问节点的总惩罚。 k = ∣ π ∣ k=|\pi| k=∣π∣, k ≤ N k \leq N k≤N,因为整个旅程并不包含所有的节点。最低奖励 μ ( c ) \mu_{(c)} μ(c)的约束条件如下式(3):
∑ i ∈ π μ i ≥ μ ( c ) \sum_{i \in \pi} \mu_i \geq \mu_{(c)} i∈π∑μi≥μ(c)
大部分的MDP与TSP相似,包括培训方案。与TSP不同,在满足约束(3)之前,存在禁止选择仓库节点 π N + 1 \pi_{N+1} πN+1上的动作的限制。我们将问题实例s中的解(动作序列)的累积奖励定义为 R = R f + α R S R=R_f+\alpha R^S R=Rf+αRS,其中 R f = − f R_f =−f Rf=−f, R S R^S RS是第4.1节中的熵奖励, α α α是一个超参数。
CVRP
在CVRP中,当车辆超过最大需求 v ( c ) v_{(c)} v(c)时,车辆不能再访问节点。因此,车辆必须返回到仓库节点,并开始另一次旅行。车辆可以进行 k k k次旅行, π = { π ( i ) } i = 1 k \boldsymbol{π} = \{\boldsymbol{π}_{(i)}\}^k_{i=1} π={π(i)}i=1k,其中每个子旅行(子排列)的第一个和最后一个元素π(i)是仓库节点。设N为节点数。然后将CVRP的实例表示为 s = { ( x i , v i ) } i = 1 N + 1 s=\left\{\left(x_i, v_i\right)\right\}_{i=1}^{N+1} s={(xi,vi)}i=1N+1,其中仓库节点为 s n + 1 = ( x n + 1 , 0 ) s_{n+1}=\left(x_{n+1}, 0\right) sn+1=(xn+1,0)。CVRP的目标是最小化 f f f:
f ( π ∣ s ) = ∑ i = 1 k ∑ j = 1 l i ∥ x π ( i ) j − x π ( i ) j − 1 ∥ 2 f(\pi \mid s)=\sum_{i=1}^k \sum_{j=1}^{l_i}\left\|x_{\pi_{(i)_j}}-x_{\pi_{(i)_{j-1}}}\right\|_2 f(π∣s)=i=1∑kj=1∑li xπ(i)j−xπ(i)j−1 2
其中 l i = ∣ π ( i ) ∣ l_i=\left|\pi_{(i)}\right| li= π(i) 。对于每段路程 π ( i ) \pi_{(i)} π(i), 它们是对最大需求的限制 v ( c ) v_{(c)} v(c) :
∑ j ∈ π ( i ) v j ≤ v ( c ) \sum_{j \in \pi_{(i)}} v_j \leq v_{(c)} j∈π(i)∑vj≤v(c)
MDP的配方与TSP基本相同。存在基于约束(4)的动作限制规则,当超过最大需求时(即当选择仓库节点时违反(4)),选择仓库节点以外的每个动作都受到限制。
与PCTSP类似,我们的奖励是 R = R f + α R S R = R_f + αR^S R=Rf+αRS,其中 R f = − f R_f =−f Rf=−f。政策结构和培训方案同TSP相同。
A.2 推理阶段的详细实现
本节提供了实验中播种器的实现细节。我们的播种器 p S p^S pS是由AM参数化的,这是基于Transformer的编码器-解码器模型。关于AM架构的细节,请参见Kool等人。
SoftMax temperature
AM体系结构的输出是对所有节点 u ( c ) u_{(c)} u(c)的查询的兼容性(见Kool等人中的(7))。然后用SoftMax函数表示选择节点的概率如下:
p θ S ( π t = i ∣ π 1 : t − 1 , s ) = SoftMax ( u ( c ) , i , T ) SoftMax ( u ( c ) , i , T ) = e u ( c ) i T ∑ j e u ( c ) j T \begin{gathered} p_{\theta^S}\left(\pi_t=i \mid \boldsymbol{\pi}_{1: t-1}, \boldsymbol{s}\right)=\operatorname{SoftMax}\left(u_{(c)}, i, T\right) \\ \operatorname{SoftMax}\left(u_{(c)}, i, T\right)=\frac{e^{\frac{u_{(c) i}}{T}}}{\sum_j e^{\frac{u_{(c) j}}{T}}} \end{gathered} pθS(πt=i∣π1:t−1,s)=SoftMax(u(c),i,T)SoftMax(u(c),i,T)=∑jeTu(c)jeTu(c)i
SoftMax temperature T T T是播种器采样的一个重要超参数。注意,如果 T ≈ 0 T≈0 T≈0,那么 p θ S ( π t = i ∣ π 1 : t − 1 , s ) p_{θ^S}(π_t=i|π_{1:t−1},s) pθS(πt=i∣π1:t−1,s)将选择贪婪的样本:即 π t = arg max ( p θ S ( π t = i ∣ π 1 : t − 1 , s ) ) π_t=\argmax(p_{θ^S}(π_t=i|π_{1:t−1},s)) πt=argmax(pθS(πt=i∣π1:t−1,s))。如果是 T ≈ ∞ T≈∞ T≈∞,它将与随机搜索相同。在训练阶段,作者设置为 T = 1 T = 1 T=1。在推理阶段(即在实验中)设置 T T T的细节见附录A.5。
A.3 修正器的详细实施情况
本节描述了针对每个目标问题的修正器的详细实现。
TSP
让修正器 ( L ) (L) (L)在带有 L L L个节点的TSP上进行训练。在训练阶段,限制选择起始节点和结束节点,因此 L − 2 L−2 L−2节点处于动作空间中。
在推理阶段,段的长度(动作空间中的节点数) l = L − 2 l=L−2 l=L−2( − 2 -2 −2是因为开始和结束节点受到限制),段数 K = N / L K = N/L K=N/L( N N N:来自播种者的种子节点数)。每个段的起点表示为 { k , k + L , k + 2 L , . . , } \{k,k+L,k+2L,..,\} {k,k+L,k+2L,..,},其中每个段彼此不相交。
修正器通过重新分配 1 ≤ k ≤ l 1≤k≤l 1≤k≤l来重复修改过程。在实验中,我们简单地迭代分配 k i = ( k i − 1 + 1 ) ki=(ki−1+1) ki=(ki−1+1), 1 ≤ i ≤ I 1≤i≤I 1≤i≤I。详见算法1。
设我为修订过程的迭代次数。对于表1中的LCP*,我们使用了校正器(10)。对于表1中的 L C P ∗ LCP* LCP∗、附录G中的TSPLIB实验和大规模TSP( N = 500 N = 500 N=500),我们使用了校正器(20)( I = 25 I = 25 I=25)和校正器(10)( I = 20 I = 20 I=20),详见算法2。
对于CVRP和PCTSP,有仓库节点,我们不需要额外的进程来使修正器,而不像TSP的仓库节点本身是起始节点。因此,我们可以使用播种器(没有熵奖励)作为修正器。我们注意到,VRP变体的其他问题,TSP变体是简单的播种器的轻微变化。此外,大多数问题也可以由TSP修改者进行修改。
PCTSP
对于小规模问题( N = 20 , 50 , 100 N = 20,50,100 N=20,50,100),播种器生成种子(中间解决方案)后,修正器不会选择未访问节点或删除访问节点。也就是说,被访问节点的选择是固定的,修正器只调整被访问节点的顺序。因此,我们在修正器中使用(10)进行小规模实验。该分解规则与TSP相同。
对于大规模问题( N = 500 N = 500 N=500),我们设置了 K = 5 , L = 100 K = 5, L = 100 K=5,L=100。我们使用在PCTSP( N = 100 N = 100 N=100)中训练的播种器作为大规模任务的修正器。
CVRP
对于小规模的问题( N = 20 , 50 , 100 N = 20,50,100 N=20,50,100),我们使用了带有 K = 10 K = 10 K=10的校正器(10)。对于大规模的问题( N = 500 N = 500 N=500),我们使用在CVRP( N = 100 N = 100 N=100)上训练的播种机作为校正器。我们设置了 K = 2 K = 2 K=2和 N = 250 N = 250 N=250。
CVRP的解决方案具有子行程 π ( i ) π_{(i)} π(i);各段的起点与子行程的起点相同。对于并行化(使段长度相同),当子路中的节点数小于分配的段长度 L L L时,我们创建填充节点(仓库节点)。
A.4 LCP算法细节
本节提供了第4节和附录A.3的基于伪代码的解释,以明确理解。算法1用于单修正器,算法2用于双修正器(修正器1,修正器2)。这些算法主要针对TSP;对PCTSP和CVRP的应用基本相似(分解方法有所不同),如附录A.3所述。

A.5 实验设置细节
数据集
本文遵循Kool等人在中介绍的方法,基于所提供的代码,随机生成TSP、PCTSP和CVRP的数据集。
运行时间对比
所有的实验都使用了单个GPU(NVIDIA RTX 2080 Ti)和单个CPU(Intel i7-9700K);很少有例外。表1中的启发式求解器的速度来自Kool等人的,其中它是使用两个cpu(2×Xeon E5-2630)执行的。
第5节中描述的所有运行时间都是每个实例的平均时间。对于表1中的运行时间测量,直接用作者的机器复刻了AM和DRL-2opt。DRL-2opt的实现是基于Costa等人提供的代码。NLNS的结果来自代码,其他的来自Kool等人的。
例如,启发式方法主要在CPU中执行,而DRL框架则在GPU中执行。GPU的并行化能力通常高于CPU。因此,DRL框架将在高 B B B中显示出快速的速度。
此外,在DRL框架之间进行公平的比较也很困难。DRL-2opt在并行化方面有其优点,但它的串行速度较慢,因为它们需要迭代推断(大约2000次迭代)。相比之下,本文的LCP方案具有快速的串行速度,因为本文的播种器只需要一个推理,而修正器需要很少的迭代。本文的修订过程对于单个实例是可并行的,因为修订器同时解决分解的种子。
对于实验,本文给出了 B ≤ 100 B≤100 B≤100的限制。因为,从实际的角度来看,10000个相同规模的实例很少同时出现,所以我们应该合理地限制评估批的大小。此外,许多现实世界的问题需要顺序解决路由问题:即,在低 B B B条件下测量速度是合适的。
对于大规模实验( N = 500 N = 500 N=500)中的运行时间测量,本文为所有基线设置为 B = 1 B = 1 B=1。除DRL-2opt和NLNS外,其余实验均在相同的CPU(Intel i7-9700K)和GPU(Nvidia RTX2080Ti)上进行。对于DRL-2opt和NLNS,作者设置了 B = 10 B=10 B=10(占实例总数的10%)。此外,请注意的是,作者基于Kool等人提供的代码,在大规模实验( N = 500 N = 500 N=500)中复制了Concorde、Gurobo、OR工具、ILS和LKH3。
温度尺度
在小尺度 N = 20 , 50 , 100 N = 20,50,100 N=20,50,100的实验中,我们将AM的SoftMax temperature T T T设为 1 1 1,这是Kool等人在中报道的默认设置。对于大规模实验 N = 500 N = 500 N=500,将AM的 T T T调为 0.1 0.1 0.1。LCP方案的 T T T设置见表4。
B 尺度熵正则化的消融研究
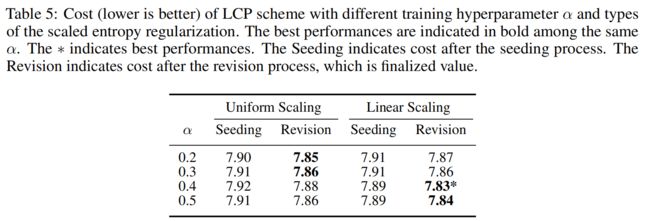
本节提供了 α α α的详细消融研究,一个尺度熵奖励 R S R^S RS的超参数。本文以TSP( N = 100 N = 100 N=100)为目标,随机生成100个实例。作者在实验中使用了带有 I = 10 I=10 I=10的修正器(10)。播种器的软最高温度 T T T固定为2。如表5所示,当 α = 0.2 , 0.3 α=0.2,0.3 α=0.2,0.3时,具有均匀尺度熵正则化的LCP的性能超过了线性尺度。然而,当 α = 0.4 , 0.5 α = 0.4,0.5 α=0.4,0.5时,具有线性尺度熵正则化的LCP优于均匀尺度,它们在所有情况下的 α = 0.2 , 0.3 , 0.4 , 0.4 , 0.5 α=0.2,0.3,0.4,0.4,0.5 α=0.2,0.3,0.4,0.4,0.5中都取得了最好的性能。
C 消融SoftMax temperature
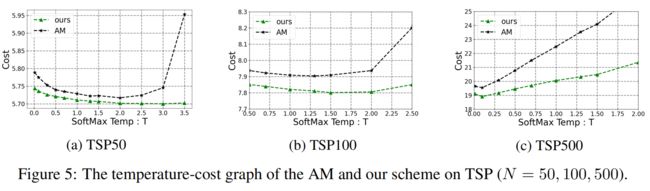
如图5所示,实验结果表明,本文的方法对温度尺度的变化具有鲁棒性,而AM则易受高温条件的影响。注意到,本文的方法的SoftMax temperature高于AM。例如,在TSP( N = 50 N = 50 N=50)中,AM在 T = 2.0 T = 2.0 T=2.0时表现最好,而本文的方法在 2.0 < T < 3.5 2.0 < T < 3.5 2.0<T<3.5时表现最好。它表明,虽然高温提供了不同的解决方案,但解决方案的质量是不够的,因为AM的适应度景观比本文的方案更陡峭。在TSP( N = 500 N = 500 N=500)中,两种方法都有一个陡峭的适应度景观;因此,非常低的温度 T = 0.1 T = 0.1 T=0.1给出了一个合理的解决方案。虽然本文的方法在大尺度上的温度稳健性具有显著的性能提高,但仍然需要一个具有更广泛的适应性的策略。
D 将LCP应用于其他DRL框架
第5节提到,本文的LCP方案可以很容易地应用于其他策略上的DRL框架。本节通过使用LCP( N = 20 N=20 N=20)中的LCP方案指针网络进行了LCP灵活性的经验验证。在实验中,播种器由指针网络参数化,而修正器的设置与之前的实验相似;作者使用修正器(10)进行5次迭代( I = 5 I = 5 I=5)。指针网络的实现基于Kool等人提供的代码,训练超参数与它们相同,除了本文设置批处理大小为 1024 1024 1024, α = 0.5 α=0.5 α=0.5。播种器的SoftMax temperature T T T固定为 1 1 1。这个包含 1000 1000 1000个实例的数据集是使用与之前的实验相同的方法随机生成的。如表6所示,使用本文的LCP的采样方法(指针网络{1280})在所有设置中都获得了最好的性能,与普通的指针网络相比,它给出了显著的性能增量。
值得注意的是,播种机的取样方法本身降低了性能。指针网络采样法的代价为7.33,而贪心法的代价为3.95。而在使用LCP时,采样方法的代价大大降低,即使LCP支持贪心方法,最终也超过了贪心方法。这表明,LCP修改不同种子的主要思想对指针网络具有广阔的应用前景。即使取样的1280颗种子不是合理的解决方案,具有多样性的种子也会被平行修改。最终,修改后的种子中最好的解决方案具有突出的性能。

E 与修正器和改进启发式的比较
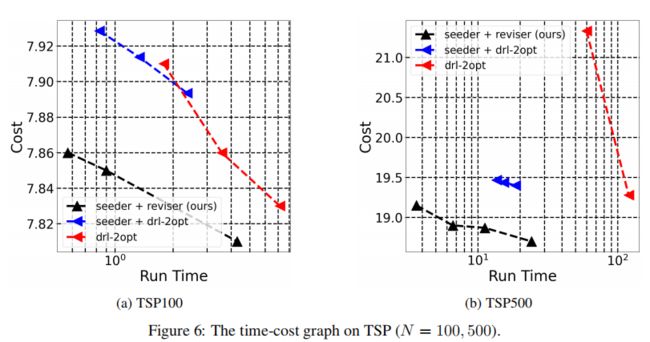
本实验是为了测试修正器的性能。播种器+修正器在时间和性能上都优于播种器+DRL-2选择。实验结果表明,该算法在快速、准确的改进启发式作用下表现良好。由于通过适当地修改播种器可以很容易地设计出修正器,因此当提出一种新型的播种机(构造启发式)时,可以相应地创建一个高性能的改进启发式(即修正器)。
F 不同PyTorch种子训练收敛的实验
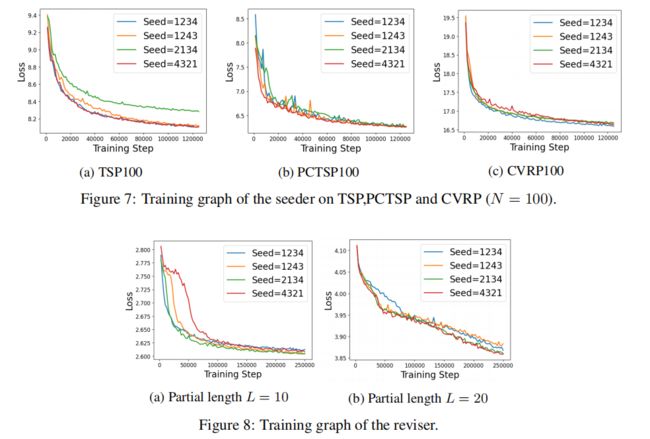
实验验证了所提出的播种机和校正机在各种PyTorch种子中收敛。DRL算法在收敛到随机种子时有时不稳定;因此,用随机种子进行实验是至关重要的。通过这个实验,我们可以看到播种机和校正机在4个随机种子中稳定收敛。
G 关于TSP的Real World实验的细节
本实验评估了从TSPLIB中提取的35个实例上的求解器的性能。本实验考虑了求解器在现实问题中的性能,并测试了在固定尺度( N = 100 N = 100 N=100)上训练的模型在不同尺度实例下的适合程度。
在本实验中,我们分别用校正器(20)( I = 25 I = 25 I=25)、校正器(10)( I = 20 I = 20 I=20)和样本宽度 M = 2560 M = 2560 M=2560进行了实验。作者将AM的样本宽度设置为 M = 40000 M=40000 M=40000,DRL-2opt的迭代次数设置为 I = 2000 I = 2000 I=2000。
在35个案例中,有22例优于基线求解器,平均最优间隙优于Drl-2opt2.5%。与DRL-2opt和AM相比,它的速度也要快得多。