JavaScript实现树结构

一、二叉搜索树的封装

 二叉树搜索树的基本属性：

 如图所示：二叉搜索树有四个最基本的属性：指向节点的根（root），节点中的键（key）、左指针（right）、右指针（right）。

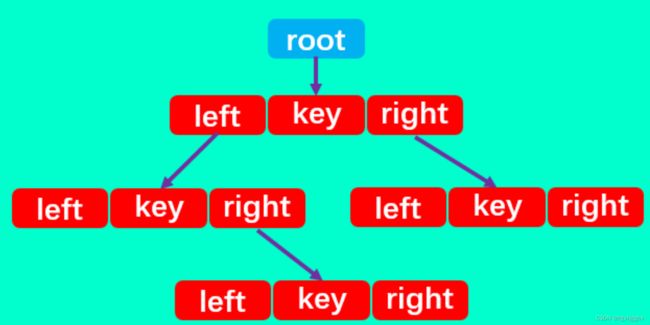 所以，二叉搜索树中除了定义root属性外，还应定义一个节点内部类，里面包含每个节点中的left、right和key三个属性：

 //封装二叉搜索树
    function BST() {
      //
      function NOde(key) {
        this.key = key
        this.left = null
        this.right = null
      }
      //属性

      this.root = null
}

 二叉树的常见操作：

• insert（key）：向树中插入一个新的键；
• search（key）：在树中查找一个键，如果节点存在，则返回true；如果不存在，则返回false；
• inOrderTraverse：通过中序遍历方式遍历所有节点；
• preOrderTraverse：通过先序遍历方式遍历所有节点；
• postOrderTraverse：通过后序遍历方式遍历所有节点；
• min：返回树中最小的值/键；
• max：返回树中最大的值/键；
• remove（key）：从树中移除某个键；

 1.插入数据

• 首先根据传入的key创建节点对象；
• 然后判断根节点是否存在，不存在时通过：this.root = newNode，直接把新节点作为二叉搜索树的根节点。
• 若存在根节点则重新定义一个内部方法insertNode（）用于查找插入点。

 //插入数据
      BST.prototype.insert = function (key) {
        //1.根据key船舰节点 
        let newNOde = new NOde(key)
        //2.判断根节点是否有值
        if (this.root == null) {
          this.root = newNOde
        }
        else {
          this.insertNode(this.root, newNOde)
        }
      }

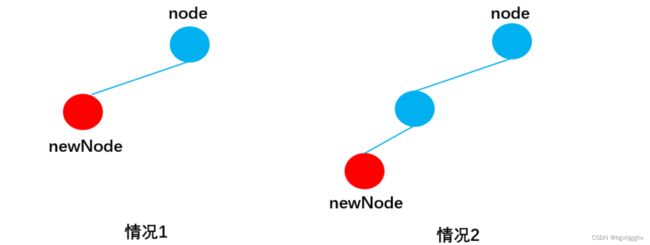
当newNode.key < node.key向左查找:

• 情况1：当node无左子节点时，直接插入：

• 情况2：当node有左子节点时，递归调用insertNode(),直到遇到无左子节点成功插入newNode后，不再符合该情况，也就不再调用insertNode()，递归停止。

 

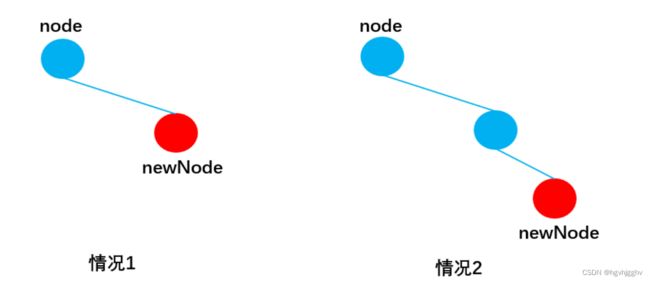
当newNode.key >= node.key向右查找，与向左查找类似：

• 情况1：当node无右子节点时，直接插入：

• 情况2：当node有右子节点时，依然递归调用insertNode(),直到遇到传入insertNode方法的node无右子节点成功插入newNode为止：

     BST.prototype.insertNode = function (node, newNOde) {
        if (newNOde.key < node.key) {//向左查找
          if (node.left == null) {
            node.left = newNOde
          }
          else {
            this.insertNode(node.left, newNOde)
          }
        }
        else {//向右查找
          if (node.right == null) {
            node.right = newNOde
          }
          else {
            this.insertNode(node.right, newNOde)

          }
        }
      }

2.遍历数据

• 先序遍历
• 中序遍历；
• 后序遍历；

先序遍历的过程为：

• 首先，遍历根节点；
• 然后，遍历其左子树；
• 最后，遍历其右子树；

//先序遍历
      BST.prototype.preorder = function (handler) {
        this.preorderBST(this.root, handler)
      }
      BST.prototype.preorderBST = function (node, handler) {
        if (node !== null) {
          //1. 处理经过的节点
          handler(node.key)
          //2.处理经过节点的左子节点
          this.preorderBST(node.left, handler)
          //3.处理经过节点的右子节点
          this.preorderBST(node.right, handler)
        }
      }

2.2.中序遍历

实现思路：与先序遍历原理相同，只不过是遍历的顺序不一样了。

• 首先，遍历其左子树；
• 然后，遍历根（父）节点；
• 最后，遍历其右子树；

 

 //2.中序遍历
      BST.prototype.minOrder = function (handler) {
        this.minNode(this.root, handler)
      }
      BST.prototype.minNode = function (node, handler) {
        if (node !== null) {
          //1.处理我门左子树的节点
          this.minNode(node.left, handler)
          //2.处理节点
          handler(node.key)
          //3.处理右子树中的节点
          this.minNode(node.right, handler)
        }
      }

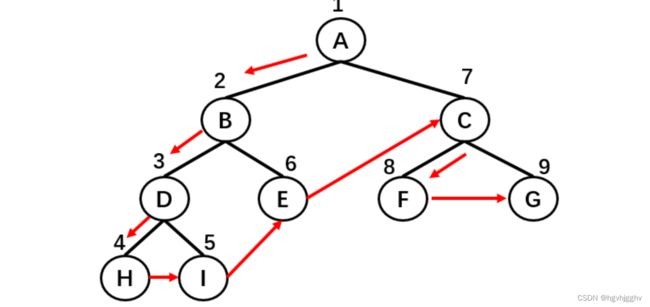
2.3.后续遍历

实现思路：与先序遍历原理相同，只不过是遍历的顺序不一样了。

• 首先，遍历其左子树；
• 然后，遍历其右子树；
• 最后，遍历根（父）节点；

过程：

  //3.后序遍历
      BST.prototype.afterder = function (handler) {
        this.afterNode(this.root, handler)
      }
      BST.prototype.afterNode = function (node, handler) {
        if (node != null) {
          //1.处理我门左子树的节点
          this.minNode(node.left, handler)
          //2.处理右子树中的节点
          this.minNode(node.right, handler)
          //3.处理节点
          handler(node.key)
        }
      }

3.查找数据

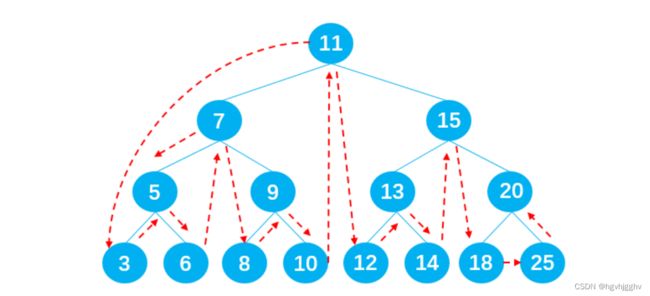
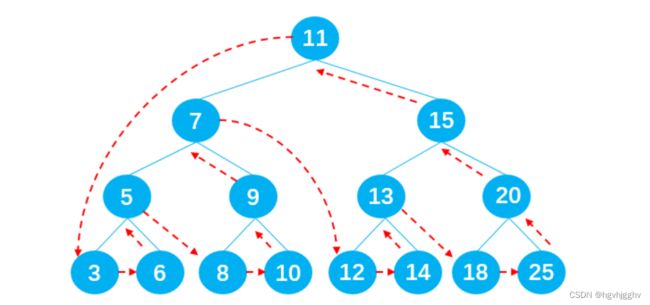
3.1查找最大值&最小值

在二叉搜索树中查找最值非常简单，最小值在二叉搜索树的最左边，最大值在二叉搜索树的最右边。只需要一直向左/右查找就能得到最值，如下图所示：