Java中的拓扑排序

Java中的拓扑排序

弗拉基米尔·巴托坎宁（VladimirBatoćanin） • 0评论

 

介绍

穿衣服时，就像您一样，您很可能没有以下思路：

哦，穿上裤子先穿好内裤可能是个好主意。

这是因为我们习惯于按拓扑对动作进行排序。或更简单地说，我们习惯于从逻辑上推断哪些动作必须在其他动作之前或之后执行，或者哪些动作是其他动作的先决条件。

 

 

例如，假设您要盖房子，步骤将如下所示：

1. 奠定基础
2. 用装置建造墙
3. 放入绝缘层
4. 摆放装饰品/门面

按照确切的顺序-这是无可争议的。如果没有地基，则无法建造墙；如果没有墙，则无法进行绝缘。

在本文中，我们将通过以下主题介绍拓扑排序的概念：

 

 

 

 

 

• 图简介
• 拓扑排序概念
• 实施拓扑排序
• 问题建模

图简介

由于拓扑排序已应用于有向非对称图（DAG），因此我们首先要谈一谈Graphs。

Graph只是一种数据结构，它表示一组具有彼此之间特定关系的对象-这些对象由节点（圆形）表示，而各个关系由边缘（线）表示。

有很多不同类型的图，但是对于眼前的问题，我们需要学习什么是有向无环图。让我们将较大的不良数学术语分解为更小，更易理解的部分。

定向的

有图有定向如果两个对象之间的每个关系并不一定是双向的（它必须有一个方向），不同于单向曲线，每一个关系已去两种方式。

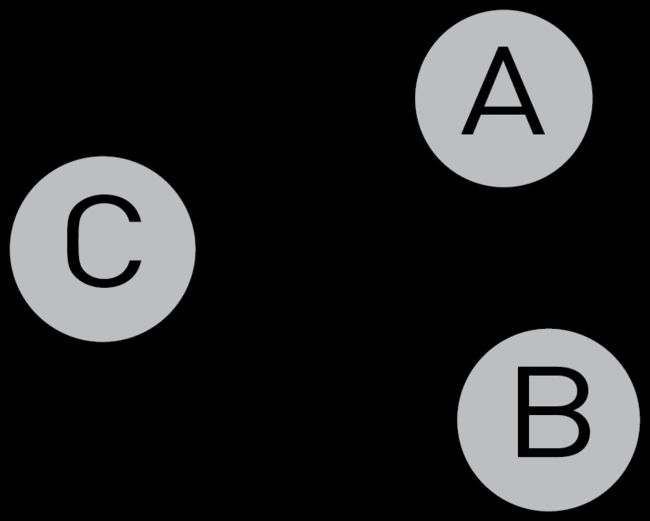
在下图中，该关系C-A是单向的，这意味着C与A和A具有关系C。

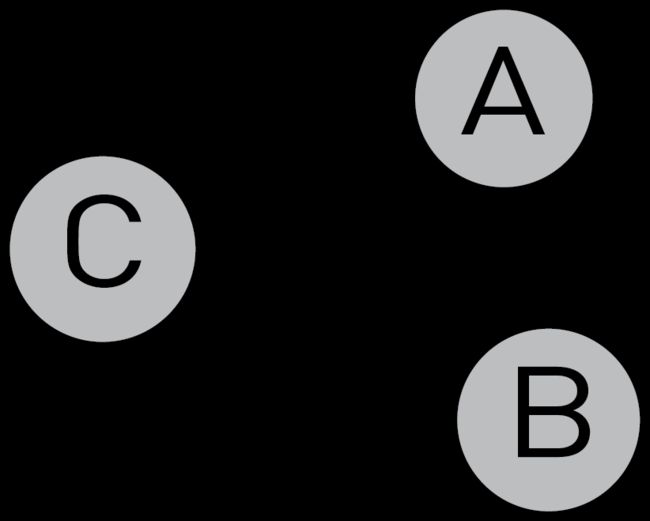
另一方面，在下图中，关系C-A是有向的，这意味着A与有关系C，但C与没有关系A。

由于存在这种差异，我们必须严格定义节点的邻居是什么：

单向图：

如果两个节点（A和B）之间存在单向路径，则它们是相邻节点。

有向图：

A是B的邻居，如果直接向边的存在，导致B对A。该定义中的第一个直接指的是以下事实：从到的路径长度必须严格为1。BA

非循环

给定图只有在不存在循环的情况下才是非循环的。循环是任何节点的路径X，始于X并返回到X。下图不是非循环的，因为它包含一个循环（X-B-C-X）。

基本拓扑排序概念

那么，在图上使用拓扑排序时，外观如何？为什么图必须是非循环的才能起作用？

为了回答这些问题，让我们严格定义对图进行拓扑排序的含义：

 

 

 

的曲线图是拓扑排序如果一个序列a1，a2，a3...的情况下（ai是图中的节点），其中，为每一个边缘ai- > aj，ai来之前aj的序列中

如果我们说动作是由节点表示的。上面的定义基本上意味着必须存在无可争议的执行顺序。

为了更好地理解拓扑排序背后的逻辑以及为什么它不能在包含循环的图上工作，我们假设我们是一台试图对以下图进行拓扑排序的计算机：

# Let's say that we start our search at node X
# Current node: X
step 1: Ok, i'm starting from node X so it must be at the beginnig of the sequence.
    sequence: [X]

# The only available edge from X is X->B, so we 'travel' to B
# Current node: B
step 2: Right, B comes after X in the sequence for sure.
    sequence: [X,B]

# We travel to C using the edge B->C
# Current node: C
step 3: Same thing as the last step, we add C.
    sequence: [X,B,C]

# Current node: X
step 4: WHAT IN THE TARNATION, X AGAIN?
    sequence: [X,B,C,X]

这就是为什么我们无法对包含循环的图进行拓扑排序的原因，因为以下两个语句都是正确的：

订阅我们的新闻

在收件箱中获取偶尔的教程，指南和作业。从来没有垃圾邮件。随时退订。

 

通讯注册

订阅

 

• X在B之前
• B在X之前

因此，我们无法确定给定动作的绝对顺序。

现在，因为我们熟悉了算法的概念，所以让我们看一下Java中的实现。

执行

首先，让我们构造用于定义节点和图的类，然后使用所述类定义以下图：

public class Graph {
    private List nodes;

    public Graph() {
        this.nodes = new ArrayList<>();
    }

    public Graph(List nodes) {
        this.nodes = nodes;
    }

    public void addNode(Node e) {
        this.nodes.add(e);
    }

    public List getNodes() {
        return nodes;
    }

    public Node getNode(int searchId) {
        for (Node node:this.getNodes()) {
            if (node.getId() == searchId) {
                return node;
            }
        }
        return null;
    }

    public int getSize() {
        return this.nodes.size();
    }

    @Override
    public String toString() {
        return "Graph{" +
                "nodes=" + nodes +
                "}";
    }
}

该图非常简单，我们可以将其实例化为空或使用一组节点，添加节点，检索它们并将其打印出来。

现在，让我们继续Node上课：

 

 

public class Node {
    private int id;
    private List neighbors;

    public Node(int id) {
        this.id = id;
        this.neighbors = new ArrayList<>();
    }

    public void addNeighbor(int e) {
        this.neighbors.add(e);
    }

    public int getId() {
        return id;
    }

    public List getNeighbors() {
        return neighbors;
    }

    @Override
    public String toString() {
        return "Node{" +
                "id=" + id +
                ", neighbors=" + neighbors +
                "}"+ "\n";
    }
}

这个类也很简单-只是一个构造函数和一个相邻节点的列表。

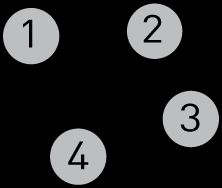
在我们的两个类中，我们都实例化一个图形并用几个节点填充它：

public class GraphInit {
    public static void main(String[] args) {
        Graph g = new Graph();
        Node node1 = new Node(1);
        Node node2 = new Node(2);
        Node node3 = new Node(3);
        Node node4 = new Node(4);
        node1.addNeighbor(2);
        node2.addNeighbor(3);
        node4.addNeighbor(3);
        g.addNode(node1);
        g.addNode(node2);
        g.addNode(node3);
        g.addNode(node4);
        System.out.println(g);
    }
}

输出：

 

 

 

Graph{nodes=[Node{id=1, neighbors=[2]}
, Node{id=2, neighbors=[3]}
, Node{id=3, neighbors=[]}
, Node{id=4, neighbors=[3]}
]}

现在让我们实现算法本身：

private static void topoSort(Graph g) {

    // Fetching the number of nodes in the graph
    int V = g.getSize();

    // List where we'll be storing the topological order
    List order = new ArrayList<> ();

    // Map which indicates if a node is visited (has been processed by the algorithm)
    Map visited = new HashMap<>();
    for (Node tmp: g.getNodes())
        visited.put(tmp.getId(), false);

    // We go through the nodes using black magic
    for (Node tmp: g.getNodes()) {
        if (!visited.get(tmp.getId()))
            blackMagic(g, tmp.getId(), visited, order);
    }

    // We reverse the order we constructed to get the
    // proper toposorting
    Collections.reverse(order);
    System.out.println(order);
}

private static void blackMagic(Graph g, int v, Map visited, List order) {
    // Mark the current node as visited
    visited.replace(v, true);
    Integer i;

    // We reuse the algorithm on all adjacent nodes to the current node
    for (Integer neighborId: g.getNode(v).getNeighbors()) {
        if (!visited.get(neighborId))
            blackMagic(g, neighborId, visited, order);
    }

    // Put the current node in the array
    order.add(v);
}

如果调用topoSort(g)上面初始化的图，则会得到以下输出：

[4, 1, 2, 3]

完全正确。

使用拓扑排序进行问题建模

在现实世界中，可以使用拓扑排序为Lego玩具，汽车和建筑物编写正确的组装说明。

实际上，大多数开发人员每天（或每小时）使用一种拓扑排序，尽管它是隐式的。如果您在考虑Makefile或仅是Program依赖项，那将是完全正确的。

典型的Makefile如下所示：

area_51_invasion.out: me.c, the_boys.c, Chads.c, Karen.c, the_manager.c
    #instructions for assembly when one of the files in the dependency list is modified

通过这一行，我们定义了哪些文件依赖于其他文件，或者更确切地说，我们正在定义应按照哪种拓扑顺序检查文件，以查看是否需要重建。

也就是说，如果area_51_invasion.out依赖the_boys.c并且the_boys.c由于某种原因进行了修改，那么我们需要重建area_51_invasion.out，并且依赖于同一文件的所有内容，即按照Makefile拓扑顺序排列的所有内容。

结论

基本上，我们经常考虑考虑Toposort。您甚至可能已经在软件中实现了它，甚至都不知道。如果您还没有，我强烈建议您试试看！