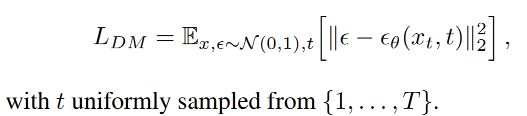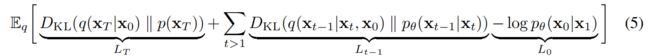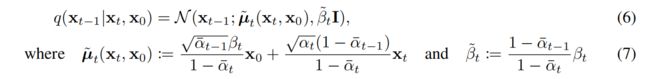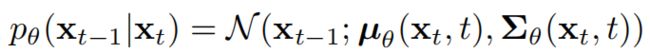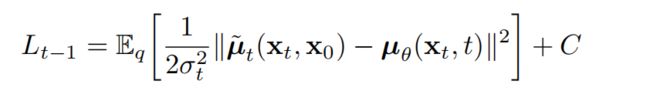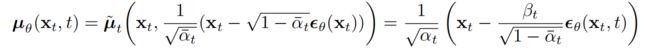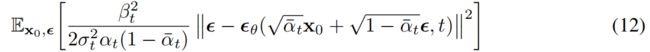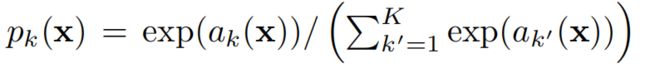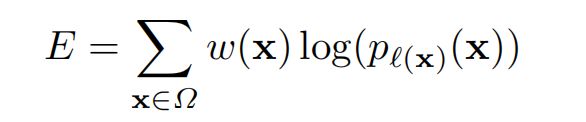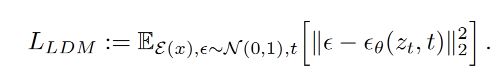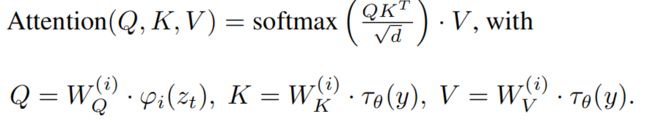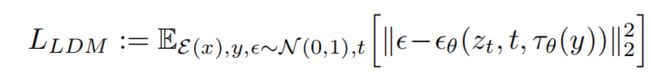AI绘画Stable Diffusion原理之扩散模型DDPM
前言
传送门:
stable diffusion:Git|论文
stable-diffusion-webui:Git
Google Colab Notebook部署stable-diffusion-webui:Git
kaggle Notebook部署stable-diffusion-webui:Git
AI绘画,输入一段文本就能生成相关的图像,stable diffusion便是其中一个重要分支。自己对其中的原理比较感兴趣,因此开启这个系列的文章来对stable diffusion的原理进行学习(主要是针对“文生图”[text to image])。
上述的stable-diffusion-webui是AUTOMATIC1111开发的一套UI操作界面,可以在自己的主机上搭建,无限生成图像(实测2080ti完全能够胜任),如果没有资源,可以白嫖Google Colab或者kaggle的GPU算力,其部署教程在上面传送门。
其中stable diffusion的基础模型可以hugging face下载,而C站可以下载各种风格的模型。stable diffusion有一个很大的优势就是基于C站中各式各样的模型,我们可以进行不同风格的AI绘画。
上一篇文章,对stable diffusion其中的一个组件进行学习:Autoencoder/VQGANs,可以将图像从像素空间压缩到低维的隐空间。而这篇文章会对剩余的知识进行阐述,包括:CLIP、扩散模型DDPM、UNet模型。
原理简介
Stable Diffusion is a latent text-to-image diffusion model。stable diffusion本质是一种latent diffusion models(LDMs),隐向量扩散模型。diffusion models (DMs)将图像的形成过程分解为去噪自动编码器(denoising autoencoders)的一系列操作,但这些都是直接在像素空间上进行的操作,因此对于昂贵的计算资源,特别是高像素的图像。而LDMs则是引入隐向量空间,能够生成超高像素的图像。
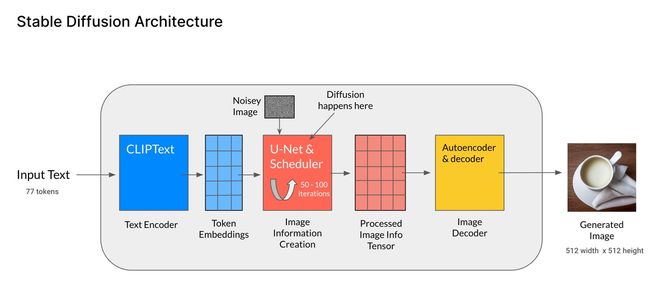
这里,我们先整体地来了解下stable diffusion的结构组成,后面再对每个组件进行拆开逐一理解。整体结构如下图[Stable Diffusion Architecture]:
- 文本编码器:人类输入的文本即prompt,经过CLIP模型中的Text Encoder,转化为语义向量(Token Embeddings);
- 图像生成器(Image information Creator):由U-Net和采样器组成,输入输出都是低维向量即在隐向量空间。由随机生成的纯噪声向量(即下图中的Noisey Image)开始,文本语义向量作为控制条件进行指导,由U-Net和采样器不断迭代生成新的越具有丰富语义信息的隐向量,这就是扩散过程diffusion;
- 图像解码器(Image Decoder)- Autoencoder:迭代了一定次数之后,得到了包含丰富语义信息的隐向量(Processed Image Info Tensor),低维的隐向量经过Autoencoder解码到原始像素;
- 第2步就是LDMs和DMs的区别,LDMs是在latent space进行扩散,而DMs则是在pixel space,这也是性能提升的关键。
CLIP
论文:Learning Transferable Visual Models From Natural Language Supervision
Git:openai/CLIP
因为这篇文章的主题不是CLIP,在这里就简单介绍下CLIP模型。CLIP也是出自OpenAI,其思想是利用**对比学习,拉近配对的图片和文本(image-text pairs)的表征向量的距离,而让不配对的距离尽量远。**这是许多多模态预训练会使用到的方法,NLP领域也会看到,如SimCSE。其实也很像推荐系统中的召回阶段。
- image-text pairs:即一张图片,并包含描述这种图片的文本内容;
- Text Encoder:可以是简单的CBOW模型,也可以是Transform结构的BERT,得到输入文本的表征向量;
- Image Encoder:可以是ResNet或者Vision Transformer(ViT),得到图片的表征向量;
- projection:然后对文本和图像的表征向量投射到同一空间向量,即projection,并进行L2 normalization;
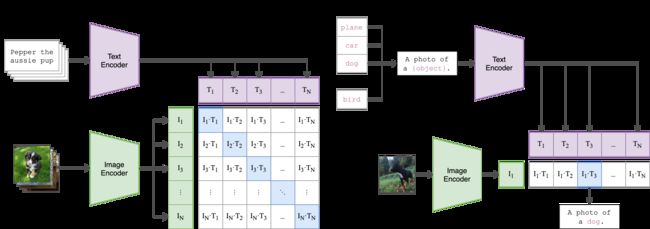
- 对比学习训练:输入是n个image-text pairs,在一个batch内,使用cross_entropy_loss,让同一对的文本和图像向量的内积尽量大(cosine相似度尽量高),让图像向量与batch内的其它文本向量的内积尽量小(cosine相似度尽量低),如下图[CLIP](1);
- 表征向量:经过充分预训练的CLIP模型,可以为输入图像和文本输出具有丰富语义信息的表征向量,作为多种特定任务的输入,比如图像和文本的相似度预测。
- 零样本推理:甚至可以做zero-shot的分类任务,比如下图[CLIP](2-3),给一张狗的图片,再构造包含所有标签的文本(A photo of a [label]),那么狗的图片向量与文本-A photo of a dog的向量相似度更高,比起其他标签文本如A photo of a cat的向量。
DMs&DDPM
[1] DMs起源论文:Deep Unsupervised Learning using Nonequilibrium Thermodynamics
[2] DDPM论文:Denoising Diffusion Probabilistic Models
Diffusion Models [ 1 ] ^{[1]} [1]. 论文认为DMs是通过逐步去噪的正态分布变量去学习拟合一种数据分布的概率模型,相当于学习固定长度为T的马尔可夫链的反转过程。
对于图像合成来说,正如开头提到的,其过程其实是为去噪自动编码器(denoising autoencoders)的一系列操作即对应序列 ϵ θ = ( x t , t ) ; t = ( 1 … T ) \epsilon_{\theta}=(x_t,t);t=(1\dots T) ϵθ=(xt,t);t=(1…T),包括训练阶段的前向(扩散)过程以及推理阶段的反向过程,但这其实都是基于扩散模型DDPM [ 2 ] ^{[2]} [2](2020年提出)来完成的,不过其数学框架 [ 1 ] ^{[1]} [1]其实在2015年就有了。
训练
ϵ θ = ( x t , t ) ; t = ( 1 … T ) \epsilon_{\theta}=(x_t,t);t=(1\dots T) ϵθ=(xt,t);t=(1…T) 这个序列就是DDPM每一步的输出,DDPM的训练目标是去预测序列中的每一步的模型输入 x t x_t xt的去噪版本,直白来说,其实就是去拟合加入的噪声,而 x t x_t xt则是对原始图像 x + x+ x+噪声,目标可以简化如下式:
其中backbone ϵ θ ( ∘ , t ) \epsilon_{\theta}(\circ,t) ϵθ(∘,t)使用的是UNet模型。
整个训练步骤如下:
- 第t步时,对原始图像 x x x加入一定比重的标准高斯分布的噪声 ϵ \epsilon ϵ得到 x t x_t xt
- x t x_t xt作为模型的输入,经过UNet模型得到预测的噪声 ϵ θ ( x t , t ) \epsilon_{\theta}(x_t,t) ϵθ(xt,t)
- 训练的目标则是让预测的噪声与真实的噪声尽可能的接近,相似度度量使用KL散度
- 循环上述步骤 t ∼ u n i f o r m ( { 1 , . . . , T } ) t \sim uniform(\{1,...,T\}) t∼uniform({1,...,T})
其中, 0 ≤ β t ≤ 1 0\le \beta_t \le 1 0≤βt≤1,并且是随着步数t逐渐增长的。由于 α ˉ t \bar{\alpha}_t αˉt是累乘的,那么噪声的权重则会越来越大,即图像+噪声会越来越模糊,而生成阶段(推理)则是反转的过程,由纯噪声开始,生成的图像越来越清晰。
采样生成
采样阶段与训练是反着来的,由随机噪声 x t x_t xt开始,逐渐褪去噪声 ϵ θ ( x t , t ) \epsilon_{\theta}(x_t,t) ϵθ(xt,t),相当于为加噪的图片去噪,生成比上一步更为清晰的图像,即 x t → x t − 1 → . . . → x 0 x_t \rightarrow x_{t-1} \rightarrow ... \rightarrow x_0 xt→xt−1→...→x0即 p ( x t − 1 ∣ x t ) p(x_{t-1}|x_t) p(xt−1∣xt),整体的采样生成算法如下:
理论推导
上述大致讲述了扩散模型的训练及采样生成的流程步骤,这一节则是数学公式的理论推导,不感兴趣的可以跳过。
1. 生成模型 p θ ( x 0 ) p_{\theta}(x_0) pθ(x0)
DDPM的目标是为了得到一个图像生成模型,即上述所说由随机噪声 x T x_T xT开始,逐步生成比上一步更为清晰的图像 x t → x t − 1 → . . . → x 0 x_t \rightarrow x_{t-1} \rightarrow ... \rightarrow x_0 xt→xt−1→...→x0,论文叫作reverse process,是一个以 p ( x T ) = N ( x T ; 0 , I ) p(x_T)=N(x_T;0,I) p(xT)=N(xT;0,I)为起点和有着充分学习的高斯转移的马尔可夫链,如下式: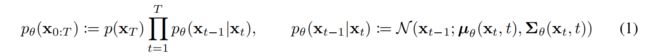
2. 扩散模型 q q q
为了得到生成模型 p θ ( x 0 : T ) p_{\theta}(x_{0:T}) pθ(x0:T),需要去学习拟合一个扩散模型 q ( x 1 : T ∣ x 0 ) q(x_{1:T}|x_0) q(x1:T∣x0),称为forward process or diffusion process,是一个给真实样本 x 0 x_0 x0逐步增加高斯噪声的马尔可夫链,噪声强度schedule为 β 1 , . . . , β T \beta_1,...,\beta_T β1,...,βT,如下式: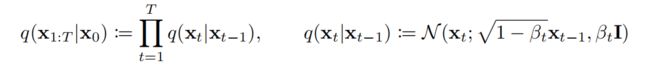
让 α t : = 1 − β t a n d α ˉ t : = ∏ s = 1 t α s a n d ε ∼ N ( 0 , I ) \alpha_t:=1-\beta_t\ and\ \bar{\alpha}_t:=\prod^t_{s=1}\alpha_s\ and\ \varepsilon\sim N(0,I) αt:=1−βt and αˉt:=∏s=1tαs and ε∼N(0,I),则可以得到:
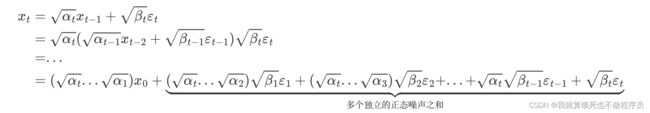
那么根据概率论的知识——正态分布的叠加性,即上述多个独立的正态噪声之和的分布,实际上是均值为 0、方差为 ( α t . . . α 2 ) β 1 + ( α t . . . α 3 ) β 2 + . . . + α t β t − 1 + β t (\alpha_t...\alpha_2)\beta_1+(\alpha_t...\alpha_3)\beta_2+...+\alpha_t\beta_{t-1}+\beta_t (αt...α2)β1+(αt...α3)β2+...+αtβt−1+βt的正态分布;
接着因为 α t = 1 − β t \alpha_t=1-\beta_t αt=1−βt,我们可以得到上式的各项系数平方和为1,即:(将 β t \beta_t βt用 1 − α t 1-\alpha_t 1−αt代入展开即可算出)
( α t . . . α 1 ) + ( α t . . . α 2 ) β 1 + ( α t . . . α 3 ) β 2 + . . . + α t β t − 1 + β t = 1 (\alpha_t...\alpha_1)+(\alpha_t...\alpha_2)\beta_1+(\alpha_t...\alpha_3)\beta_2+...+\alpha_t\beta_{t-1}+\beta_t=1 (αt...α1)+(αt...α2)β1+(αt...α3)β2+...+αtβt−1+βt=1
到这里,就推导出论文直接摔出来的转换公式了,即下式4:
3. 优化目标
正如前面说到,需要利用扩散模型(forward process)来拟合生成模型(reverse process),因此扩散模型的优化目标L是让reverse process的分布与forward process的分布尽可能一致,用negative log likelihood表达如下式: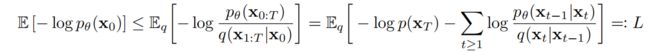
然后根据下面的公式推导,我们可以将negative log likelihood的优化目标L转化为KL散度的形式 [ 1 ] ^{[1]} [1](其中由于前向过程q是马尔可夫链,可以引入 x 0 x_0 x0;接着使用贝叶斯公式,从而转化为 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0)的形式):
KL散度的形式的L如下式5(KL散度表示的两个概率分布的差异):
这个KL散度衡量了 p θ ( x t − 1 ∣ x t ) p_{\theta}(x_{t-1}|x_t) pθ(xt−1∣xt)和forward process posteriors q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0)(前向过程的后验),而forward process posteriors是可以由 x 0 x_0 x0来表示的,如下式:
上式7的推导需要通过将 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0)进行贝叶斯公式转换,然后式子中的概率分布 q q q用正态分布的公式即自然常熟e的指数形式表示去计算化简。
4. Forward process and L T L_T LT
因为forward process中的 β t \beta_t βt是通过重参数得到,或者直接固定为一个常量,所以q是没有学习参数的,那就意味着 L T L_T LT在训练时是一个可以忽略的常量。
5. Reverse process and L 1 : T − 1 L_{1:T-1} L1:T−1
再来讨论 p θ ( x t − 1 ∣ x t ) p_{\theta}(x_{t-1}|x_t) pθ(xt−1∣xt),首先,让 ∑ θ ( x t , t ) = σ t 2 I \sum_{\theta}(x_t,t)=\sigma^2_tI ∑θ(xt,t)=σt2I,依赖时间t的常量。论文通过实验, σ t 2 = β t \sigma^2_t=\beta_t σt2=βt和 σ t 2 = β ~ t = 1 − α ˉ t − 1 1 − α ˉ t β t \sigma^2_t=\tilde{\beta}_t=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\beta_t σt2=β~t=1−αˉt1−αˉt−1βt得到的结果是差不多的。
接着,因此 p θ ( x t − 1 ∣ x t ) p_{\theta}(x_{t-1}|x_t) pθ(xt−1∣xt)最重要的是能够得到 μ θ ( x t , t ) \mu_{\theta}(x_t,t) μθ(xt,t)的表征(仅剩未知的),上式5 L t − 1 L_{t-1} Lt−1中两个正态分布的KL散度可以表达为等式8:
其中,C是一个与参数 θ \theta θ无关的常量,因此, μ θ \mu_{\theta} μθ其实是一个去预测forward process posteriors均值 μ ~ t \tilde{\mu}_t μ~t的模型。再将等式8展开,并且代入等式4和等式7,可以得到:
等式10表示模型 μ θ \mu_{\theta} μθ需要通过给定的 x t x_t xt去预测下式这部分:
x t x_t xt其实就是模型的输入,因此加入参数化,最终 μ θ \mu_{\theta} μθ的预测如下:
其中, ϵ θ ( ∘ , t ) \epsilon_{\theta}(\circ,t) ϵθ(∘,t)上面也提到,是一个通过 x t x_t xt去预测噪声 ε \varepsilon ε的backbone比如U-Net模型。
到这里,整个**生成模型 p θ ( x t − 1 ∣ x t ) p_{\theta}(x_{t-1}|x_t) pθ(xt−1∣xt)**就推导出来了,正如等式1,包括含有学习参数的均值部分 μ θ ( x t , t ) \mu_{\theta}(x_t,t) μθ(xt,t)和不含学习参数的方差部分 σ t 2 I \sigma^2_tI σt2I,整个采样过程如下图:
再根据等式4将 x t x_t xt代入等式10,那么等式10 L t − 1 L_{t-1} Lt−1则等于下式:
接着,论文将系数简化即reweighting,发现能够获取更好的效果,这有利于让模型关注更为困难的去噪任务:
扩散模型的训练优化目标loss也推导结束,整个训练算法如下图:
UNet
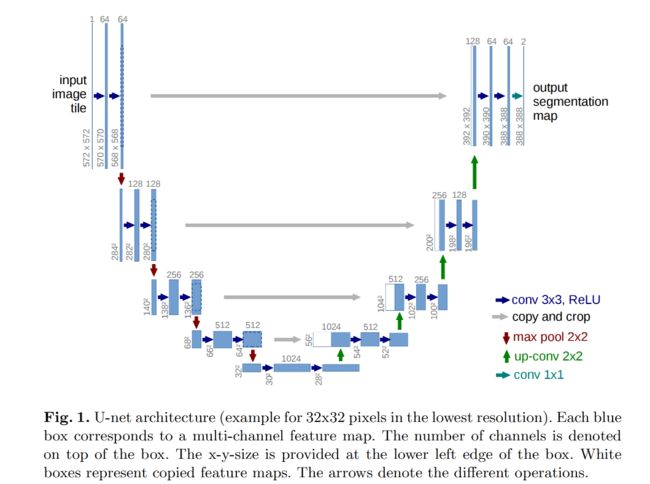
论文:U-Net: Convolutional Networks for Biomedical Image Segmentation
从上图UNet的结构可以看出,它其实跟AutoEncoder结构有些相似,从高维的输入,压缩(contracting path)到低维的中间层,然后再扩展(expansive path)到高维的输出:
- 但AutoEncoder很多是为了降维,其输出是要去拟合输入的;
- 而UNet模型的输入则是图像,输出是为了去拟合标签,比如上述的扩散模型是去拟合噪声,而UNet的论文则是为了去拟合分割图segmentation maps;
- UNet的contracting path和expansive path使用的卷积网络
- UNet最后输出的feature channel数量是根据标签类别数决定的,即每个class都有自己的一个feature channel
论文在2015年发表,当时卷积网络主要用于分类任务,其输出是一张图片的标签,而生物学图像任务中,往往更需要具有局部性localization,比如一个类别的标签应该是分配给一块局部区域的每个像素点的。
像素点x对于第k个标签类别的预测概率如下:
其中,K是标签所有类别的数量。
UNet的损失函数使用cross entropy,即每个像素点的真实标签类别 ℓ \ell ℓ的预测概率交叉熵:
w则是为了控制某些像素点的重要性。
LDMs
在上一篇文章中介绍了视觉压缩模型AutoEncoder/VQGANs,包括能够将图片从像素空间映射到隐向量空间的编码器 ε \varepsilon ε以及隐向量空间重建回像素空间的解码器 D D D。因此,LDMs能够从聚焦于数据中重要的语义信息bits,以更低的维度实现更高的计算效率:
而 z t z_t zt便是编码器 ϵ t \epsilon_t ϵt输出的隐向量空间。最终在隐空间的(反向)扩散过程输出 p ( z ) p(z) p(z)则能够通过解码器 D D D解码到图像(像素)空间。
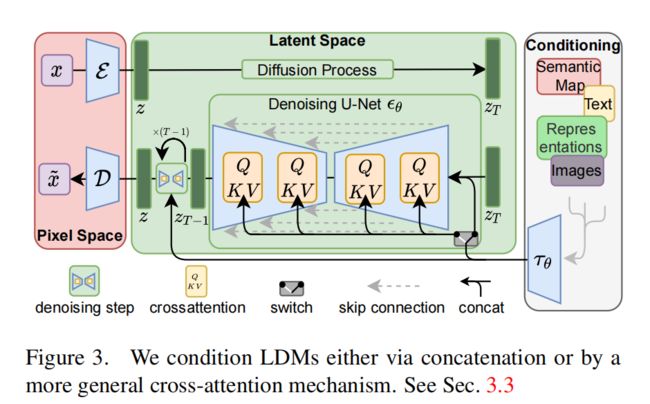
使用隐空间的LDMs版本原理基本相同,只是多了能够在像素空间与隐空间之间相互映射的编码器和解码器,如下图:
调节机制
跟其他类型的生成模型类似,扩散模型是有能力去建模条件分布 p ( z ∣ y ) p(z|y) p(z∣y)的,这可以在denoising autoencoder中的 ϵ θ \epsilon_{\theta} ϵθ引入这个控制条件y即conditional denoising autoencoder ϵ θ ( z t , t , y ) \epsilon_{\theta(z_t,t,y)} ϵθ(zt,t,y),来调节合成过程,这个y就可以是本文讲的"文生图"中的文本prompt。论文在UNet引入cross-attention layer来实现这个过程,如下图:
- 首先,需要有一个y领域的Encoder,能够将y映射到一个表征向量 τ θ ( y ) ∈ R M × d τ \tau_{\theta(y)}\in \mathbb{R}^{M \times d_{\tau}} τθ(y)∈RM×dτ,比如BERT,能够将文本映射为向量;
- φ i ( z t ) ∈ R N × d ϵ i \varphi_i(z_t)\in \mathbb{R}^{N \times d^i_{\epsilon}} φi(zt)∈RN×dϵi 表示UNet模型 ϵ θ \epsilon_{\theta} ϵθ的输出,一个中间表征;
- 引入控制条件y之后, φ i ( z t ) \varphi_i(z_t) φi(zt)会和 τ θ ( y ) \tau_{\theta(y)} τθ(y)经过cross-attention layer,注意力机制仍然是常规的做法:
那么,LDMs的loss则变成下式:
总结
- CLIP通过对比学习训练,得到一个文本编码器和图像编码器,可以让配对的文本表征向量和图像表征向量距离更近,其主要为stable diffusion提供了文本编码的能力;
- DMs在训练阶段逐步为干净的图片加入高斯噪声,并去拟合这个噪声,而在采样生成(推理)阶段则是由随机的噪声开始,逐步预测噪声然后去去噪,直至得到高质量的图片,而这主要是通过DDPM来实现;
- LDMs则是在DMs的基础上引入了Autoencoder能够将图像从像素空间压缩到隐空间,极大提升计算效率;
- 并且LDMs还具有引入文本控制条件的建模能力,通过UNet与文本表征进行注意力交叉,实现文生图的能力。