算法与设计分析--分治算法的设计与分析
某不知名学校的第二次算法实验报告,一共四道题 全部来自力扣
第一题
169. 多数元素
题目描述:
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入: [3,2,3]
输出: 3
示例 2:
输入: [2,2,1,1,1,2,2]
输出: 2
这道题的话我的思路一开始是想到哈希,记录每个数据出现次数 最多的那个就是答案,但是发现数据到了1e5 ,而且下面的题目思考提醒可以用时间复杂度O(n) 空间复杂度O(1)的算法,那么额外开辟空间去整哈希表肯定是不行的了,只能原地操作
排序的算法时间复杂度是O(logn) 接近O(n)的水平, 而且也是原地操作,最重要是思路简单
把所有数排序,中间那个数字不是就一定出现次数大于n/2了吗
代码如下:
class Solution {
public:
int majorityElement(vector& nums) {
sort(nums.begin(), nums.end());
int k = nums.size();
return nums[ k / 2 ];
}
}; 很简单是吧,排序函数就不自己写了,这道题考的也不是排序
第二题
53. 最大子数组和
题目描述:
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
首先这道题很容易想到滑动窗口,但是突然发现,这个题他的窗口大小是会变化的,而且并不是一个队列结构,那我们只能另辟蹊径,我们发现,最大子序列他的第一个和最后一个元素一定是正数
我们依次往后累加,同时保留最大序列,如果发现整个序列为负时,则需要更新整个序列
sum = num完整代码+注释如下:
class Solution {
public:
int maxSubArray(vector& nums) {
int res = nums[0]; // 保存答案序列
int sum = 0;
for(int num : nums)
{
if(sum > 0 )
sum += num; //依次累加
else
sum = num; // 序列为负数 更新起点
res = max(res, sum); // 每次取最大序列
}
return res;
}
}; 第三题
215. 数组中的第K个最大元素
题目描述:
在未排序的数组中找到第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
说明:
你可以假设 k 总是有效的,且 1 ≤ k ≤ 数组的长度
思路:这道题就是快排的思路,本质上还是个快排,而且题目建议最好是用接近O(n)的时间复杂度,那很明显就是用快排思路做,但是很多语言都有排序函数,比如c++的库函数sort,会在元素少的时候有归并排序,元素多的时候用快速排序,时间复杂度接近O(n)
先放一个库函数的代码:
class Solution {
public:
int findKthLargest(vector& nums, int k) {
int l = nums.size();
sort(nums.begin(), nums.end());
return nums[l - k];
}
}; 很简单对吧 但是这道题毕竟要考的是快排,把题目的本质用库函数实现了,实在不推荐
正常写法(求第K个数):
#include
using namespace std;
const int N = 100010;
int q[N];
int quick_sort(int q[], int l, int r, int k)
{
if (l >= r) return q[l];
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while (i < j)
{
do i ++ ; while (q[i] < x);
do j -- ; while (q[j] > x);
if (i < j) swap(q[i], q[j]);
}
if (j - l + 1 >= k) return quick_sort(q, l, j, k);
else return quick_sort(q, j + 1, r, k - (j - l + 1));
}
int main()
{
int n, k;
scanf("%d%d", &n, &k);
for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);
cout << quick_sort(q, 0, n - 1, k) << endl;
return 0;
} 第四题
932. 漂亮数组
题目描述:
如果长度为
n的数组nums满足下述条件,则认为该数组是一个 漂亮数组 :
nums是由范围[1, n]的整数组成的一个排列。- 对于每个
0 <= i < j < n,均不存在下标k(i < k < j)使得2 * nums[k] == nums[i] + nums[j]。给你整数
n,返回长度为n的任一 漂亮数组 。本题保证对于给定的n至少存在一个有效答案。示例 1 :
输入:n = 4 输出:[2,1,4,3]示例 2 :
输入:n = 5 输出:[3,1,2,5,4]提示:
1 <= n <= 1000
先分析信息:
1.这是一段连续的序列
2.下标的大小i < k < j
3.条件是要不成立 而左边是2*nums[k] 左边是偶数 且只需要其中一个有效答案
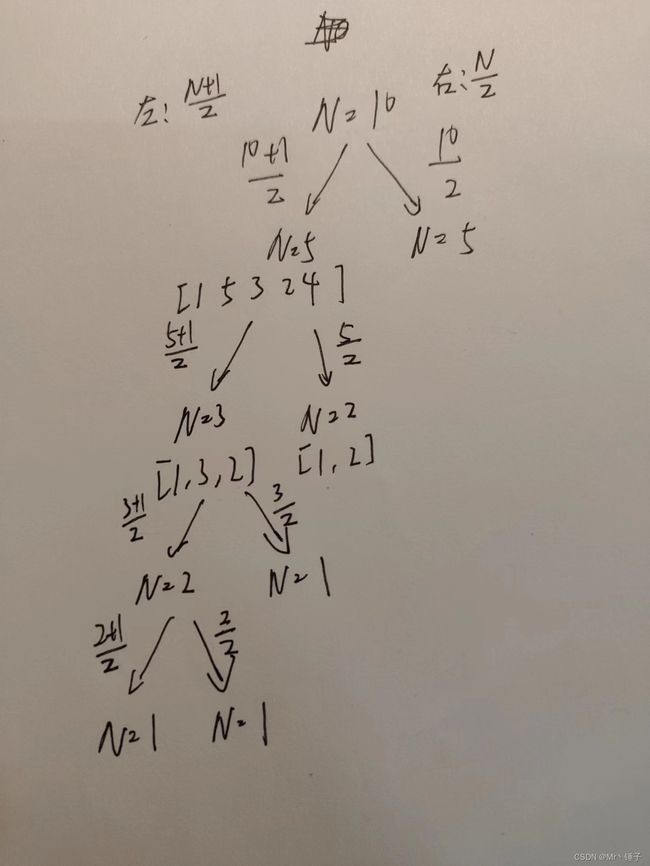
先顺着分治的思想观察一下(废话,这次实验不就是分治吗) 把数组从中间切开 左边和右边满足什么规律?
好的,看样例好像确实看不出什么,大概率是道搞数学的
发现他答案不止一组,n=4时候 [1,3,2,4]可行
n = 5 [1,5,3,2,4]可行
加上题目给的*2条件 我们可以推出 偶数 != 奇数 + 偶数 两边不会相等
我们设 x = nums[i] y = nums[k] z = nums[j]
对于一个正整数 N ,我们寻找中点将其等分成两部分 ,left 和 right ,如果 left 和 right 都是漂亮数组,同时 left 部分全部是奇数 , right 部分全部是偶数 ,那么left + right 组成的数组一定也是漂亮数组 。
同时可以发现
如果x, y, z 是漂亮数组,则 k * x + b, k * y + b, k * z + b 一定也是漂亮数组;
那么就可以往下分了左端 (n + 1) /2 分奇数 右端 n / 2 分偶数
代码+注释如下:
class Solution {
public:
vector beautifulArray(int n) {
vector ans, left, right;
left = beautifulArray((n+1)/2);
right = beautifulArray(n/2);
for(int l : left){
ans.push_back(l * 2 - 1); //回溯
}
for(int r : right){
ans.push_back(r * 2); //回溯
}
//这里代码先push左端后右端 所以ans左边全是奇数 右边全是偶数 但是符合题目要求
else ans.push_back(1);
return ans;
}
};
当然 看完别人题解后 发现动态规划也能写,原理一样 ,只是思维量更大一点
代码如下:
class Solution {
public:
unordered_map> mp;
vector beautifulArray(int n) {
vector> dp(n+1);
// 初始化
dp[1].push_back(1);
// 状态转移
for(int i=2; i<=n; ++i){
for(int l : dp[(i+1)/2]){
dp[i].push_back(l * 2 - 1);
}
for(int r : dp[i/2]){
dp[i].push_back(r * 2);
}
}
return dp[n];
}
};
前面几题都是来划水的,最后一题确实是巧妙 主要是分治思想没有体会精髓,平时哪怕用了也不会想到,平时就算要解题也不会第一时间想到分治