四万高手过招，这份阿里全球数学竞赛试题你真的不要看吗 ...

雷锋网 AI 科技评论按，今年下半年，阿里巴巴举办了一场全球数学竞赛，在短短 6 天的报名时间中，有 4 万多名来自国内外的选手报名了这次竞赛，其中海外选手占了三分之一，并且有 77% 的参赛者是学生，超过一半的学生选手是硕士在读或者硕士以上学历，高中生比例也占据 8%。

来自于 11 个国家和地区的选手参加了比赛，而年龄最小的仅 13 岁，年纪最大的年近五旬。最终，有 328 位选手通过了预选赛，进入决赛。其中有很多在国际数学竞赛中取得优异成绩的「大神」。

经过激烈角逐，共有 51 名选手在决赛中脱颖而出，下面是阿里巴巴官方公布的决赛获奖名单：

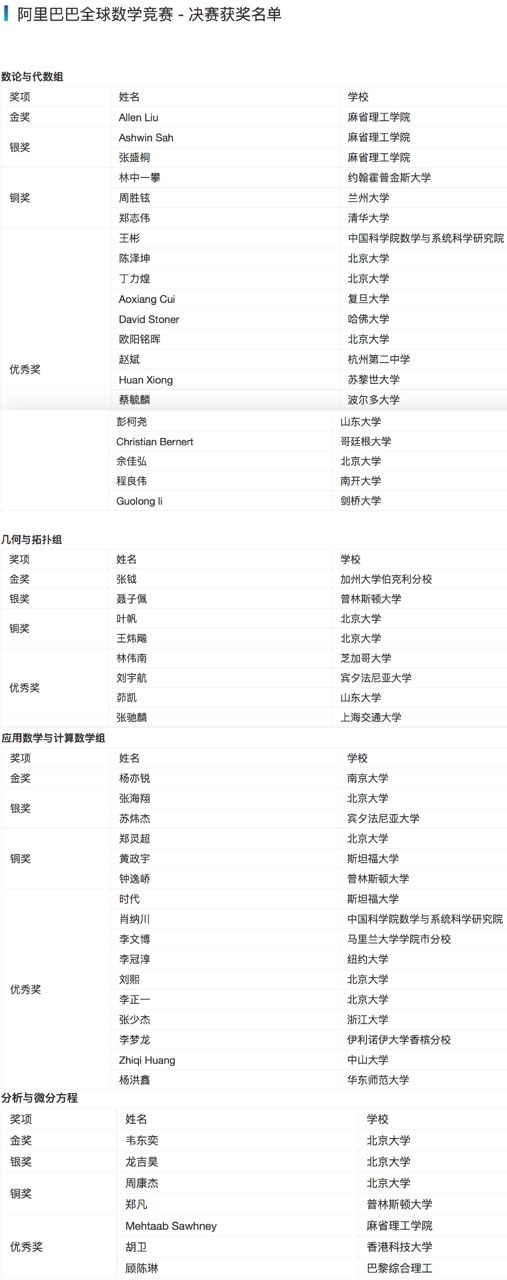
官网获奖名单图

金奖获得者 4 人：Allen Liu，张钺，杨亦锐，韦东奕

银奖获得者 6 人：Ashwin Sah、张盛桐、聂子佩、张海翔、苏炜杰、龙吉昊

铜奖获得者 10 人：林中一攀、周胜铉、郑志伟、叶帆、王炜飚、郑灵超、黄政宇、钟逸峤、周康杰、郑凡

优秀奖获得者 31 人：王彬、陈泽坤、丁力煌、Aoxiang Cui、David Stoner、欧阳铭晖、赵斌、Huan Xiong、蔡毓麟、彭柯尧、Christian Bernert、余佳弘、程良伟、Guolong li、林伟南、刘宇航、茆凯、张驰麟、时代、肖纳川、李文博、李冠淳、刘熙、李正一、张少杰、李梦龙、Zhiqi Huang、杨洪鑫、Mehtaab Sawhney、胡卫、顾陈琳；

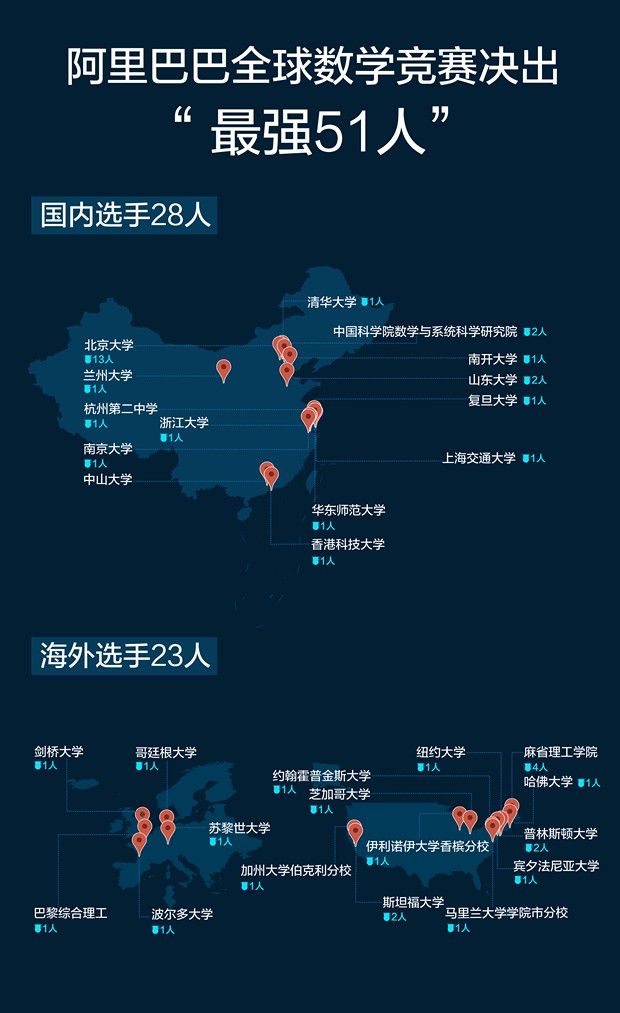
全球「最强 51 人」分布图

可以看到，从全球4万多名参赛者中脱颖而出的「最强 51 人」来自 20 多所全球一流大学，国内选手 28 人，海外选手 23 人。其中北京大学贡献了 13 位获奖选手，是获奖人数最多的高校，麻省理工学院次之，贡献 4 名获奖选手。获奖者中年龄最小的获奖者仅有 18 岁。

这 51 人均将获得由多位国际著名数学家领衔授课的数学大师班门票。同时，获得金银铜奖的 20 名选手将会共同分享总额 100 万元的奖学金。

据悉，本次数学大赛组委会在决赛举办前一个月就单独成立命题小组，其中包括应用数学领域最高成就——高斯奖获得者 Stanley Osher。决赛出题者之一北京大学数学系教授董彬表示，决赛题目水平相当于美国 top 20 高校博士入学考试的水平，需要综合运用高年级本科及低年级研究生课程的数学知识。在赛题选择上，大赛更关注选手们对实际数学知识应用的考察，而非过去竞赛所偏重的数学技巧。预选赛和决赛都是线上答题，题目都是英文，解答既可以用中文也可以用英文。其中，预选赛的题目比较贴近个人生活，决赛更注重对数学基础知识的考察。

目前决赛的试题解析还没有公布，雷锋网整理了预选赛试题和答案，让我们来看看吧~

预选赛具体形式是应用题&建模题&数学基础题，共三题，每题三问，需要提供解题步骤。第一题 30 分，第二题 40 分，第三题 30 分，全部正确解决问题得满分。组委会会选择前 300 名进入决赛。

第一题

在下面的所有小题中，不考虑退货

A.「双十一」期间，一家电商店铺 A 有满 60 返 5 块的优惠券，可叠加使用（比如，买 120 块的东西，用两张优惠券，只需付 120-5*2=110 块）。此外，电商平台全场提供满 299 减 60 的优惠券（可凑单），每单限用一张，可与店铺的优惠券叠加使用（比如，原价 299 块的一单，最终价格是 299-5*4-60=219）。原价不满 29 则不能减去全场折扣 60，不足 299 时，用户可以在别家商店凑单。

请问：小明打算在这家店铺买一款 250 块的耳机和 600 块的音箱，怎么买最划算？

B. 现在您开了一家电商店铺，卖与 A 店同款的耳机和音箱，标价相同，您计划提供满 99 返 x 的优惠券，x 为大于 0，小于 99 的整数，与 A 店不同的是，您的优惠券每单限用一张（比如，买 250 块需付 250-x 块，而不是 250-2x 块）。双 11 期间，电商平台全场满 299 减 60 依然适用。

请问：x 至少等于多少时，小明在您的店铺买耳机和音箱其中一种会更便宜（至少 1 元）？又请问：x 至少等于多少时，小明在您的店铺既买耳机又买音箱总和会更便宜（至少 1 元）？

C. 建模题。对比单卖和捆绑销售下的利润期望。假设耳机（产品 1）和音箱（产品 2）的单件销售的单位成本分别是 c1 和 c2（包含生产、存储、运输、促销等所有成本）。一个访问店铺的客户对两件产品的心理价值分别是均匀分布在 [0，u1]，[0，u2] 的区间上随机变量 S1 和 S2。假设 S1 和 S2 相互独立。本题有三小问。

如何分别设定产品价格 p1 和 p2，以最大化每个到访客户带来的利润期望。这里假设 c1

现在假设产品 1 和 2 捆绑销售，成本是 c12=t（c1+c2）。因为节省了包装和运输成本，假设 0

单卖和捆绑销售，哪个利润更优，还是不一定？为什么？

第二题

a. 附图中有一个无向图，其中圈内数字代表一个地点，边 e 上的数字代表长度 Le（双向相同）。一位外卖小哥在起点 A，要去 3 个商家（B1，B2，B3）取餐，送到 3 个对应的地方（C1，C2，C3），即 B1 至 C1，B2 至 C2，B3 至 C3。小哥的电动动力车的箱子同时最多装下 2 份外卖。

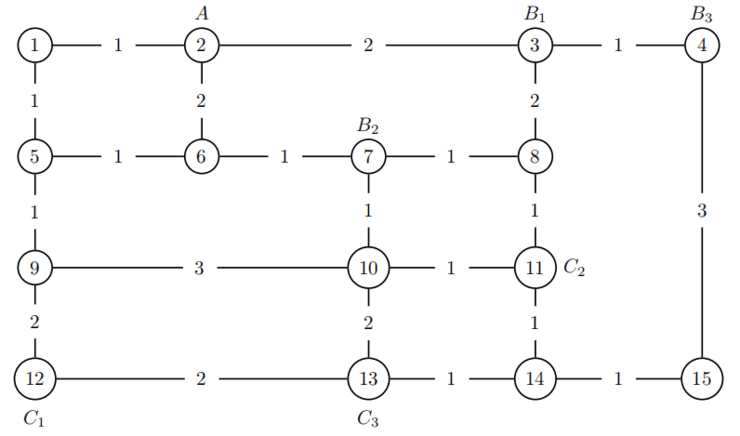
请问：小哥该怎么走最短路径？这个最短路径的长度是多少，这里 A 是出发点，最后一餐（不限次序）送达地为终点。为了简化问题，假设商家已经准备好了外卖，小哥取餐送餐不用等。又假设每份外卖重量大小一样。

b. 此题与上图无关，而是考虑一个一般的图，图中有很多点和边。外卖小哥刚刚取了一份外卖，计划通过图上的边 e1、e2...em 送给目的地，途中经过每条边 e 的时候，以概率 Pe[0,1] 会收到送至相同地点的另一单外卖。（一条边上收到另两单及以上的概率小，暂忽略不计）。假设对应边 e1、e2...em 的概率为 P1、P2...Pm。

请问：送一次外卖，小哥平均能收到几个送去相同地址的新单（不考虑电动车的箱子容量）？小哥收到至少一个区相同地址的新单的概率是多少？

c. 此题延续上题，但不再固定路径，而是对路线进行优化。假设小哥每送一单外卖有固定收益 r，但是总路径长度 l（途中经过的每边 e 的长度 le 之和）是成本。总收益是 r-l。（为了简化，这里设成本系数为 L）。现在小哥刚刚出发，车上只有一份外卖，箱子最大容量仍设为两份外卖，请问怎么走才能最大化收益？（提示：这里不但要考虑路径长短，还要考虑可能收到送至相同地点的另一单外卖而带来的无额外成本的收益 r。假设 0<=Pc<=min{le/r，1}）。

第三题

a. 马教授的领域内有 n 个不同但是等价的逻辑陈述，A1，A2，...，An，现在需要证明它们是等价的。每个学期，马教授选两个不同的陈述 Ai 和 Aj，以「Ai->Aj」的证明作为研究课题，指导一位本科生完成。假设每个学期只完成一个证明。要注意的是，在「Ai->Aj」和「Aj->Ak」被证明之后，「Ai->Ak」也已经被自动的证明了，因此不能再作为一个新的课题让学生去完成。总之，如果一个课题是之前若干学生已经完成课题的直接推论，则不能作为新课题发给另一个学生。随着越来越多的推出关系被证明，剩下可选择的课题也越来越少。请问，马教授可以最多依次指导多少个学生呢？为什么？

b.H 是一个 n x n 的方阵，其第 i 行第 j 列的元素是 hij，所有 hij的取值集合为{1，-1}，并且 H 的任意不同的两行看作向量是相互垂直的（即，他们的标准内积为 0）。假设 H 有一个 a x b 的子矩阵（1<=a,b<=n），子矩阵内的元素均为 1。请证明 a，b<=n。

c.G 是一个群。e 是该群的单位元。定义 G 的一个子集：

F = { h 属于 G | 存在自然数 m >= 1，使得 hm = e }。

假设集合 F 内的元素是有限多个的。证明：存在一个自然数 n >= 1 使得对所有 g 属于 G 和 h 属于 F，我们都有：

以上就是全部预选赛试题，阿里巴巴数学竞赛官方网站也给出了这些题目的参考答案。

第一题答案

A.709 元人民币。

为了得到这个答案，我们必须要使用其它店铺的优惠券。如果所有的优惠券都来自店铺 A，那么付款金额可以减少到 705，但在实际中，这个是行不通的。下面是如何得到 709 人民币的具体步骤：

下面我们来比较耳机和音箱一起买与耳机和音箱分开买这两种购买方案，其中，分开购买可以获得更小的支付金额，也就是 709 元。

在同一个订单中购买耳机和音箱：

耳机 250 元，加上音箱的 600 元也就是 850 元，由于在店铺 A 每满 60 可以使用一张 5 元优惠券，60*14=840，因此可以在店铺 A 使用 14 张优惠券。此外，电商平台全场提供的满 299 减 60 的优惠券也可以使用。

于是，在同一个订单中购买耳机和音箱总共需要花费的金额为：

850-14*5-60=720 元

耳机和音箱分两个订单中购买：

这种方案最终的花费为 709，具体的购买方法如下：

耳机的价格是 250 元，因此可以凑单一件 49 元的商品，这样就可以使用 4 张 5 元优惠券，以及一张满 299 减 60 的优惠券。算下来需要的花费为 250+49-4*5-60=219 元。

音箱的价格是 600 元，可以使用 10 张满 60 减 5 元的优惠券和 1 张满 299 减 60 元的优惠券。于是需要花费的金额为 600-60-10*5=490 元。

因此，耳机和音箱分别购买需要的总花费为 219+490=709 元。

综上所述，最小花费是 709 元，采用的方案是耳机和音箱分两单购买，并且耳机那个订单要凑单一件 49 元的商品。

B. 问题 1 答案为：如果使用其它店铺的优惠券，那么 x 为 21；如果只使用店铺 A 的优惠券，那么 x 为 25。

问题 2 答案为：如果使用其它店铺的优惠券，那么 x 为 36；如果使用店铺 A 的优惠券，那么 x 为 38。

具体步骤为：

问题 1：为了在你的店铺里面买一副耳机，某个人需要支付的钱数为 250-x+49（凑单品价格）-60（平台提供的满 299 减 60 优惠券）=（239-x）元。对于音箱，我们也用同样的方法计算，得到的这个人需要支付的金额为（540-x）元。为了减少你的店铺在耳机上的花费，x 必须满足的条件为 239-x<=219，或者 x>=21；为了让你的店铺减少在音箱上的花费，x 必须满足 540-x<=490-1，或者 x>=51。当 x 为 21 时，我们可以保证购买耳机是便宜的，但是此时，音箱并不是最便宜的。

问题 2：如果在你的店铺里面买耳机和音箱，那么分两单分别购买耳机和音箱更划算，因为这样可以获得的总折扣金额为 2x。这两个订单的金额分别为（239-x）和（540-x）。它们的总金额肯定比 709 元要小，那么第二个问题的答案是什么？在这里，x 满足的条件为（239-x）+（540-x）<=709-1，或者 x>=35.5。因为 x 必须是整数，所以我们求得这个问题的答案为 x=36。

C. 题目 1 答案：最优价格为

，期望利润为

，i=1，2。在 i 为 1 或者 2 的时候，步骤都是一样的。我们用 R 表示利润这个变量，它随着 S 的变化而变化。公式为：

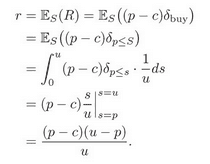
同样的，我们也可以算出期望利润作为产品的利润，（p-c），购买的可能性为 (u-p)/u。

函数

是一个凹二次曲线函数，因此它的极大值点 p*如果在 [0，u] 这个区间取得，则满足条件

，此时，p*=(u+c)/2，如果 c<=u，那么在该点处函数取得最大值。否则，在 p*=u 处取得最大值。

当 p*=(u+c)/2 时，我们可以得到

。

题目 2 答案：价格

的最大值为：

注意到

是关于

的分段函数，分成了三段，我们可以算出每个邻域内的边界点。

同样我们注意到，计算结果并不是唯一的，学生可以画出函数的曲线图，根据这个曲线图来找出正确答案。

不管用什么方法，我们需要三步来计算出

。

步骤 1：定义变量

，计算

的分布并记为

，这个分布并不是均匀分布。

步骤 2：计算期望利润，为

对于

，当

时，有

。

步骤 3：对于每个区间来说，最大值就是期望利润，也就是说，必须要找到

在每个区间的最大值。

当

的取值区间为 [0，u1] 时，

的倒数为

画出函数的曲线或者检查它的二阶导数，可以很容易地看出上面的

的极大值。从

，可以得到

，在这种情况下，

是期望利润的最大值。

采用相同的步骤，我们可以求出在另外两种情况下的

值和它对应的

的值。

题目 3 答案：不一定，没有哪一种策略比其余的策略好。

可以使用两个例子来证明这一点，第一个策略采用的方法比第二个好，第二个策略采用的方式比第一个好。有很多这样的例子，我们就不具体举例了。

第二题答案

题目 a 答案：最短的路径长度是 16。获得这个数值的方法是采用下面的顺序进行送餐：

A -> B2 -> C2 -> B1 -> B3 -> C3 -> C1

具体来说，有两种送餐路线可以使路径长度为 16，它们有轻微的不同，即：

路线1：

路线2：

这两条路线都可以经过所有的取餐点。

罗列出所有的路线并计算他们的路径长度是一件非常繁琐的工作，然而，在这个题目里面我们不需要这样做。因为这个图是一个平面图，并且路线的方向和目的地的距离总是 90 度。这就意味着，任意两个点之间的最短路径都是很容易求得的。

要手动计算出这个问题的答案，首先可以大致估算一下 {B1,C1,B2,C2,B3,C3} 的顺序并计算出路径长度。实际上，有很多排序方式可以让路径的长度为 17，如果你算出的值比这个稍微高一点儿，那么就是一个好的排列顺序。这个距离是最短距离的上限。然后罗列 {B1,C1,B2,C2,B3,C3}的顺序并计算出路径长度，一旦长度达到 17，就排除这个路线。当你找到一条总长度为 16 的路线时，上限改为 16，这个策略叫做分支界限法。

题目 b 答案：对于问题 1 来说，P1 + P2 + ... + Pm。我们让

的取值为 0 或者 1，边界为

，对于 i = 1,2,...,m 来说，我们可以通过下面的方法来计算答案：

对于问题 2 来说，是

。在这里，（1-Pi）是在 ei 处没有外卖的概率，并且我们可以根据概率论知识知道，

是整个路线上都没有外卖的概率，因此，1 减去这个概率值是最少可以在这条路线上取到一个外卖的概率。同时，可以使用条件概率来得到的递归公式为，在e1之后最少可以获得一单新外卖的概率为

，也就是

，通过不断的递归，可以得到最终的式子为

，这个递归也是一个正确答案。

上面的两个答案都可以和下面这个式子等同：

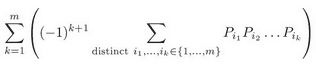
题目 c 答案：假设我们不考虑一般性的情况，现在有 T 个节点，并且 T 是目的节点。首先，对于每个节点 i，找到去 T 的最短路线和对应的路线长度

（如果具有相同长度的不同路线之前有相互关系，一定要解除他们之间的关系）。对于 i=T，我们有

。

接下来，使用

，在每个节点计算最优预期回报

，使用下面给出的极大值公式（3）来计算。对于

，假设

是 i 的相邻节点，并且在该点处能取得极大值（同样地，如果节点之间有关联，打破这个关联）。

外卖小哥的最优路线被下面的每个点决定了：在节点 i 的时候，如果外卖小哥还没有拿到额外的一单，那么移动到

；如果外卖小哥拿到了额外的一单，那么他车上的外卖箱子已经装满了，因此只需要走从 i 到 T 的最短路线。

注意到上面的路线并不是事先计划好的，而是由外卖小哥自己决定的。也就是说，这是一个策略问题。这种方式比事先计划好路线要好，因为是否会有额外的外卖单是未知的，而这会影响路线、影响到 T 的距离。

当外卖小哥在节点 i 并且取到了第二个外卖的时候，外卖小哥决定去哪里采用的方法是去这个地方获得的收益的期望值，这个收益值又被获取外卖的可能性和到 T 节点的距离所影响。

定义在取到额外的外卖前，在节点 i 的最优预期收益为

。当 i=T 时，我们让

，这个是固定的收益。假设我们计算了 i 的相邻节点

。在节点 i 的时候，如果我们要移动到节点 j，那么预期收益将会变成：

，如果在 i、j 两点之间出现外卖；

，如果在 i、j 两点之间不出现外卖。

设 i、j 之间的边长度为

，则有：

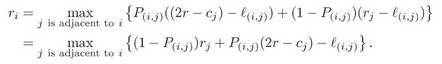
（3）

这就是众所周知的贝尔曼方程。

根据

和式子（3），我们可以计算出

，你可以使用动态规划或者更具体的图，贝尔曼·福特算法或者迪杰特斯拉算法（请看下面的说明）。它们都从

开始，并且决定了

这个集合里面的元素。

对于

或者

，必须要避免「正面奖励」的存在，这可以避免外卖小哥为了获得额外的报酬而不停地在这些路线走来走去，直到取到额外的一单外卖这种不现实的情况。

我们注意到，在实际中，学生们更倾向于使用迪杰特斯拉算法。这种算法要求边长必须是非负的值。因此，如果一个人使用这个算法去计算

，必须要满足这个条件。对于我们的这个问题，这里必须要满足：

（4）

在满足假设条件

的条件下，这种情况确实存在。为什么呢？既然最坏的情况也就是外卖小哥沿着最短路径到达 T 节点处（而不是选择使收益最大化的节点），我们可以得到：

于是可以得到第二个不等式：

第一个不等式的假设条件是

不大于

，我们可以结合上面的不等式得到式子（4）。

第三题答案

题目 a 答案：我们首先指导 0.5(n+2)(n-1) 个学生，下面，我们将证明这个答案。

解释：首先，(n-1) 个学生证明 A1->Ai，其中 i 为 2 到 n 的整数；然后，(n-2) 个学生证明 A2->Ai，其中 i 为 3 到 n 的整数。一直这样做，直到最后一个学生证明 An-1->An。

然后，(n-1) 个学生证明 An->An-1，An-1->An-1，...，A2->A1。它们的总数为：

让

。

最优性证明：假设图 G=（N，E）的节点为 N={1,2，...，n}，其有向边为 E={（i，j）|Ai -> Aj已经被证明了}。完成一个课题，意味着给 E 加上一条边。

假设 E': = { （i, j ) | 其中，Ai -> Aj 和 Aj -> Ai在前面已经被证明了 } 是对偶边，是集合 E 的子集，子图 G’=（N，E'）最多有 2(n-1) 个有向边；否则，必然存在一些对偶边包含无效课题。

G 最多有 n(n-2)/2 对节点，去掉对偶边上的节点，正如前面所证明的，此时最多有 2(n-1) 个有向边，因此最多有 (n-1) 对有向边，也就是说，有 n(n-1)/2 - (n-1) = (n-2)(n-1)/2 对节点之间是单向边或者是没有边的。因此，最多有 (n-2)(n-1)/2 个单向边。因此，加上单向边和对偶边的最大数得：