四种常见排序算法的对比和总结 插入排序、归并排序、快速排序、堆排序
目录
一、排序算法的时间复杂度
二、排序算法是否是原地排序
三、排序算法的额外空间
四、排序算法的稳定性 Stable
五、总结
这里我们要总结的排序算法主要有4个,分别是插入排序Insertion Sort、归并排序Merge Sort、快速排序Quick Sort、堆排序Heap Sort。
下面是四种排序算法具体介绍的文章。
插入排序:
十分重要的O(n^2)级别排序算法 插入排序-InsertionSort
归并排序:
使用递归和非递归实现 归并排序-MergeSort
快速排序:
快速排序QuickSort-基本实现和简单优化
快速排序优化-随机化快速排序法
快速排序优化-双路快速排序法 Quick Sort 2 Ways
快速排序优化-三路快速排序法 Quick Sort 3 Ways
堆排序:
堆排序Heap Sort实现详解和优化
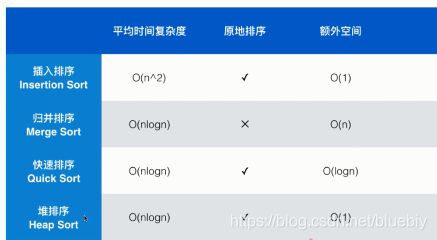
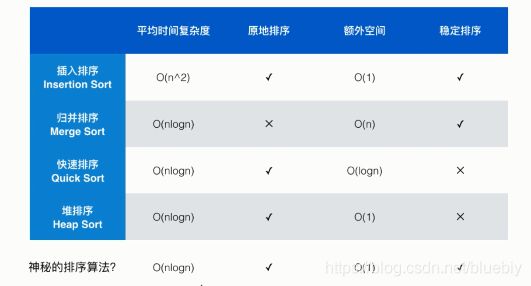
一、排序算法的时间复杂度
对于三种时间复杂度是O(nlogn)来说,他们有常数上的差异,对于这个常数上的差异,快速排序相对占优。总体而言,快速排序是更加快的一种排序算法。正因为如此,一般系统级别的排序,都是使用快速排序来实现的。
二、排序算法是否是原地排序
插入排序、快速排序和堆排序这三种排序都可以直接在数组上交换元素,进而完成排序。而归并排序并不可以,它必须开辟额外的空间,来完成归并的过程,才能完成归并排序。正因为如此,如果一个系统对空间相对比较铭感的话,归并排序可能并不适合。
三、排序算法的额外空间
对于插入排序和堆排序来说,由于他们可以直接在数组上交换元素来完成,所以空间复杂度是O(1)。也就是常数级别的空间,不管你要排序的数组有多少个变量,只需要额外开辟几个临时的变量空间就能完成。
而归并排序需要O(n)的额外空间来完成归并的过程(其实是O(n + logn),logn被忽略了)。
快速排序需要的额外空间是O(logn),因为对于快速排序来说,我们采用递归的方式来进行排序,这个递归的过程一共有logn层,所以需要有logn栈空间来保存每一次递归过程中的临时变量,以供递归返回的时候临时使用。为此我们需要注意,快速排序虽然是一种原地排序,但是所需要的额外空间是O(logn)级别的。
四、排序算法的稳定性 Stable
插入排序和归并排序属于稳定排序,而快速排序和堆排序不属于稳定排序。
稳定排序:对于相等的元素,在排序后,原来靠前的元素依然靠前。
换句话说 相等元素的相对位置没有发生改变。
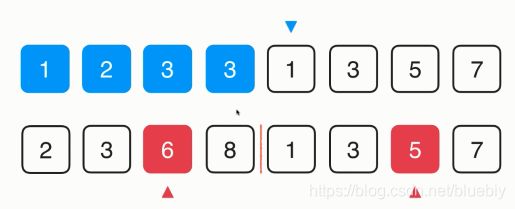
我们简单的看一下如下图的例子。
比如说我们要对如上的数组进行排序,这个数组中有三个相同的元素3,把这三个元素分别用三种颜色红、绿、蓝标记出来。在初始的数组中这三个元素3虽然大小相等,但是它们是按照红绿蓝这样的顺序排列的。那么排序以后这三个元素3肯定是放在一起,并且在正确的位置上,更重要的是三个元素3依然是按照红绿蓝的顺序排列的,如下图所示,那么我们就管这个排序算法叫做稳定排序算法。
稳定排序算法在我们生活中有很多的用处。比如说学生的成绩单,在初始的情况这个成绩单是按照学生姓名的字典序来进行排序的,现在想按学生的分数进行重新排序,稳定的排序就能做到按照学生的分数排序完毕以后,对于相同分数的学生,他们之间依然是按照学生姓名的字典序来进行排序的。
我们先来看看两种稳定排序。
1.插入排序,它为什么是一种稳定的排序?我们假设插入排序运行到一定程度,到了如下图所示的样子。元素3、6、8已经按照插入排序的规则排序完成,前面部分已经是有序的。
现在我们要考察第4个元素3应该放在什么位置?我们想一下插入排序的操作,元素3往前遍历,找到第一个小余等于它的元素,插入到该元素的后面。
3和8比较,3小余8,3和8交换位置。
3和6比较,3小余6,3和6交换位置。
现在3和3比,我们在代码实现的时候,只有在小余的情况下,才交换位置。如果大于等于的话就不动。这样一来如果后面的元素和前面的元素是相等的话,那么后面的元素永远不会超越前面的元素,从而保证了排序算法的稳定性,插入排序算法是稳定排序算法。
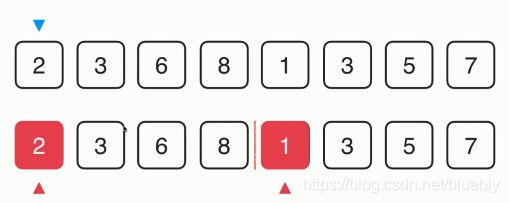
2.归并排序,它为什么是一种稳定的排序?归并排序的归并的过程中,左右两部分已经有序了,现在要把它们归并到一起,我们来模拟一下这个过程。
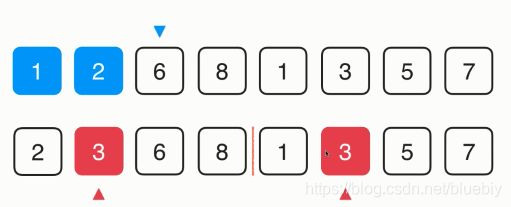
比较2和1,1比2小,1放在第一个位置,相应的指针移动。
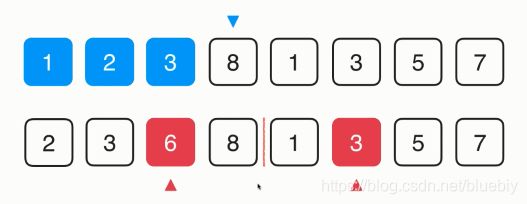
比较2和3,2比3小,2放到第二个位置,相应的指针继续往后移动。
之后比较3和3,这是两个相等的元素,我们再归并的过程中可以判断,只有后面的元素小余前面的元素的时候,才将后面的元素放入最终的归并数组中。否则的话前面的元素小余等于后面的元素,前面的元素放入最终的归并数组中。
这样一来对于相等的元素来说,排在前面的元素在归并之后,也将继续排在前面。而排在后面的元素在归并之后仍然排在后面。这样使得归并排序算法也保持了稳定性,归并排序算法是稳定排序算法。
上面介绍了为什么插入排序和归并排序是稳定排序算法。由于插入排序是稳定的,所以我们在给归并排序做优化的时候,当n小到一定程度的时候,我们改用插入排序来进行排序,依然是的归并排序保持了稳定性。
另外我们也认识到了,所谓排序算法的稳定性,是和具体实现相关的。也就是说你实现的不好的话,很有可能将插入排序和归并排序,实现成了一个不稳定的排序算法。这一点我们要注意了。
3.快速排序算法不是稳定排序算法。快速排序每次要选标定点,标定点随机选着。这个过程就很有可能使得对于相等的元素来说,本来应该在后面的元素,排到了前面。
4.堆排序算法不是稳定排序算法。堆排序将整个数组组建成堆的过程中,也有可能破坏相等元素的先后顺序。
有兴趣的同学可以自己举一个反例,来说明快速排序和堆排序他们并非是稳定排序的。
这里我们还需要注意,排序算法的稳定性,可以通过自定义比较函数,使得排序算法不存在稳定性的问题。比如说就想使用快速排序,但是又要顾及稳定性,那怎么做呢?
我们还是以之前学生的排序为例,排序主要的键值是成绩,我们希望通过排序算法的稳定性,来使得相同成绩的学生按照姓名的字典序来排序的。但如果我们使用的排序算法不稳定的话,那么我们只好在比较的过程中,加入对学生姓名字符串的字典序的比较。具体实现如下。
使用这样的方式,在比较函数中相当于多比较了一下,正因为如此效率有所损耗。不过在一般的情况下,我们使用现在的计算机,这个效率的损耗完全是可以接受的。只是在一些对性能非常敏感的情况下,或者对于这种比较的函数不太好更改的情况下,我们又希望排序的结果具有稳定性,那么稳定的排序就具有了意义。
插入排序和归并排序都是稳定排序算法,通常在系统级别的类库中,我们要实现一个稳定的排序,通常选着的是归并排序算法。
五、总结
本篇将这种排序算法比较完成了,当然还有一些其他的排序算法没有分析,比如冒泡排序、希尔排序等等,感兴趣的可以根据这些指标自己去分析一下。本篇由于篇幅的关系,只分析了这些比较经典的基于比较的排序算法。
我们需要注意一点,对于这四个指标来说,每种排序都各有优劣各有侧重,但是是不是存在一种神秘的排序算法,对于这些指标都是最优的呢?
这个最优的排序算法,在平均时间复杂度上是O(nlogn)级别的,最好对于有序的情况还能降成O(n)级别的,对于任何情况下都不可能退化成O(n^2)级别的。同时他是个原地排序,额外空间O(1),而且还是个稳定的排序。
我们可以看到上面四种排序都不符合最优的标准,是不是有一个神秘的排序算法符合这个标准?到目前为止计算机科学家们还没有发现这样一种排序算法,不过理论上这种排序算法是存在的。排序算法这样一个基本的任务,经过了这么多年的研究,其实还存在真空,还有很多值得挖掘的东西。