--AutoLeaders--2023全栈组系列教程 第2章 Python新手上路

配置好Python环境后，让我们开始学习一些Python的基础语法吧。全栈组的二面考核，将会通过一些基础的Python编程题目，来考察大家的编程能力、自学能力、解决问题能力。加油吧！天道酬勤，组长在这里祝福各位都能取得好成绩。

目录

2.1 Python 基础知识学习

2.1.1 教程向导

2.1.2 刷题网站推荐

2.1.3 AL - OJ使用方法

2.1.4 组长寄语

2.2 进阶 : Python竞赛指导

2.2.1 泰迪杯

2.2.2 蓝桥杯

a. 什么是 OI 赛制

b. 常考知识点

c. 核心算法与数据结构

模拟     枚举     深度优先搜索     数据结构 - 栈

数据结构 - 队列     广度优先搜索     动态规划     简单图论

d. 算法技巧指导

贪心法     二分查找     二进制枚举

记忆化搜索     打表

---

2.1 Python 基础知识学习

2.1.1 教程向导

【Python教程 - 廖雪峰的官方网站】

【本博客分享的资源中有全栈组为新人提供的学习资料，如有需要可以下载学习】

关于python基础语法的资料已经比较齐全，师兄在这里就不作重复工作了，请各位按照向导学习python基础知识，大家还可以到B站找一些视频教程来辅助学习。

可以看一下往届师兄师姐推荐的视频 【[小甲鱼]零基础入门学习Python】 看到P28就差不多了

2.1.2 刷题网站推荐

【AL - OJ】 AutoLeaders自己搭建的OJ，二面题目将会在这里发布

【洛谷 luogu】

【力扣 LeetCode】

【拼题A PTA】

大家记得到我们俱乐部的OJ上注册账号并完成我们发布的练习题目，练习完成情况将会计入二面的成绩。

2.1.3 AL - OJ使用方法

1、从师兄师姐提供的链接进入oj  (不公开在博客，防止oj受到攻击)

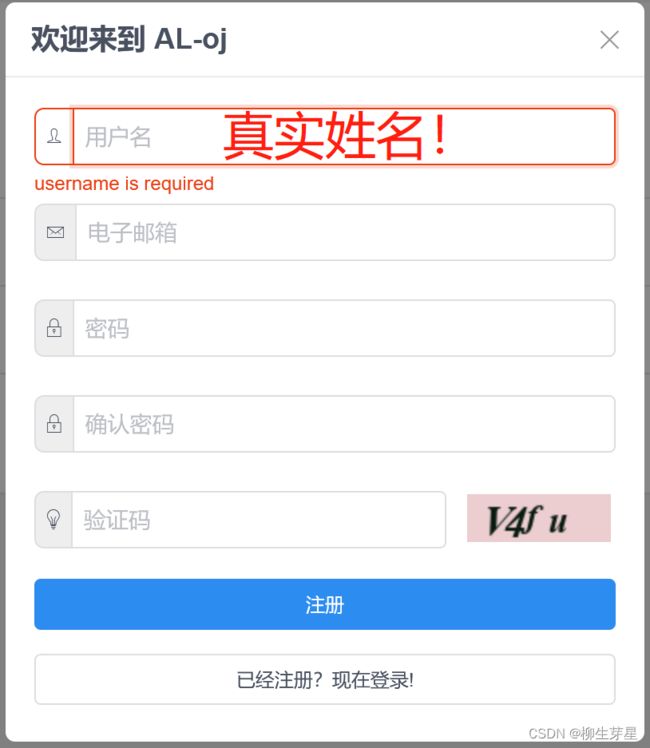
之后请点击左上角的注册

​

2、在注册信息界面，请大家在用户名的地方输入自己的真实姓名。(一定要真实姓名，不然成绩无效并被计入黑名单)

​

3、按照要求填写好其他信息后点击注册即可，然后就能够登录啦！

4、登录之后，在屏幕上方有一个名为 “练习&比赛” 的链接

​

5. 点击之后选择对应组组的招新作业，就是大家需要在二面之前需要完成的内容了

6. 点进去之后，在屏幕的右手边有个 “题目”，点击进去就能看到所有的作业啦

7. 题目的提交

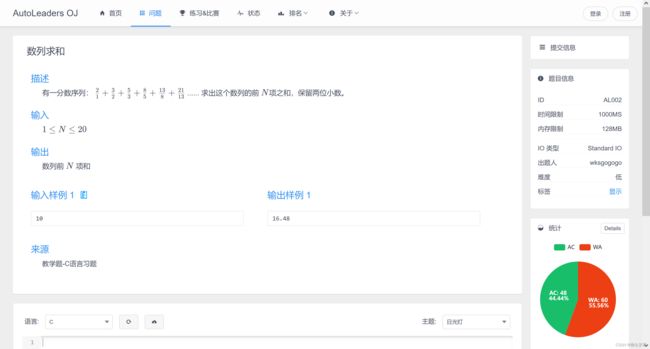
我们随便打开一道题作为演示，比方说数列求和这道题

​

大家看了题目之后，可以在自己电脑上安装的编译器上将代码写下来，自行测试样例

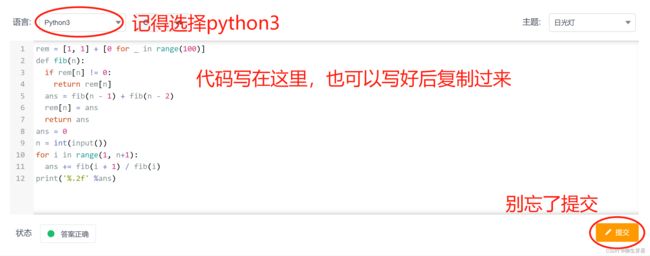
然后将代码复制到OJ上，点击代码左上角“语言”的下箭头，选择python3，最后点击提交

2.1.4 组长寄语

相对于其他编程语言，Python的入门门槛是比较低的，但是没有大量的练习、深入的钻研，是没法掌握它的。我们给出的练习题，以及二面的考试题，其实都是python中非常基础的内容，但是由于大部分同学没有接触过编程，可能会在学习过程中屡次遭遇困难。没有关系，当前阶段遇到的问题，都是可以通过查资料解决的。组长希望大家能练就良好的查找资源的能力，这对于以后的学习和竞赛非常有帮助。

偶尔有同学来问组长 Python 的学习方法，在当前阶段，我的建议是以解决 OJ 题目为驱动力。在解题时，思考能否运用已有的知识来解决，如果不能，或者有新的思路但不知道怎么实现，就查找资料寻求办法。随着解决题目的数量增加，掌握的知识也自然会变得全面。

Python基础的内容到这里就结束了，下面是一些进阶内容。(如果你还在准备二面，就快快去刷题吧，下面的内容需要一定的基础才能理解，建议二面结束后再来阅读)

2.2 进阶 : Python竞赛指导

在学习了Python基础之后，我们就具备了使用Python解决简单问题的能力。泰迪杯和蓝桥杯是两个门槛和获奖难度都比较低的竞赛，很适合竞赛新手入门。这两个比赛都给了Python选手大展拳脚的机会，这里给出一些指导，希望能帮助各位顺利获奖。

2.2.1 泰迪杯

这个比赛主要考验的是数据分析能力，三人一队，一般而言，这样分工会比较合理：

1位选手专门负责撰写论文，2名选手使用Python进行数据分析

泰迪杯技能赛的题目多变，需要的技术不固定，但是有一些知识是python数据分析中的核心知识，组长将会通过下面这篇博客教学 Numpy、Pandas 和 Matplotlib 三个 python 库的基本使用方法

【AutoLeader 泰迪杯竞赛指导】

其他推荐的参考资料：

2.2.2 蓝桥杯

这是一个OI赛制的个人算法竞赛，有很多个赛道，比较推荐的有C/C++赛道，也可以选择Python赛道，控制组的同学可能会选择单片机赛道。

组长只参加过Python赛道的比赛，下面通过一些例题，带大家学习一些Python的基础算法。（师兄的战绩是PythonB组国三，实力有限，只能领大家入门，想要取得好成绩，还需更加深入地钻研！）

我把接下来的指导中涉及到的题目整理到了 luogo 题单中，需要者自取 :【我的练习题整理】

a. 什么是 OI 赛制

【赛制介绍：ACM OI 与 IOI】

蓝桥杯是OI赛制，这意味着你不需要非得写出“正解”才能得分。在该赛制下，每一道题目有多个测试点，通过的测试点越多，得分也就越高。因此打这类竞赛是有一些得分技巧的，在没有思路时，可以通过一些 “暴力算法” 获得部分分数

b. 常考知识点

技巧类	核心算法类	数据结构类
基本不会单独拎出来考，会穿插在其他题目中作为技巧出现	通常作为核心考点，比较重要	核心算法通常涉及到一些数据结构，需要掌握这些数据结构的特点和构建方法
贪心、二分、递归、二进制优化	模拟、枚举、深度优先搜索、广度优先搜索、动态规划、简单图论	栈、队列、邻接表、邻接矩阵

c. 核心算法与数据结构

模拟

“模拟”可以说是一种思想，用程序模拟题目要求的相关过程，就像是依葫芦画瓢。一般来说，这类题目不会有太深的思维难度，但是代码量和操作数会较多。例如：【P1003 [NOIP2011 提高组] 铺地毯】https://www.luogu.com.cn/problem/P1003

这就是一道经典的模拟题，我们可以通过模拟每张地毯覆盖在地面的过程：每铺一张地毯，就判断这个地毯是否覆盖了指定的坐标 (x,y)，如果覆盖了则更新答案

n = int(input())

# 由于指定的坐标(x,y)是最后给出的,我们先将地毯的位置信息存进列表m中备用
m = []
for i in range(n):
    m.append([int(j) for j in input().split()])

# 坐标在这里才给出,记录到变量x, y中
x, y = map(int, input().split())

# 题目要求如果指定点没有地毯覆盖则输出 -1,那不妨将答案的初始值设置成 -1
ans = -1

# 接下来就是模拟的过程,既然求的是最上面的地毯,那我们可以倒着模拟
# 因为排在后面的地毯必然是覆盖在最上层的,一旦得出结果,就不用考虑下层的地毯了
for i in range(n-1, -1, -1):
    X, Y, Lx, Ly = map(int, m[i])
    # 当发现某块地毯能覆盖指定点,更新答案,终止模拟
    if X <= x <= X + Lx and Y <= y <= Y + Ly:
        ans = i + 1
        break
print(ans)

这道题目比较简单，蓝桥杯如果考到了模拟题，大概率会比这道难。具体表现在情况更复杂，操作数更多，一般来说，不会做不出来，但是会消耗掉很多时间。这里给出一些练习题，希望大家多多练习，锻炼思维能力，争取提高这类题目的解题速度

【P1308 [NOIP2011 普及组] 统计单词数】  【P1724 东风谷早苗 】

【P4924 [1007] 魔法少女小Scarlet】               (省赛大概会比这个难一点)

【P1065 [NOIP2006 提高组] 作业调度方案】  (国赛如果考了模拟，大概会到这个难度)

枚举

枚举是十分经典且重要的算法，俗话说，计算机最擅长的事情就是重复，对于某些问题，直接求解比较困难，但是我们可以通过不断试错，直到找出正确答案，来达到求解问题的目的。

【P2089 烤鸡】https://www.luogu.com.cn/problem/P2089

这道题主打的就是一个穷举，最简单暴力的方法：穷举每样配料放的质量，符合要求则记录，最后输出记录总数和记录内容。接下来请欣赏暴力穷举：

n = int(input())
# 当不符合要求时直接输出0
if n >= 31 or n <= 9:
    print(0)
# 穷举每样调料的质量,注意题目要求:按字典序排列
else:
    ans = []
    for l0 in range(1,4):
        for l1 in range(1,4):
            for l2 in range(1,4):
                for l3 in range(1,4):
                    for l4 in range(1,4):
                        for l5 in range(1,4):
                            for l6 in range(1,4):
                                for l7 in range(1,4):
                                    for l8 in range(1,4):
                                        for l9 in range(1,4):
                                            # 当枚举到符合要求的情况时记录到列表ans中
                                            if l0 + l1 + l2 + l3 + l4 + l5 + l6 + l7 + l8 + l9 == n:
                                                ans.append([l0,l1,l2,l3,l4,l5,l6,l7,l8,l9])
    print(len(ans)) # 输出记录总数
    # 输出记录内容
    for ans_ in ans:
        j = [str(i) for i in ans_]
        print(' '.join(j))

穷举是一种简单且重要的解题方法，上述代码是比较“无脑”的穷举 (枚举所有情况)，其实有些时候我们不需要枚举所有情况，或者我们可以以一定的规律进行枚举，以求更快地找到题解。这时候，就可以使用“更高级”的枚举：搜索

深度优先搜索

深度优先搜索，又称 DFS (Deep First Search)，这是蓝桥杯竞赛中十分重要的考点！务必要掌握，下面这个视频讲解了深搜的原理，先不用考虑怎样用代码实现，重点理解 DFS 的运行过程

【深度优先搜索的原理分析】

看完了视频，大家对于深搜的运作过程已经有了一定的了解，那么怎么用代码实现呢？

其实 DFS 的难点就在于 “回溯” 的实现，我们怎样做才能让程序的状态 “回退” 到上一步呢？

实现回溯有两种比较简单的方法：1、使用递归进行回溯  2、利用数据结构：“栈”进行回溯

这里先介绍使用递归实现回溯的方法，我们先来看以下这段代码，来理解为什么递归具有回溯的性质：

def test(n):
    # 为了防止无限递归,我们在n > 3时开始返回
    if n > 3:
        print("递归第{}层,到终点了,返回吧".format(n))
        return
    print("递归第{}层".format(n))
    # 递归,进入下一层
    test(n + 1)
    # 执行完上面那句递归后,又返回了当前层
    print("回来了!递归第{}层".format(n))

test(1)

这段代码的运行结果如下，可以看到，在进行到第4层时，递归开始返回，渐渐回溯到了第1层

利用递归能够回退的性质，我们可以用递归实现深度优先搜索

在刚刚给出的视频链接中，其 2P 用C++实现了一个DFS走迷宫的程序 【DFS走迷宫 - 代码实现】

可以参考这个视频，用 Python 写一个走迷宫的深搜程序，这里给出组长用Python写的参考代码

【下面的代码会基于这个问题 : P1605 迷宫】

# 输入迷宫长宽、障碍数
n, m, t = map(int, input().split())
# 创建一个 n * m 的二维数组,代表迷宫
maze = []
for i in range(m):
    maze.append([0 for _ in range(n)])

# 输入起点、终点坐标
startx, starty, endx, endy = map(int, input().split())
# 输入t个障碍的坐标信息,将相应点标记
for i in range(t):
    x, y = map(int, input().split())
    maze[y - 1][x - 1] = 1  # 将对应点标记为1,代表不可通过

ans = 0
# 减少代码量的小技巧,视频里有提到
dx = [1, -1, 0, 0]
dy = [0, 0, 1, -1]

# 深搜函数本体
def DFS(x, y):
    global maze, ans  # 请自行搜索 python 中 global 的作用
    # 当到达终点时,ans加一
    if x == endx - 1 and y == endy - 1:
        ans += 1
        return
    # 向四个方向试探
    for i in range(4):
        X, Y = x + dx[i], y + dy[i]
        # 判断是否越界
        if 0 <= X < m and 0 <= Y < n:
            # 判断是否可通过
            if maze[Y][X] == 0:
                maze[Y][X] = 1 # 标记为不可通过
                DFS(X, Y)
                maze[Y][X] = 0 # 重新标记为可以通过
# 从起点开始深搜
DFS(startx - 1, starty - 1)
print(ans)

走迷宫是 DFS 最经典的应用场景，当然不仅仅是走迷宫，很多问题都可以用深搜来解决，这里给出一些练习。DFS 这个算法，需要多练才能掌握，否则在竞赛现场很可能有思路但是写不出代码。

【P1157 组合的输出】  【P2404 自然数的拆分问题】

【P8601 [蓝桥杯 2013 省 A] 剪格子】  【P1596 [USACO10OCT] Lake Counting S】

（枚举一节中给出的例题《P2089 烤鸡》也可以用 DFS 来解决，大家可以试试看）

数据结构 - 栈

栈 (stack) 是一种 “先进后出” 的数据结构，利用栈的性质，我们可以解决一些问题

【数据结构 - 栈 及Python实现】

在这个视频中，介绍了栈的特点，后面也用 Python 面向对象的方式实现了栈这个数据结构。考虑到一些同学没有接触过面向对象，且算法竞赛中不太需要面向对象，这里给出不基于面向对象的实现方式 : 定义一个列表，然后只使用 append 和 pop 方法操作它

stack = [] # 定义一个栈
# 使用append方法实现“入栈”
stack.append("object")
# 通过索引查看栈顶元素
print(stack[-1])
# 使用pop方法实现“出栈”
stack.pop()
# 通过列表长度判断栈是否已空
if len(stack) == 0:
    print("the stack is empty")

那么栈有什么用呢？上面给出的视频后面的续集就使用栈解决了“简单括号匹配”、“十进制转二进制”的问题。这里也给出一道练习题 【P1944 最长括号匹配 】 ，这道题目也可以使用动态规划解决，详情参考洛谷提供的题解

还记得之前提到过，可以使用“栈”来实现 DFS 吗，其实栈的先进后出的特点，刚好满足回溯的性质。要“前进”时，进行入栈操作；想“回退”时，使用出栈操作

想要更深入地了解如何使用栈实现深搜，可以参考这个视频【使用栈解决迷宫问题】

数据结构 - 队列

队列 (queue) 经常和栈进行对比，与栈不同的是，队列是一种“先进先出”的数据结构，和现实中的排队很相像，广度优先搜索就是基于队列实现的。

【数据结构 - 队列 及Python实现】

这个视频介绍了队列的特征及简单应用，还给出了Python面向对象实现队列的方法，照例给出比较简单的实现方式：定义一个列表，只使用 append 和 pop(0) 方法操作它

queue = [] # 定义一个队列
# 利用append完成入队操作
queue.append("object")
# 利用pop(0)完成出队操作
# 注意pop(0)这个方法是有返回值的,会将被删除的元素返回
a = queue.pop(0)
print(a)

视频中也提到，使用这种方式实现队列，会使入队和出队的时间复杂度呈现：一个为O(n)另一个为O(1) 的特点，其实有一种叫作环形队列的实现方式，能使入队和出队都为O(1)的时间复杂度。不过竞赛中使用上述的实现方式就足够了，学有余力，想要拓展的可以自行了解

值得一提的是，栈和队列都可以使用Python中的一个原生数据结构“列表”来实现。其实列表是一个十分强大的数据结构，基于列表，我们可以实现一些复杂的数据结构，例如树和图。至于怎么实现，就是后话了。下面我们来讲一下在蓝桥杯竞赛中，队列最重要的应用方式

广度优先搜索

广度优先搜索，又称 BFS (Breadth First Search)，同深度优先搜索一样，在蓝桥杯竞赛中是非常重要的考点！接下来通过一个视频了解一下广搜的运行过程

【BFS 广搜解决迷宫问题】

该视频使用 C++ 实现了走迷宫的广搜代码，这里给出组长使用 Python 写的广搜代码

# 用一个二维数组表示迷宫
maze = [[0, 0, 1, 0], 
        [0, 0, 0, 0], 
        [0, 0, 1, 0], 
        [0, 1, 0, 0], 
        [0, 0, 0, 1]]

# 定义一个队列
queue = []
ans = -1
dx = [1, -1, 0, 0]
dy = [0, 0 ,1, -1]

# 输入起点和终点
startx, starty, endx, endy = map(int, input().split())
queue.append([startx, starty, 0]) # 将起点入队
maze[starty][startx] = 1 # 将起点标记为不可通过,防止走回头路

# 广搜函数本体
def BFS(x, y, step):
    global maze, queue
    # 向四个方向试探
    for i in range(4):
        X, Y = x + dx[i], y + dy[i]
        # 判断是否越界
        if 0 <= X < len(maze[0]) and 0 <= Y < len(maze):
            # 判断是否可通过
            if maze[Y][X] == 0:
                # 如果可通过则入队,并标记该格为不可通过
                queue.append([X, Y, step + 1])
                maze[Y][X] = 1
# 当队列非空时持续执行广搜
while len(queue):
    # 将队首元素出队
    x, y, step = map(int, queue.pop(0))
    # 当到达终点时,记录答案,停止广搜
    if x == endx and y == endy:
        ans = step
        break
    # 没有找到答案时则继续广搜
    BFS(x, y, step)

print(ans)

与深搜不同的是，广搜大部分时候不会考虑到所有情况 (深搜在不进行剪枝的情况下，会考虑所有情况，这时候和穷举很像)，所以在询问：“从起点到终点有多少条可行的路径”时，不适合用 BFS 来解题。不过由于其只考虑部分情况的特点，在求最短路时，广搜常常会比深搜要快得多

这里给出几道 BFS 练习题，再次强调，深搜和广搜是蓝桥杯竞赛里很重要的考点，务必熟练！

【P1162 填涂颜色 】  【P1443 马的遍历 】  【P8662 [蓝桥杯 2018 省 AB] 全球变暖 】

动态规划

当需要求解一个问题的最优解或者最优策略时，动态规划算法 (常称作 dp) 是一种非常有效的方法。它可以将原问题分解成若干个子问题，并且这些子问题之间存在重叠，因此它可以通过保存子问题的解来减少重复计算，从而提高算法效率。听起来有些抽象，其实所谓动态规划，就是一种优化后的爆搜，我们来通过一道例题来理解一下

【P1216 [USACO1.5] [IOI1994]数字三角形 Number Triangles 】https://www.luogu.com.cn/problem/P1216不考虑时间复杂度的话，这道题显然是可以使用 DFS 来做的，把每条路径的结果用搜索计算出来，再进行比较取最值即可获得答案。但是使用搜索的时间花销是很大的，当数字三角形的层数增多时，会导致花费时间指数级增长。

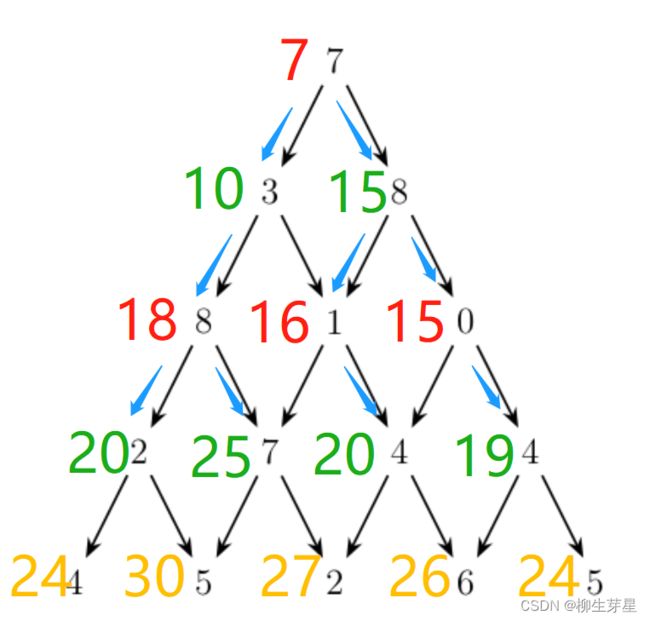
让我们来看看动态规划是怎么做的，以题目样例为例，我现在想求到达红圈中的点的最大值

想要求到达红圈时取得的最大值，我们就要考虑从哪条路走到红圈最优，可以看到有两条路可供选择 (绿色箭头)。那到底要选哪条路啊？我们来看看从起点走到左边的"3"最大能取多少，显然是【7 + 3 = 10】；那从起点走到右边的"8"呢，显然是【7 + 8 = 15】。这时候，我们通过 10 < 15 知道了，选择右边那条路更好，也就得到了从起点到红圈的最大值 : 【15 + 1 = 16】

在上面的过程中，我们想要求到达红圈时的最大值，然后发现比较困难，于是我们把这个问题分解成了两个子问题 : 走到左边的"3"最大值是多少？走到右边的"8"最大值是多少？而这两个子问题相对于原问题来说，更简单易求。其实不仅是这个红圈，在上述图的任意一点，都可以通过逐步分解成更简单的子问题来求解。例如在最底层黄圈标记的点，就可以分解为左右两条路 (蓝色箭头) 哪条更好；左右两个点又可以再往上分解，直到分解到可解的情况。

应用这个思想，我们可以从上往下梳理出每个点能取得的最大值

最底层标黄色的结果中，我们取最大值"30"，即可得到所求的答案，那么代码如何写呢，下面是一段简单示例

# 输入部分
n = int(input())
triangles = []
for i in range(n):
    triangles.append([int(i) for i in input().split()])

# 动态规划
for i in range(1, len(triangles)):
    for j in range(len(triangles[i])):
        # 左右边界特殊考虑,也可以在输入部分向每一层两边添加“0”,这样就不用特殊考虑了
        if j == 0:
            triangles[i][j] += triangles[i - 1][j]
        elif j == len(triangles[i]) - 1:
            triangles[i][j] += triangles[i - 1][j - 1]
        # 中间的点要考虑左右两条路
        else:
            # 这句代码常被称作“状态转移方程”
            triangles[i][j] += max(triangles[i - 1][j], triangles[i - 1][j - 1])

print(max(triangles[-1]))

趁热打铁，来做一些练习吧！

【P1002 [NOIP2002 普及组] 过河卒 】  【P8707 [蓝桥杯 2020 省 AB1] 走方格 】

(前面给出的题目《P1944 最长括号匹配》也是可以用 dp 解决的，大家可以尝试一下)

动态规划的应用场景很多，除了上面的类似“寻找最优路径”的应用，还有一个很经典的题型 : 背包问题 (背包问题的思维难度较高，但是蓝桥杯尤其喜欢考，有心获奖者务必克服困难掌握背包问题)

我们先从最简单的 01背包 开始，这里给出习题与资料 【一道题入门01背包问题】

【P1048 [NOIP2005 普及组] 采药 】  【P1510 精卫填海 】

除了01背包，还有几种背包问题，如完全背包、多重背包 ...... 这些问题都展开讲的话会占用太多篇幅，就请大家自行寻找资料学习

简单图论

蓝桥杯考察图论基本上是板题 (也不简单的)，很少与其他算法结合，因此可以作为一个独立的板块来备考。

很多关于图论的题解都教得不错，但是基本上是用C/C++来讲的。组长接下来讲解如何使用 Python 实现树和图两种数据结构

【什么是树】  【树结构相关术语】在讲解树的实现方法前，先了解一下树结构的一些相关概念

树的实现 : 链表

在 Python 中，可以使用嵌套列表来实现树，这种方法不需要使用面向对象。但是这种方法的泛用性不够强，在建树的时候需要根据题目要求运用不同技巧。为了在各种考察树的题目中都能快速地建树，这里介绍一种基于面向对象的建树方法，叫作链表。

class Node(object):
    # 每个节点对象由一个变量 val 和一个列表 child 组成
    # val 存放节点的值, child 存放其子节点
    def __init__(self, val, child=[]):
        self.val = val
        self.child = child

# 构建根节点, 其值为1
root = Node(1)

# 将一个值为3的节点添加为 root 的一个子节点
root.child.append(Node(3))

# 再添加两个节点
root.child.append(Node(4))
a = root.child[0]
a.child.append(Node(2))

# 此时建立了一颗这样的树
#       1 (root)
#      / \
#     3   4
#    /
#   2

上面这种方法适用于子节点数不确定的情况 (N叉树)，对于二叉树，我们可以使用以下方法来实现

class Node(object):
    def __init__(self, val, child=[None, None]):
        self.val = val
        self.child = child

# 定义一个值为2的根节点, 它的左子树值为1, 右子树值为4
root = Node(2)
root.child[0] = Node(1)
root.child[1] = Node(4)

也可以这样实现

class Node(object):
    def __init__(self, val):
        self.val = val
        self.leftChild = None
        self.rightChild = None

# 定义一个值为1的根节点, 它的左子树值为3, 右子树值为5
root = Node(1)
root.leftChild = Node(3)
root.rightChild = Node(5)

【P1305 新二叉树 】https://www.luogu.com.cn/problem/P1305以上面这道题为例，我们在输入的时候就可用下面这段代码来构建树。但是，下面这段代码粗略看看即可，不需要学，因为有更简单的方法，那就是使用邻接表来建立树。

# 定义二叉树节点类
class Node(object):
    def __init__(self, val, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

# 使用字典辅助建树, 这种方式和后面要讲的邻接表很相似
# 在仅知道节点间关系的时候, 其实可以直接用邻接表来建树
# node[n] 表示根节点编号为 n 的树
node = {}
def getNode(n):
    global node
    # 根据题干, 星号表示空节点, 返回 None 即可
    if n == '*':
        return None
    # 如果之前没有建立过这个节点, 则先建立这个节点
    if n not in node:
        node[n] = Node(n)
    # 返回该节点
    return node[n]

n = int(input())
for i in range(n):
    n, left, right = map(str, input())
    # 如果之前没有建立过这个节点, 则先建立这个节点
    if n not in node:
        node[n] = Node(n)
    # 在该节点中添加子节点
    node[n].left, node[n].right = getNode(left), getNode(right)

看完是不是觉得代码量很大，感觉很麻烦。其实有一种建树方式，它可以大大减少代码量，那就是邻接表。为什么组长不一开始就介绍邻接表建树呢，因为这种方法基本只适用于做题，在实际工程中还是要用链表来建树的。一言蔽之，邻接表建树属于 “应试解法”，实际工程不建议使用。

接下来，还是基于上面这道题目，组长给出用邻接表建树的示范

n = int(input())
tree = {}
for i in range(n):
    node, left, right = map(str, input())
    tree[node] = [left, right]

是不是非常方便，代码量少得夸张。邻接表是 Python 实现图时所用到的方法，在下面讲解 “图” 的内容中会涉及邻接表，可以参照后续的【图的实现】来学习这个内容。

这一题也是一道理解树的递归性质的好题，请参照洛谷题解或其他资料完成此题，在学习了邻接表后，请尝试使用邻接表来构造这道题的树结构

图的实现 : 邻接矩阵、邻接表

照例，我们先了解一下图的概念及相关术语  【图的基本概念及相关术语】

python要实现图，有两种比较简单的方式，第一种即为邻接矩阵，使用一个二维矩阵，记录每个点之间的关系。下面为一小段示例

# 使用邻接矩阵表示以下有向图
#    0 --> 1 <--> 2
#    ^     |
#    |     |
#    3 <---+

Max = 2 ** 10
graph = [[0, 1, Max, Max],
         [Max, 0, 1, 1],
         [Max, 1, 0, Max],
         [1, Max, Max, 0]]
# 自身到自身的距离为 0
# 如果点x能到达点y, 则 graph[x][y] = 1
# 这是无权图的情况, 若有边权val, 则 graph[x][y] = val
# 当两点之间没有直接通路时,两点之间的距离视作无限大,这里用 Max 表示无限大

# 查询0号点到1号点的边, 结果为1, 说明有从0号点到1号点的边
print(graph[0][1])

# 查询1号点到0号点的边, 结果为Max, 说明没有从1号点到0号点的边
print(graph[1][0])

有时候节点的编号不一定是数字而是字符串，这时候可以用一个列表赋予每个节点一个数字编号

# 假设有一个图, 包含四个节点: a/b/c/d
#   a ---> c
#   ^
#   |
#   b <--> d
# 则可以用一个列表存放这四个节点
# 就可以使用对应节点在列表的索引来构造邻接矩阵

node = ['a', 'b', 'c', 'd']

# 这个图就可以表示为
#  0 ---> 2
#  ^
#  |
#  1 <--> 3

Max = 2 ** 10
graph = [[0, Max, 1, Max],
         [1, 0, Max, 1],
         [Max, Max, 0, Max],
         [Max, 1, Max, 0]]

还有一种方法叫作邻接表，可以使用列表来实现，也可以使用字典来实现，这里给出使用字典实现的示例

# 使用邻接矩阵表示以下有向图
#    0 --> 1 <--> 2
#    ^     |
#    |     |
#    3 <---+

graph_1 = { 0: [1],
            1: [2, 3],
            2: [1],
            3: [0],}

# 无权图 node1: [node2, node3, ...]
# 有权图 node1: [(val_a, node2), (val_b, node3), ...]

# 使用邻接矩阵表示以下有向有权图
#   a -1-> c
#   ^
#   |3
#   b <-2-> 4

graph_2 = { 'a': [(1,'c')],
            'b': [(3,'a'), (2,'4')],
            'c': [],
            '4': [(2,'b')],}

字典中每个 key 都表示一个节点，又对应一个列表，列表中存放着指向下一个节点的边；如果有边权的话，就使用一个集合 (val, node) 来表示边，val表示边权，node表示指向的节点。

大家还记不记得前面讲树时组长给出了一种使用邻接表建树的方法，这种方式这么好用，为啥我说这是 “应试方法” 呢？因为邻接表要求每个节点都有自己的编号，而实际工程中树中的节点一般是不会有编号的。然而，组长发现，许多考察树结构的算法题都会赋予每个节点一个编号，于是决定讲一下邻接表建树的方法，让大家解题更快更容易。

好了，说了这么多，是时候来点实战，下面给出一道例题，以及组长的示范代码（这道题用 python 会超时的，验证程序的时候过掉样例即可）

【B3613 图的存储与出边的排序】https://www.luogu.com.cn/problem/B3613

# 方法1 邻接表
ans = [] # 建立一个列表存放答案

t = int(input())
for i in range(t):
    n, m = map(int, input().split())
    graph = {} # 建立一个空的图
    # 添加 n 个节点
    for node in range(n):
        graph[node] = []
    # 添加 m 条边
    for j in range(m):
        u, v = map(int, input().split())
        graph[u - 1].append(v) # u -> v
    # 将每条边指向的节点编号做排序, 然后记录到 ans 中
    for j in range(n):
        ans.append(sorted(graph[j]))

# 输出结果
for i in ans:
    print(" ".join(list(map(str, i))))

# 方法2 邻接矩阵
ans = []  # 建立一个列表存放答案

t = int(input())
for i in range(t):
    n, m = map(int, input().split())
    # 建立一个空的图
    graph = []
    for j in range(n + 1):
        graph.append([0 for _ in range(n + 1)])
    # 向图里添加 m 条边
    for j in range(m):
        u, v = map(int, input().split())
        graph[u][v] = v # u -> v 
    # 将答案记录到 ans 中
    for node in range(1, n + 1):
        ans.append([])
        for next in graph[node]:
            if next:
                ans[-1].append(next)

# 输出结果
for i in ans:
    print(" ".join(list(map(str, i))))

接下来再给出几道练习题

【B3644 【模板】拓扑排序 / 家谱树】    【P1807 最长路 】    【P4017 最大食物链计数 】

d. 算法技巧指导

贪心法

在使用贪心法对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，这种算法得到的是在某种意义上的局部最优解。下面给出一道例题

【P2676 [USACO07DEC] Bookshelf B 】https://www.luogu.com.cn/problem/P2676

这道题非常简单地体现了贪心算法的“贪心”特点：既然要使用尽量少的奶牛，那每次在选择奶牛时，我们就选择最高的那只。那怎么知道哪只最高，就要用到排序，其实很多时候“贪心”和“排序”是一起出现的。下面是示范代码

cow = [] # 用一个列表存放奶牛身高数据

N, B = map(int, input().split()) # 输入奶牛数量和书架高度

# 输入 N 只奶牛的身高数据
for i in range(n):
    cow.append(int(input()))
# 对身高进行降序排列
cow.sort(reverse=True)

H = 0 # 初始高度为0
# 利用贪心法, 如果未达到高度, 则将下一只奶牛加入
for ans in range(len(cow)):
    H += cow[ans]
    if H >= B:
        break
print(ans + 1)

贪心法不难学会，难的是运用。作为一种技巧，它经常会隐蔽地出现在其它考点的题目中，这就需要大家多刷题，培养题感。下面给出一些练习

【P2240 【深基12.例1】部分背包问题 】    【P1803 凌乱的yyy / 线段覆盖 】    【P1843 奶牛晒衣服 】

请注意，不要滥用贪心法。要记住贪心法得到的往往是“局部最优解”，在一些需要整体考虑的情况下不适用，例如前面讲到的背包问题。

二分查找

在解题时，我们有时可以通过在数据范围内逐项枚举的方式，来求出答案。但是，如果数据范围很大，逐项枚举来求解就不现实了。这时可以运用搜索、dp之类的算法，有时也能使用二分查找来优化时间复杂度。

下面以一道例题来展示二分查找的过程

【P8647 [蓝桥杯 2017 省 AB] 分巧克力 】https://www.luogu.com.cn/problem/P8647

我们先使用一种朴素的思路来求解，那就是从 1 开始一直枚举到10 的五次方，逐次判断能否切出 K 块这个边长的巧克力，当判断到不能切出 K 块边长为 L 的巧克力时，输出答案 ans = L - 1 

# n块巧克力, k个小朋友
n, k = map(int, input().split())

# 使用列表存放巧克力的长和宽
H = []
W = []
for i in range(n):
    h, w = map(int, input().split())
    H.append(h)
    W.append(w)

# 判断能否切出 k 块边长为 L 的巧克力
def check(L):
    global n, k, H, W
    num = 0
    for i in range(n):
        hcut = H[i] // L
        wcut = W[i] // L
        num += hcut * wcut
    return num >= k

# 从 1 开始枚举, 直到找出答案
for L in range(1, 10**5 + 1):
    if not check(L):
        break
print(L - 1)

在如此大的数据范围下，这种方法毫不意外地超时了。这时我们可以使用二分查找来显著减少查找次数，只需要将最后的枚举过程改成以下代码

left, right = 0, 10**5
while left + 1 < right:
    mid = (left + right) // 2
    if check(mid):
        left = mid
    else:
        right = mid
print(left)

二分查找本身并不难写，套上面的模板即可，然后根据具体情况加以改动，例如改变 left 和 right 的初始值、将 left = mid 和 right = mid 换位

最重要的是 check 函数，能否构造出这个函数，基本决定了能否解出题目。而对于 check 函数的构建，很多时候会涉及到上面讲过的贪心法。要想顺利写出 check 函数，也需要不少的练习，这里给出两道练习题

【P1843 奶牛晒衣服】   【P1182 数列分段 Section II】

二进制枚举

请看以下情景：桌上有10个食物，它们的美味程度用列表 food 存储，我现在任意取出几个食物，请问有几种取法，使得取出食物的美味程度之和符合某种要求

food = [1, 2, 1, 4, 5, 3, 3, 8, 6, 2]

最无脑的方法是嵌套 10 个 for 循环来枚举所有情况，也可以使用 DFS 来搜索全部情况

这里有一种新的方法，叫作二进制枚举，它适用于物体状态只有两种的场合（这里物体只有被取出和没被取出两种状态） 我们利用二进制只包含0和1的特点，用一串二进制数来表示一种情况，以二进制数 1010011101 为例：

food	1	2	1	4	5	3	3	8	6	2
二进制数	1	0	1	0	0	1	1	1	0	1
是否取出	是	否	是	否	否	是	是	是	否	是

那么我们就只需要使用【10的十次方】以内的二进制数，即可表示所有情况，那么二进制中【10的十次方】转换为十进制是多少呢？是【2的十次方】即1024，也就是说，我只需要下面的一个 for 循环即可枚举所有情况

for i in range(1024):
    print(bin(i))
    # bin函数接收一个十进制数, 返回对应的二进制数
    # 返回值的格式是字符串, 且前面带有 '0b' 标识

# 也可以这样
for i in range(2**10):
    print(bin(i))

然后我们将得到的二进制数进行一些处理，即可逐位检查是 "0" 还是 "1"

# 输入物品个数
n = int(input())

for i in range(2**n):
    # 转换为二进制后利用切片将 '0b' 去掉
    # 然后用 zfill 方法补 0
    m = bin(i)[2:].zfill(n)
    print(m)
    for j in m:
        if j == '1':
            print("有", end="")
        else:
            print("无", end="")
    print('')

记忆化搜索

在使用搜索解题的过程中，有时候会搜索到曾经出现过的情况，这时候可以使用记忆化的技巧，记录已经解出的子问题的结果，来加速搜索的过程。下面是一道十分经典的考察记忆化的例题

【P1464 Function 】https://www.luogu.com.cn/problem/P1464不考虑时间复杂度，要写出题解其实很简单，递归即可

# 使用递归实现 w 函数
def w(a, b, c):
    if a <= 0 or b <= 0 or c <= 0:
        return 1
    if a > 20 or b > 20 or c > 20:
        return w(20, 20, 20)
    if a < b and b < c:
        return w(a,b,c-1) + w(a,b-1,c-1) - w(a,b-1,c)
    else:
        return w(a-1,b,c) + w(a-1,b-1,c) + w(a-1,b,c-1) - w(a-1,b-1,c-1)

ans = []
while True:
    a, b, c = map(int, input().split())
    if a != -1 or b != -1 or c != -1:
        ans.append("w({}, {}, {}) = {}".format(a, b, c, w(a,b,c)))
    else:
        break

# 输出答案
for i in ans:
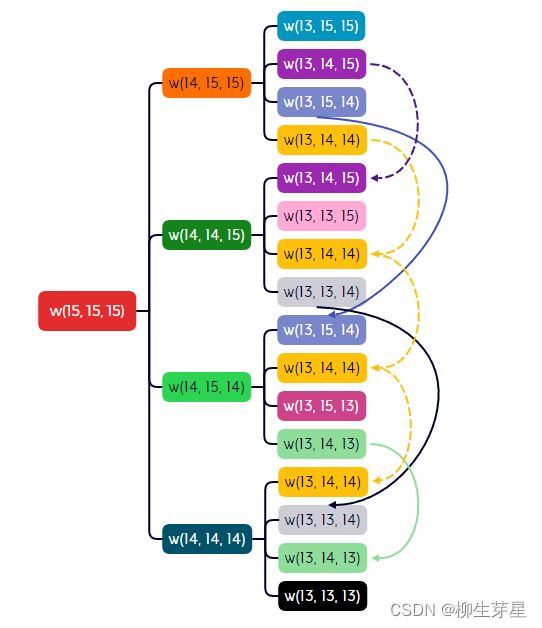
    print(i)

毫无疑问，超时！按照题干所给例子：w(15, 15, 15)，我们来推演一下递归过程：

可以看到，在递归深度为2时，就出现了大量重复的情况，像 w(13, 14, 14) 就重复出现了四次，如果我们能在第一次计算 w(13, 14, 14) 时就将结果存储起来，那后面的三次就可以直接使用存储的结果，而不需要做重复工作。

让如何实现记忆化呢？方法是使用一个三维列表 rem[a][b][c] 来存放 w(a, b, c) 的结果

# 建立一个 25x25x25 的三维列表
rem = []
for i in range(25):
    rem.append([])
    for j in range(25):
        rem[i].append([0 for _ in range(25)])

# 使用递归实现 w 函数
def w(a, b, c):
    global rem
    # 这两种情况直接返回即可
    if a <= 0 or b <= 0 or c <= 0:
        return 1
    elif a > 20 or b > 20 or c > 20:
        return w(20, 20, 20)
    # 如果是已经遇到的情况, 则直接返回记忆的结果
    elif rem[a][b][c] != 0:
        return rem[a][b][c]
    # 如果是尚未遇到的情况
    elif a < b and b < c:
        # 将结果记忆到 rem 中
        rem[a][b][c] = w(a,b,c-1) + w(a,b-1,c-1) - w(a,b-1,c)
        return rem[a][b][c]
    else:
        # 将结果记忆到 rem 中
        rem[a][b][c] = w(a-1,b,c) + w(a-1,b-1,c) + w(a-1,b,c-1) - w(a-1,b-1,c-1)
        return rem[a][b][c]

ans = []
while True:
    a, b, c = map(int, input().split())
    if a != -1 or b != -1 or c != -1:
        ans.append("w({}, {}, {}) = {}".format(a, b, c, w(a,b,c)))
    else:
        break

# 输出答案
for i in ans:
    print(i)

记忆化搜索是一个十分重要的技巧，蓝桥杯竞赛常被称作 “搜索杯”，主要是因为大部分题目可以使用搜素来暴力解题。而单纯的暴力搜素是极容易超时的，于是就需要记忆化来对搜素进行升级。掌握了记忆化搜索，能帮助你在赛场上用相对简单的逻辑获得更多的分数。

打表

Python 选手在刷题的过程中总会有一个尴尬，那就是受限于语言的性能，同样的逻辑下，Python 跑的时间总是比 C/C++ 等多很多，这就导致想出了正解，但还是因为超时而拿不到分数。

在题目数据范围比较小的情况下，可以考虑使用打表这个“歪门邪道”来避免超时的尴尬

什么是打表呢？就是将数据范围内所有情况的答案都跑出来，使用一个列表/字典存起来，然后我们只需要根据输入，对应输出列表/字典中的内容即可，这种方法是时间复杂度是惊人的O(1)

举个例子：

【P1219 [USACO1.5] 八皇后 Checker Challenge 】https://www.luogu.com.cn/problem/P1219这道题写出题解并不难，但是很容易超时。再看数据范围，输入的范围是 6<= n <=13，很小。在算法竞赛争分夺秒的场景下，与其花费很多时间来寻求时间复杂的优化，不如将 6<= n <=13 的结果跑出来，然后使用下面的代码来得分

n = int(input())
if n == 6:
    print("2 4 6 1 3 5\n3 6 2 5 1 4\n4 1 5 2 6 3\n4")
if n == 7:
    print("1 3 5 7 2 4 6\n1 4 7 3 6 2 5\n1 5 2 6 3 7 4\n40")
if n == 8:
    print("1 5 8 6 3 7 2 4\n1 6 8 3 7 4 2 5\n1 7 4 6 8 2 5 3\n92")
if n == 9:
    print("1 3 6 8 2 4 9 7 5\n1 3 7 2 8 5 9 4 6\n1 3 8 6 9 2 5 7 4\n352")
if n == 10:
    print("1 3 6 8 10 5 9 2 4 7\n1 3 6 9 7 10 4 2 5 8\n1 3 6 9 7 10 4 2 8 5\n724")
if n == 11:
    print("1 3 5 7 9 11 2 4 6 8 10\n1 3 6 9 2 8 11 4 7 5 10\n1 3 7 9 4 2 10 6 11 5 8\n2680")
if n == 12:
    print("1 3 5 8 10 12 6 11 2 7 9 4\n1 3 5 10 8 11 2 12 6 9 7 4\n1 3 5 10 8 11 2 12 7 9 4 6\n14200")
if n == 13:
    print("1 3 5 2 9 12 10 13 4 6 8 11 7\n1 3 5 7 9 11 13 2 4 6 8 10 12\n1 3 5 7 12 10 13 6 4 2 8 11 9\n73712")

打表不需要练习，在竞赛过程中，其实经常会写一些时间复杂度比较高的程序。有些时候（例如填空题）是不需要过分追求代码高效的，切忌在比赛现场钻牛角尖，导致后续做题时间不足。

下一篇 【VSCode 配置指南】