线性结构--栈与队列(Python实现)
一、 栈的原理
如果用列表构建栈,那么栈顶(top)对应着列表表尾,栈底(bottom)对应列表表头
栈只能在栈顶进行操作:入栈/进栈/压栈/push
出栈/pop
栈的性质:后进先出
二、 栈的Python方法实现
利用列表构建栈,可以使用python自带的入栈(lst.append)、出栈(lst.pop)函数,十分方便:
# 构建了一个长度无限的栈
class Stack:
def __init__(self):
self.stack = []
def push(self, element):
return self.stack.append(element)
def pop(self):
if self.is_empty():
raise IndexError("Stack is empty")
else:
return self.stack.pop()
def get_top(self):
if self.is_empty():
raise IndexError("Stack is empty")
else:
return self.stack[-1] # 输出表尾
def is_empty(self):
if len(self.stack) == 0:
return True # 是空栈
else:
return False
if __name__ == "__main__":
init_stack = Stack()
init_stack.stack = [1, 2, 3, 4, 5]
init_stack.push(6) # 进栈:6
init_stack.pop() # 出栈:6
for items in init_stack.stack:
print(items) # 栈的遍历
三、栈的实际应用--括号匹配问题
利用栈“后入先出”的性质,处理对称的字符串或进行深度优先搜索,将十分方便:
from stack import Stack
# 遇到左半部分括号,进栈;
# 遇到右半部分括号,根据字典进行比对:比对成功,左半部分括号出栈;比对错误,结束匹配
def kuo_hao(the_list):
stack = Stack() # 空列表 stack.stack 以及待检测字符串 the_list
pi_pei = {'}': '{', ']': '[', ')': '('} # 构建一个字典
for item in the_list: # 遍历字符串
if item in {'{', '[', '('}: # 如果元素在集合里面
stack.push(item)
else:
if stack.is_empty():
return False # 右括号找不到对应的左括号
elif pi_pei[item] == stack.get_top():
stack.pop()
else:
return False # 右括号不匹配对应的左括号
if stack.is_empty():
return True
else:
return False
if __name__ == '__main__':
print(kuo_hao('[{()}]')) # 输入字符串
print(kuo_hao('[{)}'))四、栈的实际应用--算式判别问题
具体原理详见https://blog.csdn.net/Amentos/article/details/127182926
简单易上手的python实现详见https://blog.csdn.net/jackandsnow/article/details/100525460
在此基础上,本人实现了多位数、带括号、带小数的中缀表达式转后缀表达式并求值,最终呈现结果为读取txt文件中的等式,进行计算结果与等式中结果的比较。计算结果等于等式结果但形式不符(0与0.0)、计算结果等于等式结果且形式相符、计算结果不等于等式结果均会提示。
from decimal import Decimal
def generate_postfix(infix): # 本函数实现了中缀表达式转后缀表达式
"""
generate postfix expression str
:param infix: infix expression str, like '2×3+8÷3'
:return: postfix expression str, like '23×83÷+'
"""
op_rank = {'×': 2, '÷': 2, '+': 1, '-': 1, '(': 0} # 定义加减乘除括号的优先级
stack = [] # 用list模拟栈的后进先出
post_list = [] # 输出的后缀表达式
num = ''
for index, s in enumerate(infix):
if s == '(': # 左括号,直接进栈
stack.append(s)
elif s == ')': # 右括号,将左括号及之后全部出栈
while stack[-1] != '(':
post_list.append(stack.pop())
stack.pop()
elif s in '+-×÷':
# 栈不为空,且栈顶运算符的优先级高于当前运算符,一直退栈到循环终止
while stack and op_rank.get(stack[-1]) >= op_rank.get(s):
post_list.append(stack.pop())
stack.append(s)
else: # 是数字,直接进后缀表达式
if index < len(infix) - 1 and infix[index + 1] in '1234567890.': # 如果下一位是数字或未遍历完
num = num + s
else:
post_list.append(num + s)
num = '' # 如果下一位不是数字或已经遍历完了,则将合成的数字作为一个元素存进列表中,中间变量清空
while stack: # 中缀表达式遍历完了,stack所有元素出栈
post_list.append(stack.pop())
return post_list
def calculate_postfix(postfix): # 本函数实现了后缀表达式的求值运算
"""
calculate postfix expression
:param postfix: postfix expression str, like '23×83÷+'
:return: int result, like 2×3+8÷3=6+2=8
"""
stack = [] # 用list模拟栈的后进先出
for p in postfix:
if p in '+-×÷':
value_2 = float(stack.pop()) # 第二个操作数
value_1 = float(stack.pop()) # 第一个操作数
if p == '+':
result = round(value_1 + value_2, 3)
elif p == '-':
result = round(value_1 - value_2, 3)
elif p == '×':
result = round(value_1 * value_2, 3)
else: # 整除
result = round(value_1 / value_2, 3)
stack.append(result)
else:
stack.append(p)
return stack.pop()
if __name__ == "__main__":
file_deal = './eval.txt'
equation = open(file_deal, 'r', encoding='utf-8').readlines()
for item in equation: # 遍历列表中每个元素
item1 = item[0: item.index('=')] # 得到算式
item2 = item[item.index('=') + 1: item.index('\n')]
result1 = generate_postfix(item1) # 得到后缀表达式
print(item[0: item.index('\n')], end=" ")
result2 = calculate_postfix(result1) # 得到计算结果,会给无小数的结果补0
# print('item={} Decimal_result={}'.format(item2, result2), end=" ")
# 如果无小数,进行去0操作
if int(result2) == result2:
if Decimal(result2) == Decimal(result2).to_integral():
result2 = Decimal(result2).to_integral()
else:
result2 = Decimal(result2).normalize() # 计算结果舍弃小数点后多余的0
# 计算结果与原结果比较
if float(item2) == result2 and item2 != str(result2): # 0.0与0的数值相同但是形式错误
print("True,but formal error")
elif float(item2) == result2 and item2 == str(result2):
print("True")
else:
print("False")
已将代码及txt文件上传至github:https://github.com/dukousansan/-.git
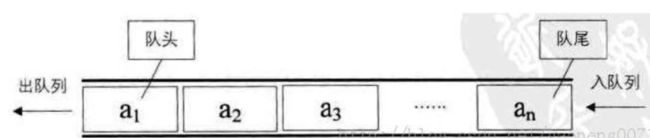
五、队列原理
如果用列表实现队列,那么列表表头相当于队列的对头,列表表尾相当于队列的队尾
根据不同的需要,可以构建“单向队列”、“循环队列”、“双向队列”等
队列的性质:先进先出
六、队列的python方法实现:
建议利用collections库实现队列,这是一个双向队列,有表头进队、表头出队、表尾进队、表尾出队功能:
# deque是一个双向队列,可以实现队首队尾出队、队首队尾入队
from collections import deque
def in_de_queue():
queue = deque([1, 2, 3]) # 实例化,创建对象queue
queue.pop() # 队尾出队(3)
queue.append(4) # 队尾入队(4)
queue.appendleft([7, 8, 9]) # 队首入队([7,8,9])
queue.appendleft(6) # 队首入队(6)
queue.popleft() # 队首出队(6)
print(queue)
def read_txt(lines):
with open("test.txt", 'r') as f:
q = deque(f, lines) # 得到txt文件中后lines列,每一列为一个元素
for items in q:
print(items, end='') # end=''就不会多一行空格
if __name__ == "__main__":
in_de_queue()
print("---------")
read_txt(5)