Proof Compression

1. 引言

借助zk-SNARKs的灵活性，可让DeFi隐私交易更便宜更简单。

Aztec团队致力于让通用零知识交易尽可能简单的同时，对zk密码学进行大幅改进，使这些交易简单的同时还足够便宜。

2. 设计证明系统的取舍

在零知识证明系统中，Prover致力于让Verifier信服某statement是正确的，同时Prover给Verifier分享的statement信息尽可能少。
零知识证明系统主要分为2个阶段：

• 1）证明生成阶段
• 2）证明验证阶段

理想情况下，这2个阶段应都足够快且计算高效，但是，现实情况是通常需要在二者之间进行取舍权衡。从计算角度来说，构建证明的计算量要远大于验证证明的计算量，当提到某“fast” 构建证明算法时，“fast”是相对于某基准线，而不是相对于verification的。

在Aztec的zk-rollup中，有3个不同的角色参与创建和验证SNARK proofs，每个角色具有不同的计算能力和限制：

• 1）用户：用户拥有秘密信息，如其balance，其历史交易。用户想在保持隐私的情况下，参与交易，并与DeFi协议交互。用户可在web浏览器中生成证明，浏览器通常运行在低计算能力的设备，如手机上。
• 2）Rollup Provider：rollup provider负责将用户交易进行打包和压缩，该流程中包含了生成proof和验证proof（具体看下面的recursion讨论）。rollup provider通常可访问商用级别硬件。
• 3）区块链：Ethereum Virtual Machine（EVM）为计算高度受限的环境，EVM中的每个运算有所不同，但通常都是昂贵的，相应的开销必须由用户以交易手续费支付。EVM负责验证一个proof（其中可能包含了多个其它proof）。

为了给Aztec的用户带来实惠的、真正的零知识交易，我们跨递归边界将不同的证明系统（特别是PlonK的不同、美味口味）融合在一起。对于用户来说，这意味着在客户端证明生成期间降低了计算成本，同时通过最小化EVM上的计算降低了货币成本。

3. Recursion

由于验证某proof $p$本身也是某种计算，因此可引入另一个零知识证明$p^{\ast }$来证实“验证某proof $p$ 成功”，从而实现递归证明。同时$p^{\ast }$本身也必须被验证。
接下来看如何将2个不同的证明系统进行结合或组合？

将证明系统看成是$(\mathbf{P},\mathbf{V})$算法组，存在2个参与者Prover和Verifier。
假设：

• 存在某证明系统$(\mathbf{P},\mathbf{V})$，其构建proof cheap，但验证proof昂贵；（如TurboPlonK）
• 存在另一证明系统$({\mathbf{P}}^{\ast },{\mathbf{V}}^{\ast })$，其构建proof 昂贵，但验证proof cheap；（如PlonK）

需对以上2种证明系统进行组合，以使利益最大化：

• 1）采用证明系统$\mathbf{P}$来构建proof $\pi$；
• 2）基于证明系统${\mathbf{P}}^{\ast }$来构建proof ${\pi }^{\ast }$，其中${\pi }^{\ast }$为a proof that attests to the correct verification of $\pi$ under $\mathbf{V}$；
• 3）验证${\pi }^{\ast }$。

最终可由具有不同计算能力的参与者来执行以上3个步骤。正是这种思想，使得Aztec Connect可为用户提供便宜隐私的交易。
以Plonk和TurboPlonk这2种证明系统组合使用为例：

• 1）Client：使用TurboPlonk来构建proof $\pi \text{-Client}$。TurboPlonk为Plonk的变种，支持定制门，从而可在计算能力受限的设备上高效构建生成proof。
  Client将$\pi \text{-Client}$发送给Rollup Provider。
• 2）Rollup Provider：以$\pi \text{-Client}$为输入，构建Standard（即non-Turbo）Plonk proof $\pi \text{-Rollup}$，以证明$\pi \text{-Client}$被正确验证。因此，Rollup Provider受限于TurboPlonk高昂的验证开销，以及，Standard Plonk proof构建开销。但rollup provider是强大的，其可解决TurboPlonk验证和Standard Plonk生成证明开销，以及为用户节约开支的同时，仍能获利。proof $\pi \text{-Rollup}$会发送到以太坊。
• 3）通过部署在以太坊链上的StandardVerifier.sol合约，可验证$\pi \text{-Rollup}$。

注意：为了进一步优化压缩流程，Aztec rollup provider实际包含了3步recursion：

• 2步 Turbo->Turbo递归（使用rollup circuits和root rollup circuits，详细组装解释见Privacy for Pennies: Scaling Aztec’s zkRollup）
• 1步 Turbo->Standard递归（使用root verifier circuit）

4. Nerds插曲：定制门

假设你为协议制定者，要求所设计的零知识证明系统可证明包含了类似$a+b=c,(a+b)\cdot c=d,a\cdot b\cdot c=d$等加法和乘法组合的statement，但你的证明系统中仅包含一类gate，形如：
$q_{mult}\times (w_l{w}_r)+(1-q_{mult})\times (w_l+w_r)-w_o=0$【待证明的identity degree为3】
其中$w$表示“wires” with $l=left,r=right,o=output$，$q$为"selector"用于在乘法和加法之间切换。

当要证明存在数字$a,b,c,d$满足$(a+b)\times c=d$时，相应的电路设计模板为：

相应的电路类似为：

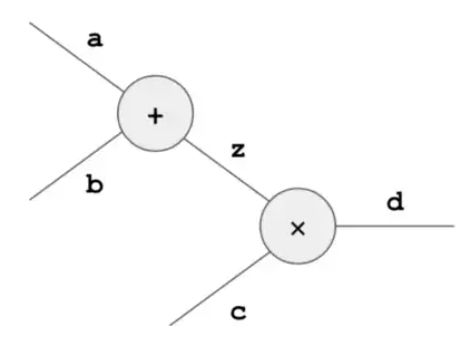
将$a,b,c,d,z$值填入电路设计模板中：

用户可证明相应的值满足该claim。（此处，必须在2个$z$之间进行约束，即使用copy constraints。）

当用户还想要证明形如$x^5=y$这样的statements时（如Poseidon hash中包含了这样fifth powers计算），若采用上面的思路，需将其分解为一系列乘法和一个加法：
$x^5-y=[((x\times x)\times (x\times x))\times x]-y=0$

将相应的值填入模板，获得execution trace形如：

不同于以上方案，可引入新的custom selector，形如：
$q_{custom}\times w_l^5+(1-q_{custom})\times (q_{mult}\times (w_l{w}_r)+(1-q_{mult})\times (w_l+w_r))-w_o=0$【待证明的identity degree为6】

此时$x^5=y$的电路仅需要一个gate，形如：

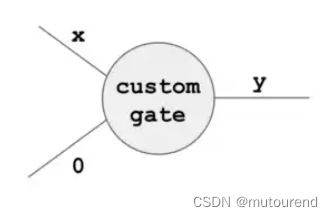
相应的execution trace为：

通过引入定制门，将整个电路由6个门减少到了3个门，从而减少了50% 的circuit size。

不过，引入定制门将增加待证明的identity degree，从而意味着增加Prover的计算量，可能会抵消掉部分circuit size reduction的好处。如上例引入定制门后，待证明的identity degree由3变成了6，而circuit size减半了（由6变成了3）。若程序中仅包含少量这样的定制门计算，则需要重新考虑引入定制门的意义，实际上，需要考虑这种情况。

同时，另一个思路是：构建不会增加identity degree的定制门，或者不会增加prover太多计算量的定制门。详细将TurboPlonk证明系统，其关键创新在于在计算Pedersen哈希时，引入了充分利用椭圆曲线高效scalar multiplication计算的定制门。

5. Prover和Verifier开销

在证明系统设计时：

• 1）Prover复杂度与circuit中的gates数紧密关联；
• 2）Verifier复杂度与circuit size相对无关，但会随着待证明claim或identity的复杂度的增加而增加。

仍以上例为例，引入定制门后，有circuit size减少，相应的proof构建将更便宜；而Verifier的验证将相对昂贵，因其无法受益于circuit size 减少，而同时必须面对引入定制门后identity复杂度的增加。

对于Prover和Verifier来说，大量的计算开销在于需计算昂贵的椭圆曲线scalar multiplication。
对于Verifier来说，在identity中引入额外的selector意味着在验证时需增加额外的scalar multiplication运算。
以Standard Plonk中Verifier的第9步计算为例：

其中$q$ 为selector，$\cdot$表示scalar multiplication。更多的selector，该公式将更复杂。

6. 展望

Aztec将TurboPlonk进一步升级为UltraPlonk，UltraPlonk为TurboPlonk+Plookup：

• 使用lookup tables来进步加速proof构建，代价是增加Verifier开销。

同时，Aztec还设计了名为fflonk协议：

• proof验证效率高，代价是prover开销大。

fflonk为SHPlonk承诺机制的变种，具有潜力可降低约35%的EVM执行开销。

参考资料

[1] Aztec团队2022年9月博客 Proof Compression