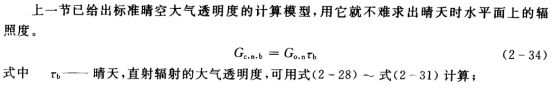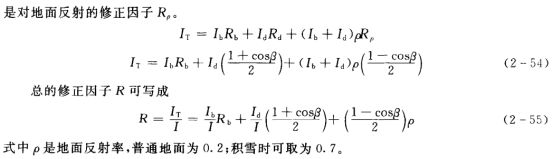计算某地的从日出到日落各时刻的水平面直射和散射辐射，倾斜面总辐射的Python程序

基本概念

大气质量

大气透明度τ

直射辐射透明度τ_b，散射辐射透明度τ_d。





晴空垂直直射辐射G_cnb

G_on是一年中第n天的地球外太阳辐射（a式简单，b式更精确）(大气层外法向的辐照度)

from sympy import *
month = 8
day = 22
#n()是一年里的第几天
def n():
    d_num = 0
    for m in range(1, month):
        if m in [1, 3, 5, 7, 8, 10, 12]:
            d_num += 31
        elif m in [2]:
            d_num += 28
        else:
            d_num += 30
    d_num += day
    return d_num
#日子数
n = n()
#计算大气层外法向的辐照度
G_sc = 1367  #单位W/m2
G_on1 = (G_sc * (1+0.033*cos(360*n/365*pi/180))).evalf()
B = (n-1)*360/365
G_on2 = (G_sc * (1.000110+0.034221*cos(B*pi/180)+0.001280*sin(B*pi/180)+0.000719*cos(2*B*pi/180)+0.000077*sin(2*B*pi/180))).evalf()
print(G_on1)
print(G_on2)

结果：

1338.48518301793
1335.56388385576

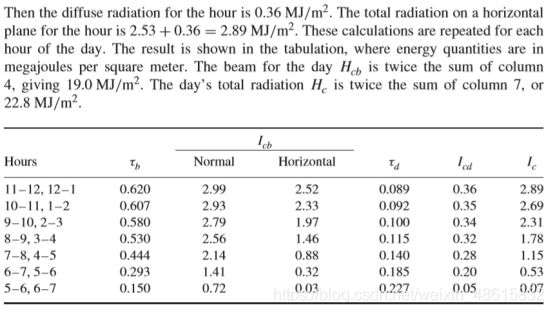
晴空水平直射辐射G_cb
对于一小时时间段内，晴空水平直射辐射I_cb

Tropical —— 热带，0°—30°南北纬
Midlatitude summer —— 中纬度夏季，30°—60°南北纬
Subarctic summer —— 高纬度夏季，60°—90°南北纬
Midlatitude winter —— 中纬度冬季，30°—60°南北纬

晴空，垂直于辐射方向上的太阳辐射照度G_cnb

水平面上的直射辐照度G_cb

一小时内，水平面上直射辐照量I_cb

水平面上的散射辐照度G_cd

一小时内，水平面上散射辐照量I_cd

一小时内，水平面上的总辐照量I_c

大气层外水平面上的太阳辐射照度G₀，W/m2

G_sc = 1367  #单位W/m2
G0 = G_sc * (1+0.033*cos(360*n/365*pi/180)) * cos(Theta_z*pi/180)

大气层外水平面上，1天内太阳的辐照量H₀，J/m2

from sympy import *
G_sc = 1367  #单位W/m2
H0 = 24*3600*G_sc/pi * (1+0.033*cos(360*n/365*pi/180)) * (2*pi*Omega_set/360*sin(Delta*pi/180)*sin(Phi*pi/180) + cos(Delta*pi/180)*cos(Phi*pi/180)*cos(Omega_set*pi/180))

大气层外水平面上，每小时内太阳的辐照量I₀，J/m2

from sympy import *
G_sc = 1367  #单位W/m2
I0 = 12*3600*G_sc/pi * (1+0.033*cos(360*n/365*pi/180)) * (2*pi*(Omega_2-Omega_1)/360*sin(Delta*pi/180)*sin(Phi*pi/180) + cos(Delta*pi/180)*cos(Phi*pi/180)*(sin(Omega_2*pi/180)-sin(Omega_1*pi/180)))

晴空指数K_T

小时散射辐射量I_d与小时总的辐射量I之比，与kT的关系

from sympy import *
I = 1    #小时的日辐照量
I0 = 2    #同小时大气层外日辐照量
kT = I/I0    #小时晴空指数
Id_I = None    #Id/I
if kT <= 0.22:
    Id_I  = 1 - 0.09*kT
elif kT <= 0.8:
    Id_I = 0.9511 - 0.1604*kT + 4.388*kT**2 - 16.638*kT**3 + 12.336*kT**4
else:
    Id_I = 0.165

或者可以采用下面的式子，这两个式子的结果都差不多，但前者中心部分精确，后者计算简单。

from sympy import *
I = 1    #小时的日辐照量
I0 = 2    #同小时大气层外日辐照量
kT = I/I0    #日晴空指数
Id_I = None    #Id/I
if kT <= 0.35:
    Id_I  = 1 - 0.249*kT
elif kT <= 0.75:
    Id_I = 1.557 - 1.84*kT 
else:
    Id_I = 0.177

小时散射辐射量I_d与小时总的辐射量I之比，与k_Tc的关系

I = 1    #小时的日辐照量
I_c = 2    #同小时标准晴空条件下大气层外日辐照量
kTc = I/I_c    #日标准晴空指数
Id_I = None    #Id/I
if kTc < 0.48:
    Id_I  = 1 - 0.1*kTc
elif kTc < 1.10:
    Id_I = 1.11 + 0.0396*kTc - 0.789*kTc**2
else:
    Id_I = 0.20

日散射辐射量H_d与日总的辐射量H之比，与KT的关系

from sympy import *
H = 1    #某天的日辐照量
H0 = 2    #同一天大气层外日辐照量
KT = H/H0    #日晴空指数
Hd_H = None    #Hd/H
if KT <= 0.17:
    Hd_H  = 0.99
elif KT < 0.75:
    Hd_H = 1.188 - 2.272*KT + 9.473*KT**2 - 21.865*KT**3 + 14.648*KT**4
elif KT < 0.8:
    Hd_H = -0.54*KT + 0.632
else:
    Hd_H = 0.2

小时总辐射量I与全天总辐射量（月平均每日水平辐射量）之比r_t

I = Ib + Id （小时总辐射量 = 小时直射辐射量 + 小时散射辐射量）

from sympy import *
a = 0.409 + 0.5016*sin((Omega_set-60)*pi/180)
b = 0.6609 - 0.4767*sin((Omega_set-60)*pi/180)
rt = pi/24 * (a+b*cos(Omega*pi/180)) * (cos(Omega*pi/180)-cos(Omega_set*pi/180))/(sin(Omega_set*pi/180)-(2*pi*Omega_set/360)*cos(Omega_set*pi/180))

小时散射辐射量与全天散射辐射之比r_d

from sympy import *
rd = pi/24 * (cos(Omega*pi/180)-cos(Omega_set*pi/180))/(sin(Omega_set*pi/180)-(2*pi*Omega_set/360)*cos(Omega_set*pi/180))

倾斜面和水平面上接受到的直射辐照量之比R_b

Beta = 20    #表面倾角
Theta = 60    #入射角
Theta_z = 70    #天顶角
Rb = (cos(Theta*pi/180)/cos(Theta_z*pi/180)).evalf()

表面上的总入射辐射I_T

有必要知道或能够估计太阳辐射入射到倾斜表面，如太阳能集热器、窗户或其他被动系统接收器上。入射太阳辐射是一组辐射流的总和，包括直射辐射、天空散射辐射的三个组成部分，以及倾斜表面“看到”的各个表面反射的辐射。这个表面上的总入射辐射可以写成


Liu和Jordan（1963）对此模型进行了改进，即各向同性扩散模型。倾斜表面上的辐射包括三个部分：光束、各向同性漫反射和地面漫反射太阳辐射。方程2.14.3中的第三项和第四项为零，因为所有漫射辐射均假定为各向同性。以坡度β从水平面倾斜的表面具有到天空的视角系数Fc−s=（1+cosβ）/2。（如果漫射辐射是各向同性的，这也是Rd，即倾斜表面上的漫射与水平表面上的漫射之比。）倾斜表面对地面的视角系数Fc−g=（1−cosβ）/2，如果周围环境对总太阳辐射的漫反射系数为ρg，则来自周围环境的反射辐射表面应为Iρg（1−cosβ）/2。因此，对方程2.14.3进行了修改，以给出倾斜表面上一小时的总太阳辐射为三项之和：

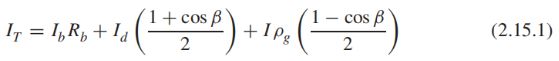
from sympy import *
Ib = 1    #小时水平面的直射辐射量 J/m2
Id = 1    #小时水平面的散射辐射量 J/m2
I = Ib + Id    #小时水平面的总辐射
Beta = 20    #表面倾角
Theta = 60    #入射角
Theta_z = 70    #天顶角
Rb = (cos(Theta*pi/180)/cos(Theta_z*pi/180)).evalf()
Rho_g = 0.2    #地面反射率ρg
#倾斜表面上一个小时的总的太阳辐射量I_T，J/m2
I_T = (Ib*Rb + Id*(1+cos((Beta*pi/180)/2))/2 + I*Rho_g*(1-cos((Beta*pi/180)/2))/2).evalf()

倾斜表面上的总辐射I_T与水平表面上的总辐射I之比R

当I_T被确定时，倾斜表面上的总辐射与水平表面上的总辐射之比可以被确定。根据定义，

根据式子（2.15.1），R=I_T/I可转化为

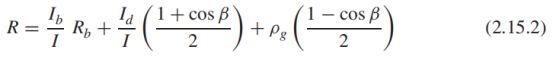
from sympy import *
Ib = 1    #小时水平面的直射辐射量 J/m2
Id = 1    #小时水平面的散射辐射量 J/m2
I = Ib + Id    #小时水平面的总辐射
Beta = 20    #表面倾角
Theta = 60    #入射角
Theta_z = 70    #天顶角
Rb = (cos(Theta*pi/180)/cos(Theta_z*pi/180)).evalf()
Rho_g = 0.2    #地面反射率ρg
#倾斜表面上一个小时的总的太阳辐射量I_T，J/m2
I_T = (Ib*Rb + Id*(1+cos((Beta*pi/180)/2))/2 + I*Rho_g*(1-cos((Beta*pi/180)/2))/2).evalf()
#总的修正因子
R = I_T/I

求水平面直射与散射的例题

英文版

中文版

代码

#求晴空条件下水平面的小时总辐照量Ic
#若求11:00-12:00的晴天辐照量，用中点11:30来代表。用类似方法对日照时间内每个小时进行详细计算
#麦迪逊，北纬43°，海拔高度270m，8月22日，太阳时11:30AM
from sympy import *
x = symbols('x')
month = 8
day = 22
hour = 11.5    #太阳时为11:30AM
Phi = 43    #纬度φ为43°
A = 0.27    #海拔高度，单位是km
#由于是水平面，所以平面倾角β=0
Beta = 0
#无特别指出，表面方位角为0
Gamma = 0

#n()是一年里的第几天
def n():
    d_num = 0
    for m in range(1, month):
        if m in [1, 3, 5, 7, 8, 10, 12]:
            d_num += 31
        elif m in [2]:
            d_num += 28
        else:
            d_num += 30
    d_num += day
    return d_num
def angle(Theta,Delta,Phi,Beta,Gamma,Omega):
    angle = cos(Theta*pi/180) - sin(Delta*pi/180)*sin(Phi*pi/180)*cos(Beta*pi/180) + sin(Delta*pi/180)*cos(Phi*pi/180)*sin(Beta*pi/180)*cos(Gamma*pi/180)\
            - cos(Delta*pi/180)*cos(Phi*pi/180)*cos(Beta*pi/180)*cos(Omega*pi/180) - cos(Delta*pi/180)*sin(Phi*pi/180)*sin(Beta*pi/180)*cos(Gamma*pi/180)*cos(Omega*pi/180)\
            - cos(Delta*pi/180)*sin(Beta*pi/180)*sin(Gamma*pi/180)*sin(Omega*pi/180)
    return angle

#弦截法迭代求根
def Secant_Method(fx,a,b):
    x0 = a  # 区间下限
    x1 = b  # 区间上限
    x_list = [x1]
    i = 0

    def f(xn):
        f = fx.subs(x,xn)
        return f.evalf()

    while True:
        x2 = x1 - f(x1) * (x1 - x0) / (f(x1) - f(x0))
        x0 = x1
        x1 = x2
        x_list.append(x2.round(1))
        if len(x_list) > 1:
            i += 1
            error = abs((x_list[-1