LeetCode通关:连刷十四题,回溯算法完全攻略
这一节,我们来看看回溯算法。
回溯算法理论基础
什么是回溯
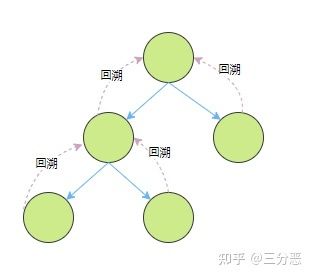
在二叉树的路径问题里,其实我们已经接触到了回溯这种算法。
例如我们在查找二叉树所有路径的时候,查找完一个路径之后,还需要回退,接着找下一个路径。
回溯其实可以说是我们熟悉的DFS,本质上是一种暴力穷举算法,把所有的可能都列举出来,所以回溯并不高效。
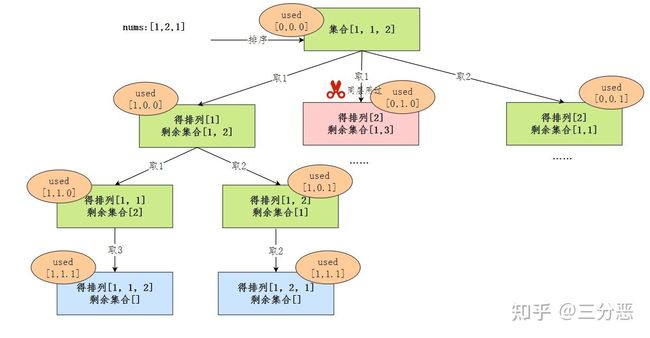
这个可能比较抽象,我们举一个例子吧,[1,2,3]三个数可以构成多少种组合呢?
我们的办法就是把所有结果都穷举出来,那怎么穷举呢?可以第一位选1,第二位从[2,3]里选2,第三位从[3]里选3;第二个组合可以第一位选2……
我们把这个选择抽象成一棵树,初步有个印象,这是全排列的问题,后面会刷到。
回溯算法模板
回溯算法,可以看作一个树的遍历过程,建议可以去看一下N叉树的遍历,和这个非常类似。
递归有三要素,类似的,回溯同样需要关注三要素:
- 返回值和参数
回溯算法中函数返回值一般为void。
回溯方法的参数得结合实际问题,但是一般需要一个类似栈的结构来存储每个路径(结果),因为我们一次递归结束之后,节点要回溯到上一个位置。
回溯方法伪代码如下:
void backtrack(参数)
- 回溯函数终止条件
和递归一样,回溯同样也要有结束条件。
什么时候达到了终止条件,从树的角度来讲,一般来说搜到叶子节点了,对回溯而言,就是找到了满足条件的一个结果。
所以回溯函数终止条件伪代码如下:
if (终止条件) {
存放结果;
return;
}
- 回溯搜索的遍历过程
回溯法一般是在一个序列里做选择,序列的大小构成了树的宽度,递归的深度构成的树的深度。
回溯函数遍历过程伪代码如下:
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
for循环就是遍历序列,可以理解一个节点有多少个孩子,这个for循环就执行多少次。可以理解为横向的遍历。
backtrack就是自己调用自己,可以理解为纵向的遍历。
同时递归之后,我们还要撤销之前做的选择。
所以回溯算法模板框架如下:
void backtrack(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtrack(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
回溯能解决哪些问题
回溯法,一般可以解决如下几种问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
可能到这对回溯还比较迷茫,没有关系,回溯是比较套路化的一种算法,多做几道题就明白了。
组合问题
LeetCode77. 组合
☕ 题目:77. 组合
❓ 难度:中等
描述:
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
示例 2:
输入:n = 1, k = 1
输出:[[1]]
思路:
这道题是回溯算法的经典题目。
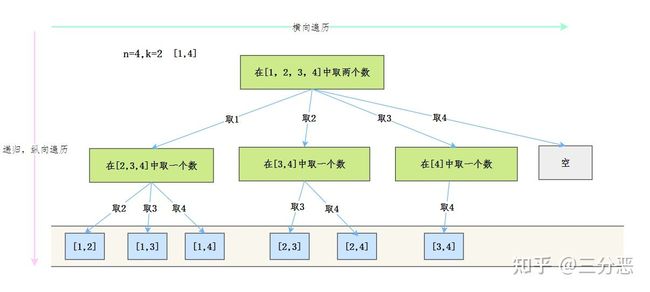
我们来看一下这道题的抽象树形结构:
按照我们的回溯模板,看看这道题应该怎么写:
- 返回值、参数
首先方法里是一定要区间的数据,[start,n]。
计数的k也不可缺少。
最后的结果集合result,还有每条路径的结果path,可以定义全局变量,来提升可读性。
- 终止条件
什么时候终止,就是什么时候到叶子节点了呢?结果parh的大小等于k,说明到了叶子节点,一次递归结束。
- 单层逻辑
在单层逻辑里面,我们要做两件事:
- 遍历序列
- 递归,遍历节点
代码:
class Solution {
//结果集合
List> result;
//符合条件的结果
LinkedList path;
public List> combine(int n, int k) {
result = new ArrayList<>();
path = new LinkedList<>();
backstack(n, k, 1);
return result;
}
//回溯
public void backstack(int n, int k, int start) {
//结束条件
if (path.size() == k) {
result.add(new LinkedList<>(path));
return;
}
for (int i = start; i <= n; i++) {
path.addLast(i);
//递归
backstack(n, k, i + 1);
//回溯,撤销已经处理的节点
path.removeLast();
}
}
}
⚡ 剪枝优化
回溯中,提高性能的一大妙招就是剪枝。
剪枝见名知义,就是在把我们的树的一些树枝给它剪掉。
例如n = 4,k = 4,
我们可以看到,有些路径,其实一定是不满足我们的要求,如果我们把这些不可能的路径剪断,那我们不就可以少遍历一些节点吗?
所以我们看看这道题怎么来剪这个枝:
如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了,那么就没有必要搜索。
- 已经选择的元素个数:path.size();
- 还需要的元素个数为: k - path.size();
- 所以起始位置 : n - (k - path.size()) + 1之后的肯定不符合要求
所以优化之后的代码如下:
class Solution{
//结果集合
List> result;
//符合条件的结果
LinkedList path;
public List> combine(int n, int k) {
result = new ArrayList<>();
path = new LinkedList<>();
backstack(n, k, 1);
return result;
}
//回溯
public void backstack(int n, int k, int start) {
//结束条件
if (path.size() == k) {
result.add(new LinkedList<>(path));
return;
}
for (int i = start; i <= n-(k-path.size())+1; i++) {
path.addLast(i);
//递归
backstack(n, k, i + 1);
//回溯,撤销已经处理的节点
path.removeLast();
}
}
}
LeetCode216. 组合总和 III
☕ 题目:77. 组合
❓ 难度:中等
描述:
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:
- 所有数字都是正整数。
- 解集不能包含重复的组合。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
思路:
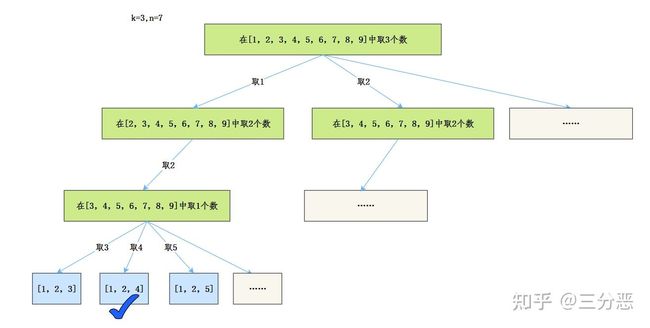
我们先把这道题抽象成树:
接着套模板。
- 终止条件
到叶子节点(path大小等于k)终止。
- 返回值,参数
参数稍微有变化,序列是固定的,这里的n是目标和;需要一个参数pathSum来记录路径上的数总和,我们直接全局变量。
- 单层逻辑
逻辑差别不大,回溯的时候需要把pathSum也回溯一下。
代码:
class Solution {
//结果集合
List> result;
//结果
LinkedList path;
//结果综合
int pathSum;
public List> combinationSum3(int k, int n) {
result = new ArrayList<>();
path = new LinkedList<>();
backtrack(n, k, 1);
return result;
}
//回溯
public void backtrack(int n, int k, int start) {
//结束
if (path.size() == k) {
if (pathSum == n) {
result.add(new LinkedList<>(path));
}
return;
}
//遍历序列
for (int i = start; i <= 9; i++) {
path.push(i);
pathSum += i;
//递归
backtrack(n, k, i + 1);
//回溯,撤销操作
pathSum -= path.pop();
}
}
}
⚡ 剪枝优化
同样也可以进行剪枝优化,也很好想,如果pathNum>n ,那就没必要再遍历了。
class Solution {
//结果集合
List> result;
//结果
LinkedList path;
//结果综合
int pathSum;
public List> combinationSum3(int k, int n) {
result = new ArrayList<>();
path = new LinkedList<>();
backtrack(n, k, 1);
return result;
}
//回溯
public void backtrack(int n, int k, int start) {
//剪枝优化
if (pathSum > n) {
return;
}
//结束
if (path.size() == k) {
if (pathSum == n) {
result.add(new LinkedList<>(path));
}
return;
}
//遍历序列
for (int i = start; i <= 9; i++) {
path.push(i);
pathSum += i;
//递归
backtrack(n, k, i + 1);
//回溯,撤销操作
pathSum -= path.pop();
}
}
}
LeetCode39. 组合总和
☕ 题目:39. 组合总和
❓ 难度:中等
描述:
给定一个无重复元素的正整数数组 candidates 和一个正整数 target ,找出 candidates 中所有可以使数字和为目标数 target 的唯一组合。
candidates 中的数字可以无限制重复被选取。如果至少一个所选数字数量不同,则两种组合是唯一的。
对于给定的输入,保证和为 target 的唯一组合数少于 150 个。
示例 1:
输入: candidates = [2,3,6,7], target = 7
输出: [[7],[2,2,3]]
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: []
示例 4:
输入: candidates = [1], target = 1
输出: [[1]]
示例 5:
输入: candidates = [1], target = 2
输出: [[1,1]]
提示:
- 1 <= candidates.length <= 30
- 1 <= candidates[i] <= 200
- candidate 中的每个元素都是独一无二的。
- 1 <= target <= 500
思路:
这道题和我们上面的有什么区别呢?
它没有数量要求,可以无限重复,但是有总和的限制。
这里有两个关键点:
- 元素可以重复使用
- 组合不可重复
我们看看如何通过回溯三要素来carry:
- 返回值&参数
参数里需要start标明起点,为什么呢?因为要求组合不重复,所以需要限制下次搜索的起点,是基于本次选择,这样就不会选到本次选择同层左边的数。
- 终止条件
这道题没有限制数的个数,所以我们要根据pathSum>target(当前组合不满足)和pathSum==target(当前组合满足)来终止递归。
- 单层逻辑
单层仍然从start开始,搜索 candidates。
代码:
class Solution {
//结果结合
List> result;
//结果路径
LinkedList path;
//结果路径值的和
int pathSum;
public List> combinationSum(int[] candidates, int target) {
result = new ArrayList<>();
path = new LinkedList<>();
pathSum = 0;
backtrack(candidates, target, 0);
return result;
}
public void backtrack(int[] candidates, int target, int start) {
//终止条件
if (pathSum > target) return;
if (pathSum == target) {
result.add(new LinkedList<>(path));
}
for (int i = start; i < candidates.length; i++) {
pathSum += candidates[i];
path.push(candidates[i]);
//注意,i不用加1,表示当前数可以重复读取
backtrack(candidates, target, i);
//回溯
pathSum -= path.pop();
}
}
}
⚡ 剪枝优化
又到了剪枝优化时间,在本层循环,如果发现下一层的pathSum(本层pathSum+candidates[i]),那么就可以结束本层循环,注意要先把candidates拍一下序。
class Solution {
//结果结合
List> result;
//结果路径
LinkedList path;
//结果路径值的和
int pathSum;
public List> combinationSum(int[] candidates, int target) {
result = new ArrayList<>();
path = new LinkedList<>();
pathSum = 0;
//剪枝优化,先排序
Arrays.sort(candidates);
backtrack(candidates, target, 0);
return result;
}
public void backtrack(int[] candidates, int target, int start) {
//终止条件
if (pathSum > target) return;
if (pathSum == target) {
result.add(new LinkedList<>(path));
}
//剪枝优化,判断循环之后的pathSum是否会超过target
for (int i = start; i < candidates.length && pathSum + candidates[i] <= target; i++) {
pathSum += candidates[i];
path.push(candidates[i]);
//注意,i不用加1,表示当前数可以重复读取
backtrack(candidates, target, i);
//回溯
pathSum -= path.pop();
}
}
}
LeetCode40. 组合总和 II
☕ 题目:40. 组合总和 II
❓ 难度:中等
描述:
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
注意:解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]
提示:
- 1 <= candidates.length <= 100
- 1 <= candidates[i] <= 50
- 1 <= target <= 30
思路:
这道题和上一道题有啥区别呢?
candidates里每个数字在每个组合里只能使用一次candidates里的元素是有重复的
所以这道题的关键在于:集合(数组candidates)有重复元素,但还不能有重复的组合。
关于这个去重,有什么思路呢?
- 利用
HashSet的特性去重,但是容易超时 - 还有一种办法,先把数组排序[1,3,1] --> [1,1,3],我们比较一下相邻的元素,重复的就跳过
我们把模拟树画一下:
三要素走起:
- 返回值&参数
和上一道基本一致。
- 终止条件
- pathSum>target和pathSum==target。
- 我们这次直接剪枝,提前判断下次pathSum是否大于target,所以pathSum>target可以省略
代码:
class Solution {
//结果集合
List> result;
//结果路径
LinkedList path;
//结果路径值总和
int pathSum;
public List> combinationSum2(int[] candidates, int target) {
//排序condidates,去重前提
Arrays.sort(candidates);
//初始化相关变量
result = new ArrayList<>();
path = new LinkedList<>();
pathSum = 0;
backtrack(candidates, target, 0);
return result;
}
public void backtrack(int[] candidates, int target, int start) {
//终止条件
if (pathSum == target) {
result.add(new LinkedList<>(path));
return;
}
//剪枝操作
for (int i = start; i < candidates.length && candidates[i] + pathSum <= target; i++) {
//同一层使用过的元素跳过
if (i > start && candidates[i] == candidates[i - 1]) {
continue;
}
pathSum += candidates[i];
path.push(candidates[i]);
//每个数字在每个组合中只能用一次,所以i++
backtrack(candidates, target, i + 1);
//回溯
pathSum -= path.pop();
}
}
}
LeetCode17. 电话号码的字母组合
☕ 题目:17. 电话号码的字母组合
❓ 难度:中等
描述:
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
示例 1:
输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2:
输入:digits = ""
输出:[]
示例 3:
输入:digits = "2"
输出:["a","b","c"]
提示:
- 0 <= digits.length <= 4
- digits[i] 是范围 ['2', '9'] 的一个数字。
思路:
其实扒开表皮,这道题和77.组合本质上是一样。只不过序列和组合个数没有明确给出。
- 序列是什么:digits 映射成的字母序列
- 组合个数:digits的大小
先画抽象树:
代码:
class Solution {
//结果集合
List result;
//结果
StringBuilder path;
//每个路径个数
int pathNum;
//映射数组,0,1空出来,方便直接映射
String[] numsMap = {" ", " ", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
public List letterCombinations(String digits) {
result = new ArrayList<>();
if (digits == null || digits.length() == 0) {
return result;
}
path = new StringBuilder();
pathNum = 0;
backtrack(digits, pathNum);
return result;
}
public void backtrack(String digits, int pathNum) {
if (pathNum == digits.length()) {
result.add(path.toString());
return;
}
//获取映射字母
String letters = numsMap[digits.charAt(pathNum) - '0'];
for (int i = 0; i < letters.length(); i++) {
path.append(letters.charAt(i));
//注意,pathNum+1,要处理下一层
backtrack(digits, pathNum + 1);
//回溯
path.deleteCharAt(path.length() - 1);
}
}
}
分割问题
LeetCode131. 分割回文串
☕ 题目:131. 分割回文串
❓ 难度:中等
描述:
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
示例 1:
输入:s = "aab"
输出:[["a","a","b"],["aa","b"]]
示例 2:
输入:s = "a"
输出:[["a"]]
提示:
- 1 <= s.length <= 16
- s 仅由小写英文字母组成
思路:
我们写了一些组合问题,现在又是一类新的问题——分割。
但其实,分割问题,也类似组合。
例如对于字符串abcdef:[1]
- 组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中在选组第三个.....。
- 切割问题:切割一个a之后,在bcdef中再去切割第二段,切割b之后在cdef中在切割第三段…….
先画一下抽象树:
回溯三要素:
- 参数
我们需要一个start来标记下一轮递归遍历的起始位置。
- 终止条件
如果start已经超过字符串的长度,那么说明我们path中的组合是回文串。
- 单层逻辑
单层逻辑和之前的逻辑大体类似,不过需要判断一下字符串是否是回文串,这个比较简单。
代码:
class Solution {
List> result;
LinkedList path;
public List> partition(String s) {
result = new ArrayList<>();
path = new LinkedList<>();
backtrack(s, 0);
return result;
}
public void backtrack(String s, int start) {
//结束条件
if (start >= s.length()) {
result.add(new ArrayList<>(path));
return;
}
for (int i = start; i < s.length(); i++) {
//如果是回文串
if (isPalidrome(s, start, i)) {
String r = s.substring(start, i+1);
path.addLast(r);
} else {
continue;
}
//起始位置后移
backtrack(s, i + 1);
//回溯
path.removeLast();
}
}
//判断是否回文串
boolean isPalidrome(String s, int start, int end) {
for (int i = start, j = end; i < j; i++, j--) {
if (s.charAt(i) != s.charAt(j)) {
return false;
}
}
return true;
}
}
LeetCode93. 复原 IP 地址
☕ 题目:93. 复原 IP 地址
❓ 难度:中等
描述:
给定一个只包含数字的字符串,用以表示一个 IP 地址,返回所有可能从 s 获得的 有效 IP 地址 。你可以按任何顺序返回答案。
有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
例如:"0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址,但是 "0.011.255.245"、"192.168.1.312" 和 "[email protected]" 是 无效 IP 地址。
示例 1:
输入:s = "25525511135"
输出:["255.255.11.135","255.255.111.35"]
示例 2:
输入:s = "0000"
输出:["0.0.0.0"]
示例 3:
输入:s = "1111"
输出:["1.1.1.1"]
示例 4:
输入:s = "010010"
输出:["0.10.0.10","0.100.1.0"]
示例 5:
输入:s = "101023"
输出:["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]
提示:
- 0 <= s.length <= 3000
- s 仅由数字组成
思路:
这道题是不是和上一道题类似啊。
我们先把抽象树画一下:
分支比较多,偷懒省去了一些分支。
直接上回溯三要素:
- 参数
因为ip为四段构成,所以我们需要一个参数来记录段数,这里用的是剩余的段数residue;
分割问题,需要标记start。
- 终止条件
终止条件是切割到了终点;
但是这道题又有段数的要求,所以还要加入段数的判断。
- 单层
单层里面,除了回溯之类,我们还要判断当前段是否满足构成ip的要求。
代码:
class Solution {
List res = new ArrayList<>();
Deque path = new ArrayDeque<>(4);
int len;
public List restoreIpAddresses(String s) {
len = s.length();
if (len > 12 || len < 4) return res;
backtrack(s, 0, 4);
return res;
}
/**
*
* @param s 字符串
* @param start 起始位置
* @param residue 剩余段数
*/
private void backtrack(String s, int start, int residue) {
//符合要求
//字符已经用完,而且为四段
if (start == len && residue == 0) {
res.add(String.join(".", path));
return;
}
for (int i = start; i < start + 3; i++) {
if (i >= len) break;
//减枝
if (residue * 3 < len - i) continue;
//只有符合要求的才加入
if (isIpSegment(s, start, i)) {
String currentIpSegment = s.substring(start, i + 1);
path.addLast(currentIpSegment);
backtrack(s, i + 1, residue - 1);
//回溯
path.removeLast();
}
}
}
//判断字串是否符合ip要求
private boolean isIpSegment(String s, int left, int right) {
//首位0情况
if (right - left + 1 > 1 && s.charAt(left) == '0') return false;
//判断对应数字是否满足范围
int num = 0;
for (int i = left; i <= right; i++) {
num = num * 10 + s.charAt(i) - '0';
}
return num >= 0 && num <= 255;
}
}
子集问题
LeetCode78. 子集
☕ 题目:78. 子集
❓ 难度:中等
描述:
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
提示:
- 1 <= nums.length <= 10
- -10 <= nums[i] <= 10
- nums 中的所有元素 互不相同
思路:
这和我们前面做的 77.组合也是类似得。
先画抽象树结构:
还是回溯三要素:
- 参数
组合不重复,所以start标记起点
- 终止条件
把数组所有元素用完,就终止递归,也就是start走到了最后一个位置。
- 单层逻辑
就一点需要注意,需要收集所有得组合。
代码:
class Solution {
List> result = new ArrayList<>();
LinkedList path = new LinkedList<>();
public List> subsets(int[] nums) {
if (nums == null || nums.length == 0) {
return result;
}
backstrck(nums, 0);
return result;
}
public void backstrck(int[] nums, int start) {
//放在最上面,否则漏掉本次
result.add(new ArrayList<>(path));
//终止条件
if (start >=nums.length) {
return;
}
for (int i = start; i LeetCode90. 子集 II
☕ 题目:90. 子集 II
❓ 难度:中等
描述:
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
示例 1:
输入:nums = [1,2,2]
输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
提示:
- 1 <= nums.length <= 10
- -10 <= nums[i] <= 10
思路:
和上一道题有一点不一样,nums里面有重复的元素,而要保持组合的惟一,我们得想一个去重的办法。
前面的40. 组合总和 II 还记得吗?那道题里序列里同样有重复的元素。
我们是怎么去重的呢?先排序数组,相邻元素重复就跳过。
代码:
class Solution {
List> result = new ArrayList<>();
LinkedList path = new LinkedList<>();
public List> subsetsWithDup(int[] nums) {
if (nums == null || nums.length == 0) {
result.add(new ArrayList<>());
return result;
}
//先排序数组
Arrays.sort(nums);
backtrack(nums, 0);
return result;
}
public void backtrack(int[] nums, int start) {
result.add(new ArrayList<>(path));
//终止条件
if (start >= nums.length) {
return;
}
for (int i = start; i < nums.length; i++) {
//先判断是否重复
if (i > start && nums[i] == nums[i - 1]) {
continue;
}
path.addLast(nums[i]);
backtrack(nums, i + 1);
//回溯
path.removeLast();
}
}
}
LeetCode491. 递增子序列
☕ 题目:491. 递增子序列
❓ 难度:中等
描述:
给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。
数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一种特殊情况。
示例 1:
输入:nums = [4,6,7,7]
输出:[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]
示例 2:
输入:nums = [4,4,3,2,1]
输出:[[4,4]]
提示:
- 1 <= nums.length <= 15
- -100 <= nums[i] <= 100
思路:
这道题乍一看,递增?直接套90.子集II,当然,肯定是不行的。
注意啊,我们这个整数数组是不能改变次序的,
所以上面我们用排序的方式去重在这里用不上。
那怎么办呢?
我们需要用一个结构来保存每一层用过的元素,来给它去重。
我们可以选择用map来存储用过的元素,来给每一层的循环去重。
回溯三要素:
- 参数
组合不重复,需要start。
- 终止条件
遍历完nums。
- 单层逻辑
- 去重
用map存储一层里用过的元素,选择元素之前,判断元素是否用过。
- 递增
每个元素和队尾元素比一下,判断是否满足递增的要求。
代码:
class Solution {
List> result = new ArrayList<>();
LinkedList path = new LinkedList();
public List> findSubsequences(int[] nums) {
if (nums == null || nums.length == 0) {
result.add(new ArrayList<>());
return result;
}
backtrack(nums, 0);
return result;
}
public void backtrack(int[] nums, int start) {
//使用map辅助去重
Map map = new HashMap<>();
if (path.size() > 1) {
result.add(new ArrayList<>(path));
}
if (start >= nums.length) {
return;
}
for (int i = start; i < nums.length; i++) {
//判断当前元素序列是否递增
if (!path.isEmpty() && path.getLast() > nums[i]) {
continue;
}
//本层循环元素已经用过,去重
if (map.containsKey(nums[i])) {
continue;
}
path.addLast(nums[i]);
map.put(nums[i], i);
backtrack(nums, i + 1);
path.removeLast();
}
}
}
排列问题
LeetCode46. 全排列
☕ 题目:46. 全排列
❓ 难度:中等
描述:
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1]
输出:[[1]]
提示:
- 1 <= nums.length <= 6
- -10 <= nums[i] <= 10
- nums 中的所有整数 互不相同
思路:
这里注意,我们在每一层去重。
我们之前用过两种方法去重:排序去重、map去重。
这用一个新的办法,用一个boolean数组used标记元素是否被用过。
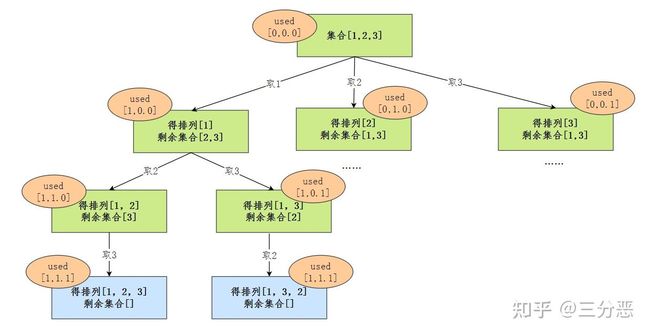
先画抽象树:
回溯三部曲:
- 结束条件
path中取到了等于集合得数量.
- 参数
注意啊,因为这里要从头开始搜索,所以就不用start了;
我们去重用的used数组直接定义全局变量;
- 单层逻辑
需要根据used数组判断当前元素是否用过。
代码:
class Solution {
List> result = new ArrayList<>();
LinkedList path = new LinkedList<>();
boolean[] used;
public List> permute(int[] nums) {
if (nums == null || nums.length == 0) {
result.add(path);
return result;
}
used = new boolean[nums.length];
backtrack(nums);
return result;
}
public void backtrack(int[] nums) {
if (path.size() == nums.length) {
result.add(new ArrayList<>(path));
return;
}
for (int i = 0; i < nums.length; i++) {
//去重判断
if (used[i]) {
continue;
}
//标记用过
used[i] = true;
path.addLast(nums[i]);
backtrack(nums);
//回溯
used[i] = false;
path.removeLast();
}
}
}
LeetCode47. 全排列 II
☕ 题目:47. 全排列 II (https://leetcode-cn.com/problems/permutations-ii/)
❓ 难度:中等
描述:
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
提示:
- 1 <= nums.length <= 8
- -10 <= nums[i] <= 10
思路:
这道题在上一道题的基础上:给定一个可包含重复数字的序列 nums。
又到了我们喜闻乐见的去重时间,这个去重是单层的去重。
这次我们可以使用排序,相邻元素比较的方式去重。
先画抽象树:
代码:
class Solution {
List> result = new ArrayList<>();
LinkedList path = new LinkedList<>();
boolean[] used;
public List> permuteUnique(int[] nums) {
if (nums == null || nums.length == 0) {
result.add(path);
return result;
}
//排序无序集合
Arrays.sort(nums);
used = new boolean[nums.length];
backtrack(nums);
return result;
}
public void backtrack(int[] nums) {
if (path.size() == nums.length) {
result.add(new ArrayList<>(path));
return;
}
for (int i = 0; i < nums.length; i++) {
//判断元素本层是否用过
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
continue;
}
//判断元素本枝干是否用过
if (used[i]) {
continue;
}
//开始处理
//标记同一个枝干用过
used[i] = true;
path.addLast(nums[i]);
backtrack(nums);
//回溯
path.removeLast();
used[i] = false;
}
}
}
棋盘问题
LeetCode51. N 皇后
☕ 题目:51. N 皇后
❓ 难度:困难
描述:
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
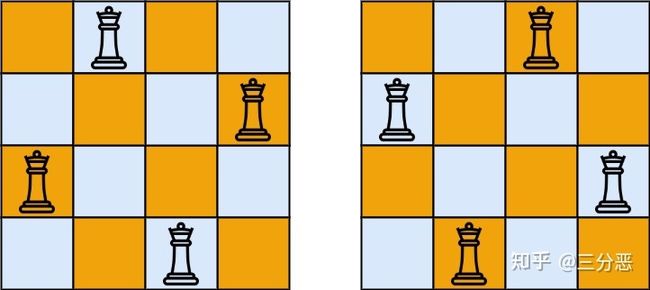
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:[["Q"]]
提示:
1 <= n <= 9- 皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
思路:
首先看一下,每个组合又什么限制呢?
- 不能同行
- 不能同列
- 不能在同一条斜线
搜索皇后的位置,同样可以抽象成一棵树。
矩阵的高就是树的高度,矩阵的宽就是每一个节点的宽度。
我们拿皇后的约束条件来剪枝,只要能搜索到树的叶子节点,那么就说明找到和合适的位置。
回溯三要素上吧!
- 参数
需要一个二维数组表示棋盘;
参数n记录棋盘大小;
用row记录遍历到棋盘的第几层;
- 终止条件
到了最底的一层,说明找到合适的皇后的位置;
- 单层逻辑
需要判断当前选择是否符合N皇后约束条件;
三个条件,行不用管,因为我们是一行一行往下的。
只需要判断左上角斜方向,列方向,右上角斜方向。
代码:
class Solution {
List> result = new ArrayList<>();
public List> solveNQueens(int n) {
//棋盘
char[][] board = new char[n][n];
//初始化棋盘
for (char[] c : board) {
Arrays.fill(c, '.');
}
backtrack(board, n, 0);
return result;
}
public void backtrack(char[][] board, int n, int row) {
//终止条件,到底了
if (row == n) {
result.add(arrayToList(board));
return;
}
for (int col = 0; col < n; col++) {
//判断是否符合N皇后要求
if (!isValid(board, n, row, col)) continue;
//开始操作
board[row][col] = 'Q';
backtrack(board, n, row + 1);
//回溯
board[row][col] = '.';
}
}
//判断当前位置是否满足N皇后要求
public boolean isValid(char[][] board, int n, int row, int col) {
//行不用判断,每层只有一个
//col列判断
for (int k = 0; k < n; k++) {
if (board[k][col] == 'Q') {
return false;
}
}
//检查主对角线(45度)
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (board[i][j] == 'Q') {
return false;
}
}
//检查副对角线(135度)
for (int i = row - 1, j = col + 1; i >= 0 && j <= n - 1; i--, j++) {
if (board[i][j] == 'Q') {
return false;
}
}
return true;
}
//将棋盘数组转换为字符串列表
public List arrayToList(char[][] board) {
List path = new ArrayList<>();
for (char[] c : board) {
path.add(String.valueOf(c));
}
return path;
}
}
LeetCode 37. 解数独
☕ 题目:37. 解数独
❓ 难度:困难
描述:
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
- 数字 1-9 在每一行只能出现一次。
- 数字 1-9 在每一列只能出现一次。
- 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 '.' 表示。
输入:board = [["5","3",".",".","7",".",".",".","."], ["6",".",".","1","9","5",".",".","."], [".","9","8",".",".",".",".","6","."], ["8",".",".",".","6",".",".",".","3"], ["4",".",".","8",".","3",".",".","1"], ["7",".",".",".","2",".",".",".","6"], [".","6",".",".",".",".","2","8","."], [".",".",".","4","1","9",".",".","5"], [".",".",".",".","8",".",".","7","9"]]
输出:[["5","3","4","6","7","8","9","1","2"], ["6","7","2","1","9","5","3","4","8"], ["1","9","8","3","4","2","5","6","7"], ["8","5","9","7","6","1","4","2","3"], ["4","2","6","8","5","3","7","9","1"], ["7","1","3","9","2","4","8","5","6"], ["9","6","1","5","3","7","2","8","4"], ["2","8","7","4","1","9","6","3","5"], ["3","4","5","2","8","6","1","7","9"]]
解释:输入的数独如上图所示,唯一有效的解决方案如下所示:
提示:
- board.length == 9
- board[i].length == 9
- board[i][j] 是一位数字或者 '.'
- 题目数据 保证 输入数独仅有一个解
思路:
这道题可以说是N皇后问题的plu版本了。
这道题矩阵的长度和宽度都比N皇后更长更宽。
而且判断重复也更难:
- 同行是否重复
- 同列是否重复
- 9宫格里是否重复
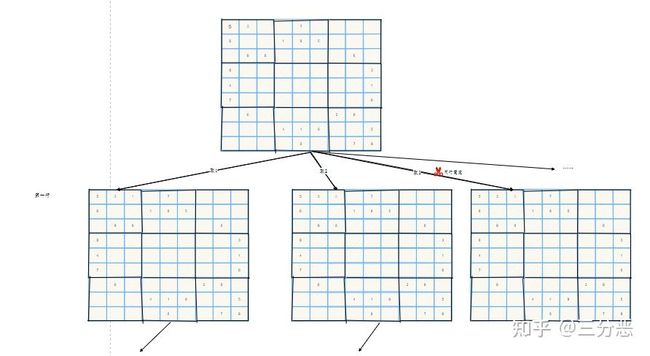
我们先大概画一棵抽象树:
这个图画起来太麻烦了,差不多就那个意思,接下来我们三部曲走起[1]。
- 返回值与参数
因为解数独找到一个符合的条件就返回,所以返回值用boolean类型。
- 终止条件
可以不用终止条件,因为
- 单层逻辑
需要一个两个循环套着的递归,一个循环棋盘的行,一个循环棋盘的列,递归遍历这个位置放9个数字的可能。
代码:
class Solution {
public void solveSudoku(char[][] board) {
backtrack(board);
}
boolean backtrack(char[][] board) {
//遍历行
for (int row = 0; row < board.length; row++) {
//遍历列
for (int col = 0; col < board[0].length; col++) {
if (board[row][col] != '.') continue;
//尝试1-9
for (char k = '1'; k <= '9'; k++) {
//不满足,跳过
if (!isValid(board, row, col, k)) continue;
//满足要求操作
board[row][col] = k;
//找到一组,立即返回
if (backtrack(board)) {
return true;
}
//回溯,撤销填入
board[row][col] = '.';
}
//9个数试完了,不行,返回false
return false;
}
}
return true;
}
//判断是否符合数独要求
boolean isValid(char[][] board, int row, int col, char val) {
//判断行是否重复
for (int i = 0; i < 9; i++) {
if (board[row][i] == val) {
return false;
}
}
//判断列是否重复
for (int j = 0; j < 9; j++) {
if (board[j][col] == val) {
return false;
}
}
//判断小9宫格是否重复
int startRow = (row / 3) * 3;
int startCol = (col / 3) * 3;
for (int i = startRow; i < startRow + 3; i++) {
for (int j = startCol; j < startCol + 3; j++) {
if (board[i][j] == val) {
return false;
}
}
}
return true;
}
}
总结
接着顺口溜总结: