吴恩达机器学习exercise笔记
参考这里入下门,主要包括代码逻辑、numpy、pandas、scipy等的使用。
ML-Exercise1
X = np.matrix(X.values)
DataFrame.values(旧), DataFrame.to_numpy()用于将pandas中的dataframe转为numpy中的数组。
更新:exercise5中将数据框转化数组使用了已经淘汰的DataFrame.as_matrix(),实际应该使用DataFrame.values。推测转化为pandas数组推荐该属性,而转为numpy中数组推荐上面的方法。
X = data.iloc[:,0:cols-1]#X是所有行,去掉最后一列
y = data.iloc[:,cols-1:cols]#X是所有行,最后一列
pandas.DataFrame.iloc选定不部分行和列,注意y可以写成data.iloc[:,[cols-1]],效果相同;但如果写成data.iloc[:,cols-1],则y不再是dataframe,而是series。
ML-Exercise2
positive = data[data['Admitted'].isin([1])]
pandas.DataFrame.isin Return DataFrame of booleans showing whether each element in the DataFrame is contained in values.
相当于对data的行根据’Admitted’列是否为1进行筛选。
对数几率回归代价函数:
J ( θ ) = 1 m ∑ i = 1 m [ − y ( i ) log ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{[-{{y}^{(i)}}\log \left( {{h}_{\theta }}\left( {{x}^{(i)}} \right) \right)-\left( 1-{{y}^{(i)}} \right)\log \left( 1-{{h}_{\theta }}\left( {{x}^{(i)}} \right) \right)]} J(θ)=m1i=1∑m[−y(i)log(hθ(x(i)))−(1−y(i))log(1−hθ(x(i)))]
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def cost(theta, X, y):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
return np.sum(first - second) / (len(X))
np.exp(), np.log()等函数对矩阵操作即对每个元素进行操作;
1 - y:矩阵等与常数加减即对每个元素加减;
X行为不同数据,列为属性;直接将X与一列theta的转置相乘,得到一列预测的y。这一列与真实的y或者(1-y)相乘,使用np.multiply(),使得两个一列的矩阵对应位置相乘;得到的一列的矩阵再使用np.sum(),将该矩阵所有元素相加,实现了 ∑ i = 1 m \sum\limits_{i=1}^{m} i=1∑m。
用SciPy’s truncated newton(TNC)实现寻找最优参数:
import scipy.optimize as opt
result = opt.fmin_tnc(func=cost, x0=theta, fprime=gradient, args=(X, y))
其中gradient函数返回值为一个对应theta的array,代表每个theta的梯度: ∂ J ( θ ) ∂ θ j = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial J\left( \theta \right)}{\partial {{\theta }_{j}}}=\frac{1}{m}\sum\limits_{i=1}^{m}{({{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}})x_{_{j}}^{(i)}} ∂θj∂J(θ)=m1i=1∑m(hθ(x(i))−y(i))xj(i)。
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)]
计算分类预测的精确度,zip函数用于将可迭代的对象作为参数,将对象中对应的元素打包成一个个元组,然后返回由这些元组组成的列表。
ML-Exercise3
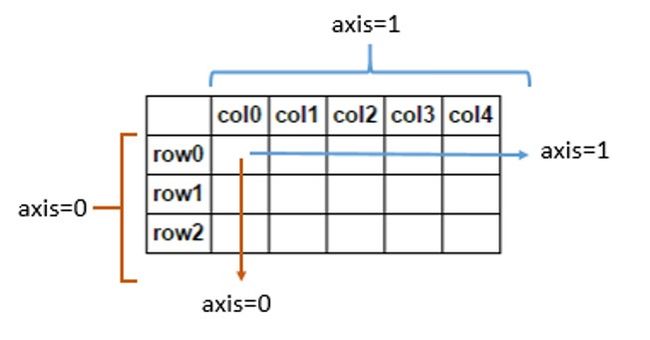
axis取0代表最外层(行),1,2,3···依次为内层结构;
在二维矩阵中,axis=0代表跨行(down),而axis=1代表跨列(across),如:
X = np.insert(X, 0, values=np.ones(rows), axis=1)
在矩阵X的每一行的第0个元素前插入一元素1,相当于插入一列;
h_argmax = np.argmax(h, axis=1)
返回矩阵中每一行最大值的列索引。
同样地,求均值、综合等操作,都可以看作dataframe在axis轴上的降维操作。
ML-Exercise4

ML-Exercise5
numpy中“@”作为矩阵相乘符号;
def load_data:
d=sio.loadmat('ex5data.mat')
return map(np.ravel, [d['X'], d['y'], d['Xval'], d['yval'], d['Xtest'], d['ytest']])
X, y, Xval, yval, Xtest, ytest = load_data()
map() 会根据提供的函数对指定序列做映射。
第一个参数 function 以参数序列中的每一个元素调用 function 函数,返回包含每次 function 函数返回值的新列表。
本例中,对d[‘X’]等均进行ravel操作转为一维数组,之后分别返回。
def prepare_poly_data(*args, power):
def prepare(x):
df = poly_features(x, power=power)
ndarr = normalize_feature(df).as_matrix()
return np.insert(ndarr, 0, np.ones(ndarr.shape[0]), axis=1)
return [prepare(x) for x in args]
*args 表示任何多个无名参数,它是一个tuple;**kwargs 表示关键字参数,它是一个dict。本例中对多个集合进行该操作只需要一行:
X_poly, Xval_poly, Xtest_poly= prepare_poly_data(X, Xval, Xtest, power=8)
data = {'f{}'.format(i): np.power(x, i) for i in range(1, power + 1)}
data为一字典,元素由for…in…迭代生成,元素的key为’f1’、‘f2’…
def linear_regression_np(X, y, l=1):
···
res = opt.minimize(fun=regularized_cost,
x0=theta,
args=(X, y, l),
method='TNC',
jac=regularized_gradient,
options={'disp': True})
···
函数形参中的l=1为默认值,不指定该参数则使用默认值属性;scipy.optimize函数中arg属性元组参数为fun和jac属性的函数的对应参数。