前缀和（C/C++）

目录

1. 前缀和的定义

2. 一维前缀和

2.1 计算公式

2.2 用途

         2.3 小试牛刀 

3. 二维前缀和

3.1 用途

---

 

1. 前缀和的定义

对于一个给定的数列A，他的前缀和数中 S 中 S[ i ] 表示从第一个元素到第 i 个元素的总和。

如下图：绿色区域的和就是前缀和数组中的 S [ 6 ]。

 这里你可能就会有一个疑问？为什么是 S[ 6 ] 的位置，而不是 S[ 5 ] 的位置呢？？即前缀和组中 S[ 0 ] 并没有参与求和的运算。这里先卖个关子等会在做解释。

2. 一维前缀和

2.1 计算公式

前缀和数组的每一项是可以通过原序列以递推的方式推出来的，递推公式就是：S[ i ] = S[  i - 1 ] + A[ i ]。S[  i - 1 ] 表示前 i - 1 个元素的和，在这基础上加上 A[ i ]，就得到了前 i 个元素的和 S [ i ]。

2.2 用途

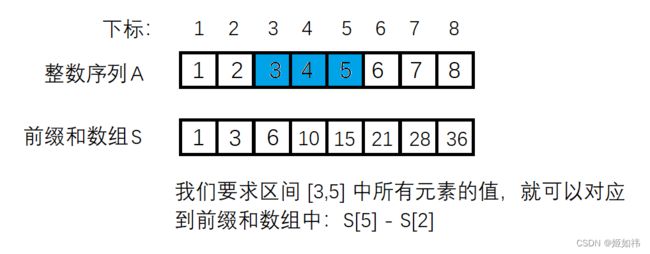
一维前缀和的主要用途：求一个序列中某一段区间中所有元素的和。有如下例子：

有一个长度为 n 的整数序列。

接下来输入 m 个询问，每个询问输入一对 l，r。

对于每个询问，输出原序列中第 l 个数到第 r 个数的和。

这边是对前缀和的应用，如果用常规的方法：从 l 到 r 遍历一遍，则需要O(N)的时间复杂度。但是有前缀和数组的话，我们可以直接利用公式：sum = S[ r ] - S[ l - 1 ]，其中sum是区间中元素的总和，l 和 r 就是区间的边界。下图可帮助理解这个公式。

 当我们要求的是序列 A 的前 n 个数之和时，如果我们是从下标为 0 的位置开始存储前缀和数组，此公式：sum = S[ r ] - S[ l - 1 ] 显然就无法使用了，为了是这个公式适用于所有情况，我们将从下标为 1 的位置开始存储前缀和，并且将下标为 0 的位置初始化为 0。

 

 这便是为什么 S[ 0 ] 并未参与求和的运算。

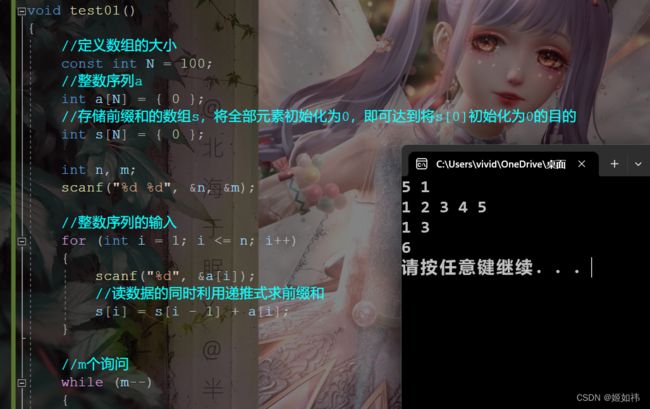
有了上面的分析我们就能轻松解决这道题啦！

有一个长度为 n 的整数序列。

接下来输入 m 个询问，每个询问输入一对 l，r。

对于每个询问，输出原序列中第 l 个数到第 r 个数的和。

 

输入格式

第一行包含两个整数n和m。

第二行包含n个整数，表示整数数列。

接下来m行，每行包含两个整数l和r，表示一个询问区间的范围。

void test01()
{
	//定义数组的大小
	const int N = 100;
	//整数序列a
	int a[N] = { 0 };
	//存储前缀和的数组s，将全部元素初始化为0，即可达到将s[0]初始化为0的目的
	int s[N] = { 0 };
	
	int n, m;
	scanf("%d %d", &n, &m);

	//整数序列的输入
	for (int i = 1; i <= n; i++)
	{
		scanf("%d", &a[i]);
		//读数据的同时利用递推式求前缀和
		s[i] = s[i - 1] + a[i];
	}

	//m个询问
	while (m--)
	{
		int l, r;
		scanf("%d %d", &l, &r);
		//利用求区间元素个数的通式计算结果
		printf("%d\n", s[r] - s[l - 1]);
	}

}

int main()
{
	//一维前缀和
	test01();

	system("pause");
	return 0;
}

 2.3 小试牛刀 

原题链接：

209. 长度最小的子数组 - 力扣（LeetCode）https://leetcode.cn/problems/minimum-size-subarray-sum/

题目描述：

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组，并返回其长度。如果不存在符合条件的子数组，返回 0 。

3. 二维前缀和

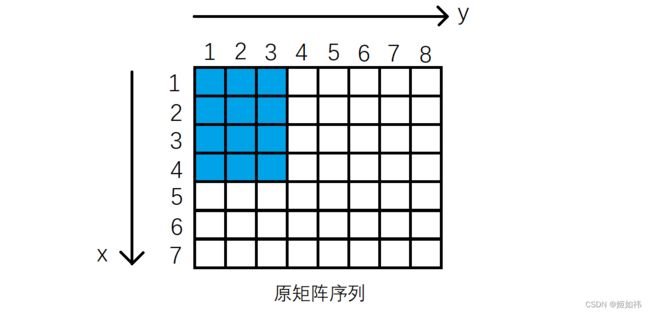
和一维前缀和的原理类似，只不过二维前缀和求的是一个矩阵中所有元素的和。

 例如：对与 x = 4，y = 3 这么一组输入，就是将原矩阵序列中蓝色区域的元素相加，得到的结果便是前缀和矩阵S中 S[ 4 ][ 3 ] 的值。

3.1 用途

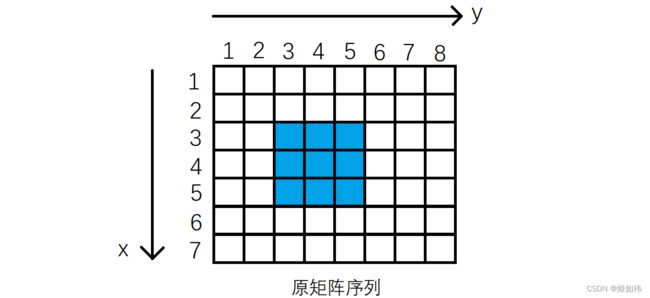
一维前缀和求的是某一个区间中所有元素的和，那么二维前缀和就是求一个大矩阵中某个小的矩阵中所有元素的和。

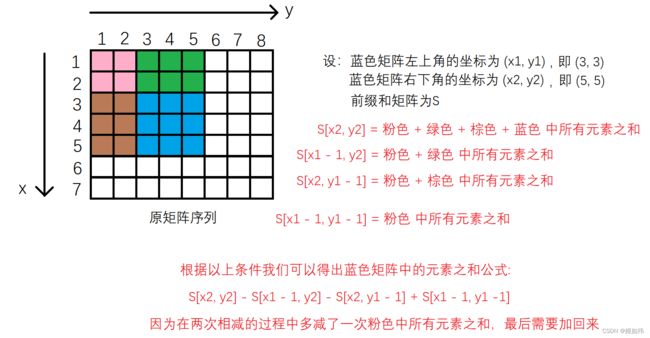
 例如上图：我们要求蓝色矩阵中所有元素的和。

 现在就差最后一步了，怎么求出前缀和矩阵中的每一个值嘞？？同理利用递推关系求就阔以啦。

                            S[ i ][ j ] = S[ i - 1 ][ j ] + S[ i ][ j - 1 ] - S[ i - 1][ j - 1 ] + a[ i ][ j ]

其中a为原矩阵序列。可以尝试举一个具体的例子来理解。

有了以上知识，我们可以尝试写代码求一下。

输入一个n行m列的矩阵，在输入q个询问，每个询问包含四个整数x1，y1，x2，y2，表示一个子矩阵左上角的坐标和右下角的坐标。

对于每个询问输出子矩阵中所有数的和。

 

输入格式

第一行包含三个整数n，m，q

接下来n行，每行包含m个整数，表示整数矩阵。

接下来q行，每行包含四个整数x1，y1，x2，y2，表示一组询问。

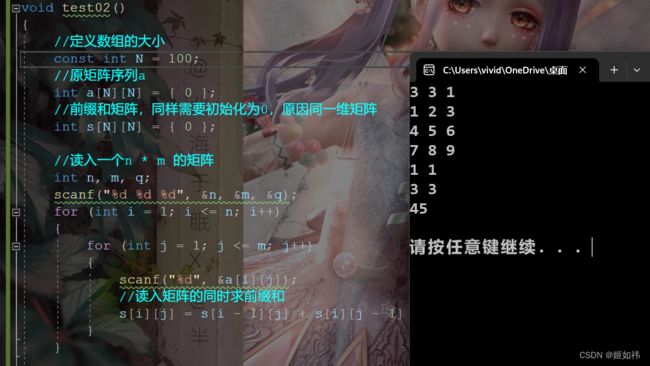
void test02()
{
	//定义数组的大小
	const int N = 100;
	//原矩阵序列a
	int a[N][N] = { 0 };
	//前缀和矩阵，同样需要初始化为0，原因同一维矩阵
	int s[N][N] = { 0 };

	//读入一个n * m 的矩阵
	int n, m, q;
	scanf("%d %d %d", &n, &m, &q);
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			scanf("%d", &a[i][j]);
			//读入矩阵的同时求前缀和
			s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
		}
	}

	//q个询问
	while (q--)
	{
		int x1, y1, x2, y2;
		scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
		//利用前面推导过的公式直接打印数据即可
		printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
	}
	printf("\n");
}


int main()
{

	//二维前缀和
	test02();

	system("pause");
	return 0;
}