LeetCode --- 动态规划（一）

LeetCode前200道题中的动态规划 

目录

LeetCode前200道题中的动态规划 

10. 正则表达式匹配

44. 通配符匹配

62. 不同路径

64. 最小路径和

72. 编辑距离

91. 解码方法

96. 不同的二叉搜索树

95. 不同的二叉搜索树 II

97. 交错字符串

115. 不同的子序列

174. 地下城游戏

---

10. 正则表达式匹配

 

比较难的一道动态规划，给出两种方法。

当前位置不是*比较容易，是*的时候要考虑可以不用前面的符号和用多次的问题。

class Solution {
public:
    bool match(char* str, char* pattern)
    {
        int m = strlen(str),n = strlen(pattern);
 
        bool dp[m+11][n+11];
        memset(dp,0,sizeof dp);
        dp[0][0] = true;
 
        for(int i = 0;i<=m;i++)
            for(int j = 1;j<=n;j++){
                if(pattern[j-1] == '*')
                    dp[i][j] = dp[i][j-2] || (i>0 && str[i-1] == pattern[j-2] || pattern[j-2] == '.') && dp[i-1][j];//不用* 或者用* &&dp[i-1][j]是因为因为*可以匹配多个
                else dp[i][j] = i>0 && (str[i-1] == pattern[j-1] || pattern[j-1] == '.') && dp[i-1][j-1];//
 
            }
 
        return dp[m][n];
    }
};


class Solution {
public:
    bool match(char* str, char* pattern)
    {
        if(*str == 0 && *pattern == 0)return true;
        if(*str != 0 && *pattern ==0)return false;//str还有，pattern 没了
         
        if(*(pattern+1) != '*'){
            if(*str == *pattern || *str != 0 && *pattern == '.'){//匹配
                return match(str+1,pattern+1);//向前走
            }
            return false;//不匹配，返回false
        }
         
        else{
            if(*str == *pattern || *str!=0 && *pattern == '.')//当前能匹配
                return match(str,pattern+2) || match(str+1,pattern);//直接跳过下个* 或者 看带着*，str继续走（可匹配多个）
            return match(str,pattern+2);
        }
         
    }
};

 

 

44. 通配符匹配

 

class Solution {
public:
    bool isMatch(string s, string p) {
        int n = s.size(), m = p.size();
        vector< vector > dp(n+1, vector(m+1,false) );
        dp[0][0] = true;
        
        for(int i = 1;i<=m;++i) if(p[i-1] == '*')
            dp[0][i] = dp[0][i-1];
        
        for(int i = 1;i<=n;++i)
            for(int j = 1;j<=m;++j){
                if(p[j-1] == '*')
                    dp[i][j] = dp[i-1][j] || dp[i][j-1];//匹配字符串或者空串
                else 
                    dp[i][j] = (s[i-1] == p[j-1] || p[j-1] == '?') && dp[i-1][j-1];
                
            }
        return dp[n][m];
        
    }
};

62. 不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

 

class Solution {
public:
    
    int uniquePaths(int m, int n) {
        
        vector< vector > dp(n, vector(m,0) );
        
        for(int i = 0;i

 

 

64. 最小路径和

 

class Solution {
public:
    int minPathSum(vector>& grid) {
        
        int n = grid.size();
        if(!n)return 0;
        int m = grid[0].size();
        vector< vector > dp(n, vector(m,0) );
        dp[0][0] = grid[0][0];
        for(int i = 0;i

 

 

72. 编辑距离

好吧，听说这届省赛出的这道题。一道经典的动态规划：

假设序列S和T的当前长度分别为m和n, 两者的编辑距离表示为dp[m][n]. 则对序列进行操作时存在以下几种情况:

 1、当S和T的末尾字符相等时, 对末尾字符不需要进行上述定义操作中(亦即"编辑")的任何一个, 也就是不需要增加计数. 则满足条件: dp[m][n] = dp[m - 1][n - 1].
 2、 当S和T的末尾字符不相等时, 则需要对两者之一的末尾进行编辑, 相应的计数会增加1.
 3、 对S或T的末尾进行修改, 以使之与T或S相等, 则此时dp[m][n] = dp[m - 1][n - 1] + 1;
 4、 删除S末尾的元素, 使S与T相等, 则此时dp[m][n] = dp[m - 1][n] + 1;
 5、 删除T末尾的元素, 使T与S相等, 则此时dp[m][n] = dp[m][n - 1] + 1;
 6、 在S的末尾添加T的尾元素, 使S和T相等, 则此时S的长度变为m+1, 但是此时S和T的末尾元素已经相等, 只需要比较S的前m个元素与T的前n-1个元素, 所以满足dp[m][n] = dp[m][n - 1] + 1;
7、 在T的末尾添加S的尾元素, 使T和S相等, 此时的情况跟b4相同, 满足dp[m][n] = dp[m - 1][n] + 1;
8、 比较特殊的情况是, 当S为空时, dp[0][n] = n; 而当T为空时, dp[m][0] = m; 这个很好理解, 例如对于序列""和"abc", 则两者的最少操作为3, 即序列""进行3次插入操作, 或者序列"abc"进行3次删除操作.
 

class Solution {
public:
    int minDistance(string word1, string word2) {
        int n = word1.size();
        int m = word2.size();
        int dp[1111][1111];
        
        for(int i = 0;i<=n;++i)dp[i][0] = i;
        for(int i = 0;i<=m;++i)dp[0][i] = i;
        
        for(int i = 1;i<=n;++i)
            for(int j = 1;j<=m;++j){
                if(word1[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1];
                else dp[i][j] = 1+min(dp[i-1][j],min(dp[i][j-1],dp[i-1][j-1]));
            }
        return dp[n][m];    
        
        
    }
};

 

 

91. 解码方法

一条包含字母 A-Z 的消息通过以下方式进行了编码：

'A' -> 1
'B' -> 2
...
'Z' -> 26

给定一个只包含数字的非空字符串，请计算解码方法的总数。

示例 1:

输入: "12"
输出: 2
解释: 它可以解码为 "AB"（1 2）或者 "L"（12）。

class Solution {
public:
    int numDecodings(string s) {
    //dp[n] = dp[n-1] + dp[n-2](n-1 n能组成)
        int n = s.size();
        int dp[111111];
        for(int i = 0;i<=n+2;i++)dp[i] = 0;
        dp[0] = 1;dp[1] = 1;
        if(s[0] == '0')dp[1] = 0;
        for(int i = 2;i <= n;i++)
        {
            dp[i] = s[i-1] == '0'? 0:dp[i-1];//当前是0 重新开始，不是的话先等于上面的
            if(  (s[i-2] == '1') || (s[i-2] == '2' && s[i-1] <= '6'  )   )//加上两位的
                dp[i] += dp[i-2];
        }
        
        return dp[n];
    
    }
};

 

96. 不同的二叉搜索树

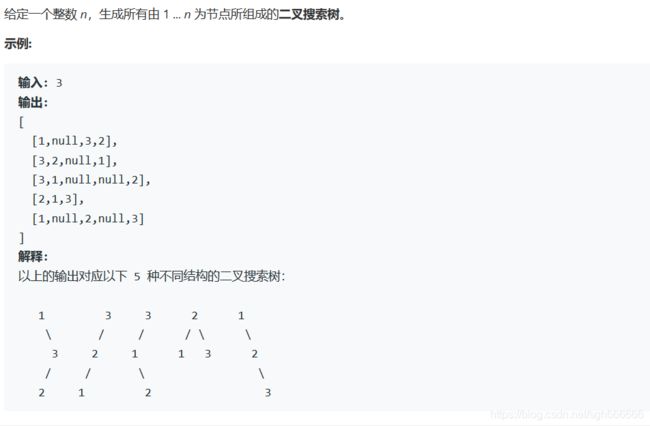
给定一个整数 n，求以 1 ... n 为节点组成的二叉搜索树有多少种？

 

dp[i] ： i个节点可以组成的二叉搜索树的个数。

可以得递推式：dp[i] = dp[0] * dp[i-1] + dp[1] * dp[i-2] * .......

初始化：dp[0] = dp[1] = 1;

class Solution {
public:
    int numTrees(int n) {
        //a[i] = a[0]*a[i-1] + a[1] * a[i-2] + ...
        
        vector dp(n+1,0);
        dp[0] = dp[1] = 1;
        
        for(int i = 2;i<=n;++i)
            for(int j = 0;j

 

 

95. 不同的二叉搜索树 II

直接搜索，不过还是要有上个题的思想的：

class Solution {
public:
    vector generateTrees(int n) {
        if(n)return solve(1,n);
        else return std::vector{};
    }


    vector solve(int left,int right){
    	std::vector v;
    	if(left > right){
    		v.push_back(nullptr);
    		return v;
    	}

    	for(int i = left;i<=right;i++){
    		std::vector left_node = solve(left,i-1);
    		std::vector right_node = solve(i+1,right);
    		for(auto x:left_node)
    			for(auto y:right_node){
    				TreeNode *t = new TreeNode(i);
    				t->left = x;
    				t->right = y;
    				v.push_back(t);
    			}
    	}

    	return v;
    }
};

 

 

 

97. 交错字符串

 

字符串上简单的动规即可：

class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {         
        int len1 = s1.size(),len2 = s2.size(),len3 = s3.size();
        
        
        if(len1+len2 != len3)return false;
        if(!len3)return true;
        
        vector< vector > dp(len1+1,vector(len2+2,0) );
        dp[0][0] = 1;
        for(int i = 1;i <= len1 && s1[i-1] == s3[i-1];++i){
            dp[i][0] = 1;
        }
        
        for(int i = 1;i <= len2 && s2[i-1] == s3[i-1];++i)
            dp[0][i]  = 1;
        
        
        for(int i = 1;i<=len1;++i)
            for(int j = 1;j<=len2;++j){
                int k = i+j-1;
                if(s1[i-1] == s3[k] && dp[i-1][j])
                    dp[i][j] = 1;
                if(s2[j-1] == s3[k] && dp[i][j-1])
                    dp[i][j] = 1;
                
            }
        
        return dp[len1][len2];
        
    }
};

 

 

 

115. 不同的子序列

 

 

字符串上简单动规：

dp[i][j] = dp[i-1][j];(不用s中当前的字符）

如果是s[i] == t[i]的话，d[i][j] += dp[i-1][j-1];

class Solution {
public:
    int numDistinct(string s, string t) {
        int n = s.size(), m = t.size();
        
        vector< vector > dp(n+2, vector(m+2,0)  );
        
        for(int i = 0;i<=n;++i)dp[i][0] = 1;
        for(int i = 1; i <= n;++i)
            for(int j = 1;j<=m;++j){
                
                if(i

 

 

 

174. 地下城游戏

一些恶魔抓住了公主（P）并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士（K）最初被安置在左上角的房间里，他必须穿过地下城并通过对抗恶魔来拯救公主。

骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下，他会立即死亡。

有些房间由恶魔守卫，因此骑士在进入这些房间时会失去健康点数（若房间里的值为负整数，则表示骑士将损失健康点数）；其他房间要么是空的（房间里的值为 0），要么包含增加骑士健康点数的魔法球（若房间里的值为正整数，则表示骑士将增加健康点数）。

为了尽快到达公主，骑士决定每次只向右或向下移动一步。

 

编写一个函数来计算确保骑士能够拯救到公主所需的最低初始健康点数。

例如，考虑到如下布局的地下城，如果骑士遵循最佳路径 右 -> 右 -> 下 -> 下，则骑士的初始健康点数至少为 7。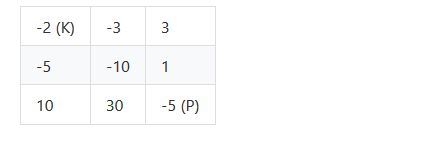

 

题解：可以采用二分（写一个判断可达函数搜索），但是本题动态规划似乎更方便：

dp[i][j] : 骑士在(i,j)的时候最少需要的健康点数。

dp[i][j] < 0代表当前位置走到终点还剩健康点数，所以可以置为0，继续往前递推。

class Solution {
public:
    int calculateMinimumHP(vector>& mp) {
        int n = mp.size(),m = mp[0].size();
        vector< vector > dp(n+1, vector(m+1,0) );
        dp[n-1][m-1] = mp[n-1][m-1] >=0 ? 0: -mp[n-1][m-1];
        for(int i = n-1;i>=0;--i)
            for(int j = m-1;j>=0;--j){
                
                int _min = 0x3f3f3f3f;
                if(i < n-1)
                    _min = min(_min,dp[i+1][j] - mp[i][j]);
                if(j < m-1)
                    _min = min(_min,dp[i][j+1] - mp[i][j]);
                
                if(i == n-1 && j == m-1);
                else dp[i][j] = max(0,_min);
            }
        
        return dp[0][0]+1;
    }
};