【LeetCode每日一题合集】2023.9.11-2023.9.17（⭐反悔贪心&拓扑排序&Floyd）

630. 课程表 III

https://leetcode.cn/problems/course-schedule-iii/description/?envType=daily-question&envId=2023-09-11

提示:
1 <= courses.length <= 10^4
1 <= durationi, lastDayi <= 10^4

解法——反悔贪心⭐⭐⭐⭐⭐

https://leetcode.cn/problems/course-schedule-iii/solutions/2436667/tan-xin-huan-neng-fan-hui-pythonjavacgoj-lcwp/?envType=daily-question&envId=2023-09-11

class Solution {
    public int scheduleCourse(int[][] courses) {
        // 按照截止时间从小到大排序
        Arrays.sort(courses, (a, b) -> a[1] - b[1]);
        // 最大堆
        PriorityQueue<Integer> pq = new PriorityQueue<>((a, b) -> b - a);
        int day = 0;        // 记录当前使用了多少天
        for (int[] c: courses) {
            int d = c[0], t = c[1];
            if (day + d <= t) {
                // 如果可以学，直接学
                day += d;
                pq.offer(d);
            } else if (!pq.isEmpty() && pq.peek() > d) {
                // 如果不可以学，检查已经选了的课程中有没有耗时更长的替换掉
                day -= pq.poll() - d;
                pq.offer(d);
            }
        }
        // 最后的答案就是队列中已选课程的数量
        return pq.size();
    }
}

更多反悔贪心可见：
【算法】反悔贪心
【力扣周赛】第 357 场周赛（⭐反悔贪心）

1462. 课程表 IV⭐

https://leetcode.cn/problems/course-schedule-iv/?envType=daily-question&envId=2023-09-12

提示：

2 <= numCourses <= 100
0 <= prerequisites.length <= (numCourses * (numCourses - 1) / 2)
prerequisites[i].length == 2
0 <= ai, bi <= n - 1
ai != bi
每一对 [ai, bi] 都 不同
先修课程图中没有环。
1 <= queries.length <= 10^4
0 <= ui, vi <= n - 1
ui != vi

解法1——拓扑排序预处理

关于拓扑排序可见：【算法基础：搜索与图论】3.3 拓扑排序
在拓扑排序过程中多加一层循环，用来处理各个节点之间是否为先决条件。 回复查询时只需要$O(1)$查询。

class Solution {
    public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {
        List<Boolean> ans = new ArrayList<>();
        List<Integer>[] g = new ArrayList[numCourses];
        int[] in = new int[numCourses];
        Arrays.setAll(g, e -> new ArrayList<Integer>());
        boolean[][] isPre = new boolean[numCourses][numCourses];
        for (int[] p: prerequisites) {
            g[p[0]].add(p[1]);
            in[p[1]]++;
            isPre[p[0]][p[1]] = true;
        }
        // 拓扑排序预处理出n^2各个节点是否是其它节点的先决条件
        Queue<Integer> q = new LinkedList<>();
        for (int i = 0; i < numCourses; ++i) {
            if (in[i] == 0) q.offer(i);
        }
        while (!q.isEmpty()) {
            int x = q.poll();
            for (int y: g[x]) {
                for (int i = 0; i < numCourses; ++i) {
                    isPre[i][y] |= isPre[i][x];
                }
                if (--in[y] == 0) q.offer(y);
            }
        }
        // O(1) 回答查询
        for (int[] query: queries) {
            ans.add(isPre[query[0]][query[1]]);
        }
        return ans;
    }
}

解法2——Floyd算法判断是否存在路径

关于Floyd算法可见：【算法基础：搜索与图论】3.4 求最短路算法（Dijkstra&bellman-ford&spfa&Floyd）

class Solution {
    public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {
        boolean[][] g = new boolean[numCourses][numCourses];
        for (int[] p: prerequisites) {
            g[p[0]][p[1]] = true;
        }
        // Floyd三重循环
        for (int k = 0; k < numCourses; ++k) {
            for (int i = 0; i < numCourses; ++i) {
                for (int j = 0; j < numCourses; ++j) {
                    g[i][j] = g[i][j] | (g[i][k] & g[k][j]);
                }
            }
        }
        // 回复查询
        List<Boolean> ans = new ArrayList<>();
        for (int[] q: queries) {
            ans.add(g[q[0]][q[1]]);
        }
        return ans;
    }
}

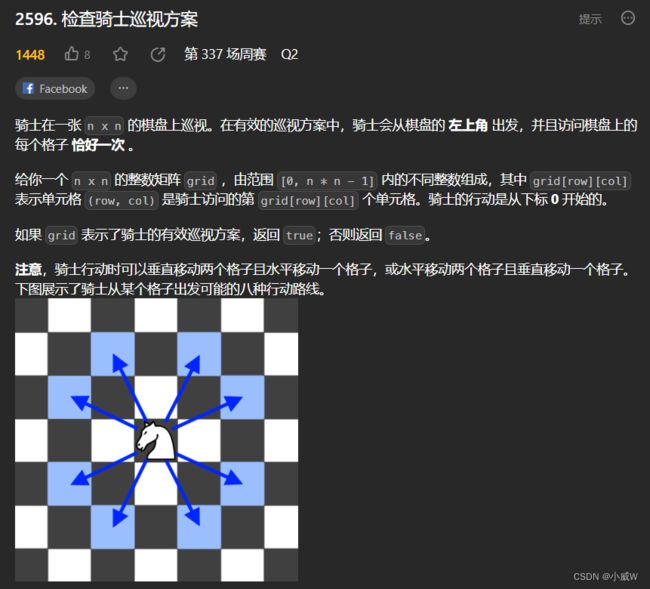
2596. 检查骑士巡视方案（方向模拟）

https://leetcode.cn/problems/check-knight-tour-configuration/?envType=daily-question&envId=2023-09-13

提示：
n == grid.length == grid[i].length
3 <= n <= 7
0 <= grid[row][col] < n * n
grid 中的所有整数 互不相同

按题意模拟八个方向即可。

class Solution {
    int[] dx = {-1, -2, -2, -1, 1, 2, 2, 1}, dy = new int[]{-2, -1, 1, 2, 2, 1, -1, -2};

    public boolean checkValidGrid(int[][] grid) {
        int n = grid.length;
        int x = 0, y = 0;
        for (int i = 0; i < n * n - 1; ++i) {   // 检查每一步
            boolean f = false;
            for (int k = 0; k < 8; ++k) {       // 尝试8个方向
                int nx = x + dx[k], ny = y + dy[k];
                if (nx >= 0 && ny >= 0 && nx < n && ny < n && grid[nx][ny] == grid[x][y] + 1) {
                    x = nx;
                    y = ny;
                    f = true;
                    break;
                }
            }
            if (!f) return false;
        }
        return true;
    }
}

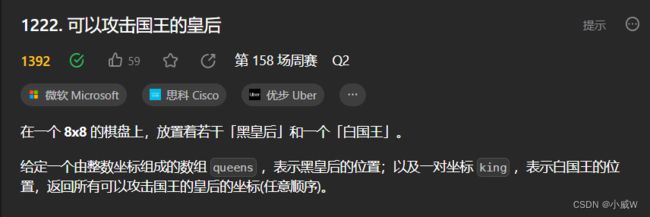
1222. 可以攻击国王的皇后（方向模拟）

https://leetcode.cn/problems/queens-that-can-attack-the-king/description/

提示：

1 <= queens.length <= 63
queens[i].length == 2
0 <= queens[i][j] < 8
king.length == 2
0 <= king[0], king[1] < 8
一个棋盘格上最多只能放置一枚棋子。

将所有皇后放入一个哈希集合中。

从国王位置开始，枚举8个方向，走8步，如果遇到的位置存在于皇后集合中，则将其加入答案。

class Solution {
    public List<List<Integer>> queensAttacktheKing(int[][] queens, int[] king) {
        List<List<Integer>> ans = new ArrayList<>();
        Set<Integer> s = new HashSet<>();
        for (int[] q: queens) s.add(q[0] * 10 + q[1]);
        int[] dx = {-1, -1, 0, 1, 1, 1, 0, -1}, dy = {0, 1, 1, 1, 0, -1, -1, -1};
        int x = king[0], y = king[1];
        for (int i = 0; i < 8; ++i) {           // 枚举8个方向
            for (int k = 1; k < 8; ++k) {       // 枚举8步
                int nx = x + dx[i] * k, ny = y + dy[i] * k;
                if (nx >= 0 && ny >= 0 && nx < 8 && ny < 8) {
                    if (s.contains(nx * 10 + ny)) {
                        ans.add(List.of(nx, ny));
                        break;
                    }
                } else break;
            }
        }
        return ans;
    }
}

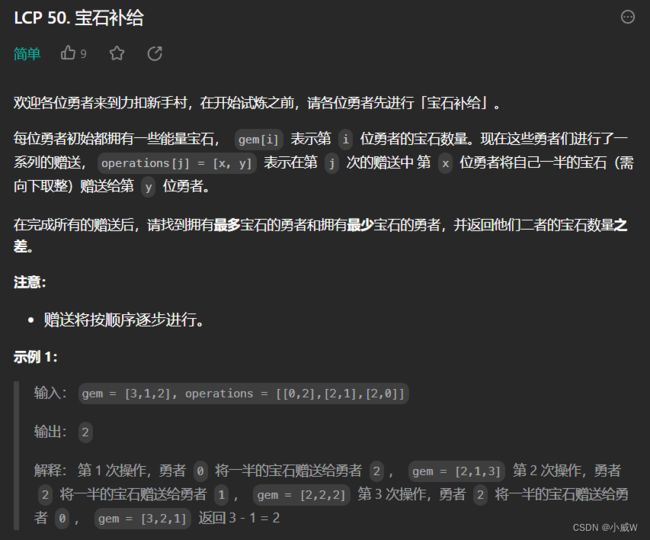
LCP 50. 宝石补给（简单模拟）

https://leetcode.cn/problems/WHnhjV/?envType=daily-question&envId=2023-09-15

提示：
2 <= gem.length <= 10^3
0 <= gem[i] <= 10^3
0 <= operations.length <= 10^4
operations[i].length == 2
0 <= operations[i][0], operations[i][1] < gem.length

按照题意模拟即可，注意向下取整的用法。

class Solution {
    public int giveGem(int[] gem, int[][] operations) {
        // 模拟
        for (int[] op: operations) {
            gem[op[1]] += gem[op[0]] / 2;
            gem[op[0]] = (gem[op[0]] + 1) / 2;
        }
        int mn = gem[0], mx = gem[0];
        for (int g: gem) {
            mn = Math.min(mn, g);
            mx = Math.max(mx, g);
        }
        return mx - mn;
    }
}

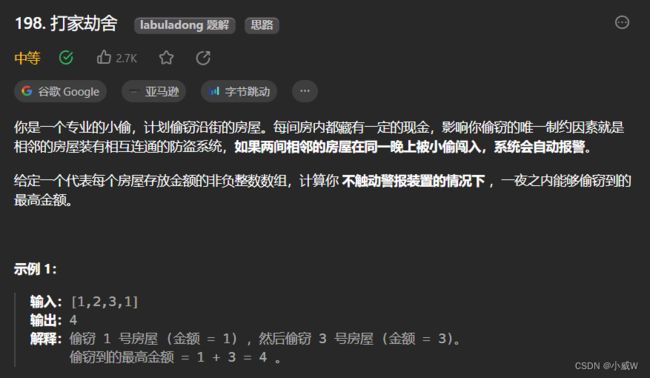
198. 打家劫舍（经典线性DP）

https://leetcode.cn/problems/house-robber/?envType=daily-question&envId=2023-09-16

提示：
1 <= nums.length <= 100
0 <= nums[i] <= 400

经典线性规划嘛——
要么偷当前位置，要么不偷当前位置，取两者最大的。

class Solution {
    public int rob(int[] nums) {
        int n = nums.length;
        if (n == 1) return nums[0];
        int[] dp = new int[n];
        dp[0] = nums[0];
        dp[1] = Math.max(nums[0], nums[1]);
        for (int i = 2; i < n; ++i) dp[i] = Math.max(dp[i - 1], nums[i] + dp[i - 2]);
        return dp[n - 1];
    }
}

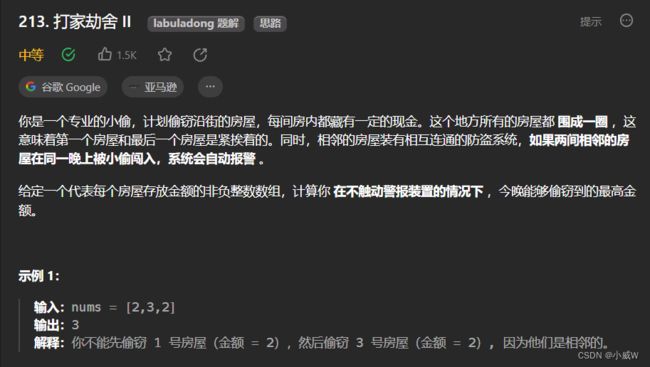
213. 打家劫舍 II（循环打家劫舍）

https://leetcode.cn/problems/house-robber-ii/description/?envType=daily-question&envId=2023-09-17

提示：
1 <= nums.length <= 100
0 <= nums[i] <= 1000

代码写法1——另写方法robR(l, r)

class Solution {
    public int rob(int[] nums) {
        int n = nums.length;
        if (n == 1) return nums[0];
        return Math.max(robR(nums, 0, n - 2), robR(nums, 1, n - 1));
    }

    public int robR(int[] nums, int l, int r) {
        if (l == r) return nums[l];
        int[] dp = new int[r - l + 1];
        dp[0] = nums[l];
        dp[1] = Math.max(dp[0], nums[l + 1]);
        for (int i = l + 2; i <= r; ++i) {
            dp[i - l] = Math.max(dp[i - 1 - l], dp[i - 2 - l] + nums[i]);
        }
        return dp[r - l];
    }
}

代码写法2——二维dp数组

class Solution {
    public int rob(int[] nums) {
        int n = nums.length;
        if (n == 1) return nums[0];
        int[] dp1 = new int[n], dp2 = new int[n];
        dp1[0] = nums[0];
        dp1[1] = Math.max(nums[0], nums[1]);
        dp2[1] = nums[1];
        for (int i = 2; i < n; ++i) {
            dp1[i] = Math.max(dp1[i - 1], dp1[i - 2] + nums[i]);
            dp2[i] = Math.max(dp2[i - 1], dp2[i - 2] + nums[i]);
        }
        return Math.max(dp1[n - 2], dp2[n - 1]);
    }
}

两种写法见仁见智吧。