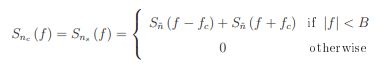通信原理复习笔记（EEEN3005J Communication Theory）(9)
目录
前言
Chapter 13 Power Spectral Density (PSD)
13.1 线性系统的响应（Response of a linear system）
Chapter 14 Noise in Communication Receivers
14.1 热噪声（Thermal Noise）
14.2 过滤噪声 （Filtered Noise）
14.3 窄带噪声的正交分量（Quadrature Components of Narrowband Noise）
前言
本笔记是基于北京都柏林学院2022年EEEN3005J Communication Theory课程课件总结出的笔记。任课教师为Dr Deepu John。
Chapter 13 Power Spectral Density (PSD)
零均值广义平稳随机过程
的自相关函数由下式给出。
此函数具有以下属性：
1、![R_x(0) = E[x^2(t)] = P_x](http://img.e-com-net.com/image/info8/13dc0d28436c42d5ad3503b5761cb7b9.png){kind=small}
是过程的平均功率。
2、
是一个偶数函数，即
功率谱密度（PSD）由下式给出
其中，
是截断信号的傅里叶变换 :
可以证明（省略证明）:
这提供了两种评估过程中平均功率的方法-一种是时间域，一个在频域。
由于
包含正频率和负频率的贡献，因此称为双边PSD
我们可以将单边PSD定义为：
当
可以看出，
表示过程中位于f1和f2之间频带内的功率。
特别是，功率包含在非常小的带宽内
以
为中心的约为
因此被称为“功率谱密度”。
还可以表明，自相关函数和功率谱密度是傅里叶变换对，即：
这就是众所周知的维纳-辛钦定理。
如果对所有
都是常数，那么该过程对所有频率的功率贡献相等，因此被称为“白噪声”。
练习：查找随机加权脉冲序列的PSD
其中：
解决方案（此处未给出）：
所以PSD是白噪声！好耶ヾ(✿ﾟ▽ﾟ)ノ！！！（禁止好耶）
备注：
•我们并没有对
的分布做任何假设，我们只是坚持认为它们是独立的——所以这适用于高斯分布、均匀分布或任何分布。。。
•还要注意，该信号与AWGN噪声看起来非常不同，但它们都具有相同的PSD！！所以PSD并不能告诉我们关于随机过程的一切。
13.1 线性系统的响应（Response of a linear system）
如果将随机过程x（t）作为传递函数H（f）的LTI系统的输入，则输出y（t）也将是随机过程。还可以证明：
如图13.1.2所示，其中系统
为低通滤波器。
Chapter 14 Noise in Communication Receivers
14.1 热噪声（Thermal Noise）
考虑一个电阻R，开路，温度为T（开尔文）。
理想电阻器的端子之间的电压为零，即对于所有时间t,
。
实际电阻器包含大量电子，所有电子都是随机运动的。平均而言，电子均匀分布在整个电阻器中-一端的电子密度不应高于另一端，因此平均终端电压为零：
然而，电子密度存在局部的短期变化。这些会导致端子电压v（t）发生微小变化。
热力学分析得出均方电压为:
其中：
• k = Boltzmann’s constant, 1.38 × 10−23J/C
• T是绝对温度，通常为290K
• B是系统或测量的带宽（Hz）。
我们可以将该噪声电阻器建模为噪声电压源v（t），与理想电阻R串联（见图14.1.1）。
在通信接收机中，负载通常是匹配的，这意味着
。因此
，因此传递给负载的噪声功率是
。
因此，根据方程式（14.1.1），该耗散功率的平均值（或预期值）为![P = E[v^2(t)/4R] = kTB](http://img.e-com-net.com/image/info8/a19c6837378f4f54b916dfe26072ef53.png){kind=small}
。
该最大耗散功率称为可用噪声功率，与电阻R的值无关。
注意，可用功率与带宽B成正比，因此我们说噪声的功率谱密度为
Watts/Hz.
热噪声电压
是具有以下特性的随机过程：
• 广义平稳-平均值和自相关函数不随时间变化
• 遍历-时间平均值趋向于平均值和自相关函数
• 高斯-过程样本具有高斯概率密度函数（这是由于中心极限定理）
• 零平均值-电子在一个方向上没有长期漂移
• 恒定功率谱密度
，其中-噪声功率均匀分布在整个频谱上，称为白噪声。
请注意，实际上，PSD并非在所有频率上都是恒定的，而是在高频下下降。这是因为实际电阻器有一些杂散（寄生）电感和电容，形成低通滤波器，限制了高频带宽。然而，白噪声模型在通信理论中仍然是一个很好的模型。
通过叠加，将噪声添加到接收信号中，称为加性高斯白噪声（AWGN）；如图14.1.2所示。
14.2 过滤噪声 （Filtered Noise）
通信系统使用有限带宽的信号运行。
接收机通常包括一个带通滤波器，该滤波器只通过信号带宽
内的频率-我们称之为滤波器
。
因此，在信道中添加的任何噪声都将在到达解调器之前进行过滤。
如前所述，用w（t）表示宽带噪声，用Sw（f）表示其功率谱密度
这为我们提供了滤波器输出处噪声的PSD表达式。
在调制信号接收机中，相对于中心（载波）频率fc，信号带宽通常非常小。因此，解调器输入处的滤波噪声相对于其中心频率也具有小带宽2B，并且被称为窄带噪声。
如果滤波器输入处的噪声为白色，两侧PSD为
，
所以窄带噪声中的功率是:
假设接收滤波器不是实滤波器，而是一个理想的带通滤波器，在宽度为BN的通带上具有单位增益。那么窄带噪声功率将是:
基于这种比较，我们通过以下公式定义滤波器的噪声等效带宽：
因此，带宽BN上的理想带通滤波器的输出噪声功率与传递函数为的实际滤波器相同。
14.3 窄带噪声的正交分量（Quadrature Components of Narrowband Noise）
由于带通滤波白噪声
是箭头带噪声信号，因此可以用以下形式表示
其中
和
是的正交分量。正交分量具有以下特性：
• 和是统计上相同的基带随机过程，带宽为B
• 和为零均值和高斯分布
• 和为广义静止
• 每个正交分量的功率与原始噪声过程中的功率相同，即。
• 每个正交分量的PSD相同，并且与原始噪声过程的PSD相关
