LeetCode刷题笔记【32】：动态规划专题-4（二维背包问题、一维背包问题、分割等和子集）

动态规划前置知识

参考前文

参考文章：
LeetCode刷题笔记【29】：动态规划专题-1（斐波那契数、爬楼梯、使用最小花费爬楼梯）
LeetCode刷题笔记【30】：动态规划专题-2（不同路径、不同路径 II）
LeetCode刷题笔记【31】：动态规划专题-3（整数拆分、不同的二叉搜索树）

背包问题前置知识

什么是背包问题, 背包问题举例

背包问题的典型案例如下:

有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i]
每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

以上是对背包问题的直白描述, 但是在实际刷题过程中大概率不会这样出题(甚至LeetCode官方也没有"背包问题"这道题)
所以实际应用中, 需要将一般问题转化为背包问题来求解(如今天的第三道例题)

背包问题的大致分类

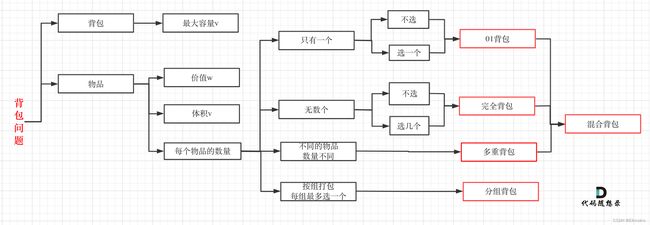
如上图所示, 详细的背包问题分类大概会有 01背包, 完全背包, 多重背包, 分组背包.
但是实际面试中, 最多就考到01背包和完全背包, 更多的就是竞赛水平的题目了.

01背包

就像上面的那个举例, 每一个物品只且只有一个;

所以对于每个物品而言, 只有不放进背包(0)和放进背包(1)两种状态, 所以是"01背包"

完全背包

完全背包问题由01背包问题转化而来, 与之不同的是, 完全背包问题中, 每个物品的数量是无限的

背包问题的通用解法

虽然也可以用回溯遍历的方法, 尝试每个物品"放入/不放入"的所有情况, 但那样的时间复杂度就是指数级的;
故背包问题的最优解法是动态规划算法;

所以说: 背包问题的本质还是动态规划问题
今天三道例题的前两道就将使用类似的动态规划思路, 解决典型的01背包问题.

二维背包问题

题目描述

解题思路

1 构建dp数组

既然是动态规划, 那么我们就来构建一个如上图所示的二维dp数组;

即vector dp(物品数量, vector(背包容量+1, 0))

dp数组中每一格的意义是:
dp[i][j]表示: 在面对容量为j的背包, 以及物品0~i时, 我所能获得的最大收益

2 初始化dp数组

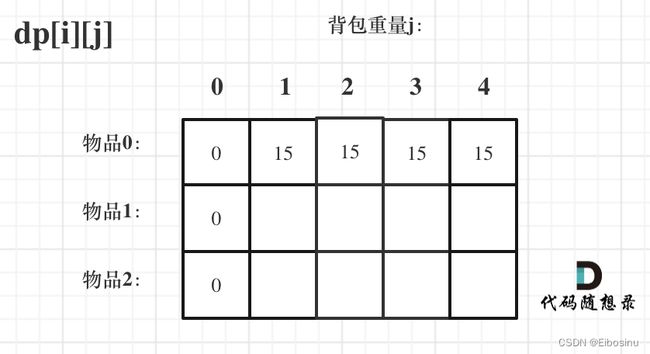
那么首先可以理解上图中为什么这样进行dp数组的初始化, 因为当j太小, 放不下物品0, 收益为0, 放得下以后, 收益为value[0];
代码为:

for(int j=物品0的重量; j<背包容量; ++j){
	dp[0][j] = 物品0的收益;
}

而后进行dp数组的遍历更新

3 遍历更新dp数组

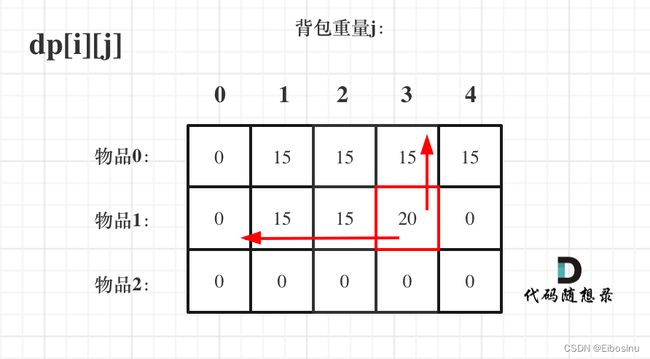
我们以对物品1这一行的更新为例, 对dp[1][0], dp[1][1], dp[1][2]的值应该没什么异议, 因为此时j<3, 还没有到物品1的重量(3), 所以只能照抄上一行的数值(即只放入物品0)

关键是对dp[1][3]和dp[1][4], 也就是说, 在背包的容量可以容纳物品1后, 我们怎么做出选择, 来让当前收益最大.
也就是如何拟定递推公式

符合直觉的思路是: 在放入物品1和不放入物品1中选max, 即max(不放入物品1的收益, 放入物品1的收益)
不放入物品1的收益, 很明显就是上一行的值照抄, 即dp[0][j]
而放入物品1的收益就复杂一些, 因为要考虑到放入物品1后, 剩余的背包空间如何使用才能获得最大收益

(这动态规划的小味儿是不是挠儿的一下就上来了~~)

很明显, 放入物品1后的剩余空间的最大收益, 就是上一行中的dp[0][j-weight[1]]
所以放入物品1的收益=物品1本身的收益+剩余空间的收益, 就是dp[1][j] = value[1] + dp[0][j-weight[1]]

把上面这一系列推导综合一下, 并且从物品1推导到物品i, 就可得到以下代码:

for(int i=1; i<物品数量; ++i){//遍历除了物品0以外的其他物品
	for(int j=0; j<=背包容量; ++j){//遍历所有背包容量的情况
		if(j<weight[i]{//如果背包大小都放不下物品i
			dp[i][j] = dp[i-1][j];//那么就只能照抄上一行
		}else{//如果背包的大小放得下物品i
			dp[i][j] = max(dp[i-1][j], value[i]+dp[i-1][j-weight[i]);//权衡一下不放/放物品i的收益
			// 放物品i的收益 = 物品i本身的收益 + 放物品i后剩余空间所能产生的最大收益
		}
	}
}

代码

int main()
{
    int bagSize = 4;
    vector<int> weight = { 1, 3, 4 };
    vector<int> value = { 15, 20, 30 };
    vector<vector<int>> dp(weight.size(), vector<int>(bagSize + 1, 0));
    // 初始化
    for (int j = 0; j <= bagSize; ++j) {
        if (j >= weight[0]) {
            dp[0][j] = value[0];
        }
    }
    // 遍历
    for (int i = 1; i < weight.size(); ++i) {
        for (int j = 1; j <= bagSize; ++j) {
            if (j < weight[i]) {
                dp[i][j] = dp[i - 1][j];
            }
            else {
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
            }
        }
    }
    cout << dp.back().back();
}

一维背包问题

题目描述

还是和第一题一样的题目, 但是我们这次使用一维dp数组, 用更低的空间复杂度来解题.

解题思路

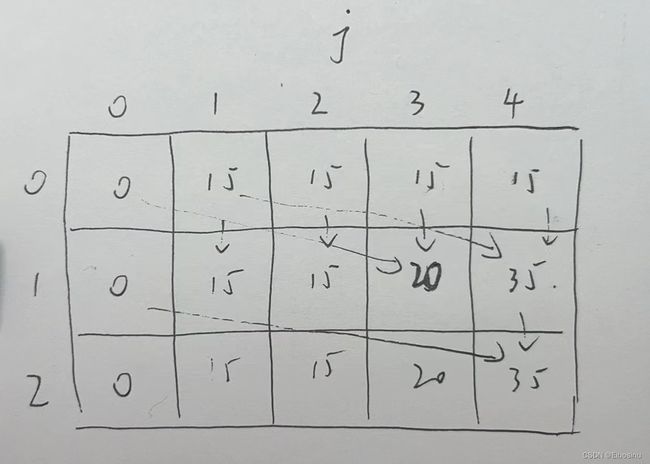
从上图中我们可以看出: 更新遍历的过程, 就是参照上一行的内容(严格来说是上一行左上方的内容), 来填充当前行中内容的过程.

那我们其实不用我维护一整个二维dp数组, 只需要维持原先二维dp数组中的一行(一维dp数组(滚动数组)), 然后更新其中的内容就行了.

那么递推公式就是: dp[j] = max(dp[j], value[i] + dp[j-weight[i]])
代码如下:

for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagSize; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], value[i] + dp[j - weight[i]]);
    }
}

我们发现: 这个遍历更新的过程, 和刚才二维dp数组中, 初始化的过程基本一样, 那我们可不可以将初始化和遍历更新过程合并起来呢?
是可以的, 但是要注意遍历每一行的顺序是反的(即从bagSize到weight[j]), 因为如果从weight[j]到bagSize遍历, 会出现对物品0多次使用的问题, 而题目要求每个物品只能使用一次.

代码

// 以上使用二维的动态规划dp数组解决背包问题
// 但是可以发现: 遍历更新dp数组的过程, 其实就是"根据上一行的内容生成这一行的内容"
// 所以本质上可以使用一维dp数组(一行), 来实现遍历过程
int main()
{
    // 基本信息
    int bagSize = 4;
    vector<int> weight = { 1, 3, 4 };
    vector<int> value = { 15, 20, 30 };
    // 初始化
    vector<int> dp(bagSize + 1, 0);
    // 遍历
    for (int i = 0; i < weight.size(); ++i) {
        for (int j = bagSize; j >= weight[i]; --j) {
            dp[j] = max(dp[j], value[i] + dp[j - weight[i]]);
        }
    }
    cout << dp.back();
}
// 和之前的二维dp数组相比, 一维dp数组的解法中, 一方面遍历顺序是从后往前遍历(避免重复处理的问题);
// 另一方面不需要单独初始化第一行了, 可以在遍历过程中初始化

416. 分割等和子集

题目描述

LeetCode链接：https://leetcode.cn/problems/partition-equal-subset-sum/description/

解题思路

本身题目的描述, 相当于让我们挑出两组数, 让每组的和相等, 如果用回溯暴力解题是很复杂的, 时间复杂度也会很高.

可以将其转化为背包问题:
先求所有数字num的和sum, 将sum/2作为target;
因为每个数字都只能使用一次, 那么问题就转化为01背包问题, 即bagSize=target, 物品i的weight[i]和value[i]都是nums[i], 能否得到一种组合, 可以正好装满容量为target的背包 (即bagSize=target时, 最大收益为target).

代码

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sum=0;
        for(int num : nums)
            sum += num;
        if(sum % 2 == 1)
            return false;
        target = sum/2;
        vector<int> dp(target  + 1, 0);
        for(int i=0; i<nums.size(); ++i){
            for(int j=target ; j>=nums[i]; --j){
                dp[j] = max(dp[j], dp[j-nums[i]]+nums[i]);
            }
        }
        if(dp[target]==target)
            return true;
        else
            return false;
    }
};

总结

这一篇笔记可以说是最近写的最详细认真的一篇了, 背包问题的思路确实十分巧妙;
在掌握了背包问题本身的套路以后, 难点或许就是"如何将其他问题转化为背包问题";
这就要在后续的学习中进一步磨炼了.

本文参考：
二维背包问题
一维背包问题
分割等和子集