线索二叉树——找前驱、后继
前言
一个二叉树被线索化之后,一个节点的前驱或后继会存在两种情况,
1、tag=1,有明确的线索化前驱或后继,
2、tag=0,只存在左右孩子,但是没用明确的线索化前驱后继,需要分析
//线索二叉树结点定义
typedef struct ThreadNode{
int data;
struct ThreadNode *lchild,*rchild;
int ltag,rtag;
}ThreadNode,*ThreadBiTree;1.1、中序线索二叉树找其中序后继
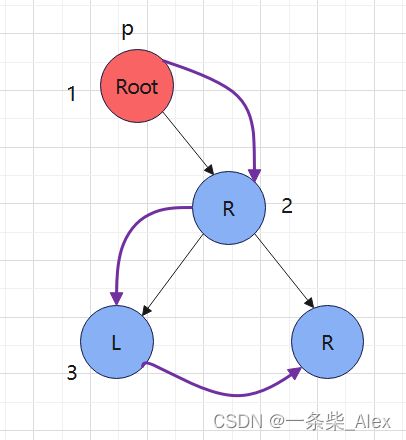
将该二叉树进行中序线索化:
如果想获取任意一个节点p的后继,分析情况如下:
我们将一个二叉树最小化模型:
结点p在L 和R位其实求其前驱或后继,都是可以通过其 lchild和rchild指针直接获取的,
因为它是叶子结点,在进行线索化的时候,已经规定,
1、若 p无右孩子,p->rtag=1,让p的 rchild 指针指向它的 后继
2、若 p无右孩子,p->ltag=1,让p的 lchild 指针指向它的 前驱
因此,我们实际分析的场景是p作为非叶子结点出现的场景:
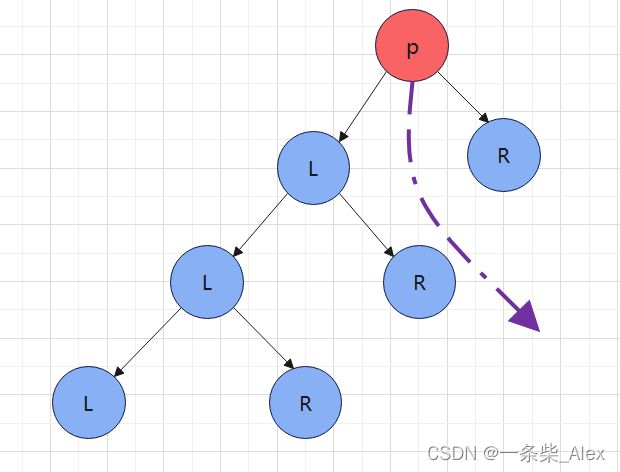
p的中序后继走势:
左、p、右
左、p、(左、根、右)
左、p、((左、根、右) 、根、右)
。。。
也就是说,它的后继趋势是,在p结点的右子树上,不断的向左找,
所以得出一个结论:
p的中序后继=p的右子树最左结点
代码如下:
//中序线索二叉树找后继
//找到以p为根的子树中,第一个被中序遍历的的结点,
ThreadNode * FirstNode(ThreadNode *p){
while(p->ltag==0){
p=p->lchild; //一路向左,但最左节点不一定是叶子结点,具体看下图
return p;
}
}
//在中序线索二叉树中找到结点p的后继结点
ThreadNode *NextNode(ThreadNode *p){
if(p->rtag==0){
return FirstNode(p); //找到其右子树的最左结点
}else
return p->rchild;
}
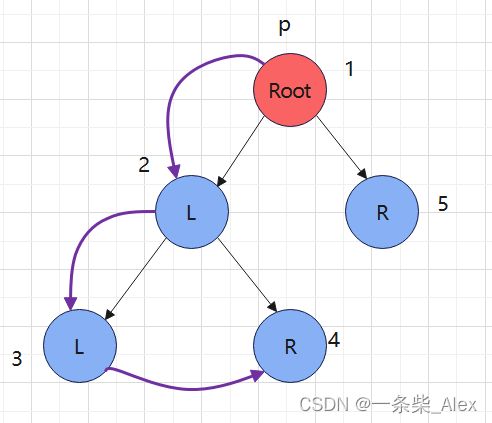
代码中提到的,最左结点不一定是叶子结点的情况:
可以利用中序线索二叉树,查找后继的方法,来对其进行遍历。
线索化之后,遍历的空间复杂度也随之降低,原本中序遍历是通过递归,递归的一次调用,就要压入方法栈一次。但是现在方法栈中只需要压入一个函数即可。
void visit_TBNode(ThreadNode p){
std::cout<<"Node -- "<1.2、中序线索二叉树找其中序前驱
分析过程同上:
P->ltag=1,p->lchild直接指向它的中序前驱,
重点分析p->ltag =0,即p存在左子树的情况:
左、P、右
(左、根、右)、P、右
((左、根、右)、根、右)、P、右
。。。
结论
p的前驱=左子树的最右结点
代码如下:
ThreadNode * LastNode(ThreadNode *p){
while(p->rtag==0){
p=p->rchild;
return p;
}
}
//在中序线索二叉树中找到结点p的前驱结点
ThreadNode *PreNode(ThreadNode *p){
if(p->ltag==0){
return LastNode(p); //找到其右子树的最左结点
}else
return p->rchild;
}
//中序逆序遍历(先定位到以root为根的中序线索树的最后一个节点,然后不断找前驱)
void Rev_InOrder_ThreadBiTree(ThreadBiTree &root){
for(ThreadNode * p= LastNode(root);root!=NULL; PreNode(p)){
visit_TBNode(*p);
}
}
2.1、先序线索二叉树求结点后继
分析:
若要求前序遍历结果中 结点p的前序后继,分析如下:
1、p->rtag=1,则无右孩子,p的前序后继 p->rchild
2、若p->rtag=0 ,p存在右孩子:进一步分析
情况1:若p存在左子树,p的后继为它的左孩子结点
情况2:若p没有左子树,则p的后继为它的右孩子结点
前序遍历顺序:
根、左、右
p、左、右
无论左右子树怎么扩展,最终发现:
1、如果有左子树:(紫色的是遍历路径)
p、左、右
p、(r、左、右)、右
p 、(r、(r、左、右)、右)、右
。。。。
**PS: r 是p左孩子结点,在p的左子树中,它作为根结点出现
存在左子树时,p结点的前驱一定是它的左孩子结点;
1、如果没有左子树:(紫色的是遍历路径)
p、右
p、(r、左、右)
p 、(r、(r、左、右)、右)
。。。。
**PS: r 是p的右孩子结点,在p的右子树中,它作为根结点出现
存在左子树时,p结点的前驱一定是它的右孩子结点;
/**
* 先序线索二叉树找后继
*
* 若要求前序遍历结果中 结点p的前序后继,分析如下:
* 1、p->rtag=1,则无右孩子,p的前序后继 p->rchild
* 2、若p->rtag=0 ,p存在右孩子:进一步分析
* 情况1:若p存在左子树,p的后继为它的左孩子结点
* 情况2:若p没有左子树,则p的后继为它的右孩子结点
*/
//求结点p的前序线索后继
ThreadNode *NextNode_PreOrder(ThreadNode *p) {
if (p->rtag == 0) { //有右子树
return p->lchild != NULL ? p->lchild : p->rchild;
} else
return p->rchild;
}
//由于先序遍历的第一个节点必然是根结点,可以进行如下的先序遍历
void PreOrder_ThreadBiTree_traverse(ThreadBiTree &root) {
for (ThreadNode *p = root; p != NULL; NextNode_PreOrder(p)) {
visit_TBNode(*p);
}
}2.2、先序线索二叉树求结点前驱
若要求前序遍历结果中 结点p的前序线索前驱,分析如下: 1、p->ltag=1,结点p的先序线索前驱为 p->lchild 2、若p->ltag=0,此时是无法得到一个节点的 先序线索前驱的,因为不管怎么样,都是根、左、右的顺序遍历,p点的左右子树都在其后出现 只能通过从 这棵树的根节点用递归的方式,遍历全树,得到p前驱的结果,或者使用三叉链表,在二叉树的结构体定义中加入一个parent 指针,指向自己的父节点。
3.1 后序线索二叉树求结点的前驱
/**
* 后序线索二叉树 求结点的前驱
*
* 分析:
* 1、p->ltag=1, 前驱为 p->lchild
* 2、p->ltag=0,
* 若 p有右孩子 , 前驱为右孩子结点
* 若p没用右孩子,前驱为左孩子
*/
ThreadNode *PreNode_LastOrder(ThreadNode* p){
if(p->ltag==0){
return p->rchild!=NULL?p->rchild:p->lchild;
}else
return p->lchild;
}
//后序线索遍历的逆序 (后序遍历,根结点一定是最后出现的结点)
void Rev_LastOrder_ThreadBiTree_traverse(ThreadBiTree &root) {
for(ThreadNode *p =root;p!=NULL; PreNode_LastOrder(p)){
visit_TBNode(*p);
}
}
3.2 后序线索二叉树求结点的后继
参考2.2