线性代数基础-矩阵
八、矩阵的基础概念
1.矩阵
我们忘掉之前行列式的一切,列一种全新的数表,虽然长得很像,但是大不相同,首先一个区别就是矩阵不能展开成一个值,这里不讨论矩阵的空间意义
{ a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 + . . . + a 2 n x n = b 2 . . . a n 1 x 1 + a n 2 x 2 + a n 3 x 3 + . . . + a n n x n = b n \begin{cases} a_{11}x_1 + a_{12}x_2+a_{13}x_3 +... +a_{1n}x_n= b_1 \\ a_{21}x_1 + a_{22}x_2+a_{23}x_3 +... +a_{2n}x_n= b_2 \\ ...\\ a_{n1}x_1 + a_{n2}x_2+a_{n3}x_3 +... +a_{nn}x_n= b_n \end{cases} ⎩ ⎨ ⎧a11x1+a12x2+a13x3+...+a1nxn=b1a21x1+a22x2+a23x3+...+a2nxn=b2...an1x1+an2x2+an3x3+...+annxn=bn
2.实矩阵、复矩阵
如果矩阵里全是实数,则是实矩阵,而元素是复数,是复矩阵
3.矩阵相等
行数列数相同,所有元素一一对应相等,记作
A = B A=B A=B
4.零矩阵
所有元素全为0,记作
O m ∗ n 或 O O_{m*n} 或O Om∗n或O
5.负矩阵
对于 A m ∗ n ,它的负矩阵是 − A , 相当于矩阵内每个元素乘 ( − 1 ) 对于A_{m*n},它的负矩阵是 -A ,相当于矩阵内每个元素乘(-1) 对于Am∗n,它的负矩阵是−A,相当于矩阵内每个元素乘(−1)
A 3 ∗ 3 = ( a 0 0 0 a 0 0 0 a ) A_{3*3} =\begin{pmatrix} a & 0&0\\ 0 &a&0\\ 0&0&a\\ \end{pmatrix} A3∗3= a000a000a
− A 3 ∗ 3 = ( − a 0 0 0 − a 0 0 0 − a ) -A_{3*3} = \begin{pmatrix} -a & 0&0\\ 0 &-a&0\\ 0&0&-a\\ \end{pmatrix} −A3∗3= −a000−a000−a
6.n阶方阵
矩阵不一定是方的,但是如果是方的就叫方阵,行数或者列数就是阶数
7.三角矩阵,对角矩阵
要求是方阵
上三角,下三角矩阵与上三角下三角行列式定义相同,可以类比
对角矩阵也与行列式相同
A 3 ∗ 3 = ( a b b 0 a b 0 0 a ) A_{3*3} =\begin{pmatrix} a & b&b\\ 0 &a&b\\ 0&0&a\\ \end{pmatrix} A3∗3= a00ba0bba
8.数量矩阵
前提是对角矩阵
主对角线全等于同一个常数a
A 3 ∗ 3 = ( a 0 0 0 a 0 0 0 a ) A_{3*3} =\begin{pmatrix} a & 0&0\\ 0 &a&0\\ 0&0&a\\ \end{pmatrix} A3∗3= a000a000a
9.n阶单位矩阵
主对角线值全为1的矩阵
A 3 ∗ 3 = ( 1 0 0 0 1 0 0 0 1 ) A_{3*3} =\begin{pmatrix} 1 & 0&0\\ 0 &1&0\\ 0&0&1\\ \end{pmatrix} A3∗3= 100010001
10.行矩阵、列矩阵
只有一行或者一列的矩阵
也可以叫行向量,列向量
九、矩阵的线性运算
矩阵的加法和数乘统称为矩阵的线性运算
1.矩阵加法
A_{3*3} =\begin{pmatrix}
a_{11} & a_{12}&a_{13}\
a_{21} & a_{22}&a_{23}\
a_{31} & a_{32}&a_{33}\
\end{pmatrix}
B_{3*3} =\begin{pmatrix}
b_{11} & b_{12}&b_{13}\
b_{21} & b_{22}&b_{23}\
b_{31} & b_{32}&b_{33}\
\end{pmatrix}
A_{33} + B_{33} =
\begin{pmatrix}
a_{11}+b_{11} & a_{12}+b_{12}&a_{13}+b_{13}\
a_{21}+b_{21} & a_{22}+b_{22}&a_{23}+b_{23}\
a_{31}+b_{31}& a_{32}+b_{32}&a_{33}+b_{33}\
\end{pmatrix}
2.交换率
A + B = B + A A +B = B+ A A+B=B+A
3.结合率
( A + B ) + C = A + ( B + C ) (A+B)+C = A+(B+C) (A+B)+C=A+(B+C)
4.特殊运算
A + O = A A + ( − A ) = O A+ O = A\\ A+ (-A) = O A+O=AA+(−A)=O
5.数量乘法
A m ∗ n = ( a 11 a 12 a 13 . . . a 1 n a 21 a 22 a 23 . . . a 2 n . . . . . . . . . . . . . . . a n 1 a n 2 . . . . . . a n n ) A_{m*n} =\begin{pmatrix} a_{11} & a_{12} &a_{13}&...&a_{1n}\\ a_{21} & a_{22}&a_{23}&...&a_{2n}\\ ...&...&...&...&...\\ a_{n1}&a_{n2}&...&...&a_{nn}\\ \end{pmatrix} Am∗n= a11a21...an1a12a22...an2a13a23..................a1na2n...ann
λ ∗ A m ∗ n = ( λ a 11 λ a 12 . . . λ a 1 n λ a 21 λ a 22 . . . λ a 2 n . . . . . . . . . . . . λ a n 1 λ a n 2 . . . λ a n n ) \lambda *A_{m*n} =\begin{pmatrix} \lambda a_{11} & \lambda a_{12} &...& \lambda a_{1n}\\ \lambda a_{21} & \lambda a_{22}&...& \lambda a_{2n}\\ ...&...&...&...\\ \lambda a_{n1}& \lambda a_{n2}&...& \lambda a_{nn}\\ \end{pmatrix} λ∗Am∗n= λa11λa21...λan1λa12λa22...λan2............λa1nλa2n...λann
十、矩阵的乘法
对于每个矩阵乘法,一定有以下规则
A i ∗ k ∗ B k ∗ j = C i ∗ j A{i*k} * B{k * j} = C{i*j} Ai∗k∗Bk∗j=Ci∗j
矩阵乘法的前提是A矩阵的列数,必须等于B的行数,得到新矩阵的行数为A的行数,列数为B的列数。
1.现实记忆法(多存在于国内教材)
把A矩阵的四个行比作四个班级,每一行分别是对三种产品的需求数量
而B矩阵的每一列,他们认为是不同的商家,列中的元素正好是价格
A 4 ∗ 3 = ( a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 a 41 a 42 a 43 ) ( 每行存储的是每个班级对几种产品的需求数量 ) A_{4*3} =\begin{pmatrix} a_{11} & a_{12}&a_{13}\\ a_{21} & a_{22}&a_{23}\\ a_{31} & a_{32}&a_{33}\\ a_{41} & a_{42}&a_{43}\\ \end{pmatrix} (每行存储的是每个班级对几种产品的需求数量) A4∗3= a11a21a31a41a12a22a32a42a13a23a33a43 (每行存储的是每个班级对几种产品的需求数量)
B 3 ∗ 2 = ( b 11 b 12 b 21 b 22 b 31 b 32 ) ( 每列存储的是每个商家几种产品的价格 ) B_{3*2} =\begin{pmatrix} b_{11} & b_{12}\\ b_{21} & b_{22}\\ b_{31} & b_{32}\\ \end{pmatrix} (每列存储的是每个商家几种产品的价格) B3∗2= b11b21b31b12b22b32 (每列存储的是每个商家几种产品的价格)
C 4 ∗ 2 = A 4 ∗ 3 ∗ B 3 ∗ 2 = ( a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 a 41 a 42 a 43 ) ∗ ( b 11 b 12 b 21 b 22 b 31 b 32 ) C_{4*2} = A_{4*3} * B_{3*2} =\begin{pmatrix} a_{11} & a_{12}&a_{13}\\ a_{21} & a_{22}&a_{23}\\ a_{31} & a_{32}&a_{33}\\ a_{41} & a_{42}&a_{43}\\ \end{pmatrix}*\begin{pmatrix} b_{11} & b_{12}\\ b_{21} & b_{22}\\ b_{31} & b_{32}\\ \end{pmatrix} C4∗2=A4∗3∗B3∗2= a11a21a31a41a12a22a32a42a13a23a33a43 ∗ b11b21b31b12b22b32
得到的是一个每个班级在每个商家购买完所需商品的总花销表
C 4 ∗ 2 = ( a 11 ∗ b 11 + a 12 ∗ b 21 + a 13 ∗ b 31 a 11 ∗ b 12 + a 12 ∗ b 22 + a 13 ∗ b 32 a 21 ∗ b 11 + a 22 ∗ b 21 + a 23 ∗ b 31 a 21 ∗ b 12 + a 22 ∗ b 22 + a 23 ∗ b 32 a 31 ∗ b 11 + a 32 ∗ b 21 + a 33 ∗ b 31 a 31 ∗ b 12 + a 32 ∗ b 22 + a 33 ∗ b 32 a 41 ∗ b 11 + a 42 ∗ b 21 + a 43 ∗ b 31 a 41 ∗ b 12 + a 42 ∗ b 22 + a 43 ∗ b 32 ) C_{4*2} =\begin{pmatrix} a_{11}*b_{11}+a_{12}*b_{21} +a_{13}*b_{31}& a_{11}*b_{12}+a_{12}*b_{22} +a_{13}*b_{32}\\ a_{21}*b_{11}+a_{22}*b_{21} +a_{23}*b_{31} & a_{21}*b_{12}+a_{22}*b_{22} +a_{23}*b_{32} \\ a_{31}*b_{11}+a_{32}*b_{21} +a_{33}*b_{31}& a_{31}*b_{12}+a_{32}*b_{22} +a_{33}*b_{32}\\ a_{41}*b_{11}+a_{42}*b_{21} +a_{43}*b_{31} &a_{41}*b_{12}+a_{42}*b_{22} +a_{43}*b_{32}\\ \end{pmatrix} C4∗2= a11∗b11+a12∗b21+a13∗b31a21∗b11+a22∗b21+a23∗b31a31∗b11+a32∗b21+a33∗b31a41∗b11+a42∗b21+a43∗b31a11∗b12+a12∗b22+a13∗b32a21∗b12+a22∗b22+a23∗b32a31∗b12+a32∗b22+a33∗b32a41∗b12+a42∗b22+a43∗b32
公式比较复杂,相当于这个过程
- A的第一行分别对应乘B的第一列,写到C的第一列
- A的第二行分别对应乘B的第一列,写到C的第一列
- A的第三行分别对应乘B的第一列,写到C的第一列
- A的第四行分别对应乘B的第一列,写到C的第一列
- A的第一行分别对应乘B的第二列,写到C的第二列
- A的第二行分别对应乘B的第二列,写到C的第二列
- A的第三行分别对应乘B的第二列,写到C的第二列
- A的第四行分别对应乘B的第二列,写到C的第二列
1. 需要注意乘法的前提条件:A的列数 = B的行数
2. AB是A左乘B,也可以是B右乘A,AB与BA结果不同
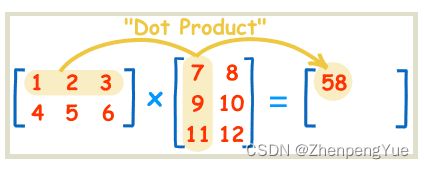
2.另一种记忆方法
我们以更简单的矩阵举例:
A 2 ∗ 2 = ( 1 2 2 3 ) A_{2*2} =\begin{pmatrix} 1 &2\\ 2& 3\\ \end{pmatrix} A2∗2=(1223)
B 2 ∗ 1 = ( 1 2 ) B_{2*1} =\begin{pmatrix} 1 \\ 2\\ \end{pmatrix} B2∗1=(12)
很容易得出
C 2 ∗ 1 = A 2 ∗ 2 ∗ B 2 ∗ 1 = ( 1 ∗ 1 + 2 ∗ 2 2 ∗ 1 + 3 ∗ 2 ) = ( 5 8 ) C_{2*1} =A_{2*2} *B_{2*1}=\begin{pmatrix} 1*1+2*2\\ 2*1+3*2\\ \end{pmatrix} = \begin{pmatrix} 5\\ 8\\ \end{pmatrix} C2∗1=A2∗2∗B2∗1=(1∗1+2∗22∗1+3∗2)=(58)
可以理解为这样的一个操作,A第一列*B第一行 + A第二列 * B第二行
C 2 ∗ 1 = A i 1 ∗ B 1 j + A i 2 ∗ B 2 j C_{2*1} = A_{i1}*B_{1j} +A_{i2}* B_{2j} C2∗1=Ai1∗B1j+Ai2∗B2j
我们拓展到更高阶的矩阵
A 3 ∗ 3 = ( 1 2 3 2 3 4 1 4 6 ) A_{3*3} =\begin{pmatrix} 1 &2&3\\ 2& 3&4\\ 1& 4&6\\ \end{pmatrix} A3∗3= 121234346
B 3 ∗ 2 = ( 2 2 1 3 1 2 ) B_{3*2} =\begin{pmatrix} 2 &2\\ 1& 3\\ 1& 2\\ \end{pmatrix} B3∗2= 211232
C 3 ∗ 2 = ( 1 2 3 2 3 4 1 4 6 ) ∗ ( 2 2 1 3 1 2 ) C_{3*2} =\begin{pmatrix} 1 &2&3\\ 2& 3&4\\ 1& 4&6\\ \end{pmatrix} *\begin{pmatrix} 2 &2\\ 1& 3\\ 1& 2\\ \end{pmatrix} C3∗2= 121234346 ∗ 211232
C 3 ∗ 2 = ( 1 2 1 ) ∗ ( 2 2 ) + ( 2 3 4 ) ∗ ( 1 3 ) + ( 3 4 6 ) ∗ ( 1 2 ) C_{3*2} = \begin{pmatrix} 1 \\ 2\\ 1\\ \end{pmatrix} *\begin{pmatrix} 2 &2\\ \end{pmatrix}+\begin{pmatrix} 2 \\ 3\\ 4\\ \end{pmatrix}*\begin{pmatrix} 1&3\\ \end{pmatrix}+\begin{pmatrix} 3 \\ 4\\ 6\\ \end{pmatrix}*\begin{pmatrix} 1 &2\\ \end{pmatrix} C3∗2= 121 ∗(22)+ 234 ∗(13)+ 346 ∗(12)
C 3 ∗ 2 = ( 2 2 4 4 2 2 ) + ( 2 6 3 9 4 12 ) + ( 3 6 4 8 6 12 ) = ( 7 14 11 21 12 26 ) C_{3*2} =\begin{pmatrix} 2&2 \\ 4&4\\ 2&2\\ \end{pmatrix} + \begin{pmatrix} 2&6 \\ 3&9\\ 4&12\\ \end{pmatrix}+ \begin{pmatrix} 3&6 \\ 4&8\\ 6&12\\ \end{pmatrix} = \begin{pmatrix} 7&14 \\ 11&21\\ 12&26\\ \end{pmatrix} C3∗2= 242242 + 2346912 + 3466812 = 71112142126
C 3 ∗ 2 = A i 1 ∗ B 1 j + A i 2 ∗ B 2 j + A i 3 ∗ B 3 j C_{3*2} = A_{i1}*B_{1j} +A_{i2}* B_{2j}+A_{i3}* B_{3j} C3∗2=Ai1∗B1j+Ai2∗B2j+Ai3∗B3j
可以浅显的理解为A的第x列 * B的第x行 的累加求和
十一、矩阵乘法的运算性质
1.结合律
A ( B C ) = ( A B ) C A(BC) = (AB)C A(BC)=(AB)C
2.分配律
A ( B + C ) = A B + A C λ ( A B ) = A ( λ B ) = ( λ A ) B A(B+C) = AB+AC\\ \lambda (AB) = A(\lambda B) = (\lambda A)B A(B+C)=AB+ACλ(AB)=A(λB)=(λA)B
3.与单位阵的运算
E m ∗ A m ∗ n = A m ∗ n ∗ E n = A m ∗ n E_m * A_{m*n} = A_{m*n} *E_n = A_{m*n} Em∗Am∗n=Am∗n∗En=Am∗n
4.可交换
一般情况下 A B = B A 如果 A B = B A ,则称 A 与 B 可换 一般情况下AB \cancel{=} BA\\ 如果AB=BA,则称A与B可换 一般情况下AB= BA如果AB=BA,则称A与B可换
5.转置矩阵
同行列式转置几乎一致(参考行列式转置),记作
A T 或 A ′ A^T 或A' AT或A′
转置之后的矩阵和原矩阵不相等,这里与行列式有差别,有如下性质
( A T ) T = A ( A + B ) T = A T + B T ( λ A ) T = λ A T ( A B ) T = B T A T (A^T )^T = A\\ (A+B)^T = A^T + B^T \\ (\lambda A)^T = \lambda A^T\\ (AB)^T = B^T A^T (AT)T=A(A+B)T=AT+BT(λA)T=λAT(AB)T=BTAT
6.对称矩阵
条件:
- A是n阶方阵
- A的转置 = A
性质:
A 是对称矩阵,则 k 倍的 A 也是对称矩阵 A , B 均是对称矩阵, A + B , A − B 也是对称矩阵 A , B 是对称矩阵, A B = B A , A B 也是对称矩阵 A是对称矩阵,则k倍的A也是对称矩阵 A,B均是对称矩阵,A+B,A-B也是对称矩阵 A,B是对称矩阵,AB=BA,AB也是对称矩阵 A是对称矩阵,则k倍的A也是对称矩阵A,B均是对称矩阵,A+B,A−B也是对称矩阵A,B是对称矩阵,AB=BA,AB也是对称矩阵
7.反对称矩阵
A T = − A A^T = -A AT=−A
性质:主对角线元素全为0
8.n阶方阵的特殊运算
A是N阶方阵,有如下运算
A 0 = E n A n = A A . . . A ( k 个 A ) A k A l = A k + l ( A k ) l = A k l E k = E A^0 = E_n\\ A^n = AA...A(k个A)\\ A^kA^l = A^{k+l}\\ (A^{k})^l = A^{kl}\\ E^k = E A0=EnAn=AA...A(k个A)AkAl=Ak+l(Ak)l=AklEk=E
对于N阶方阵A,B
( A B ) k = A k B k ( A + B ) 2 = A 2 + 2 A B + B 2 (AB)^k \cancel{=} A^kB^k\\ (A+B)^2 \cancel{=} A^2+2AB+B^2 (AB)k= AkBk(A+B)2= A2+2AB+B2
十二、矩阵与行列式
- 只有n阶方阵才有相应行列式,否则没有
- A的行列式记作
∣ A ∣ 或 d e t A |A| 或det A ∣A∣或detA
性质:设A为n阶方阵
∣ A T ∣ = ∣ A ∣ ∣ λ A ∣ = λ n ∣ A ∣ ∣ A B ∣ = ∣ A ∣ ∣ B ∣ |A^T| = |A|\\ |\lambda A| = \lambda ^n |A|\\ |AB| = |A| |B| ∣AT∣=∣A∣∣λA∣=λn∣A∣∣AB∣=∣A∣∣B∣
解释:
- 因为行列式的转置和原来相等,那么转置矩阵变成行列式还是跟原来相等
- 矩阵乘一个常数是所有元素都乘常数,但是行列式乘常数只能乘进一行
- 可以通过数学归纳或者拉普拉斯公式证明
十三、逆矩阵、伴随矩阵、奇异矩阵
1.逆矩阵
A ∗ B = B ∗ A = E n A * B = B*A= E_n A∗B=B∗A=En
则称B为A的逆矩阵,简称逆阵,记作
B = A − 1 B = A^{-1} B=A−1
有如下的性质
A ∗ A − 1 = A − 1 ∗ A = E n A * A^{-1} = A^{-1} *A= E_n A∗A−1=A−1∗A=En
( A − 1 ) − 1 = A A 可逆, A T 也可逆, ( A T ) − 1 = ( A − 1 ) T A 可逆且 k = 0 , 则 k A 可逆 , ( k A ) − 1 = 1 k A − 1 A , B 同阶且可逆,则 A B 也可逆,( A B ) − 1 = B − 1 A − 1 ( 可推广到 n 个 ) 若 A 可逆 , ∣ A − 1 ∣ = ∣ A ∣ − 1 (A^{-1})^{-1} = A\\ A可逆,A^T也可逆,(A^T)^{-1} = (A^{-1})^T\\ A可逆且k \cancel{=}0,则kA可逆,(kA)^{-1 } = \frac{1}{k}A^{-1}\\ A,B同阶且可逆,则AB也可逆,(AB)^{-1}=B^{-1}A^{-1} (可推广到n个)\\ 若A可逆,|A^{-1}| = |A|^{-1} (A−1)−1=AA可逆,AT也可逆,(AT)−1=(A−1)TA可逆且k= 0,则kA可逆,(kA)−1=k1A−1A,B同阶且可逆,则AB也可逆,(AB)−1=B−1A−1(可推广到n个)若A可逆,∣A−1∣=∣A∣−1
2.奇异矩阵与非奇异矩阵
奇异矩阵也叫退化矩阵,非奇异矩阵才可逆,奇异矩阵不可逆
∣ A ∣ ≠ 0 非奇异矩阵 ∣ A ∣ = 0 奇异矩阵 |A| \not= 0 非奇异矩阵\\ |A| =0奇异矩阵 ∣A∣=0非奇异矩阵∣A∣=0奇异矩阵
3.伴随矩阵
A 3 ∗ 3 = ( 1 2 3 2 2 1 3 4 3 ) A_{3*3} =\begin{pmatrix} 1 & 2&3\\ 2 &2&1\\ 3&4&3\\ \end{pmatrix} A3∗3= 123224313
还记得代数余子式吗,划掉所在行列的行列式,乘-1^(i+j)
Astar就等于对每个矩阵的位置求一个代数余子式的值,然后放在矩阵的同位置
4.伴随矩阵求逆矩阵
充要条件:
∣ A ∣ ≠ 0 , A − 1 = 1 ∣ A ∣ A ∗ |A| \not=0,A^{-1} = \frac{1}{|A|} A^* ∣A∣=0,A−1=∣A∣1A∗
推论:
A B = E ,则 A , B 互为逆 AB = E,则A,B互为逆 AB=E,则A,B互为逆
十四、矩阵的初等变换
1.初等变换
我们还是把矩阵想象为方程组,方程组能干的,矩阵就能这么做
{ a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 + . . . + a 2 n x n = b 2 . . . a n 1 x 1 + a n 2 x 2 + a n 3 x 3 + . . . + a n n x n = b n \begin{cases} a_{11}x_1 + a_{12}x_2+a_{13}x_3 +... +a_{1n}x_n= b_1 \\ a_{21}x_1 + a_{22}x_2+a_{23}x_3 +... +a_{2n}x_n= b_2 \\ ...\\ a_{n1}x_1 + a_{n2}x_2+a_{n3}x_3 +... +a_{nn}x_n= b_n \end{cases} ⎩ ⎨ ⎧a11x1+a12x2+a13x3+...+a1nxn=b1a21x1+a22x2+a23x3+...+a2nxn=b2...an1x1+an2x2+an3x3+...+annxn=bn
下面三种方式叫做初等行变换
- 交换任意两行
- 任意一行乘k
- 某一行乘k加到另一行
行换成列,就是初等列变换,统称初等变换
2.矩阵等价
若A可以经过若干次初等变换到B,则称A与B等价,记作 A~B
- 具备传递性,A~B ,B~C ,则A~C
- 具备对称性 A~B ,B~A
- 具备反身性,A~A
3.行阶梯矩阵
A 4 ∗ 4 = ( 1 2 3 3 0̸ 3 4 5 0̸ 0̸ 2 1 0̸ 0̸ 0̸ 0̸ ) A_{4*4} =\begin{pmatrix} 1 &2&3&3\\ \not0& 3&4&5\\ \not0& \not0&2&1\\ \not0&\not0&\not0&\not0 \end{pmatrix} A4∗4= 1000230034203510
如果一个矩阵的零行都位于非零行下方,并且每个非零行左起第一个非零元素的列数由上而下严格递增,则称该矩阵为行阶梯矩阵
最简行阶梯矩阵:对于一个行阶梯矩阵,如果每行左起第一个非零元素元素都是1,并且这些1所在的列其他元素都是0,则称最简行阶梯矩阵(行最简形矩阵)
A 4 ∗ 4 = ( 1 0 0 0 0 1 0 0 0 0 1 3 0 0 0 0 ) A_{4*4} =\begin{pmatrix} 1 &0&0&0\\ 0& 1&0&0\\ 0& 0&1&3\\ 0&0&0&0 \end{pmatrix} A4∗4= 1000010000100030
再对A进行初等列变换,得到A的标准型
A 4 ∗ 4 = ( 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 ) A_{4*4} =\begin{pmatrix} 1 &0&0&0\\ 0& 1&0&0\\ 0& 0&1&0\\ 0&0&0&0 \end{pmatrix} A4∗4= 1000010000100000
定义m,n,r,其中mn为行数列数
而该标准型左上角的单位阵可以由r确定,所以三个数就可以表示出标准型
E r = ( 1 0 0 0 1 0 0 0 1 ) E_r = \begin{pmatrix} 1 &0&0\\ 0& 1&0\\ 0& 0&1\\ \end{pmatrix} Er= 100010001
所有与A等价的矩阵组成一个等价类,标准型是这个类中最简单的矩阵
十五、初等矩阵与步骤记录
1.定理
定义:由单位阵E经过一次初等变换形成的矩阵,叫做初等矩阵
定理2:
-
对A(m*n)进行一次初等行变换,相当于在A左侧乘相应的m阶初等矩阵
-
对A(m*n)进行一次初等列变换,相当于在A右侧乘相应的n阶初等矩阵
因为这个定理,我们可以只需要记录下来从A到E变换过程的所有初等矩阵,再对E来一遍,就可以求出A的逆矩阵
2.初等变换法求逆矩阵:
A 3 ∗ 3 = ( 1 1 − 1 3 2 − 2 5 − 2 1 ) A_{3*3} =\begin{pmatrix} 1& 1&-1\\ 3 & 2&-2\\ 5& -2&1\\ \end{pmatrix} A3∗3= 13512−2−1−21
= > ( 1 1 − 1 ∣ 1 0 0 3 2 − 2 ∣ 0 1 0 5 − 2 1 ∣ 0 0 1 ) =>\begin{pmatrix} 1& 1&-1&| & 1&0&0\\ 3 & 2&-2&|&0&1&0\\ 5& -2&1&|&0&0&1\\ \end{pmatrix} => 13512−2−1−21∣∣∣100010001
= > ( 1 0 0 ∣ − 2 1 0 0 1 0 ∣ − 13 6 − 1 0 0 1 ∣ − 16 7 − 1 ) =>\begin{pmatrix} 1& 0&0&| & -2&1&0\\ 0 & 1&0&|&-13&6&-1\\ 0& 0&1&|&-16&7&-1\\ \end{pmatrix} => 100010001∣∣∣−2−13−161670−1−1
3.初等矩阵的性质
性质:
- 初等矩阵都可逆,逆矩阵仍是初等矩阵
- 初等矩阵的转置还是初等矩阵
十六、矩阵的秩
1.k阶子式
在矩阵A中,任取K个行K个列,交叉处的元素不改变相对位置形成的新的k阶行列式
2.矩阵的秩
- 有一个不等于0的 r 阶子式
- 所有 r+1 阶子式等于0
满足这两个条件的子式叫做最高阶非零子式,r称为矩阵的秩
性质:
R ( A ) = R ( A T ) = R ( k A ) ( 常数 k ≠ 0 ) 存在 x 阶子式不为 0 , R ( A ) > = s 所有 t 阶子式为 0 , R ( A ) < t A 为 n 阶方阵, A 为奇异矩阵的充要条件 R ( A ) = n R(A) = R(A^T) = R(kA) (常数k \not=0)\\ 存在x阶子式不为0,R(A)>=s\\ 所有t阶子式为0,R(A)
3.满秩矩阵、降秩矩阵
R(A) = min(m , n) 称为满秩矩阵,否则为降秩矩阵
4.求矩阵的秩
- 按定义
- 初等行变换到行阶梯矩阵,非零行的个数为R的值
5.矩阵秩的性质
A为mn阶矩阵,B为nk阶矩阵
(1).性质1
C ( m + k ) ∗ ( n + l ) = ( A O O B ) C_{(m+k)*(n+l)} =\begin{pmatrix} A& O\\ O & B\\ \end{pmatrix} C(m+k)∗(n+l)=(AOOB)
R ( C ) = R ( A ) + R ( B ) R(C) = R(A) + R(B) R(C)=R(A)+R(B)
(2).性质2
C ( m + k ) ∗ ( n + l ) = ( A O C B ) C_{(m+k)*(n+l)} =\begin{pmatrix} A& O\\ C & B\\ \end{pmatrix} C(m+k)∗(n+l)=(ACOB)
Q ( m + k ) ∗ ( n + l ) = ( A D O B ) Q_{(m+k)*(n+l)} =\begin{pmatrix} A& D\\ O & B\\ \end{pmatrix} Q(m+k)∗(n+l)=(AODB)
R ( C ) > = R ( A ) + R ( B ) R ( Q ) > = R ( A ) + R ( B ) R(C) >=R(A) + R(B)\\ R(Q) >=R(A) + R(B) R(C)>=R(A)+R(B)R(Q)>=R(A)+R(B)
(3).性质3
R ( A ) + R ( B ) < = R ( A + B ) R(A)+R(B)<=R(A+B) R(A)+R(B)<=R(A+B)
(4).性质4
R ( A B ) < = m i n { R ( A ) , R ( b ) } R(AB)<=min\{R(A),R(b)\} R(AB)<=min{R(A),R(b)}
(5).性质5
R ( A ) + R ( B ) − n < = R ( A B ) R(A)+R(B)-n<=R(AB) R(A)+R(B)−n<=R(AB)
(6).性质6
A B = O , R ( A ) + R ( B ) < n AB = O,R(A)+R(B)
十七、分块矩阵

分块矩阵就是随意切成n块,然后再算
它把子矩阵作为元素,运算性质和矩阵相同
分块对角矩阵:若 A i A_i Ai都是方阵,则A称为对角分块矩阵
A 3 ∗ 3 = ( A 1 A 2 . . . A s ) A_{3*3} =\begin{pmatrix} A_1& &\\ & A_2&\\ & &...&\\ & &&A_s\\ \end{pmatrix} A3∗3= A1A2...As
尽量选择良好的分块,可以提高效率
A 3 ∗ 3 = ( 9 0 0 0 2 1 0 0 0 0 3 4 0 0 0 2 ) = ( 9 0 ∣ 0 0 2 1 ∣ 0 0 − − − − − 0 0 ∣ 3 4 0 0 ∣ 0 2 ) A_{3*3} =\begin{pmatrix} 9& 0&0&0\\ 2&1&0&0\\ 0&0 &3&4\\ 0& 0&0&2\\ \end{pmatrix} = \begin{pmatrix} 9& 0&|&0&0\\ 2&1&|&0&0\\ -&-&-&-&-\\ 0&0 &|&3&4\\ 0& 0&|&0&2\\ \end{pmatrix} A3∗3= 9200010000300042 = 92−0001−00∣∣−∣∣00−3000−42
十八、线性方程组
1.非齐次线性方程组
{ a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 + . . . + a 2 n x n = b 2 . . . a n 1 x 1 + a n 2 x 2 + a n 3 x 3 + . . . + a n n x n = b n \begin{cases} a_{11}x_1 + a_{12}x_2+a_{13}x_3 +... +a_{1n}x_n= b_1 \\ a_{21}x_1 + a_{22}x_2+a_{23}x_3 +... +a_{2n}x_n= b_2 \\ ...\\ a_{n1}x_1 + a_{n2}x_2+a_{n3}x_3 +... +a_{nn}x_n= b_n \end{cases} ⎩ ⎨ ⎧a11x1+a12x2+a13x3+...+a1nxn=b1a21x1+a22x2+a23x3+...+a2nxn=b2...an1x1+an2x2+an3x3+...+annxn=bn
2.齐次线性方程组
{ a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = 0 a 21 x 1 + a 22 x 2 + a 23 x 3 + . . . + a 2 n x n = 0 . . . a n 1 x 1 + a n 2 x 2 + a n 3 x 3 + . . . + a n n x n = 0 \begin{cases} a_{11}x_1 + a_{12}x_2+a_{13}x_3 +... +a_{1n}x_n= 0 \\ a_{21}x_1 + a_{22}x_2+a_{23}x_3 +... +a_{2n}x_n= 0 \\ ...\\ a_{n1}x_1 + a_{n2}x_2+a_{n3}x_3 +... +a_{nn}x_n=0 \end{cases} ⎩ ⎨ ⎧a11x1+a12x2+a13x3+...+a1nxn=0a21x1+a22x2+a23x3+...+a2nxn=0...an1x1+an2x2+an3x3+...+annxn=0
简单来看就是b全是0的非齐次
3.系数矩阵与增广矩阵
A x = b x 称为未知数向量, b 为常数项向量 A x = b\\ x称为未知数向量,b为常数项向量 Ax=bx称为未知数向量,b为常数项向量
有一个方程组,如下
{ a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 + . . . + a 2 n x n = b 2 . . . a n 1 x 1 + a n 2 x 2 + a n 3 x 3 + . . . + a n n x n = b n \begin{cases} a_{11}x_1 + a_{12}x_2+a_{13}x_3 +... +a_{1n}x_n= b_1 \\ a_{21}x_1 + a_{22}x_2+a_{23}x_3 +... +a_{2n}x_n= b_2 \\ ...\\ a_{n1}x_1 + a_{n2}x_2+a_{n3}x_3 +... +a_{nn}x_n= b_n \end{cases} ⎩ ⎨ ⎧a11x1+a12x2+a13x3+...+a1nxn=b1a21x1+a22x2+a23x3+...+a2nxn=b2...an1x1+an2x2+an3x3+...+annxn=bn
该方程组的系数矩阵为:
A m ∗ n = ( a 11 a 12 a 13 . . . a 1 n a 21 a 22 a 23 . . . a 2 n a 31 a 32 a 33 . . . a 3 n . . . . . . . . . . . . . . . . . . . . . . . . . . . a ( n − 1 ) n a n 1 a n 2 . . . a n ( n − 1 ) a n n ) A_{m*n} =\begin{pmatrix} a_{11} & a_{12} &a_{13}&...&a_{1n}\\ a_{21} & a_{22}&a_{23}&...&a_{2n}\\ a_{31}&a_{32}&a_{33}&...&a_{3n}\\ ...&...&...&...&...\\ ...&...&...&...&a_{(n-1)n}\\ a_{n1}&a_{n2}&...&a_{n(n-1)}&a_{nn}\\ \end{pmatrix} Am∗n= a11a21a31......an1a12a22a32......an2a13a23a33........................an(n−1)a1na2na3n...a(n−1)nann
该方程组的增广矩阵为:
A ~ m ∗ n = ( a 11 a 12 a 13 . . . a 1 n b 1 a 21 a 22 a 23 . . . a 2 n b 2 a 31 a 32 a 33 . . . a 3 n b 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . a ( n − 1 ) n b n − 1 a n 1 a n 2 . . . a n ( n − 1 ) a n n b n ) \widetilde{A}_{m*n} =\begin{pmatrix} a_{11} & a_{12} &a_{13}&...&a_{1n}&b_1\\ a_{21} & a_{22}&a_{23}&...&a_{2n}&b_2\\ a_{31}&a_{32}&a_{33}&...&a_{3n}&b_3\\ ...&...&...&...&...\\ ...&...&...&...&a_{(n-1)n}&b_{n-1}\\ a_{n1}&a_{n2}&...&a_{n(n-1)}&a_{nn}&b_n\\ \end{pmatrix} A m∗n= a11a21a31......an1a12a22a32......an2a13a23a33........................an(n−1)a1na2na3n...a(n−1)nannb1b2b3bn−1bn
4.线性方程组的解
满足线性方程组的一组数x1 =k1,x2 = k2…,叫做线性方程组的解或者特解
写成向量形式,叫做线性方程组的解向量,记作
x = ( k 1 , k 2 , . . . k n ) T x = (k_1,k_2,...k_n)^T x=(k1,k2,...kn)T
全体解向量的集合叫做解集,求解集的过程叫解线性方程组
如果两个线性方程组结集相同,称他们为同解线性方程组
表达线性方程组全部解的表达式,称为通解
5.高斯消元法解线性方程组
求解非齐次线性方程组 { x 1 − 2 x 2 + 3 x 3 − x 4 = 1 3 x 1 − x 2 + 5 x 3 − 3 x 4 = 2 2 x 1 + x 2 + 2 x 3 − 2 x 4 = 3 求解非齐次线性方程组\begin{cases} x_1 -2 x_2+3x_3 -x_4= 1 \\ 3x_1 - x_2+5x_3 -3x_4= 2 \\ 2x_1 +x_2+2x_3 -2x_4=3 \end{cases} 求解非齐次线性方程组⎩ ⎨ ⎧x1−2x2+3x3−x4=13x1−x2+5x3−3x4=22x1+x2+2x3−2x4=3
A ~ = ( 1 − 2 3 − 1 ∣ 1 3 − 1 5 − 3 ∣ − 1 2 1 2 − 2 ∣ − 2 ) = > ( 1 − 2 3 − 1 ∣ 1 0 5 − 4 0 ∣ − 1 0 0 0 0 ∣ − 2 ) = B ~ \widetilde A =\begin{pmatrix} 1 & -2&3&-1&|&1\\ 3 & -1&5&-3&|&-1\\ 2&1&2&-2&|&-2\\ \end{pmatrix} = >\begin{pmatrix} 1 & -2&3&-1&|&1\\ 0& 5&-4&0&|&-1\\ 0&0&0&0&|&-2\\ \end{pmatrix} = \widetilde B A = 132−2−11352−1−3−2∣∣∣1−1−2 => 100−2503−40−100∣∣∣1−1−2 =B
{ x 1 = 1 + 2 x 2 − 3 x 3 + x 4 x 2 = ( 2 + 4 x 3 ) / 5 0 = − 2 \begin{cases} x_1 = 1+2 x_2-3x_3 +x_4 \\ x_2=( 2 +4x_3)/5\\ 0=-2 \end{cases} ⎩ ⎨ ⎧x1=1+2x2−3x3+x4x2=(2+4x3)/50=−2
显然第三个方程矛盾,该方程组无解
步骤如下:
- 写出增广矩阵
- 初等行变换为行阶梯矩阵
- 取每行首个非零元素对应x作为因变量
6.线性方程组解与秩的关系
(1)对于齐次/非齐次方程组
R ( A ) < R ( A ~ ) = > 无解 R ( A ) = R = n ( A ~ ) = > 有唯一解 R ( A ) = R < n ( A ~ ) = > 有无穷多解 R(A)
(2)对于齐次方程组
R ( A ) = n = > 有唯一解,只有零解 R ( A ) < n = > 有无穷多解,有非零解 R(A) =n \space \space =>有唯一解,只有零解\\ R(A)
当齐次方程组的系数矩阵为方阵时,行列式为0说明R(A)
1. 任何方阵都可以通过初等行变换转化为上三角阵.
2. 当且仅当主对角线上的元素中有0,上三角阵的行列式为0.
3. n阶上三角阵(行阶梯矩阵)的秩 = n - 主对角线上0的个数.
十九、向量与线性
1.向量
只有一行的矩阵称为行向量,一列的矩阵称为列向量
α = ( 1 2 3 ) , β = ( 1 2 3 ) \alpha = \begin{pmatrix} 1 \\ 2\\ 3 \end{pmatrix},\beta = \begin{pmatrix} 1 &2&3\\ \end{pmatrix} α= 123 ,β=(123)
元素个数n称为维数,而第i个元素称为向量的第i个分量
2.向量组
若干个同维的列(行)向量所组成的集合称为向量组
A n ∗ m = ( α 1 , α 2 , . . . α m ) A_{n*m}=(\alpha_1,\alpha_2,...\alpha_m) An∗m=(α1,α2,...αm)
3.线性组合
对于 A n ∗ m = ( α 1 , α 2 , . . . α m ) ,实数 ( k 1 , k 2 . . . k m ) k 1 α 1 + k 2 α 2 + . . . + k m α m 称为向量组 A 的线性组合 ( k 1 , k 2 . . . k m ) 称为这个向量组的系数 对于A_{n*m}=(\alpha_1,\alpha_2,...\alpha_m),实数(k_1,k_2...k_m)\\ k_1\alpha_1 + k_2\alpha_2 +...+k_m\alpha_m称为向量组A的线性组合\\ (k_1,k_2...k_m)称为这个向量组的系数 对于An∗m=(α1,α2,...αm),实数(k1,k2...km)k1α1+k2α2+...+kmαm称为向量组A的线性组合(k1,k2...km)称为这个向量组的系数
简单来说,就是把里面的向量随便乘一堆非线性的常量系数加一起,就是线性组合
4.线性表示
如果A的通过线性组合,能表示出β,我们称β是向量组A的线性组合,或者β可以被A线性表示
如果有A,B两个向量组,B中每个向量都能被A线性表示,称向量组B可以被A线性表示
若A,B可以相互线性表示,则记作A~B,AB等价
β 可以被 A 线性表示 < = > R ( A ) = R ( A β ) = m B 可以被 A 表示 < = > R ( A B ) = R ( A ) = > R ( A ) > = R ( B ) A 等价于 B < = > R ( A ) = R ( B ) = R ( A B ) β可以被A线性表示<=>R(A) = R(A \space \space β) = m\\ B可以被A表示 <=> R(A\space \space B) = R(A)=>R(A)>=R(B)\\ A 等价于B <=> R(A) = R(B) = R(A\space \space B) β可以被A线性表示<=>R(A)=R(A β)=mB可以被A表示<=>R(A B)=R(A)=>R(A)>=R(B)A等价于B<=>R(A)=R(B)=R(A B)
5.线性相关
对于 A n ∗ m = ( α 1 , α 2 , . . . α m ) ,存在实数 ( k 1 , k 2 . . . k m ) 使 k 1 α 1 + k 2 α 2 + . . . + k m α m = 0 则称 A 线性相关,否则称 A 线性无关 对于A_{n*m}=(\alpha_1,\alpha_2,...\alpha_m),存在实数(k_1,k_2...k_m)\\ 使k_1\alpha_1 + k_2\alpha_2 +...+k_m\alpha_m = 0\\ 则称A线性相关,否则称A线性无关 对于An∗m=(α1,α2,...αm),存在实数(k1,k2...km)使k1α1+k2α2+...+kmαm=0则称A线性相关,否则称A线性无关
对于向量组 A A A而言
A 线性无关 < = > R ( A ) = m A 线性相关 < = > R ( A ) < m A线性无关<=>R(A) = m\\ A线性相关<=>R(A)
-
推论:m个n维向量组成向量组,n
-
推论:包含零向量的向量组一定线性相关
- 注意:若向量组只有一个向量,向量线性相关的充要条件是这个向量为0向量
- 注意:若向量组只有两个向量,线性相关的充要条件是共线,三个共面
-
定理6:若A中至少有一个向量可以由其他向量表示<=>A线性相关
-
定理7:A线性无关,而向量组(A β)线性相关,则β可以被A唯一表示
-
定理8:A中有部分向量线性相关,则A线性相关,A线性无关,任意部分向量线性无关
-
定理9:若A能被B线性表示,且A的向量数量比B多,A线性相关
- 推论:A可由B线性表示,A线性无关,则A的元素数不多于B
6.极大无关组
(1)定义:
在向量组A中,能找出r个向量,满足
- r个向量线性无关
- 任意r+1个向量线性相关
简单理解就是找一组元素数量最多的线性无关的向量,能表示A中任意向量,我们称这个向量组为 A 0 A_0 A0
A 0 A_0 A0就是向量组A的一个最大的无关向量组,称极大无关组,向量个数r称为向量组A的秩
注意:
-
只含零向量的向量组没用极大无关组,规定秩为0
-
线性无关向量组的极大无关组是本身
-
一般向量组的极大无关组不唯一,元素个数相等,相互等价
-
定理10:向量组与它的极大无关组等价
-
定理11:若A中存在r阶子式不等于0,则这个子式所在r个列向量线性无关
若所有r阶子式为0,则任意r个向量线性相关 -
定理12:向量组的秩等于向量组组成的矩阵的秩,某个r阶子式非零,则这个子式所在r个列向量是A的极大无关组
二十、方程组解的结构
1.齐次方程
性质: β 1 , β 2 β1 ,β2 β1,β2 是 A x = 0 Ax = 0 Ax=0的两个解,那么 k 1 β 1 + k 2 β 2 k1β1 + k2β2 k1β1+k2β2也是它的解
定义:
若 β 1 , β 2 , . . . β n β1,β2,...βn β1,β2,...βn线性无关
Ax=0的任意解可以被 β 1 , β 2 , . . . β n β1,β2,...βn β1,β2,...βn表示出来
我们称 β 1 , β 2 , . . . β n β1,β2,...βn β1,β2,...βn为 A x = 0 Ax =0 Ax=0的基础解系
定理13:
如果齐次方程有非零解,一定有基础解系,且基础解系解向量个数=n-r
r为系数矩阵A的秩,n为未知量个数,n-r是自由未知量个数
通解 x = k 1 + β 1 + k 2 β 2 + . . . + k n β n x = k1+β1+k2β2+...+knβn x=k1+β1+k2β2+...+knβn
2.非齐次方程
性质2:β1 ,β2 是 A x = b Ax = b Ax=b的两个解,那么β1 - β2是Ax=0的解
性质3: η是 A x = b Ax=b Ax=b的解,β是 A x = 0 Ax=0 Ax=0的解,则 η + β η+β η+β是 A x = b Ax=b Ax=b的解
定理14:若 η ∗ η* η∗ 是 A x = b Ax=b Ax=b的一个特解, A x = 0 Ax=0 Ax=0的基础解为 β 1 , . . . β n − r β1,...βn-r β1,...βn−r
则通解 x = η ∗ + β 1 + β n − r x = η* + β1+βn-r x=η∗+β1+βn−r