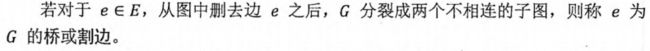图论学习-无向图双连通分量

无向图双连通分量

1.基本术语与概念

给定一个无向图G = (V,E):

1.1.割点

1.2.桥

例：

1.3.边双连通分量 (e-DCC)

极大的不含有桥的连通块被称为边双连通分量。
图中的两个边双连通分量之间一定有桥
每个桥至少属于两个边双连通分量

1.4 点双连通分量 (v-DCC)

极大的不包含割点的连通块被称为点双连通分量。
每个割点至少属于两个点双连通分量。
图中的两个点双连通分量之间一定有割点

1.5 时间戳

类似有向图的时间戳
dfn[x]：记录dfs时的搜索顺序，第一次访问x的编号
low[x]：记录x所能到达的编号最小的点

2.求解

2.1 边双连通分量

2.1.1 如何找到桥？

y无论如何也走不到x，y最高只能走到它自己，那么x和y的这条边就是桥。
容易发现：如果y能够走到x或者走到x的祖宗节点，即当low[y]>=dfn[x]时，x和y的这条边一定不是桥，因为x和y在一个环里。

2.1.2 如何找所有边的双连通分量？

方法一：把所有桥删掉
方法二：用栈维护，当有dfn[x]==low[x]时，说明x是当前双连通分量的最高点，x的父节点和x之前的边就是一座桥，此时栈里的所有点就是一个边双连通分量。

2.1.3 例题 P2860 [USACO06JAN]Redundant Paths G

给定一个无向连通图，问最少加几条边，使得图中任意两点之间至少包含两条相互分离的路径。
链接
转换题意：给定一个无向连通图，问最少加几条边，可以将其变成一个边双连通分量。

对于转换题意的证明：
要证明：
边双连通分量等价于图中任意两点之间至少包含两条相互分离的路径。

首先边双连通分量：不含桥
必要性：边双连通分量不含桥显然有至少两条相互分离的路径

充分性：那么如何证明图中任意两点之间都至少包含两条相互分离的路径，那么就是这个图就是一个边双连通分量。

给出充分性的证明：
反证法：假设，任意两点之间都至少包含两条相互分离的路径，且此图不是一个边双连通分量。
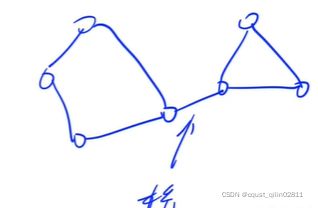
那么该图至少存在一个桥，使得去掉这个桥之后，桥的两边不连通，如果在桥的左右边各选一个点，那么这两个点是不可到达的。显然矛盾。
所以充分性得证。

对于必要性，画图验证是感觉是对的，但是证明不太好证。

尝试给出必要性的证明：
首先图是一个边双连通分量
那么对于图中任意两点至少有两条相互分离的路径，如何证明？
反证法：假设该图中存在两点只有一条相互分离的路径，那么把这条路径上的任选一条边删除，那么就变成了两个不连通的子图，显然这条路径上的任意一条边都是桥，而边双连通分量不含桥，与定义矛盾。
所以得证。
y总原话：《当成结论来记》

边双连通分量等价于：对于图中任意两点，一定存在两条相互分离的路径。

继续解决问题：最少加几条边，可以将其变成一个边双连通分量。
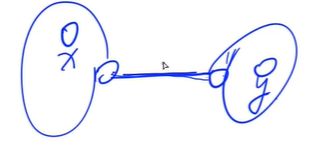
尝试对图中所有边双连通分量进行缩点，缩完点后一定是一棵树，这是显然的。
可以看看图加以理解：

那么要把一棵树变成边双连通分量，显然要对这棵树所有度数为1的点都加上一条边：

（加边方式不唯一）
$$\begin{gathered} 设度数为1的点的个数为cnt \\ 那么最少需要加\lfloor \frac{cnt+1}{2}\rfloor 条边能使得 \\ 该树成为一个边连通分量 \end{gathered}$$
优先让度数为1的点互相连接，如果还剩有度数为1的点未连接，把它连接任意一个点即可。易有：
$$\begin{gathered} 当cnt为偶数时，答案是\frac{cnt}{2} \\ 当cnt为奇数时，答案是\frac{cnt}{2}+1 \\ 合并有\lfloor \frac{cnt+1}{2}\rfloor \\ 注：y总原话：当成结论来记:) \end{gathered}$$
例图：

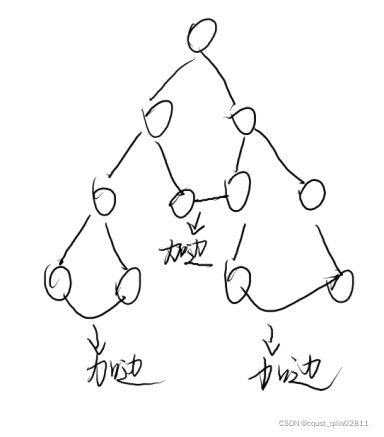
注：最好是相邻的度数为1的点相连
如果不相邻，会有这种特例：
像下图这样加边就是不行的：

代码实现：

#include
using namespace std;

const int N = 5010,M = 20010;
int n,m;
int h[N],e[M],ne[M],idx;
int dfn[N],low[N],timestamp;
int stk[N],top;
int id[N],dcc_cnt;
bool is_bridge[M];
int d[N];
void add(int a,int b)
{
    e[idx] = b,ne[idx] = h[a],h[a] = idx++;
}
void tarjan(int u, int from)
{
    dfn[u] = low[u] = ++ timestamp;
    stk[ ++ top] = u;
    
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (!dfn[j])
        {
            tarjan(j, i);
            low[u] = min(low[u], low[j]);
            if (dfn[u] < low[j])
                is_bridge[i] = is_bridge[i ^ 1] = true;
        }
        else if (i != (from ^ 1))
            low[u] = min(low[u], dfn[j]);
    }
    
    if (dfn[u] == low[u])
    {
        ++ dcc_cnt;
        int y;
        do {
            y = stk[top -- ];
            id[y] = dcc_cnt;
        } while (y != u);
    }
}

int main()
{
    cin>>n>>m;
    memset(h, -1, sizeof h);
    while (m -- ){
        int a,b;
        cin>>a>>b;
        add(a,b),add(b,a);
    }
    tarjan(1,-1);
    for(int i = 0;i<idx;i++)
    {
        if(is_bridge[i])
        {
            d[id[e[i]]]++;
        }
    }
    int cnt = 0;
    for(int i = 1;i<=dcc_cnt;i++)
    {
        if(d[i]==1)
            cnt++;
    }
    cout<<(cnt+1)/2;
    return 0;
}

2.2 点双连通分量

2.2.1 如何求割点？

类似于找桥，如何判断x是否是割点？
对于x和y，low[y]必须大于等于dfn[x]，因为如果low[y]小于dfn[x]，说明y可以搜到x的上面，那么x和y必然在一个环内，可以相互到达。
两种情况：

1. 如果x不是根节点，只要low[y]>=dfn[x]，那么x必然是割点
2. x是根节点，由割点定义可知，如果x只有一个子节点，说明去除x及x所有连接的边以后，就只有一个子图，不满足割点定义。 所以如果x是根节点，那么x需要有两个子节点，且满足low[y]>=dfn[x]
   所以对于2，只要x是根节点看，那么就计算它的子树的数量，如果它有两棵及以上的子树，那么它就是割点。

2.2.2 步骤：

1. 首先选定一个根节点，从该根节点开始遍历整个图（dfs预处理dfn数组）
2. 对于根节点来说，计算它的子树数量，如果它有两棵及以上的子树，那么它就是割点，因为去掉这个点过后，这两棵子树一定不能互相到达。
3. 对于其他节点，维护的两个数组dfn和low，这两个数组的定义在前面已经说过了，对于图中两点u,v,只要low[u]>=dfn[v],说明u能到的最高点比v还要深，那么v就是割点。

如何计算low[u]是一个问题。
考虑当前顶点为u，那么首先low[u] = dfn[u]，遍历u所能到达的所有的边（u,v）,如果v没有访问过，就访问它，那么访问完v回溯的值low[v]一定是v所能遍历到的最小的点，那么u能到达的最小的点low[u]与low[v]取个最小值，即low[u] = min(low[u],low[v]),最终u的所有邻点遍历完后,low[u]一定是u所能遍历到的编号最小的点，也即是当前它所在连通分量的最高点。

例题

后续更新~

参考资料

acwing算法提高课
算法竞赛进阶指南