周赛335(模拟、质因子分解、分组背包)
题解:0x3f
https://leetcode.cn/problems/number-of-ways-to-earn-points/solution/fen-zu-bei-bao-pythonjavacgo-by-endlessc-ludl/
文章目录
- 周赛335
-
- [6307. 递枕头](https://leetcode.cn/problems/pass-the-pillow/)
-
- 模拟
- [6308. 二叉树中的第 K 大层和](https://leetcode.cn/problems/kth-largest-sum-in-a-binary-tree/)
- [2584. 分割数组使乘积互质](https://leetcode.cn/problems/split-the-array-to-make-coprime-products/)
-
- 质因子分解+区间合并
- [2585. 获得分数的方法数](https://leetcode.cn/problems/number-of-ways-to-earn-points/)
-
- 分组背包
周赛335
6307. 递枕头
难度简单4
n 个人站成一排,按从 1 到 n 编号。
最初,排在队首的第一个人拿着一个枕头。每秒钟,拿着枕头的人会将枕头传递给队伍中的下一个人。一旦枕头到达队首或队尾,传递方向就会改变,队伍会继续沿相反方向传递枕头。
- 例如,当枕头到达第
n个人时,TA 会将枕头传递给第n - 1个人,然后传递给第n - 2个人,依此类推。
给你两个正整数 n 和 time ,返回 time 秒后拿着枕头的人的编号。
示例 1:
输入:n = 4, time = 5
输出:2
解释:队伍中枕头的传递情况为:1 -> 2 -> 3 -> 4 -> 3 -> 2 。
5 秒后,枕头传递到第 2 个人手中。
示例 2:
输入:n = 3, time = 2
输出:3
解释:队伍中枕头的传递情况为:1 -> 2 -> 3 。
2 秒后,枕头传递到第 3 个人手中。
提示:
2 <= n <= 10001 <= time <= 1000
模拟
class Solution {
public int passThePillow(int n, int time) {
n = n-1;
boolean rev = false;
while(time > n){
time -= n;
rev = !rev;
}
return rev ? (n-time+1) : time+1;
}
}
6308. 二叉树中的第 K 大层和
难度中等1
给你一棵二叉树的根节点 root 和一个正整数 k 。
树中的 层和 是指 同一层 上节点值的总和。
返回树中第 k 大的层和(不一定不同)。如果树少于 k 层,则返回 -1 。
注意,如果两个节点与根节点的距离相同,则认为它们在同一层。
示例 1:
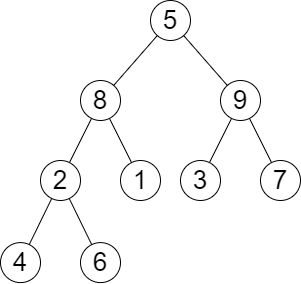
输入:root = [5,8,9,2,1,3,7,4,6], k = 2
输出:13
解释:树中每一层的层和分别是:
- Level 1: 5
- Level 2: 8 + 9 = 17
- Level 3: 2 + 1 + 3 + 7 = 13
- Level 4: 4 + 6 = 10
第 2 大的层和等于 13 。
示例 2:
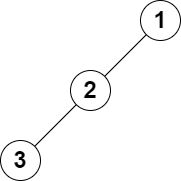
输入:root = [1,2,null,3], k = 1
输出:3
解释:最大的层和是 3 。
提示:
- 树中的节点数为
n 2 <= n <= 1051 <= Node.val <= 1061 <= k <= n
class Solution {
public long kthLargestLevelSum(TreeNode root, int k) {
PriorityQueue<Long> pq = new PriorityQueue<>();
if(root == null) return -1;
Deque<TreeNode> dq = new ArrayDeque<>();
dq.addLast(root);
while(!dq.isEmpty()){
int size = dq.size();
long sum = 0;
while(size-- > 0){
TreeNode cur = dq.pollFirst();
sum += cur.val;
if(cur.left != null) dq.addLast(cur.left);
if(cur.right != null) dq.addLast(cur.right);
}
if(pq.size() < k) pq.add(sum);
else{
if(pq.peek() < sum){
pq.remove();
pq.add(sum);
}
}
}
return pq.size() < k ? -1 : pq.peek();
}
}
2584. 分割数组使乘积互质
难度中等17
给你一个长度为 n 的整数数组 nums ,下标从 0 开始。
如果在下标 i 处 分割 数组,其中 0 <= i <= n - 2 ,使前 i + 1 个元素的乘积和剩余元素的乘积互质,则认为该分割 有效 。
- 例如,如果
nums = [2, 3, 3],那么在下标i = 0处的分割有效,因为2和9互质,而在下标i = 1处的分割无效,因为6和3不互质。在下标i = 2处的分割也无效,因为i == n - 1。
返回可以有效分割数组的最小下标 i ,如果不存在有效分割,则返回 -1 。
当且仅当 gcd(val1, val2) == 1 成立时,val1 和 val2 这两个值才是互质的,其中 gcd(val1, val2) 表示 val1 和 val2 的最大公约数。
示例 1:
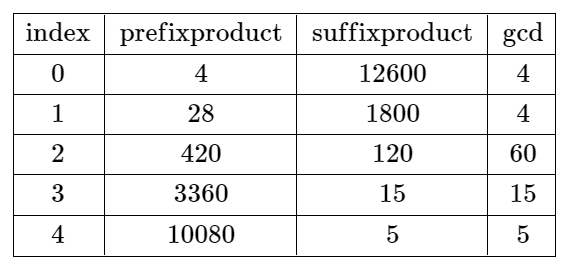
输入:nums = [4,7,8,15,3,5]
输出:2
解释:上表展示了每个下标 i 处的前 i + 1 个元素的乘积、剩余元素的乘积和它们的最大公约数的值。
唯一一个有效分割位于下标 2 。
示例 2:
输入:nums = [4,7,15,8,3,5]
输出:-1
解释:上表展示了每个下标 i 处的前 i + 1 个元素的乘积、剩余元素的乘积和它们的最大公约数的值。
不存在有效分割。
提示:
n == nums.length1 <= n <= 1041 <= nums[i] <= 106
质因子分解+区间合并
class Solution {
// 互质:左半部分和右半部分没有公共的质因子
// 逆向思维:哪些地方不能分割 ==> 区间合并问题
// 如何分解质因子?
public int findValidSplit(int[] nums) {
int n = nums.length;
Map<Integer, Integer> left = new HashMap<Integer, Integer>(); // left[p] 表示质数 p 首次出现的下标
int[] right = new int[n]; // right[i] 表示左端点为 i 的区间的右端点的最大值
for (int i = 0; i < n; i++) {
int x = nums[i];
for (int d = 2; d * d <= x; ++d) // 分解质因数
if (x % d == 0) {
if (left.containsKey(d))
right[left.get(d)] = i; // 记录左端点对应的右端点的最大值
else
left.put(d, i); // 第一次遇到质数 d
for (x /= d; x % d == 0; x /= d) ;
}
if (x > 1) // 找到了一个质因子 x
if (left.containsKey(x))
right[left.get(x)] = i;
else
left.put(x, i);
}
for(int l = 0, maxR = 0; l < n; l++){
if(l > maxR){// 最远可以遇到 maxR
return maxR;
}
maxR = Math.max(maxR, right[l]);
}
return -1;
}
}
2585. 获得分数的方法数
难度困难11
考试中有 n 种类型的题目。给你一个整数 target 和一个下标从 0 开始的二维整数数组 types ,其中 types[i] = [counti, marksi] 表示第 i 种类型的题目有 counti 道,每道题目对应 marksi 分。
返回你在考试中恰好得到 target 分的方法数。由于答案可能很大,结果需要对 109 +7 取余。
注意,同类型题目无法区分。
- 比如说,如果有
3道同类型题目,那么解答第1和第2道题目与解答第1和第3道题目或者第2和第3道题目是相同的。
示例 1:
输入:target = 6, types = [[6,1],[3,2],[2,3]]
输出:7
解释:要获得 6 分,你可以选择以下七种方法之一:
- 解决 6 道第 0 种类型的题目:1 + 1 + 1 + 1 + 1 + 1 = 6
- 解决 4 道第 0 种类型的题目和 1 道第 1 种类型的题目:1 + 1 + 1 + 1 + 2 = 6
- 解决 2 道第 0 种类型的题目和 2 道第 1 种类型的题目:1 + 1 + 2 + 2 = 6
- 解决 3 道第 0 种类型的题目和 1 道第 2 种类型的题目:1 + 1 + 1 + 3 = 6
- 解决 1 道第 0 种类型的题目、1 道第 1 种类型的题目和 1 道第 2 种类型的题目:1 + 2 + 3 = 6
- 解决 3 道第 1 种类型的题目:2 + 2 + 2 = 6
- 解决 2 道第 2 种类型的题目:3 + 3 = 6
示例 2:
输入:target = 5, types = [[50,1],[50,2],[50,5]]
输出:4
解释:要获得 5 分,你可以选择以下四种方法之一:
- 解决 5 道第 0 种类型的题目:1 + 1 + 1 + 1 + 1 = 5
- 解决 3 道第 0 种类型的题目和 1 道第 1 种类型的题目:1 + 1 + 1 + 2 = 5
- 解决 1 道第 0 种类型的题目和 2 道第 1 种类型的题目:1 + 2 + 2 = 5
- 解决 1 道第 2 种类型的题目:5
示例 3:
输入:target = 18, types = [[6,1],[3,2],[2,3]]
输出:1
解释:只有回答所有题目才能获得 18 分。
提示:
1 <= target <= 1000n == types.length1 <= n <= 50types[i].length == 21 <= counti, marksi <= 50
分组背包
class Solution {
private static final int MOD = (int) 1e9 + 7;
public int waysToReachTarget(int target, int[][] types) {
int[] f = new int[target+1];
f[0] = 1;
for(int[] p : types){
int count = p[0], marks = p[1];
for(int j = target; j > 0; j--){
for(int k = 1; k <= count && k <= j / marks; k++){
f[j] = (f[j] + f[j-k*marks]) % MOD;
}
}
}
return f[target];
}
}
int count = p[0], marks = p[1];
for(int j = target; j > 0; j--){
for(int k = 1; k <= count && k <= j / marks; k++){
f[j] = (f[j] + f[j-k*marks]) % MOD;
}
}
}
return f[target];
}
}