《META KNOWLEDGE CONDENSATION FOR FEDERATED LEARNING》

论文阅读《META KNOWLEDGE CONDENSATION FOR FEDERATED LEARNING》

挺有槽点的一篇论文，公式的符号感觉挺乱的，细节也没有交代清楚，而且方法堆砌得有点多。

全文简介

作者说，现在的联邦学习都是交换模型参数，但是，这会在服务器和多个客户机之间产生严重的通信负担。于是作者引入了元知识的方式，从分布式客户端中提取元知识，直接上传元知识给服务器，让服务器在云知识上训练就行了。随着训练的进行，训练样本对联邦模型的贡献也会发生变化。因此，坐着引入了一个动态的权重分配机制，使样本能够自适应地对当前的模型更新做出贡献。在组合的元知识上训练模型，而不在不同的客户之间暴露原始数据，可以显著减轻异构问题。此外，为了进一步改善数据的异构性，我们还在客户端之间交换元知识作为局部元知识提取的条件初始化。

主要就是几点：

1. 客户端通过本地数据计算出元数据，上传元数据代替模型参数。
2. 服务器收到客户端提交的元数据后进行训练，提出了一种动态的权重分配方案来提高元知识的信息量，得到新的全局模型。以及一种知识共享策略来在不泄露原始数据的情况下在客户间交换元知识。
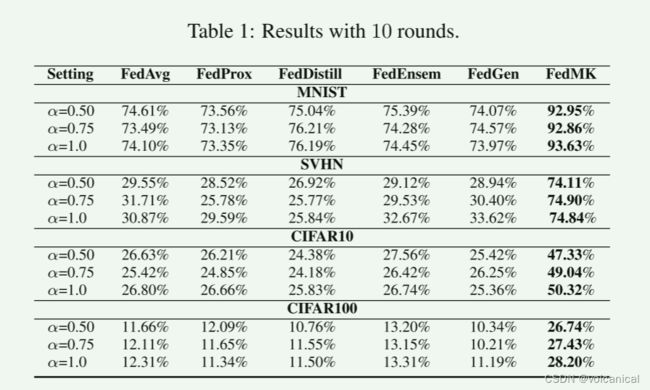
3. 引入了一个服务器端条件生成器来对上传的元知识的统计分布进行建模，以稳定训练过程。得益于提取的元知识和学习的统计分布，模型比竞争方法需要更少的沟通轮，同时获得更好的性能。

1. 获取元知识

1.1 元知识提取

具体方法可见：
Aravind Rajeswaran, Chelsea Finn, Sham M Kakade, and Sergey Levine. Meta-learning with implicit gradients.
In NeurIPS, 2019.
和
Dataset distillation.

$${\hat{\mathcal{D}}}^c=\underset{{\mathcal{D}}^c}{\mathrm{argmin}}{\mathcal{L}}^c\left({\mathbf{w}}^{\ast },{\mathcal{D}}^c\right)\text{ s.t. }{\mathbf{w}}^{\ast }=\underset{{\mathbf{w}}^c}{\mathrm{argmin}}{\mathcal{L}}^c\left({\mathbf{w}}^c,{\hat{\mathcal{D}}}^c\right)$$
通过优化以上目标获得客户端上的元知识${\mathcal{D}}^c$

1.2 权重划分

使用每一个样本的损失的函数作为样本权重，显然，在当前模型中，每个样本的权重与其预测损失成反比。
$${\varphi }_i^c=\frac{1}{1+\exp (-\tau \ast \ell \left({\mathbf{w}}^c,x_i^c,y_i^c\right)}$$
我们为每个样本分配权重，以更新元知识:
$${\hat{\mathcal{D}}}^c\leftarrow {\hat{\mathcal{D}}}^c-\alpha \nabla {\mathcal{L}}^c\left({\mathbf{w}}^c,{\Phi }^c\circ {\mathcal{D}}^c\right),$$

1.3 元知识共享

每一轮，每个客户端的初始元知识是另一个客户端上一轮的元知识，即从别人的元知识初始化，然后训练。作者说这样可以解决异质性的问题。

2. 服务器训练

因为客户端直接上传元数据，那么这时候服务器就可以训练一个GAN，来学习获得客户端上传数据的分布，对于GAN的训练过程这里不作介绍。
GAN的生成器在训练后可以生成近似于客户端提交上来的元知识的分布，这时候就可以使用生成器来生成近似良好的元知识。
此时作者不仅仅使用客户端提交上来的元知识，同时使用生成器生成的元知识进行训练，如下式所示：
$${\mathcal{L}}_{\text{overall }}\left({\mathbf{W}}_G,\left\{\hat{\mathcal{D}},{\hat{\mathcal{D}}}^{\text{pseu }}\right\}\right)=\mathcal{L}\left({\mathbf{W}}_G,\hat{\mathcal{D}}\right)+\beta \mathcal{L}\left({\mathbf{W}}_G,{\hat{\mathcal{D}}}^{\text{pseu }}\right),$$
其中$\beta$=$\frac{|{\hat{\mathcal{D}}}^{\text{pseu }}|}{|\hat{\mathcal{D}}|}$.

3. 实验结果

十轮后的准确率结果，说实话，有点难以置信。

4. 算法流程