双向A*算法
前面看最佳路径优先搜索算法的时候顺便研究了一下它的改进算法:双向最佳路径优先搜索算法。那既然有双向最佳路径优先搜索算法自然也可以有双向A* 算法。这篇文章简单看一下双向A*算法的基本原理以及代码实现。
基本原理
双向A* 算法是一种用于解决图搜索问题的启发式搜索算法。它是A* 算法的一种改进,旨在减少搜索的节点数量,从而提高搜索的效率。
双向A*算法同时从起点和终点开始搜索,分别利用启发式函数来评估节点的优先级。在每一步中,从两个方向选择具有最低优先级的节点进行扩展。当两个搜索方向的搜索路径相交时,即找到了一条从起点到终点的路径。
相比于普通的A算法,双向A算法可以显著减少搜索的节点数量,特别是在图搜索问题中,当图的规模较大时,搜索的效率提高得更为明显。它通过同时从起点和终点搜索,利用双向信息来减少不必要的搜索。
其基本思路如下:
1.初始化起点和终点,并分别给它们分配初始的启发式函数值(即估计从起点到终点的距离)。
2.初始化起点和终点的优先级队列,分别用来存放待扩展的节点。
3.从起点和终点同时开始搜索,每次选择优先级最低的节点进行扩展。
4.对于当前被选择的节点,计算并更新它的启发式函数值、代价值(即从起点到该节点的实际路径长度)以及总的估计值(即启发式函数值加上代价值)。
5.在每一次扩展节点时,检查是否有节点在另一个方向上已经被访问过,如果存在交叉节点,则找到一条路径并返回。
6.如果没有交叉节点,继续选择下一个优先级最低的节点进行扩展,直到找到路径或者搜索完所有的节点。
7.如果搜索完所有的节点都没有找到路径,则说明起点和终点之间不存在可达路径。
代码实现
简单实现代码如下:
import os
import sys
import math
import heapq
import matplotlib.pyplot as plt
class BidirectionalAStar:
def __init__(self, s_start, s_goal, heuristic_type,xI, xG):
self.s_start = s_start
self.s_goal = s_goal
self.heuristic_type = heuristic_type
self.motions = [(-1, 0), (-1, 1), (0, 1), (1, 1),
(1, 0), (1, -1), (0, -1), (-1, -1)]
self.u_set = self.motions # feasible input set
self.obs = self.obs_map() # position of obstacles
self.OPEN_fore = [] # OPEN set for forward searching
self.OPEN_back = [] # OPEN set for backward searching
self.CLOSED_fore = [] # CLOSED set for forward
self.CLOSED_back = [] # CLOSED set for backward
self.PARENT_fore = dict() # recorded parent for forward
self.PARENT_back = dict() # recorded parent for backward
self.g_fore = dict() # cost to come for forward
self.g_back = dict() # cost to come for backward
self.x_range = 51 # size of background
self.y_range = 31
self.xI, self.xG = xI, xG
self.obs = self.obs_map()
def init(self):
"""
initialize parameters
"""
self.g_fore[self.s_start] = 0.0
self.g_fore[self.s_goal] = math.inf
self.g_back[self.s_goal] = 0.0
self.g_back[self.s_start] = math.inf
self.PARENT_fore[self.s_start] = self.s_start
self.PARENT_back[self.s_goal] = self.s_goal
heapq.heappush(self.OPEN_fore,
(self.f_value_fore(self.s_start), self.s_start))
heapq.heappush(self.OPEN_back,
(self.f_value_back(self.s_goal), self.s_goal))
def obs_map(self):
"""
Initialize obstacles' positions
:return: map of obstacles
"""
x = 51
y = 31
obs = set()
for i in range(x):
obs.add((i, 0))
for i in range(x):
obs.add((i, y - 1))
for i in range(y):
obs.add((0, i))
for i in range(y):
obs.add((x - 1, i))
for i in range(10, 21):
obs.add((i, 15))
for i in range(15):
obs.add((20, i))
for i in range(15, 30):
obs.add((30, i))
for i in range(16):
obs.add((40, i))
return obs
def animation_bi_astar(self, path, v_fore, v_back, name):
self.plot_grid(name)
self.plot_visited_bi(v_fore, v_back)
self.plot_path(path)
plt.show()
def plot_grid(self, name):
obs_x = [x[0] for x in self.obs]
obs_y = [x[1] for x in self.obs]
plt.plot(self.xI[0], self.xI[1], "bs")
plt.plot(self.xG[0], self.xG[1], "gs")
plt.plot(obs_x, obs_y, "sk")
plt.title(name)
plt.axis("equal")
def plot_visited(self, visited, cl='gray'):
if self.xI in visited:
visited.remove(self.xI)
if self.xG in visited:
visited.remove(self.xG)
count = 0
for x in visited:
count += 1
plt.plot(x[0], x[1], color=cl, marker='o')
plt.gcf().canvas.mpl_connect('key_release_event',
lambda event: [exit(0) if event.key == 'escape' else None])
if count < len(visited) / 3:
length = 20
elif count < len(visited) * 2 / 3:
length = 30
else:
length = 40
#
# length = 15
if count % length == 0:
plt.pause(0.001)
plt.pause(0.01)
def plot_path(self, path, cl='r', flag=False):
path_x = [path[i][0] for i in range(len(path))]
path_y = [path[i][1] for i in range(len(path))]
if not flag:
plt.plot(path_x, path_y, linewidth='3', color='r')
else:
plt.plot(path_x, path_y, linewidth='3', color=cl)
plt.plot(self.xI[0], self.xI[1], "bs")
plt.plot(self.xG[0], self.xG[1], "gs")
plt.pause(0.01)
def plot_visited_bi(self, v_fore, v_back):
if self.xI in v_fore:
v_fore.remove(self.xI)
if self.xG in v_back:
v_back.remove(self.xG)
len_fore, len_back = len(v_fore), len(v_back)
for k in range(max(len_fore, len_back)):
if k < len_fore:
plt.plot(v_fore[k][0], v_fore[k][1], linewidth='3', color='gray', marker='o')
if k < len_back:
plt.plot(v_back[k][0], v_back[k][1], linewidth='3', color='cornflowerblue', marker='o')
plt.gcf().canvas.mpl_connect('key_release_event',
lambda event: [exit(0) if event.key == 'escape' else None])
if k % 10 == 0:
plt.pause(0.001)
plt.pause(0.01)
def searching(self):
"""
Bidirectional A*
:return: connected path, visited order of forward, visited order of backward
"""
self.init()
s_meet = self.s_start
while self.OPEN_fore and self.OPEN_back:
# solve foreward-search
_, s_fore = heapq.heappop(self.OPEN_fore)
if s_fore in self.PARENT_back:
s_meet = s_fore
break
#前向路径走过的点,用于可视化
self.CLOSED_fore.append(s_fore)
for s_n in self.get_neighbor(s_fore):
new_cost = self.g_fore[s_fore] + self.cost(s_fore, s_n)
if s_n not in self.g_fore:
self.g_fore[s_n] = math.inf
if new_cost < self.g_fore[s_n]:
self.g_fore[s_n] = new_cost
self.PARENT_fore[s_n] = s_fore
heapq.heappush(self.OPEN_fore,
(self.f_value_fore(s_n), s_n))
# solve backward-search
_, s_back = heapq.heappop(self.OPEN_back)
if s_back in self.PARENT_fore:
s_meet = s_back
break
self.CLOSED_back.append(s_back)
for s_n in self.get_neighbor(s_back):
new_cost = self.g_back[s_back] + self.cost(s_back, s_n)
if s_n not in self.g_back:
self.g_back[s_n] = math.inf
if new_cost < self.g_back[s_n]:
self.g_back[s_n] = new_cost
self.PARENT_back[s_n] = s_back
heapq.heappush(self.OPEN_back,
(self.f_value_back(s_n), s_n))
return self.extract_path(s_meet), self.CLOSED_fore, self.CLOSED_back
def get_neighbor(self, s):
"""
find neighbors of state s that not in obstacles.
:param s: state
:return: neighbors
"""
return [(s[0] + u[0], s[1] + u[1]) for u in self.u_set]
def extract_path(self, s_meet):
"""
extract path from start and goal
:param s_meet: meet point of bi-direction a*
:return: path
"""
# extract path for foreward part
path_fore = [s_meet]
s = s_meet
while True:
s = self.PARENT_fore[s]
path_fore.append(s)
if s == self.s_start:
break
# extract path for backward part
path_back = []
s = s_meet
while True:
s = self.PARENT_back[s]
path_back.append(s)
if s == self.s_goal:
break
return list(reversed(path_fore)) + list(path_back)
def f_value_fore(self, s):
"""
forward searching: f = g + h. (g: Cost to come, h: heuristic value)
:param s: current state
:return: f
"""
return self.g_fore[s] + self.h(s, self.s_goal)
def f_value_back(self, s):
"""
backward searching: f = g + h. (g: Cost to come, h: heuristic value)
:param s: current state
:return: f
"""
return self.g_back[s] + self.h(s, self.s_start)
def h(self, s, goal):
"""
Calculate heuristic value.
:param s: current node (state)
:param goal: goal node (state)
:return: heuristic value
"""
heuristic_type = self.heuristic_type
if heuristic_type == "manhattan":
return abs(goal[0] - s[0]) + abs(goal[1] - s[1])
else:
return math.hypot(goal[0] - s[0], goal[1] - s[1])
def cost(self, s_start, s_goal):
"""
Calculate Cost for this motion
:param s_start: starting node
:param s_goal: end node
:return: Cost for this motion
:note: Cost function could be more complicate!
"""
if self.is_collision(s_start, s_goal):
return math.inf
return math.hypot(s_goal[0] - s_start[0], s_goal[1] - s_start[1])
def is_collision(self, s_start, s_end):
"""
check if the line segment (s_start, s_end) is collision.
:param s_start: start node
:param s_end: end node
:return: True: is collision / False: not collision
"""
if s_start in self.obs or s_end in self.obs:
return True
if s_start[0] != s_end[0] and s_start[1] != s_end[1]:
if s_end[0] - s_start[0] == s_start[1] - s_end[1]:
s1 = (min(s_start[0], s_end[0]), min(s_start[1], s_end[1]))
s2 = (max(s_start[0], s_end[0]), max(s_start[1], s_end[1]))
else:
s1 = (min(s_start[0], s_end[0]), max(s_start[1], s_end[1]))
s2 = (max(s_start[0], s_end[0]), min(s_start[1], s_end[1]))
if s1 in self.obs or s2 in self.obs:
return True
return False
def main():
x_start = (5, 5)
x_goal = (45, 25)
bastar = BidirectionalAStar(x_start, x_goal, "euclidean",x_start,x_goal)
path, visited_fore, visited_back = bastar.searching()
bastar.animation_bi_astar(path, visited_fore, visited_back, "Bidirectional-A*") # animation
if __name__ == '__main__':
main()
代码讲解
首先在程序开始时先初始了两个字典
self.PARENT_fore[self.s_start] = self.s_start
self.PARENT_back[self.s_goal] = self.s_goal
然后再初始化了两个堆栈:
heapq.heappush(self.OPEN_fore,
(self.f_value_fore(self.s_start), self.s_start))
heapq.heappush(self.OPEN_back,
(self.f_value_back(self.s_goal), self.s_goal))
两个字典是用于存放走过的路径,前者存放从起点往终点搜索的路径,后者存放从终点往起点搜索过的路径。字典的作用是用于回朔路径,即该点是从哪个点索引过来的。比如说从起点搜索经过点1,点1搜索四周时到达点4,点4搜索时又到达点8,则可以根据回朔找到回去的路径8->4->1。
两个堆栈的作用是用于对每个点的代价值进行排序,因为A* 本身搜索的时候是根据每个点的代价值作为条件的,优先搜索代价值最小的点。所以使用两个堆栈进行点的排序。堆栈可以对每个点的值按照从大到小向上排序,所以需要取代价值最小的点只需要栈顶出栈就可以了。
接下来对起点与终点周围的点进行遍历,计算每个点的代价值并存放到两个堆栈中,并将经过的点排入到字典中。
for s_n in self.get_neighbor(s_fore):
new_cost = self.g_fore[s_fore] + self.cost(s_fore, s_n)
if s_n not in self.g_fore:
self.g_fore[s_n] = math.inf
if new_cost < self.g_fore[s_n]:
self.g_fore[s_n] = new_cost
self.PARENT_fore[s_n] = s_fore
heapq.heappush(self.OPEN_fore,
(self.f_value_fore(s_n), s_n))
for s_n in self.get_neighbor(s_back):
new_cost = self.g_back[s_back] + self.cost(s_back, s_n)
if s_n not in self.g_back:
self.g_back[s_n] = math.inf
if new_cost < self.g_back[s_n]:
self.g_back[s_n] = new_cost
self.PARENT_back[s_n] = s_back
heapq.heappush(self.OPEN_back,
(self.f_value_back(s_n), s_n))
这里注意前后两个点的代价值计算方式是不一样的,前者的计算为:
def f_value_fore(self, s):
return self.g_fore[s] + self.h(s, self.s_goal)
def h(self, s, goal):
heuristic_type = self.heuristic_type
if heuristic_type == "manhattan":
return abs(goal[0] - s[0]) + abs(goal[1] - s[1])
else:
return math.hypot(goal[0] - s[0], goal[1] - s[1])
后者的计算为:
def f_value_back(self, s):
return self.g_back[s] + self.h(s, self.s_start)
此时判断堆栈中是否为空,如果不为空的话就循环出栈对周围进行搜索,直到起点的搜索点位出现再终点所搜索过的字典中或者终点的搜索点位出现在起点所搜索过的字典中,则说明两边的点位相接触了,已经找到了最终的路径:
if s_fore in self.PARENT_back:
s_meet = s_fore
break
if s_back in self.PARENT_fore:
s_meet = s_back
break
然后再根据两个字典向两边搜索得到最终的路径即可:
def extract_path(self, s_meet):
# extract path for foreward part
path_fore = [s_meet]
s = s_meet
while True:
s = self.PARENT_fore[s]
path_fore.append(s)
if s == self.s_start:
break
# extract path for backward part
path_back = []
s = s_meet
while True:
s = self.PARENT_back[s]
path_back.append(s)
if s == self.s_goal:
break
return list(reversed(path_fore)) + list(path_back)
结果
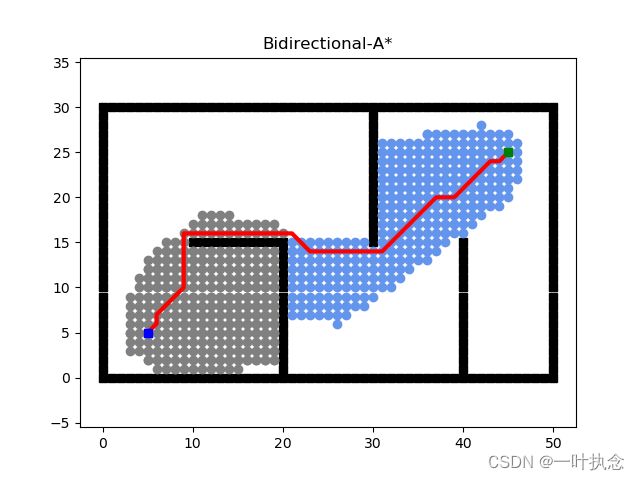
需要注意的是:双向A* 算法的优势在于它可以从起点和终点同时进行搜索,通过双向信息的利用减少搜索的节点数量,提高搜索效率。然而,它也需要更多的空间来存储两个方向的搜索路径和节点信息。因为单向A* 只需要一个字典一个堆栈就可以完成遍历,但是双向A* 需要维护两个字典与堆栈。