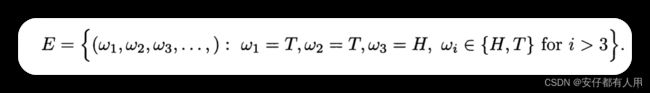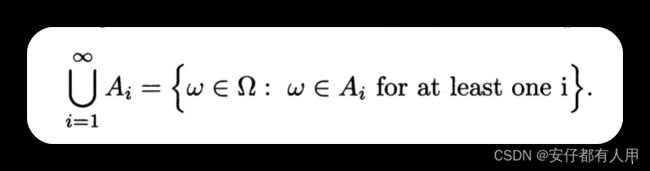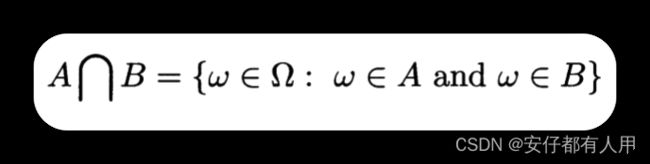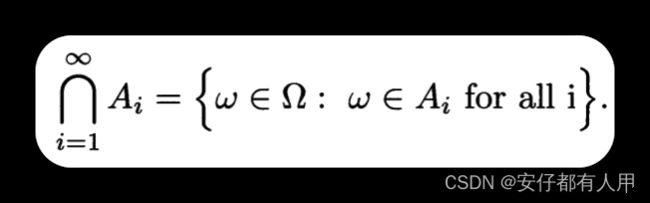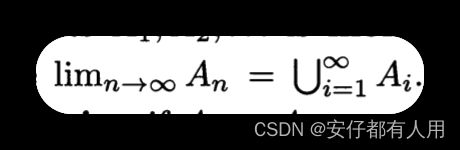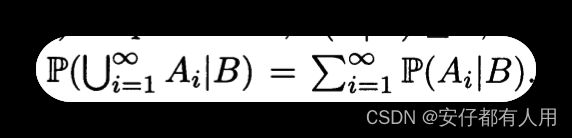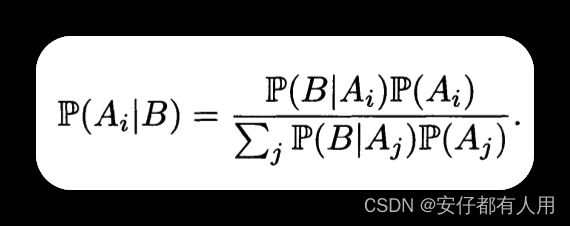All of Statistics 第一章

统计学（一）概率(Probability)

为了学习机器学习，现在重新学习一下统计学，然后将整个学习过程记录下来。本篇为学习笔记，主要翻译自《all of statistics》by Larry Wasserman

本章内容
1.1 引言
1.2 样本空间和事件(sample space and events)
1.3 概率(Probability)
1.4 有限采样空间中的概率
1.5 独立事件
1.6 条件概率
1.7 贝叶斯定理

因为将英文名词翻译成中文名词时,往往有些言不达意,因此将一些名词的中英文都给出,其实对于名词的理解直接使用英文名词,理解会更加深刻一点

关键名词:

1. 样本空间:sample space
2. 事件:events
3. 样本结果:sample outcoms
4. 实际结果:realizations
5. 样本元素或元素:elements
6. 不相交:disjoint
7. 互斥:mutually exclusive
8. 示性函数,或者指示函数:indicator function
9. 概率分布:probability distribution
10. 概率测度:probability measure
11. 公理:Axiom
12. 频率:frequency
13. 可信度:degree of belief
14. 频率主义学派:frequentist
15. 贝叶斯学派:Bayesian schools
16. 引理:lemma
17. 定理:Theorem
18. 等可能性:equally likely
19. 均匀概率分布:uniform probability distribution.
20. 组合方法:combinatorial methods
21. 独立事件:Independent Events
22. 韦恩图:Venn diagram
23. 条件概率:Conditional Probability
24. 专家系统:expert system
25. 贝叶斯网络:Bayes’ nets
26. 全概率定理或者总概率定理:The Law of Total Probability
27. 先验概率:prior probability
28. 后验概率:posterior probability

1.1 引言

概率(Probability)是一种量化不确定的数学语言。在本章，我们将介绍概率论下的基本概念。首先我们从样本空间(sample space)开始，样本空间是所有可能结果的集合。

1.2 样本空间和事件

样本空间(sample space) Ω 表示一个随机试验中所有可能结果的集合。而小写的ω表示样本空间中的一点，称为样本结果(sample outcomes),或者称为实际结果(realizations),或者称为样本元素(elements).

样本空间Ω中的子集称为事件(Events)

1.1 例子

如果我们抛硬币两次，那么 Ω={HH,HT,TH,TT},第一次抛硬币出现正面的事件A={HH,HT}

1.2 例子

令 ω 是对某个物理量进行测量的结果，如温度。那么Ω=R={-∞，∞},有人可能会说将Ω定义为R并不精确，因为温度有最低限度。但，样本空间比实际大的时候，通常并不会有问题。

那么温度大于10，小于等于23的事件A可以表示为A=(10,23]

1.3 例子

注意,因为文本有些难以描述复杂的数学式子,因此一些复杂的数学式子,将会使用图片代替

如果我们无限的抛硬币，那么样本空间将会是无限集合。可以表示为：

Ω= {ω=(ω1,ω2,ω3,…,):ω∈{H,T}}

令E是第一次出现正面在第三抛硬币的时候,那么E可以表示为:

E={(ω1,ω2,ω3,…,): ω1=T,ω2=T,ω3=H,ωi∈{H,T} 对于 i>3}

补集,并集,交集,差的符号写法

给定一个事件A,用下面的式子表示A的补集

从形式上看,A^c,可以读作"not A".

那么Ω的补集就为∅.

事件A和事件B的并集就为:

上面的式子,可以被认为:A或者B.

如果A1,A2…是集合序列,那么他们的并集可以表示为:

事件A和事件B的交集就为:

读作:A and B,有时将交集写成AB或者(A,B)

如果A1,A2,…是集合序列,那么他们的交集可以表示为:

集合之间的差,则为如下的定义:

如果A中的每一个元素(elements)也蕴含在B中,那么可以写为

等价的写法,还有

如果A是有限集合,那 |A|表示A中元素个数

下图给出一个总览

互斥,不相交

如果Ai∩Aj=∅,i ≠ j,那么我们就说A1,A2,…不相交(disjoint),或者互斥(mutually exclusive)

例如,A1=(0,1],A2=(1,2],A3=(2,3],…是不相交的.

将Ω划分成一些列不相交的集合,A1,A2,A3,…那么他们满足

示性函数或者指示函数(indicator function)

A的示性函数,或者指示函数,被定义为:

单调递增和单调递减

如果A1 ⊂ A2 ⊂ A3 ⊂ A4 … ,并且我们按照如下定义An

那么我们就成A1,A2,A3,…是单调递增的

如果A1 ⊃ A2 ⊃ A3 ⊃ A4…,并且我们按照如下定义An

1.4 例子

因为无法文本不好打字,直接提供图片

1.3 概率(Probability)

我们将为事件A分配一个实数P(A),称之为A的概率.我们称这个P为概率分布(probability distribution)或者概率测度(probability measure)

1.5 概率分布(Probability distribution )或者概率测度(Probability measure)的定义

如果函数P,对于每个事件A,都有P(A)为一个实数,且满足下面的三个公理(axiom),那么P就是概率分布(Probability distribution)或者概率测度(Probability measure)

1. 公理1(axiom 1) : P(A) ≥ 0
2. 公理2(axiom 2) : P(Ω) = 1
3. 公理3(axiom 3):如果A1,A2,…不相交,那么交集的概率分布等于各个子集概率分布之和.式子如下图
   

P(A)存在很多解释和理解,有两种最常见的解释:频率(frequencies)和可信度(degree of belief).用频率来解释就是,在重复试验中,P(A)表示事件A为真的次数在长时间运行次数中所占的比例.

例如,当我们说硬币正面朝上的概率为1/2,那么就意味着,在多次抛掷硬币的试验中,随着抛掷的次数增加,正面朝上的次数占总次数的比例趋向于1/2

在一个无限长,不可预测的抛掷序列中,正面朝上的比例极限趋向于一个常数,这是一种理想情况,这种理想情况,就向几何学中的直线一样.

用可信度(degree-of-belief)来解释就是,P(A)衡量了观测者相信A为真的强度.

无论是哪一种解释,我们都要求他们满足上面三个公理.而这两种解释的差异,在处理统计推断之前都不会有太大关系.在统计推断中,这两种不同的解释,导致了两种不同的推断学派:频率主义学派(frequentist)和贝叶斯学派(Bayesian schools).我们将在第十一章中进行讨论

我们可以从上面的三个公理推出P的许多性质,如下

在下面的引理(Lemma)中,给出了一个不太明显的性质

1.6 引理(lemma)

对于任意事件A和B,他们满足如下的式子

P(A∪B) = P(A) + P(B) - P(AB)

证明:因为补集不好打印,所以我直接添加手动证明的图片

1.7 例子

抛掷两枚硬币,令H1是第一次正面朝上的事件,H2是第二次正面朝上的事件,如果所有结果可能性相等(equally likely),那么P(H1∪H2) = P(H1) + P(H2) - P(H1H1) = 1/2 + 1/2 -1/4 = 3/4

1.8 概率连续性定理(Theorem)

当 n ⟶ ∞ 时,如果 An ⟶ A,那么 P(An) ⟶ P(A)

证明如下:

1.4 有限样本空间的概率(Probability on Finite Sample Spaces)

假定样本空间是有限的 Ω = {ω1,ω2,ω3,…}.如,我们投掷两次骰子,那么样本空间Ω将会有36个元素Ω = {(i,j);i,j∈{1,…6}}.如果每个结果可能性相等(equally likely).那么P(A)= |A|/36.其中|A|表示事件A中元素的个数

骰子点数总和为11的概率为2/36,因为只有两种结果对应这个事件.

如果Ω是有限的,且每一个结果都是等可能的(equally likely),那么

P(A)=|A|/|Ω|

这被称为:**均匀概率分布(uniform probability distribution) **.

为了计算概率,就需要计算事件A的点(point)数.计算点数(points)的方法被称为组合方法(combinatorial methods).我们不需要深入组合方法(combinatorial methods)的细节,但我们需要一些计算理论的知识,方便以后使用.

给定n个对象,排列这些对象的,排列个数有:n!=n(n-1)(n-2)(n-3)...1,其中0!=1.

我们还可以按照如下来定义,

读作:n个选择k个,它表示了从n个对象中,选择k个对象,有多少种选择.

例如,我们有一个班级20人,需要选择3个当班委,那么就有这么多种选择

我们还可能观测到如下的性质

1.5 独立事件(Independent Events)

如果我们抛一枚硬币两次,那么两次都是正面的概率为1/2*1/2=1/4.我们直接将概率相乘,是因为我们认为这两个事件是独立的.

独立事件的正规定义如下:

1.9 独立事件的定义

如果P(AB) = P(A) * P(B) ,那么A和B是独立的(independent),写作A∐B

如果满足下面的式子,则称事件集(a set of events)是独立的

如果A和B不独立,写作如下格式

独立性可以以两种不同的方式产生.第一种,明确假定两个事件是独立的.例如,在两次抛掷硬币的过程中,我们假定抛掷是独立的,这种独立性反应了硬币不会记住第一次的抛掷.

第二种,通过验证P(AB)=P(A)P(B)的成立,推断出A和B是相互独立的.例如,在投掷一个均匀的骰子时,令A={2,4,6},B={1,2,3,4}.那么A∩B={2,4}.P(AB)=2/6=P(A)P(B)=(1/2)(2/3).因此我们可以得出A和B是独立的. 在这个例子中, 我们并没有假定A和B是独立的,事实上他们确实是独立的.

假定,A和B不相交,且每个事件的概率为正,那么他们是独立的吗?

答案是,不独立.因为P(A)P(B)>0,但是P(AB)=P(∅)=0

因此通过这个例子,就可以得出,通过韦恩图(Venn diagram)是不能判断事件是否独立的.

1.10 例子

抛掷硬币10次,令A=至少一个正面,令Tj=第j次出现反面,那么P(A)为多少

P(A) = 1- P(A的补集)=1-P(所有都是反面)=1-P(T1T2..T10)
    = 1-P(T1)*P(T2)...P(T10)
    = 1- (1/2) * (1/2) ... * (1/2)
    ≈ 0.999

1.11 例子

两人轮流投篮,第一个人成功的概率为1/3,第二个人成功的概率为1/4,第一个人比第二个人先成功投进的概率是多少

下面给出独立性的总结

1.6 条件概率(Conditional Probability)

假如P(B)>0,我们定义,在B发生的条件下A发生的概率为:

1.12 条件概率(conditional probability)定义

如果P(B)>0,那么,B发生的条件下,A的条件概率(conditional probability)为:

P(A|B) = P(AB)/P(B)

将条件概率视为,B发生的情况中,A发生的比例.

对于任何一个固定的B来讲,P(B)>0,那么P(·|B)就是概率(即满足前文中的三个公理).特别是,P(A|B)>0,P(Ω|B)=1,若A1,A2,…不相交,那么

但,P(A|B∪C) = P(A|B) + P(A|C)通常并不成立,概率的运算规则通常运用在竖线的左侧,而不是竖线的右侧.

P(A|B) = P(B|A)通常也不成立.人们经常对这条规则感到困惑.例如,假如你患有麻疹,那么你有红斑的概率为1,但是,你有红斑的条件下,你患麻疹的概率并不为1.

在这种情况下,P(A|B)和P(B|A)的差异显而易见,但依然有一些情况,让这种差异非常难以察觉.这在法律案件中,常常发生,有时被称为:prosecutor’s fallacy(检察官的谬误)

1.13 例子

对于疾病D来说,药物测试的结果为+或-,他们的概率为

x	D	D的补集
+	.009	.099
-	.001	.891

根据条件概率的定义,得

P(+|D)=P(+∩D)/P(D)=.009/(.009+.001)=.9

P(-|D的补集)=P(-∩(D的补集))/P(D的补集)=.891/(.891+.099)≈.9

显然,它的测试非常的精确,有病的情况下为阳性(+)的概率为.9,没有病的情况下,为阴性(-)的概率约为0.9

假定,你做了这个测试,并且是阳性(+),那么你患病的概率是多少呢?大多数的答案可能是90%,但正确的答案是:

P(D|+)=P(D∩+)/P(+)=.009/(.009+.099)≈.08

这里的教训是,你需要通过数值计算来得出答案,而不要通过直觉

下面的引理(lemma)直接来源于条件概率(conditional probability)的定义

1.14 引理

如果A和B是独立事件,那么P(A|B)=P(A),当然,对于任何的A,B事件对,则满足

P(AB)= P(A|B)P(B) = P(B|A)P(A)

从上面这个引理,我们可以看到独立事件的另外一个解释,即,B的发生并不会改变A的概率.式子P(AB)=P(A)P(B|A)在计算某些概率时特别有用

1.15 例子

从一副牌中,不放回,抽出两张,假设A是第一次抽到梅花A的事件,B是第二次抽到方块Q的事件, 那么P(AB)=P§P(B|A)=(1/52)*(1/51)

下面给出条件概率的总结

1.7 贝叶斯定理(Bayes’ Theorem)

贝叶斯理论是专家系统(expert system)和贝叶斯网络(Bayes’ nets)的基础,贝叶斯网络在第十七章介绍,首先我们需要一点预备理论结果

1.16 全概率定理或者总概率定理(The Law of Total Probability)

设Ω为A1,A2,…Ak,对于任何一个事件B来说,P(B)等于

证明,如下

1.17 贝叶斯定理(Bayes’ Theorem)

设Ω为A1,A2,…Ak,满足P(Ai)>0,如果P(B)>0,那么对于i = 1,…,k 则有

1.18 说明

我们称P(Ai)为A的先验概率(prior probability),P(Ai|B)为A的后验概率(posterior probability)

证明:我们运用两次条件概率的定义即可,如下

1.19 例子

我将email分成三类,A1=“垃圾邮件(Spam)”,A2=“低优先级邮件(low priority)”,A3=“高优先级邮件(hight priority)”.根据经验,我得到了他们的概率,P(A1)=.7,P(A2)=.2,P(A3)=.1

当然.7+.2+.1=1.设事件B是邮件中包含单词"free".根据经验可得P(B|A1)=.9,P(B|A2)=.01,P(B|A3)=.01

注意:.9+.01+.01≠1

现在我收到一封邮件,带有"free"单词,那么它为垃圾邮件的概率为多少?

根据贝叶斯定理得:

P(A1|B)=(.9*.7)/{(.9*.7)+(.01*.2)+(.01*.1)}=.995

第一章完,

未翻译,文献注释,附录和课后作业