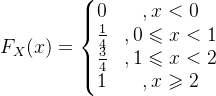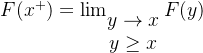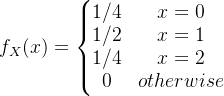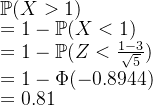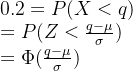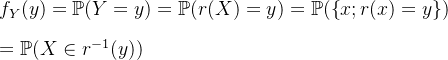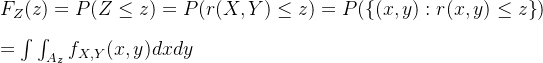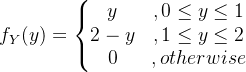All of Statistics 第二章
统计学(二)随机变量(Random Variables)
本章内容
- 引言
- 分布函数和概率分布(Distribution Functions and Probability Functions)
- 一些重要的离散随机变量(Discrete Random Variables )
- 一些重要的连续随机变量(Continuous Random Variables)
- 二维分布(Bivariate Distributions )
- 边缘分布(Marginal Distributions )
- 独立随机变量
- 条件分布(Conditional Distributions )
- 多维分布(Multivariate Distributions)和独立同步分布(IID)
- 两个重要的多维分布
- 随机变量的转换
- 多个随机变量的转换
关键名词,存在部分词不达意的情况,因此将关键名词整理如下
1. 分布函数:Distribution Functions
2. 概率函数:Probability Functions
3. 离散随机变量:Discrete Random Variables
4. 连续随机变量:Continuous Random Variables
5. 二维分布:Bivariate Distributions
6. 边缘分布:Marginal Distributions
7. 条件分布:Conditional Distributions
8. 多维分布:Multivariate Distributions9. 累积分布函数:cumulative distribution function
10. 标准化:normalized
11. 概率函数:Probability function
12. 概率质量函数:Probability mass function
13. 概率密度函数:Probability density funciton
14. 连续:continuous
15. 分位函数:quantile function
16. 第一四分位:first quartile
17. 第二四分位:second quartile
18. 第三四分位:third quartile
19. 中位数:median
20. 等概率分布:equal in distribution
21. 点质量分布: Point Mass Distribution
22. 离散均匀分布:Discrete Uniform Distribution
23. 伯努利分布:Bernuolli Distribution
24. 二项分布:Binomial Distribution
25. 几何分布:Geometric Distribution
26. 泊松分布:Possion Distribution
27. 正态分布:Normal Distribution
28. 高斯分布:Gaussian Distribution
29. 标准正态分布:Standard Normal Distribution
30. 指数分布:Exponential Distribution
31. 伽马分布:Gamma Distribution
32. 贝塔分布:Beta Distribution
33. 柯西分布:Cauchy Distribution
34. 边缘分布:Marginal Distributions
35. 边缘质量函数:marginal mass function
36. 边缘密度函数:marginal denstiy function
37. 条件概率质量函数:Conditional Probability mass function
38. 条件概率密度函数:Conditional Probability Density funciton
40. 随机向量:Random Vector
41. 多项分布:Multinomial Distribution
42. 多元正态分布或者多维正态分布:Multivariate Normal
2.1 引言
统计学和数据挖掘关心的是数据,那么我们怎样将样本空间(sample)和事件(events)同数据联系起来呢?这种联系由随机变量(random variables)提供
2.1 随机变量(random variables)的定义
随机变量是一种映射,表示为 ![]() ,即对于每一个结果ω,都有一个实数被分配给X(ω).
,即对于每一个结果ω,都有一个实数被分配给X(ω).
在概率课程的某些阶段,我们很少再提及样本空间(sapmle space),而是直接使用随机变量(random variables).但你应该牢记,样本空间(sample space)实际是存在,它隐含在随机变量的背后.
2.2 例子
抛硬币十次,令X(ω)是序列ω中正面朝上的个数,例如,ω=HHTHHTHHTT,那么X(ω)=6.
2.3 例子
设![]() 是一个单位圆,在Ω中随机取一点(我们将在后面更精确的描述这个想法),通常格式为ω=(x,y).那么随机变量的一些例子有:X(ω) = x,Y(ω) = y,Z(ω) = x+y或者
是一个单位圆,在Ω中随机取一点(我们将在后面更精确的描述这个想法),通常格式为ω=(x,y).那么随机变量的一些例子有:X(ω) = x,Y(ω) = y,Z(ω) = x+y或者![]()
给定一个随机变量X和实数的子集A,定义![]() 并令
并令
![]()
![]()
注意:X是随机变量,x是随机变量X的具体值
2.4 例子
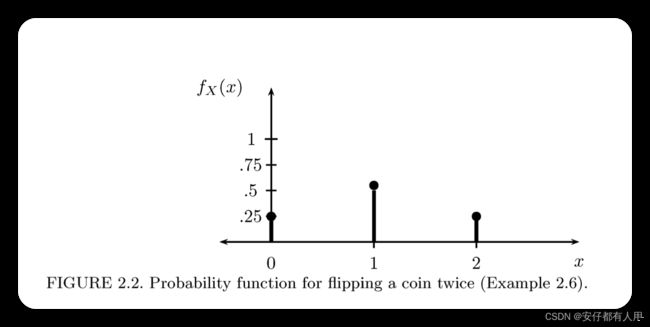
抛硬币两次,令X为正面朝上的个数,那么P(X=0)=P({TT})=1/4, P(X=1)=P({HT,TH})=1/2 , P(X=2)=P({HH})=1/4,随机变量(random variables)和它的分布(distribution)可以总结如下:
| ω | P({ω}) | X(ω) |
| TT | 1/4 |
0 |
| TH | 1/4 | 1 |
| HT | 1/4 | 1 |
| HH | 1/4 | 2 |
| x | P(X=x) |
| 0 | 1/4 |
| 1 | 1/2 |
| 2 | 1/2 |
2.2 分布函数(distribution functions)和概率函数(Probability functions)
给定一个随机变量X,我们按照如下的方式,定义其累积分布函数(cumulative distribution function)或分布函数(distribution functions):
2.5 CDF定义
累积分布函数(cumulative distribution function)或者CDF,![]() 被定义为
被定义为
![]()
在后面,我们将会看到CDF有效地包含了所有关于随机变量的信息.有时我们用![]() 代替
代替![]() .
.
2.6 例子
扔一枚硬币两次,设X是正面朝上的次数.那么![]() ,则分布函数为:
,则分布函数为:
则其对应的函数图形如下图
尽管这个例子非常简单,但是也请仔细的研究它,因为CDF的性质可能令人困惑.
注意,这个函数,是右连续,非递减,尽管x只取0,1,2但对所有的实数都有定义.你明白了为什么![]() 了吗?
了吗?
以下的定理表明,CDF完全决定了随机变量(random variables)的分布
2.7 定理
设X有累积分布函数(CDF)F,Y有累积分布函数(CDF)G,如果对于所有的x,满足![]() ,那么对于所有的A,则有
,那么对于所有的A,则有![]()
译者注:上面的定理可以看成CDF决定了概率分布
2.8 定理
F是[0,1]上的映射,当且仅当F满足下面三个条件的时候, F是某个概率P的累积分布函数.
证明:
假定F是CDF,让我们证明第三点成立.
设x是一个实数;
y1,y1,...是一个实数序列,满足y1>y2>...并且![]() .
.
那么,![]()
则得,![]() ,
,![]()
所以,![]()
所以,![]()
证毕
第一点和第二点类似.
证明另外一个方向------即,倘若F满足第一二三点,证明F是某个概率P的CDF-----需要使用分析领域更深层次的工具.
2.9 概率函数(Probability function)或概率质量函数(Probability mass function)定义
如果随机变量X取值有限,且离散.那么X的概率函数(probability function)或者概率质量函数(probability mass function)被定义为:
![]() .
.
因此,对于所有的![]() ,都有
,都有![]() ,且
,且![]() .有时我们直接用
.有时我们直接用![]() 代替
代替![]() .
.
CDF和![]() 的关系为:
的关系为:
![]()
2.10 例子
2.6例子的概率函数(probability function)为
见下图
2.11 概率密度函数(probability density function)定义
对于一个连续(continuous)的随机变量X,如果对于所有的x,存在一个函数![]() 满足
满足![]() ,
,![]() ,且满足,
,且满足,![]() ,那么就称
,那么就称![]() 为概率密度函数(probability density function)PDF.
为概率密度函数(probability density function)PDF.
因此可以得![]() 和
和![]() ,其中在所有x点处,
,其中在所有x点处,![]() 都是可导的.
都是可导的.
有时,我们用![]() 或者
或者![]() 来表示
来表示![]()
2.12 例子
设随机变量X的概率密度函数PDF,如下
显然,![]() 且
且 ![]() .那么带有这种PDF的随机变量被称为 Uniform(0,1) 分布.Uniform(0,1)分布的概念表示,在[0,1]区间中随机选择一个点.
.那么带有这种PDF的随机变量被称为 Uniform(0,1) 分布.Uniform(0,1)分布的概念表示,在[0,1]区间中随机选择一个点.
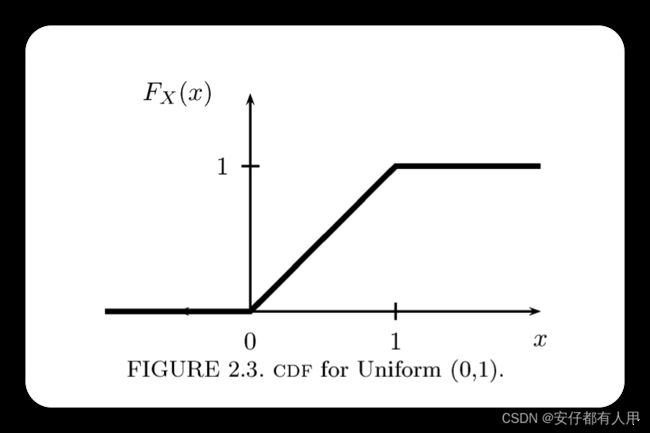
那么CDF,就为:
![]()
如下图:
2.13 例子
假如随机变量X,有下面的PDF:
因为![]() ,这是一个满足定义的PDF
,这是一个满足定义的PDF
警告;连续随机变量可能带来困惑.
首先应注意,如果X是连续的,那么对于任意x,都有![]() 不要尝试将
不要尝试将![]() 当做
当做![]() ,这个只对离散随机变量有效. 连续随机变量对应的概率是通过PDF的积分得到.
,这个只对离散随机变量有效. 连续随机变量对应的概率是通过PDF的积分得到.
其次还要注意,PDF是可以大于1的(这个跟概率质量函数(probability mass function)不同),例如:
![]() 可得,
可得,![]() 且
且![]() ,因此其是一个满足定义的PDF,但其在某些区间可得f(x)=5.事实上,PDF,可以是无界的,例如:
,因此其是一个满足定义的PDF,但其在某些区间可得f(x)=5.事实上,PDF,可以是无界的,例如: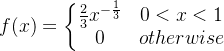 ,可得
,可得![]() ,因此也是一个符合定义的PDF,但是它是无解函数.
,因此也是一个符合定义的PDF,但是它是无解函数.
2.14 例子
![]()
2.15 引理
设F是随机变量X的CDF,那么:
这对于定义CDF的逆函数(或者分位函数(quantile function))是有用的.
2.16 CDF的逆函数或者分位函数的定义
设X是一个有累积分布函数F的随机变量.那么CDF的逆函数或者分位函数(quantile function)被定义为:
![]() ,其中
,其中![]() ,
,
如果F是严格递增且连续,那么![]() 有唯一的实数x,使得
有唯一的实数x,使得![]()
我们将![]() 称为:第一四分位(first quartile) ;将
称为:第一四分位(first quartile) ;将![]() 称为:中位数(median)或者第二四分位(second quartile);将
称为:中位数(median)或者第二四分位(second quartile);将![]() 称为:第三四分位(third quartile)
称为:第三四分位(third quartile)
两个随机变量X和Y,它们是等概率分布(equal in distribution),则可以写成![]() .如果对于所有的x,都有
.如果对于所有的x,都有![]() ,这并不意味着X和Y是相等的.它只意味着X和Y有相同的概率状态.例如,设
,这并不意味着X和Y是相等的.它只意味着X和Y有相同的概率状态.例如,设![]() ,令Y=-X,则得
,令Y=-X,则得![]() ,所以
,所以![]() ,但X和Y是不相等的.事实上
,但X和Y是不相等的.事实上![]()
2.3 一些重要的离散随机变量
关于符号的警告:![]() 表示随机变量X的概率分布函数为F,这中传统的写法,并不合适,因为这个~符号也用来表示近似.符号
表示随机变量X的概率分布函数为F,这中传统的写法,并不合适,因为这个~符号也用来表示近似.符号![]() 太根深蒂固,以至于我们不得不沿用它.当我们看到这个符号的时候,应该将它当做:随机变量X满足分布F,而不是当做,X近似于F
太根深蒂固,以至于我们不得不沿用它.当我们看到这个符号的时候,应该将它当做:随机变量X满足分布F,而不是当做,X近似于F
Point Mass Distribution(点质量分布):如果概率满足下面的条件,那么随机变量X在a处有一个 Point Mass Distribution,写作![]() ,:
,:
![]() ,
,
那么![]() ,概率质量函数(probability mass function)则为
,概率质量函数(probability mass function)则为
Discrete Uniform Distribution(离散均匀分布):设k>1是一个整数,假定X有如下的概率质量函数(probability mass function):
那么我们就说X有一个在{1,...k}上的均匀分布
Bernuolli Distribution(伯努利分布):令X代表一次硬币的抛掷,那么P(X=1)=p,P(X=0)=1-p,其中p在[0,1]之间,我们就说X具有伯努利分布(Bernoulli Distributtion),写作![]() .则其概率函数
.则其概率函数![]()
Binomial Distribution(二项分布):假定硬币正面朝上的概率为p, ![]() .抛硬币n次,令X为正面朝上的次数,假设每次抛掷是独立的,令
.抛硬币n次,令X为正面朝上的次数,假设每次抛掷是独立的,令![]() 是其质量函数(mass function),则其展开如下:
是其质量函数(mass function),则其展开如下:
有这种质量函数的随机变量,我们称之为二项随机变量,写作![]() .如果
.如果![]() ,那么
,那么![]()
警告:让我们借此机会来防止一些易混淆点. X表示随机变量,x表示随机变量的具体取值;n和p是参数,即,固定的实数.参数p通常未知,必须从数据中得到,这也是统计推断的内容.在大多数统计模型中,同时存在随机变量和参数,不要将他们混淆了.
Geometirc Distribution(几何分布):如果X有如下的概率函数,则随机变量X服从参数为p的几何分布(geometric distribution),写作![]() :
:
![]()
我们可得:
![]()
将X视为抛硬币时,第一次出现正面所需的次数.
Possion Distribution(泊松分布):如果概率质量函数如下,则随机变量X服从参数为λ的泊松分布.写作:![]() :
:
![]()
注意:
![]()
泊松分布经常用来作为稀有事件的模型,如辐射衰减,交通事故.如果![]() 那么
那么![]()
警告:我们将随机变量定义为:一种从样本空间Ω到实数R上的一种映射,但在上面的分布中我们没有提及样本空间.正如我们早期提到过的,样本空间经常"消失",但它依然存在于背后.让我们来显式的构建一个伯努利随机变量,令Ω=[0,1],并定义P满足P([a,b])=b-a,其中 0 <= a <= b <= 1.取p为[0,1]上的定值,定义:
那么,P(X=1)=P(ω<=p)=P([0,p])=p且P(X=0)=1-p.因此X服从伯努利分布,写作![]() .我们不会为上面所有的分布都进行这样的操作.事实上,我们将随机变量视为随机数,但从形式上看,它是一种定义在样本空间中的映射.
.我们不会为上面所有的分布都进行这样的操作.事实上,我们将随机变量视为随机数,但从形式上看,它是一种定义在样本空间中的映射.
2.4 一些重要的连续随机变量
Uniform Distribution(均匀分布):如果X有如下的概率密度函数,则X满足均匀分布,写作![]() :
:
a Normal(Gaussian) Distribution(正态分布,或者高斯分布):如果概率密度函数满足如下,则X满足参数μ和σ的正态分布(Normal Distribution) 此处,μ 是实数R, σ > 0. 参数μ是分布的中心(或均值),σ是分布的离散程度(或标准差).(均值和标准差将会在下一章进行定义).正态分布在概率论和统计学中扮演了重要的角色.自然界中的许多现象也近似于正态分布.在后面我们会学习中心极限定理(Center Limit Theorem),该定理表明,随机变量之和的分布可以近似于正态分布. 如果μ=0,σ=1,则称之为标准正态分布(standard Normal distribution).传统规定,标准正太随机变量用Z表示,而其PDF和CDF用 下面给出一些有用的结论: 从1可以推到出: 因此,只要我们可以计算标准正态的CDF,就可以计算任何概率.所有的统计计算包,都能计算 假定 现在求 从标准表中, Exponential Distribution(指数分布):如果概率密度函数满足如下,则X满足参数为β的指数分布(Exponential Distribution),写作: 指数分布被用作建模电子元器件的生命周期,以及稀有事件之间的等待时间 Gamma Distribution(伽马分布):对于α>0,伽马函数(gamma function)定义为: 指数分布(Exponential Distribution)就是Gamma(1,β)分布.如果 Beta Distribution(贝塔分布):如果f(x)满足如下条件,则X满足参数为α>0,β>0的贝塔分布(beta distribution),写作: t and Cauchy Distribution(t和柯西分布):如果f(x)满足如下条件,则称X满足自由度为v的t分布,写作: t分布类似于正态分布,但其有更厚的尾部.事实上,正态分布对应于自由度v=∞的t分布 .而柯西分布则对应于v=1的t分布.概率密度函数为: 为了弄明白这确实是一个密度函数,对齐其积分得: 如果Z1,Z2,...Zp是独立的标准正态随机变量,那么有 给定一组离散的随机变量X和Y,定义联合质量函数(joint mass function)为: 此处有两个随机变量X和Y的二维分布,他们的取值为0或1 因此,f(1,1)=P(X=1,Y=1)=4/9 在连续情况下,如果满足下面三个条件,则称函数f(x,y)是变量(X,Y)的PDF 在离散和连续的情况下,我们定义联合CDF为 假设(X,Y)在单位正方形内是均匀的,那么有: 求P(X<1/2,Y<1/2). 事件A={X<1/2,Y<1/2}对应于单位正方形的一个子集.在这种情况下,对f在这个子集上求积分.求出A的面积为1/4.所以P(X<1/2,Y<1/2)=1/4 设(X,Y)有下面的概率密度函数: 那么可得: 此时,可证f(x,y)为PDF 如果分布被定义在一个非矩形区域,那么计算将会有点复杂.此处有一个例子,引用至DeGroot and Schervish(2002).假设(X,Y)有下面的密度函数: 请注意, 这里的关键是要注意积分得范围.我们选择一个变量,比如 x,然后让它在其取值范围内变化。然后,对于每个固定的 x 值,我们让 y 在其范围内变化,即 x^2 ≤ y ≤ 1。如果你查看下图,则可能会对你有所帮助 现在让我们来计算P(X>=Y),这个对应的集合为:A={(x,y);0<=x<=1,x^2<=y<=x}因此 如果(X,Y)满足联合分布,且其质量函数为 对于y的边缘质量函数(marginal mass function)被定义为: 假如 可得 对于连续随机变量,边缘密度函数(marginal density function)被定义为: 则对应的边缘分布函数,由 假定 令(X,Y)有如下的密度函数 因此,可得 有两个随机变量X和Y,若对于所有A和B,有 原则上,要检查X和Y是否独立,我们需要根据定义中的式子来检查所有的A,B子集.但幸运的是,我们有下面的结论可以使用,尽管这些结论是用连续的随机变量表述,但它也适用于离散随机变量 假设X和Y有联合PDF 设X,Y有下面的分布 那么 假如X,Y有下面的分布 那么X和Y不是独立的,因为 假定X和Y是独立的,并且有相同的密度函数,如下: 让我们来求 下面的结论有助于验证独立 假定X和Y的范围是一个矩形(可能是无界的),如果对于函数g和h(不一定是概率密度函数),满足 令X和Y有下面的密度函数: X和Y的范围是一个矩形 如果X和Y是离散的,那么我们可以计算在Y=y情况下的X的条件分布.具体来说 如果, 对于连续分布,我们使用相同的定义.解释的不同则为:在离散情况下条件概率质量函数,就是条件概率 对于连续的随机变量,条件概率密度函数(conditional probability density function)定义如下:假如 那么,概率则为: 假设X和Y,在单位正方形上有一个联合均匀分布(joint uniform distribution).因此在 从条件密度的定义可得: 在2.27例子中,可得 所以, 假如X服从 则Y的边缘密度函数为: 思考例子2.28中的密度函数,求 当X=x,y必须满足 现在求 令X=(X1,X2...Xn),这里的X1,X2..Xn都是随机变量(Random Variables),称X为随机向量(Random Vector).令 如果对于每一个A1,A2,...An,有 如果X1,X2,....Xn相互独立的,且有相同的累积分布函数(CDF)F,我们就说X1,X2,...Xn是独立同步分布(independent and identically distributed)写作: 如果F的密度函数为f,也可以写作 统计学理论和实践的大部分内容都以独立同分布(IID)的观测数据为基础,当我们讨论统计学时,我们将详细研究这种情况。 Multinomial (多项分布):二项分布的多维版本就称为多维分布.考虑从装有k个不同颜色的盒子中,抽取1个小球.这些小球上标有:"color1,color2....colork".令p=(p1,...pk),其中pj>=0,且 其中, 假如 Multivariate Normal(多维正态分布或者多元正态分布):一维正态分布有两个参数,μ和σ.在多维的版本中,μ是一个向量,σ则是一个矩阵Σ. 现在令 其中, 我们就说Z符合标准的多元正态分布,写作: 更一般的,如果向量X有下面的密度函数,则X是一个多维的正态分布向量,记作: 其中 因为Σ是对称,正定矩阵.因此存在一个矩阵 如果 假定将随机正态向量X分成X=(Xa,Xb)那么可以将μ写成μ=(μa,μb),Σ写成 设 假如X是CDF为 假如P(X=-1)=P(X=1)=1/4 ,P(X=0)=1/2.令Y=X^2.那么P(Y=0)=P(X=0)=1/2,P(Y=1)=P(X=1)+P(X=-1)=1/2.如下: Y的取值比X的取值少,这是因为这种转换不是一对一的. 而对于连续情况就比较复杂了,这儿有下面三个步骤去求 3. PDF就为CDF的导数: 令 因此 设 Y仅可取(0,9)之间的值,考虑两种情况:第一种, 0 对于第一种情况, 对于第二种情况, 对F求导得: 当r是严格的单调递增,或者单调递减,那么r有其反函数, 在某些情况下,我们对多个随机变量的转换感兴趣.例如,如果X和Y是给定的随机变量.我们可能像知道X/Y,X+Y,max{X,Y}的分布.令Z=r(X,Y)为我们感兴趣的函数.那么求 3. 然后对其求导; 设 (X1,X2)的联合密度函数为: 令 现在来到了困难的部分:求出 首先假设 在此种情况下, 再假设 对其求导,得PDF 本章完 未翻译:附录,课后作业 ![]()
![]()
![]() 和
和![]() 表示.PDF图像如下:
表示.PDF图像如下:![]()
![]() 和
和![]() .大多数的统计学教材,包括本书,都有一个
.大多数的统计学教材,包括本书,都有一个![]() 值表
值表2.17 例子
![]() ,求
,求![]() .解决思路是:
.解决思路是:![]() ,这个意味着,我们需要求出q,满足P(X
,这个意味着,我们需要求出q,满足P(X![]() .因此,
.因此,![]() 得q=1.1181
得q=1.1181![]()
![]()
![]() .如果概率密度函数满足如下,则称X满足参数为α和β的伽马分布(gamma distribution),写作:
.如果概率密度函数满足如下,则称X满足参数为α和β的伽马分布(gamma distribution),写作:![]()
![]()
![]() 是独立分布的,那么满足
是独立分布的,那么满足![]()
![]() :
:![]()
![]() :
:![]()
![]()
![]() distribution(卡方分布):如果f(x)满足如下,则成X为自由度p个自由度的卡方分布(χ^2 distribution),写作:
distribution(卡方分布):如果f(x)满足如下,则成X为自由度p个自由度的卡方分布(χ^2 distribution),写作:![]()
![]()
![]()
2.5 二维分布(Bivariate Distributions)
![]() ,从现在开始,将
,从现在开始,将![]() 写成
写成![]() .当需要更加复杂的式子时,将
.当需要更加复杂的式子时,将![]() 直接写成
直接写成![]()
2.18 例子
Y=0
Y=1
X=0
1/9
2/9
1/3
X=1
2/9
4/9
2/3
1/3
2/3
2.19 二维随机变量的PDF定义
![]() ,有
,有![]()
![]() 并且
并且![]() ,有
,有![]()
![]()
2.20 例子
2.21 例子
![]()
2.22 例子
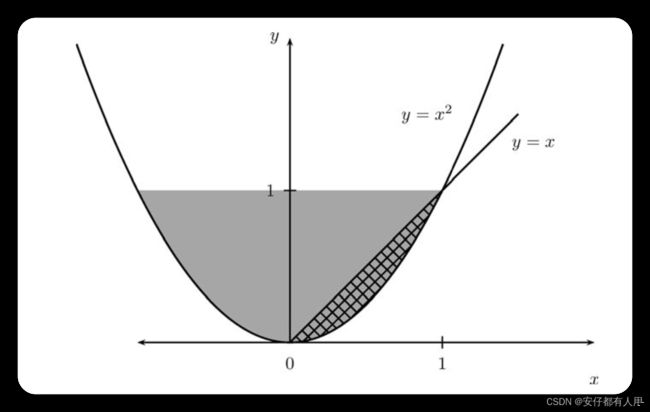
![]() .现在让我们来求c的值.
.现在让我们来求c的值.2.6 边缘分布(Marginal Distributions)
2.23 定义
![]() .那么对于x的边缘质量函数(marginal mass function)被定义为:
.那么对于x的边缘质量函数(marginal mass function)被定义为:![]()
2.24 例子
![]() 由下表给出.对于X的边缘分布,则是行的总和,对于Y的边缘分布则是列的总和
由下表给出.对于X的边缘分布,则是行的总和,对于Y的边缘分布则是列的总和
Y=0
Y=1
X=0
1/10
2/10
3/10
X=1
3/10
4/10
7/10
4/10
6/10
![]() ,
,![]()
2.25 定义
![]()
![]() 表示
表示2.26 例子
![]() ,那么
,那么![]()
2.27 例子
![]()
2.28 例子
![]()
2.7 独立随机变量 (Independent Random Variable)
2.29 定义
![]() ,那么我们就说X和Y独立.写作
,那么我们就说X和Y独立.写作![]() .反之,则称X和Y相关,写作,如下(贴图)
.反之,则称X和Y相关,写作,如下(贴图)
2.30 定理(Theorem)
![]() ,当且仅当
,当且仅当![]() 对于所有x和y成立时,那么
对于所有x和y成立时,那么![]()
2.31 例子
Y=0
Y=1
X=0
1/4
1/4
1/2
X=1
1/4
1/4
1/2
1/2
1/2
1
![]() ,且
,且![]() .X和Y是独立的,因为
.X和Y是独立的,因为![]() ,
,![]() ,
,![]() ,
,![]() .
.
Y=0
Y=1
X=0
1/2
0
1/2
X=1
0
1/2
1/2
1/2
1/2
1
![]() 但
但![]()
2.32 例子
![]() .使用独立性,那么联合密度函数就为:
.使用独立性,那么联合密度函数就为:2.33 定理
![]() ,那么X和Y是独立的.
,那么X和Y是独立的.2.34 例子
![]() ,还可以将f(x,y)写成f(x,y)=g(x)h(y).其中,
,还可以将f(x,y)写成f(x,y)=g(x)h(y).其中,![]() ,
,![]() .因此
.因此![]()
2.8 条件分布(Conditional Distribution)
![]() ,这使我们定义条件概率质量函数如下
,这使我们定义条件概率质量函数如下2.35 条件概率质量函数(conditional probability mass function)定义
![]() 条件概率质量函数定义如下:
条件概率质量函数定义如下:![]()
![]() .而对于连续情况下,就必须进行积分求得概率.
.而对于连续情况下,就必须进行积分求得概率.2.36 条件概率密度函数(conditional probability density function)定义
![]() ,
,![]()
![]()
2.37 例子
![]() 下,
下,![]() .在其他地方则为0.给定Y=y的情况下,X就是Uniform(0,1)分布.我们可以写作:
.在其他地方则为0.给定Y=y的情况下,X就是Uniform(0,1)分布.我们可以写作:![]()
![]() .这在某些情况下非常有用,如2.39 例子
.这在某些情况下非常有用,如2.39 例子2.38 例子
![]() .因此:
.因此:
2.39 例子
![]() .在获得X值之后,产生的Y服从
.在获得X值之后,产生的Y服从![]() .那么Y的边缘分布函数是什么?
.那么Y的边缘分布函数是什么?![]()
![]() ,其中
,其中![]()
2.40 例子
![]() .
.![]() .在前面,求出了
.在前面,求出了![]() .因此对于
.因此对于![]() ,则有:
,则有:![]()
![]()
2.9 多维分布和独立同步分布(Multivariate Distributions And IID)
![]() 是其PDF.可以定义他们的边缘分布,条件分布,其大多于二维的情况类似.
是其PDF.可以定义他们的边缘分布,条件分布,其大多于二维的情况类似.![]() ,则X1,X2...Xn是独立的.通过检查
,则X1,X2...Xn是独立的.通过检查![]() 即可.
即可.2.41 IID定义
![]() .
.![]() .我们也称X1,...Xn是来自于F的n个随机样本(random sample of size n from F)
.我们也称X1,...Xn是来自于F的n个随机样本(random sample of size n from F)2.10 两个重要的多维分布
![]() ,设pj是抽中小球颜色为j的概率.抽n次(有放回的独立抽样)且令X=(X1,X2..Xk)其中Xj表示颜色j出现的次数.因此
,设pj是抽中小球颜色为j的概率.抽n次(有放回的独立抽样)且令X=(X1,X2..Xk)其中Xj表示颜色j出现的次数.因此![]() .此时我们就说X满足Multinomial(n,p)分布,写作:
.此时我们就说X满足Multinomial(n,p)分布,写作:![]() .对应的概率函数为:
.对应的概率函数为:![]()
![]()
2.42 引理
![]() ,其中X=(X1,X2..Xk),p=(p1,p2...pk).Xj的边缘分布就是Binomial(n,pj)分布
,其中X=(X1,X2..Xk),p=(p1,p2...pk).Xj的边缘分布就是Binomial(n,pj)分布![]()
![]() 且相互独立.则Z的密度函数为:
且相互独立.则Z的密度函数为:
![]() ,其中,0表示有k个0元素的向量. 大写的I表示
,其中,0表示有k个0元素的向量. 大写的I表示![]() 的单位矩阵.
的单位矩阵.![]()
![]()
![]() 表示Σ的行列式.μ是一个长度为k的向量.Σ是一个
表示Σ的行列式.μ是一个长度为k的向量.Σ是一个![]() 对称的正定矩阵. 如果μ=0,Σ=I,则变成了标准多维正态分布
对称的正定矩阵. 如果μ=0,Σ=I,则变成了标准多维正态分布![]() ----称为Σ的平方根----满足下面的性质:
----称为Σ的平方根----满足下面的性质:
![]() 也是对称的
也是对称的![]()
![]() ,其中
,其中![]()
2.43 定理
![]() 并且
并且![]() ,那么
,那么![]() 反之,如果
反之,如果![]() 那么
那么![]()
![]()
2.44 定理
![]() ,那么
,那么
![]()
![]()
![]()
![]()
2.11 随机变量的转换
![]() ,PDF为
,PDF为![]() 的随机变量.令
的随机变量.令![]() 是关于X的函数.例如
是关于X的函数.例如![]() ,或者
,或者![]() .我们称
.我们称![]() 为X的转换.那么我们怎么计算Y的PDF和CDF呢?在离散情况下,答案非常容易.Y的质量函数如下:
为X的转换.那么我们怎么计算Y的PDF和CDF呢?在离散情况下,答案非常容易.Y的质量函数如下:2.45 例子
x
![]()
-1
1/4
0
1/2
1
1/4
y
![]()
0
1/2
1
1/2
![]()
![]()
![]()
![]()
2.46 例子
![]() ,x>0.因此
,x>0.因此![]() .设
.设![]() .那么
.那么![]() 那么
那么![]()
2.47 例子
![]() ,求
,求![]() 的PDF.X的密度函数为:
的PDF.X的密度函数为:![]() .
.![]()
![]() ,
,![]()
![]() ,在这种情况密度函数可以表示为:
,在这种情况密度函数可以表示为:![]()
2.12 多个随机变量的转换
![]() 的步骤和前面的类似:
的步骤和前面的类似:
![]()
![]()
2.48 例子
![]() 且独立.求
且独立.求![]() 的密度函数
的密度函数![]() ,得:
,得:![]()
![]() .
.![]() ,那么
,那么![]() 就是(0,0),(y,0),(0,y)围成的三角形.如下图
就是(0,0),(y,0),(0,y)围成的三角形.如下图![]() 是三角形的面积为
是三角形的面积为![]()
![]() ,那么
,那么![]() 就是除了(1, y - 1), (1, 1), (y - 1,1)围成三角形以外的所有区域.这部分面积为
就是除了(1, y - 1), (1, 1), (y - 1,1)围成三角形以外的所有区域.这部分面积为![]() .因此
.因此